Abstract
With Yonatan Aumann, Department of Computer Science, Bar Ilan University, Ramat Gan, Israel.
Game theory is not about games. It is a scientific field that uses logic to understand how decisions should be made, taking into account the choices of others. Despite its name, it deals with serious real-life situations like business, politics or even war. This article explains what game theory is about, and how it can be used in many real-world settings. I will explain how game theory uncovers the roots of cooperation, and why its study is important for reducing hostility. We will conclude with an elegant game theory method which you can apply in your everyday life.
Professor Robert Aumann won the Nobel Prize in Economics in 2005, jointly with Prof. Thomas Schelling, for having enhanced our understanding of conflict and cooperation through game theory analysis.
Early Bus or Late Bus?
I study the scientific field called “game theory.” Game theory is really not about games. To explain what game theory is about, let us start with some examples.
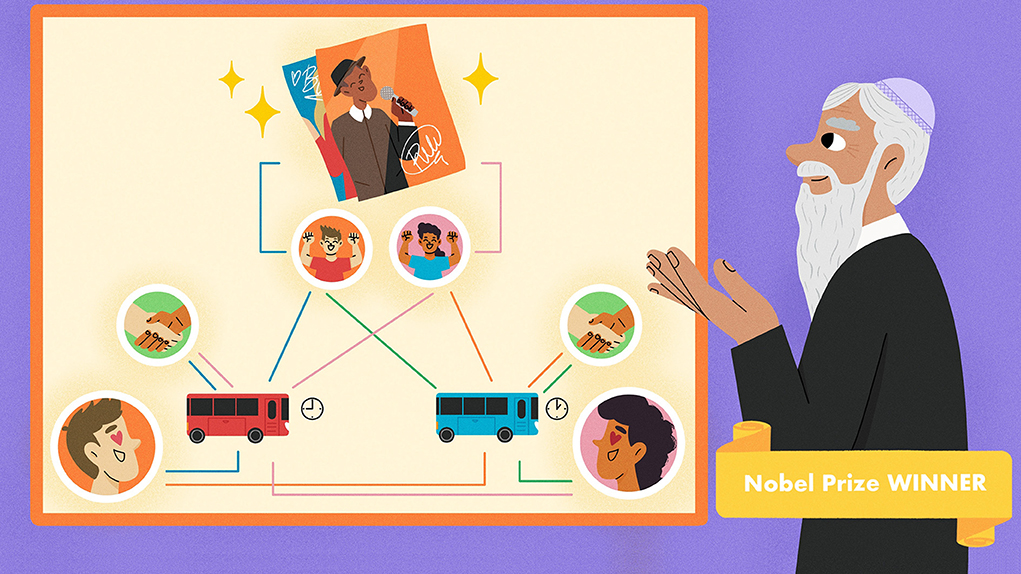
Suppose your hobby is collecting celebrity autographs. One day, you get the following message from Chris, a legendary autograph collector from a nearby town: “At the age of 85, I have decided to end my autograph-collecting hobby. I will give away my entire collection to whoever comes to my house first, starting at midnight tonight. If several people arrive at the same time, I will split the collection equally among them all.”
You know that no one in Chris’s town is interested in autographs, but there is another collector, Beth, who lives in your town. Two buses run from your town to Chris’s, one leaving at 5 AM and one at 9 AM. Which bus should you ride?
If you think about it, you should most definitely ride the 5 AM bus. The reasoning is as follows.
- If Beth rides the 9 AM bus, then you should ride the 5 AM bus—thus winning the entire collection.
- If, on the other hand, Beth decides to ride the 5 AM bus, then you should do the same, in order to get at least half the collection (with the 9 AM bus you would end up with nothing).
So, regardless of what Beth does, you should ride the 5 AM bus.
But the same reasoning is also true for Beth. So you both meet, red eyed, on the 5 AM bus, on the way to splitting the collection. Evidently, you would both be better off if both of you took the 9 AM bus—you would get more sleep, and the same number of autographs. But that desirable outcome is not possible! If each of you behaves rationally—that is, does what is best for him/her—then riding the 5 AM bus and splitting the collection is the only reasonable thing to do.
Now, suppose there is yet another bus, leaving at 2 AM. Which bus should you take? Unlike in the previous case, your best choice depends on what Beth does:
a) If Beth takes the 9 AM bus, then your best choice is to take the 5 AM bus.
b) If Beth takes either the 5 or 2 AM bus, then your best choice is to take the 2 AM bus.
Is it reasonable to suppose that Beth will take the 9 AM bus? Well, you know that Beth is a clever girl, so you expect her to follow the same reasoning as yours. So, she will not take the 9 AM bus—just as you would not. So, Case (b) holds, and your best choice is the 2 AM bus. The same is true for Beth. So again, you and Beth meet sleepless on the 2 AM bus, getting the exact same number of autographs you would have gotten if you had both taken the 9 AM bus!
In this example, did you notice how logical reasoning was used to figure out the best decision? This type of reasoning is what game theory is all about. Game theory is the logical analysis of decision making, specifically in situations involving multiple parties with possibly conflicting interests. Game theory uses logical reasoning to analyze such situations.
Another Example of Logical Reasoning
Here is another example. Suppose you and Beth play a game with the following rules: First, each of you secretly writes either the number 1 or the number 2 on a piece of paper. Then, you both reveal your choices. If Beth wrote 1, then she pays you the amount that you wrote (in dollars). If Beth wrote 2, then you pay her the amount that you wrote. What should you do? Here is a table of the possible choices and outcomes (Table 1):
| Beth | |||
|---|---|---|---|
| 1 | 2 | ||
| You | 1 | Beth pays you 1 | You pay Beth 1 |
| 2 | Beth pays you 2 | You pay Beth 2 |
- Table 1 - Logical reasoning game rules.
Choosing 2 is better if Beth chooses 1, while choosing 1 is better if Beth chooses 2. So, in order to determine your best move, you must try to figure out what Beth will do—but this is easy. For Beth, choosing 2 is clearly the better choice, regardless of what you do. If Beth is smart, she will always play 2, which means you should play 1.
As with the bus example, logical reasoning was used to analyze the situation and determine the best play. We employed “game theory”—the logical analysis of decision making in situations involving multiple parties. Importantly, game theory analyzes such situations from a purely logical perspective, without involving emotions and psychology. It tries to determine the most logical decision.
If Not Games, Then What?
The name “game theory” is misleading. Game theory is mostly not about games (although it can also be applied to games). Rather, game theory considers any interaction among multiple parties with conflicting interests, and uses logical reasoning (and mathematics) to analyze such interactions.
Game theory can be applied to situations much more serious than getting an autograph collection, such as business, politics, and even war.
Consider two neighboring countries that are hostile to each other. We will call them Astan and Beestan. Both countries keep armies along the shared border. The armies are stationed next to each other, on opposite sides of the border. Come night, soldiers of both armies enter their barracks, hoping for a good night’s sleep, except for a couple of soldiers standing guard. But now, the Astan commander says to his deputy, “I have an idea. Since Beestan’s army is going to sleep, this is our chance to attack them. Using all our troops, we can easily overcome their guards, and surprise attack the others in their sleep. Wake up all our soldiers. We are heading to the border!”
The deputy, wanting to sleep, replies, “Sir, but what if Beestan’s army does not go to sleep? Then we will not be able to defeat them.” To which the commander replies, “If that is the case, we surely need to head to the border, or else they will attack us!” With this fully rational argument, Astan’s entire army heads to the border, ready for battle.
But the exact same rational argument is also true for Beestan’s unit. So, they also head to the border, where the two units meet—for an unavoidable brutal clash. What a waste!
Sadly, the same logic seems to hold every night… so are the two units destined to endless clashes, night after night? Does game theory tell us that endless fighting is the only rational behavior?
Fortunately, the answer is no. In fact, advanced game theory analysis tells us the opposite: in such situations, logical reasoning leads to increased cooperation, not confrontation.
How can that be? Is there a flaw in the commander’s logic? Yes and no. The commander’s logic is indeed irrefutable if each night is considered on its own. But, when considering the repeated nature of the conflict, night after night, the logic changes. How so?
Consider again the conversation between the commander and his deputy. The commander wants to attack, but now the deputy says, “Sir, yesterday I was walking along the border and spotted the deputy of Beestan’s army. He shouted over the fence that they plan on going to sleep tonight; and he warned me that if we attack them in their sleep, they will retaliate and attack us every night from now on! I shouted back that the same is true for us.”
Is attacking tonight still the most logical move? Probably not. Even though an attack would give the attacker some short-term advantage, this advantage will be overshadowed by the overall loss created by fruitless battles that will then take place night after night. This is true for both sides! So, both units choose not to attack and to enjoy a good night’s sleep. The same thing happens the night after, and the night after that…
You can see that repeated interaction completely changes the situation! While confrontation was the logical move in the one-time case, cooperation is the logical behavior when interactions will happen again and again. Game theory teaches us that cooperation is frequently the most logical behavior in repeated interactions, even between opposing and hostile parties! This means that, according to game theory, cooperation is frequently the best possible action—even if all that you care about is your own good.
Making the World a Better Place
Why am I stressing this point? Because that is what I got my Nobel prize for!
In the words of the prize committee:
Robert Aumann was awarded the Prize in Economic Sciences for his theory of repeated games, which enhances our understanding of the prerequisites for cooperation.
So, the Nobel prize committee thinks that this idea—that cooperation is a result of repeated interaction—is sufficiently important to deserve a Nobel prize!
If you think about it, the idea itself is actually quite simple; If you will meet someone again, you may be better off cooperating. But although it is simple, it is extremely important. Our world is full of hostility, wars, and conflicts. We all want this situation to change. How can we bring about such change? Some people work or volunteer in peace organizations, while others use their political or financial power. All these are worthy and important undertakings; but as a scientist, I believe that a systematic and scientific study of the topic is no less important. I believe that understanding the causes of conflict and cooperation is a necessary first step toward promoting peace. You cannot build an airplane without understanding the laws of physics, and you cannot find a cure for cancer without understanding how cancer cells function. Similarly, I believe that you cannot promote cooperation without understanding its true sources; and you cannot promote peace if you do not understand its true roots—as well as those of war. Understanding why people fight or cooperate and what makes nations go to war or live in peace is necessary if we wish to try to change human behavior for the better. Game theory provides us with such an understanding. Therefore, I see my study of game theory as my small contribution to improving the world.
I will end this article with a clever and practical game theory idea that you can use in your everyday life for reducing envy and conflict. Suppose that your mother got you and your brother a tasty doughnut: vanilla-flavored dough covered with chocolate and candies. Unfortunately, she only got one—so you will need to share. What is the best way to split the doughnut? One solution is for your mother to cut the doughnut in half and give one piece to each of you. But, as your mother probably knows all too well, this could easily result in one of you being unhappy and envious of the other. Regardless of how fairly your mother tries to split the doughnut, one of you will probably think that their piece is smaller, has less chocolate or candies, or has some other flaw. Letting you or your sibling split the doughnut is probably not a good idea either! So, how should the doughnut be split?
Game theory has an elegant solution. It suggests using the following procedure (Figure 1):
- Your brother cuts the doughnut into two pieces, in any way he sees fit.
- You choose one of the pieces for yourself.
- Your brother gets the remaining piece.

- Figure 1 - A clever procedure for splitting a treat.
- (A) Suppose your mother buys you and your brother a tasty treat. How should she split it between you and your brother so that both of you will be satisfied? (B) Game theory suggests that, first, your brother cuts the treat into two pieces. (C) Next, you choose which piece you want to eat and then your brother gets the other piece.
Here is why with this procedure, neither you nor your brother have any cause for complaint or grumble.
You surely cannot complain, because you got to choose your piece. But what about your brother? Since you get to choose, is he not getting the lesser piece? The answer is no. Remember that he gets to cut the doughnut however he wants. When doing so, his reasoning should be as follows: “After I cut the doughnut in two, my sibling gets to choose their piece. If I create two uneven pieces, then my sibling will take the better piece, and I will get the lesser one. So it is best for me to split the doughnut into two exactly even parts. This guarantees that I get my fair share.”
In this way, both you and your brother get equally desirable shares, and neither of you can grumble! Is that not a clever solution? I frequently used it with my kids.
Conflict of Interest
The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
This article was written with Yonatan Aumann, Department of Computer Science, Bar Ilan University, Ramat Gan, Israel. Noa Segev conducted the interview that served as the basis for the first draft of this article. Alex Bernstein provided the figure.