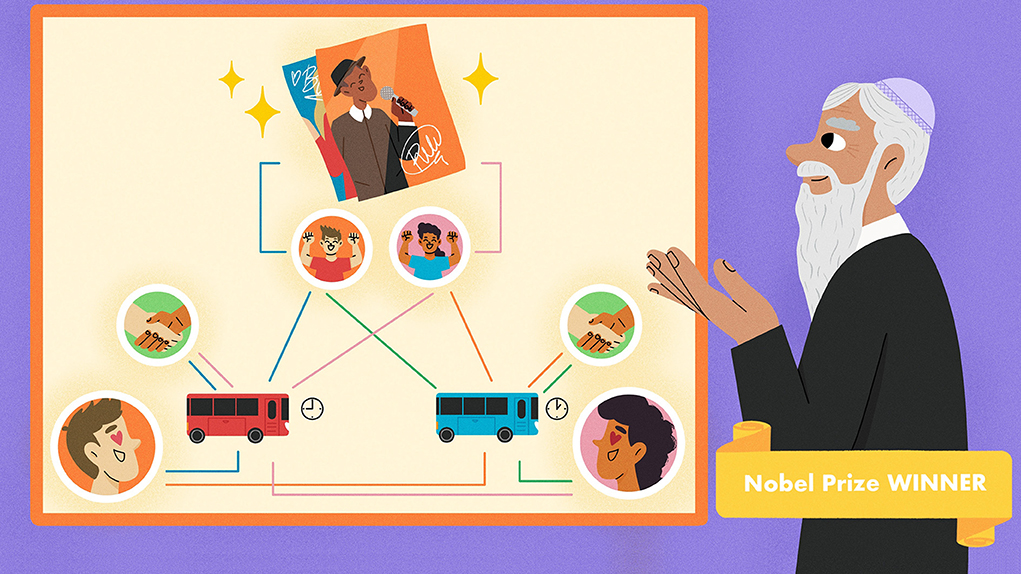
פרופסור רוברט (ישראל) אוּמָן זכה בפרס נובל לכלכלה לשנת 2005, עם פרופ’ תומאס שלינג (Thomas Schelling), עבור העמקת ההבנה בנושאי עימות ושיתוף פעולה באמצעות תורת המשחקים.

האם לנסוע באוטובוס המוקדם או המאוחר?

אני חוקר את תחום המדע שנקרא ”תורת המִשחקים”. למרות השם, תורת המשחקים אינה באמת עוסקת במִשחקים. כדי להסביר במה היא כן עוסקת, אציג כמה דוגמאות.

נניח שהתחביב שלכם הוא לאסוף חתימות של אנשים מפורסמים. יום אחד קיבלת הודעה מכריס, אספן חתימות אגדִי מעיר סמוכה לעיר המגורים שלך: ”הגעתי לגיל 85 ואני פורש מאספנות החתימות. החלטתי לתת את האוסף שלי למי שיגיע ראשון לביתי הלילה החֵל מחצות. אם כמה אנשים יגיעו באותו הזמן, אחלק את האוסף שווה בשווה ביניהם.”

ידוע לך שאף אחד בעיר של כריס אינו מעוניין בחתימות, אבל יש אספנית אחרת, בת’, שגרה בעיר שלך. יש שני אוטובוסים הנוסעים מהעיר שלך אל כריס: אחד יוצא ב-5 בבוקר והאחר ב-9 בבוקר. באיזה אוטובוס כדאי לך לנסוע?

ודאי שכדאי לך לנסוע באוטובוס שיוצא ב-5 בבוקר משתי סיבות:

• אם בת’ תיסע באוטובוס שיוצא ב-9 בבוקר, אז כדאי לך לנסוע באוטובוס שיוצא ב-5 בבוקר – ולזכות בכל האוסף.
• לעומת זאת, אם בת’ תחליט לנסוע באוטובוס שיוצא ב-5 בבוקר, גם אז כדאי לך לנסוע בו, כדי לזכות לפחות במחצית האוסף (כי אם בחרת לנסוע באוטובוס שיוצא ב-9 לא יישאר לך כלום).

לכן, ללא קשר למה שבת’ עושה, כדאי לך לנסוע באוטובוס שיוצא ב-5 בבוקר.

עם זאת, אלה גם השיקולים של בת’, ולכן שניכם נפגשים, עיניכם טרוטות, באוטובוס שיוצא ב-5 בבוקר, כשכל אחד מכם יקבל מחצית מהאוסף. ברור שהיה עדיף לוּ שניכם הייתם נוסעים באוטובוס שיוצא ב-9 בבוקר – הייתם ישנים יותר, וגם הייתם מקבלים אותו מספר חתימות. אבל התוצאה הרצויה הזו אינה אפשרית! כי אם כל אחד מכם מתנהג בצורה רציונלית – כלומר עושה מה שטוב עבורו – אז הדבר ההגיוני היחיד הוא לנסוע באוטובוס שיוצא ב-5 בבוקר ולהתחלק באוסף.

עכשיו, נניח שיש אוטובוס נוסף מהעיר שלך לעיר של כריס שיוצא ב-2 לפנות בוקר. באיזה אוטובוס כדאי לך לנסוע? שלא כמו במקרה הקודם, האפשרות הטובה ביותר עבורך תלויה במה שבת’ עושה:

א אם בת’ נוסעת באוטובוס שיוצא ב-9 בבוקר, עדיף לך לנסוע באוטובוס שיוצא ב-5 בבוקר.

ב אם בת’ נוסעת באוטובוס שיוצא ב-5 בבוקר או בזה שיוצא ב-2 לפנות בוקר, אזי האפשרות הטובה ביותר שלך היא לנסוע באוטובוס שיוצא ב-2 לפנות בוקר.

האם סביר להניח שבת’ תיסע באוטובוס שיוצא ב-9 בבוקר? ובכן, אתם יודעים שבת’ היא בחורה חכמה, אז אתם מצפים ממנה לחשוב על נימוקים זהים לשלך, ולכן היא לא תיסע באוטובוס שיוצא ב-9 - בדיוק כפי שאתם לא הייתם נוסעים בו. אז, מקרה (ב) מתקיים, והאפשרות הטובה ביותר עבורכם היא לנסוע באוטובוס שיוצא ב-2 לפנות בוקר. הדבר נכון גם לגבי בת’. אז שוב, שניכם נפגשים באוטובוס, ישנוניים, בשעה 2 לפנות בוקר, ושניכם מקבלים בדיוק את אותו המספר של חתימות שהייתם מקבלים אם שניכם הייתם נוסעים באוטובוס שיוצא ב-9!

האם שמתם לב כיצד בדוגמה זו נעשה שימוש בהנמקה הגיונית (לוגית) כדי להבין מהי ההחלטה הטובה ביותר? תורת המשחקים עוסקת בסוג זה של חשיבה – היא משמשת לניתוח לוגי של מצבים כדי לקבל החלטות, במיוחד כאשר לצדדים המעורבים יש אינטרסים מנוגדים. בתורת המשחקים אנו משתמשים בנימוקים לוגיים כדי לנתח מצבים מסוג זה.

דוגמה נוספת להנמקה לוגית

נניח שבת’ ואתם משַחקים משחק שאלו הם כלליו: ראשית, כל אחד מכם כותב על פיסת נייר בסתר את המספר 1 או את המספר 2. לאחר מכן, שניכם חושפים את הבחירות שלכם. אם בת’ כתבה 1, אז היא משלמת לך את הסכום שכתבת (בשקלים). אם בת’ כתבה 2, אז אתם משלמים לה את הסכום שכתבתם. מה עליכם לעשות? להלן טבלה של האפשרויות והתוצאות האפשריות (טבלה 1):

בת'
אתם		1	2
	1	1 בת' משלמת לי	1 אתם משלמים לבת'
	2	2 בת' משלמת לי	2 אתם משלמים לבת'

אםבת’ בוחרת ב-1, עדיף לכם לבחור ב-2, בעוד שאם בת’ בוחרת ב-2, עדיף לכם לבחור ב-1. לכן, כדי לקבוע את המהלך הטוב ביותר שלכם, עליכם לנסות להבין מה בת’ תעשה – אבל זה קל. עבור בת’, 2 היא ללא ספק הבחירה הטובה יותר, ללא קשר למה שאתם עושים. אם בת’ חכמה, היא תמיד תבחר ב-2, מה שאומר שאתם צריכים לבחור ב-1.

כמו בדוגמה של האוטובוס, עשינו שימוש בהנמקה לוגית כדי לנתח את המצב ולקבוע את המהלך הטוב ביותר. לשם כך, השתמשנו ב”תורת המשחקים” – ניתוח לוגי של קבלת החלטות במצבים שבהם מעורבים מספר צדדים. חשוב לציין שתורת המשחקים מנתחת מצבים כאלה מנקודת מבט לוגית גרידא, בלי לערב רגשות ופסיכולוגיה. היא מנסה לקבוע מהי ההחלטה ההגיונית ביותר.

אם לא מִשחקים, מה כן?

השם ”תורת המשחקים” מטעה, משום שלרוב תיאוריה זו אינה עוסקת במשחקים (אם כי אפשר ליישם אותה גם במשחקים). תורת המשחקים בוחנת כל אינטראקציה בין מספר צדדים בעלי אינטרסים מנוגדים, ומשתמשת בהנמקה לוגית (ובמתמטיקה) כדי לנתח אינטראקציות כאלה.

אפשר ליישם את תורת המשחקים במצבים חשובים יותר מקבלת אוסף חתימות, כמו בתחומים של עסקים, פוליטיקה ואפילו מלחמה.

נניח ששתי המדינות השכנות א’-סטאן וב’-סטאן עוינות זו לזו. לכן הצבאות של שתי המדינות נמצאים פרוסים זה מול זה משני צידֵי הגבול המשותף. עם רדת הלילה החיילים משני הצבאות נכנסים לצריפים שלהם, בתקווה לשנת לילה טובה, מלבד זוג חיילים שעומדים על המשמר. עכשיו מפקד א’-סטאן אומר לסגנו, ”אני מציע שכיוון שהצבא של ב’-סטאן לקראת שינה, זאת ההזדמנות שלנו לתקוף אותם. אם כל החיילים שלנו יילחמו, נוכל בקלות להתגבר על השומרים שלהם, ולתקוף במפתיע את האחרים בשנתם. תעירו את כל החיילים שלנו – אנחנו מסתערים!”.

הסגן, שרוצה לישון, עונה: ”המפקד, אבל מה אם הצבא של ב’-סטאן לא ישֵן עכשיו? במקרה כזה לא נצליח להביס אותם.” לכך המפקד עונה: ”אם זה המצב, ודאי שעלינו להתייצב בגבול, ולא – הם יתקיפו אותנו!” חמושים בטיעון ההגיוני הזה, כל צבא א’-סטאן מתקדם לעֵבר הגבול נכון לקרב.

עם זאת, הטיעון ההגיוני הזה בדיוק נכון גם לגבי היחידה של ב’-סטאן, אז גם הם הולכים לכיוון הגבול, ושם שתי היחידות נפגשות בהתנגחות אכזרית ובלתי נמנעת. איזה בזבוז!

למרבה הצער, נראה שאותו היגיון מתקיים בכל לילה... אז האם נגזר על שתי היחידות להתנגח בלי סוף, לילה אחר לילה? האם תורת המִשחקים אומרת לנו שלחימה אין-סופית היא ההתנהגות הרציונלית היחידה?

למרבה המזל, התשובה היא לא. למעשה, ניתוח מתקדם של תורת המִשחקים אומר לנו את ההפך: במצבים כאלה חשיבה לוגית מובילה לשיתוף פעולה מוגבר, ולא לעימות.

איך זה ייתכן? האם יש פגם בלוגיקה של המפקד? כן ולא. ההיגיון של המפקד אכן בלתי ניתן להפרכה אם כל לילה נחשב בפני עצמו, אבל כאשר מתחשבים באופי החזרתי של הסכסוך, לילה אחר לילה, ההיגיון משתנה. איך זה מתרחש?

הבה נחזור לשיחה שבין המפקד לבין סגנו. המפקד רוצה לתקוף, אבל עכשיו הסגן אומר לו: ”המפקד, אתמול הלכתי לאורך הגבול וזיהיתי את סגן המפקד של צבא ב’-סטאן. הוא צעק מעל הגדר שהם מתכננים לישון הלילה, והוא הזהיר אותי שאם נתקוף אותם בשנתם, הם ינקמו בנו ויתקפו אותנו כל לילה מעתה ואילך! צעקתי חזרה שאותו הדבר נכון לגבינו”.

האם לתקוף הערב עדיין יהיה הדבר ההגיוני ביותר לעשות? כנראה שלא. למרות שההתקפה תעניק לצבא התוקף יתרון לטווח קצר, יתרון זה יתגמד ליד ההפסד הכולל שייווצר מקרבות עקרים שיתרחשו אז לילה אחר לילה. זה נכון לשני הצדדים! לכן, שתי היחידות בוחרות שלא לתקוף, וליהנות משנת לילה טובה. אותו הדבר קורה בלילה שלאחר מכן, ובזה שאחריו...

כך נוכל לראות שאינטראקציה חוזרת ונשנית משנה לחלוטין את המצב! בעוד שעימות היה המהלך ההגיוני במקרה החד-פעמי, כאשר אינטראקציות מתרחשות שוב ושוב, שיתוף פעולה הוא ההתנהגות ההגיונית. תורת המִשחקים מלמדת אותנו ששיתוף פעולה הוא לרוב ההתנהגות ההגיונית ביותר באינטראקציות חוזרות ונשנות, אפילו בין צדדים בעלי עניינים מנוגדים ואפילו עוינים! כלומר, לפי תורת המִשחקים שיתוף פעולה הוא לרוב הפעולה הטובה ביותר האפשרית – גם אם כל מה שמעניין אתכם הוא טובתכם האישית.

הופכים את העולם למקום טוב יותר

מדוע אני מדגיש את הנקודה הזו? כי בזכותה קיבלתי את פרס הנובל!

ועדת הפרס ניסחה זאת כך:

”רוברט אוּמָן זכה בפרס נובל למדעי הכלכלה עבור התיאוריה שלו בנוגע לחזרתיות במִשחקים, המסייעת לנו להבין טוב יותר את התנאים המוקדמים לשיתוף פעולה”.

ועדת פרס נובל חשבה שהרעיון הזה – ששיתוף פעולה הוא תוצאה של אינטראקציה חוזרת ונשנית – חשוב מספיק כדי לקבל פרס נובל!

כשחושבים על זה לעומק, הרעיון הזה בעצם די פשוט: אם אתם פוגשים מישהו יותר מפעם אחת, אולי עדיף שתשתפו פעולה. עם זאת, למרות שהרעיון פשוט, יש בו חשיבות גדולה. העולם שלנו מלא בעוינות, במלחמות ובסכסוכים. כולנו רוצים שהמצב הזה ישתנה. איך אנחנו יכולים לגרום לשינוי כזה? יש אנשים שעובדים או מתנדבים בארגוני שלום, בעוד שאחרים משתמשים בכוחם הפוליטי או הפיננסי. כל היוזמות הללו ראויות וחשובות, וכמדען, אני מאמין שמחקר שיטתי ומדעי של הנושא חשוב לא פחות.

אני מאמין שהבנת הסיבות לסכסוכים ולשיתופי פעולה היא צעד הכרחי ראשון לקידום השלום. אי אפשר לבנות מטוס בלי להבין את חוקי הפיזיקה, ואי אפשר למצוא תרופה לסרטן בלי להבין איך תאים סרטניים מתפקדים. באופן דומה, אני מאמין שאי אפשר לקדם שיתופי פעולה בלי להבין את המקורות האמיתיים שלהם, ואי אפשר לקדם שלום אם לא מבינים את השורשים האמיתיים שלו, כמו גם את השורשים האמיתיים של המלחמה. אם ברצוננו לנסות לשנות את ההתנהגות האנושית לטובה, הכרחי להבין מדוע אנשים נלחמים או משתפים פעולה, ומה גורם לאומות לצאת למלחמה או לחיות בשלום. תורת המִשחקים מספקת לנו הבנה מסוג זה. לכן, חקר תורת המִשחקים היא בעיניי התרומה הקטנה שלי לשיפור העולם.

אסיים את המאמר ברעיון חכם ומעשי מתורת המִשחקים שתוכלו להשתמש בו בחיי היום-יום שלכם כדי להפחית קנאה ועימותים. נניח שאימא שלכם הביאה לך ולאחותך או לאחיך סופגנייה טעימה, מכוסה בשוקולד ובסוכריות. למרבה הצער, יש רק סופגנייה אחת ותצטרכו לחלוק אותה. מהי הדרך הטובה ביותר לחלק את הסופגנייה? אחד הפתרונות הוא שאימא שלכם תחלק את הסופגנייה לשניים, ותיתן חתיכה אחת לכל אחד מכם. עם זאת, כמו שאימא שלכם יודעת היטב, כנראה שאחד מכם לא יהיה מרוצה, כי גם אם אימא שלכם תחלק את הסופגנייה לחלקים שווים, אחד מכם ודאי יחשוב שהחתיכה שלו קטנה יותר, שיש עליה פחות שוקולד וסוכריות, או שהיא פחות טובה מהחתיכה השנייה. כנראה שגם אם אחד מכם יחלק את הסופגנייה, זה לא יפתור את הבעיה! אז איך אפשר לחלק את הסופגנייה ושכולם יהיו מרוצים?

תורת המִשחקים מציעה פתרון פשוט וחכם (איור 1):

1. אחותך או אחיך מחלקים את הסופגנייה לשני חלקים, לפי ראות עיניהם.
2. אתם בוחרים את אחת החתיכות לעצמכם.
3. אחותך או אחיך מקבלים את החתיכה הנותרת.

הנה הסיבות לכך שאם תבצעו את ההליך הזה, לאף אחד מכם לא תהיה סיבה להתלונן:

אתם ודאי לא יכולים להתלונן, כי אתם אלו שבחרתם את החתיכה. אבל מה עם אחותכם או אחיכם? כיוון שאתם אלו שבוחרים, האם אין הם מקבלים את החלק הקטן? התשובה היא: לא. זִכרו שהם חותכים את הסופגנייה איך שהם רוצים, ולכן הנימוק שלהם צריך להיות: ”לאחר שאני מחלקת או מחלק את הסופגנייה לשניים, אחותי או אחי הם אלו שיבחרו קודם את החתיכה. אם אחלק את הסופגנייה לחלקים שאינם שווים, אז אחותי או אחי יבחרו בחתיכה הטובה יותר, ואני אקבל את הקטנה. מסיבה זו, עדיף לי לחלק את הסופגנייה לשני חלקים שווים בדיוק. זה מבטיח לי שאני אקבל את מה שאני רוצה”.

כך כולכם יהיו מרוצים ממה שקיבלתם ואף אחד מכם לא יכול להתלונן! האין זה פתרון חכם? השתמשתי בו לעיתים קרובות עם הילדים שלי.

הצהרת ניגוד אינטרסים

המחברים מצהירים כל המחקר נערך בהעדר כי קשר מסחרי או פיננסי שיכול להתפרש כניגוד אינטרסים פוטנציאלי.

תודות

מאמר זה נכתב בשיתוף עם Yonatan Aumann מהמחלקה למדעי המחשב באוניברסיטת בר-אילן שברמת גן. נועה שגב ערכה את הריאיון שעליו התבססה הטיוטה הראשונית של מאמר זה. אלכס ברנשטיין ציירה את האיורים.

הצהרת כלי בינה מלאכותית

טקסט חלופי הנלווה לאיורים במאמר זה נוצר על ידי פרונטירז בסיוע כלי בינה מלאכותית, ונעשו מאמרצים על מנת להבטיח את דיוקו, כולל בדיקה על ידי כותבי המאמר כאשר הדבר התאפשר. אם ברצונכם לדווח על בעיה, אנו צרו איתנו קשר.