Abstract
Every day, we make many decisions that impact those around us, and we in turn are impacted by decisions that others make. This reciprocal impact makes it challenging to analyze situations that involve more than one participant. In the mathematical field of game theory, such situations are called games. When I participate in a game, I must guess what the other participants will do, so that I can choose the best course of action to cope with their decisions. The other participants are aware that I am trying to guess what they plan to do, and they in turn will adapt their actions based on what they guess my moves will be. Can game theory recommend players how to play to “win” or otherwise achieve their goals? This article will explain concepts related to game theory and help answer this question.
What Is A Game?
When we hear the word game, we think of football, Monopoly, chess, or computer games. Two features shared by the first three games and by some computer games are that more than one person participates in the game and that each player’s decisions impact the other participants.
In the mathematical field of game theory, any situation that shares these two features is called a game. According to this definition, we play games all day long, for example, in our relationships with family members, classmates, and teachers, and, of course in the real games we play. Game theory only studies games that involve more than one player. For example, the computer games Fortnite, League of Legends, and Call of Duty are considered games, but not the solitaire games Witcher and God of War.
The games we have mentioned are complex, and while playing, each player makes numerous decisions. To understand how to analyze games, let us look at a simple example—the shepherds’ game.
The Shepherds’ Game
Five shepherds live in a certain village, each taking care of a flock of sheep. At noon, the sheep are thirsty, and each shepherd leads his or her sheep to one of the village’s two wells: the northern well or the southern well. Each well is covered by a heavy stone that prevents sand and dirt from polluting the water, and five people are needed to remove the stone. To which well will each shepherd lead his or her flock?
The situation described here is a game: it has five participants—the five shepherds—and each player must make a decision—to go to the northern well or to go to the southern one. If all the shepherds lead their flocks to the same well, they will be able to remove the stone and water their flocks. If they do not all go to the same well, the sheep will remain thirsty. What should the shepherds do? It is clear that, to water the sheep, they must all choose the same well. This insight leads us to an important concept in game theory—equilibrium, which was invented by Nash [1].
The players’ behavior in the game is called an equilibrium if no player can profit by changing his or her behavior, provided the other participants do not change their behavior. In the shepherds’ game, one equilibrium is that all the shepherds meet at the northern well. If they all do so, together they can remove the stone and water their sheep. If one of the shepherds makes a different choice and decides to go to the southern well, the shepherd will find himself or herself alone there, will not be able to remove the stone and, most importantly, will not be able to water his or her sheep. A second equilibrium is that the five shepherds meet at the southern well.
There are additional equilibria in the shepherds’ game. For example, shepherds 1, 2, and 3 go to the northern well, and shepherds 4 and 5 go to the southern well. In this case, no well will be uncovered and so none of the shepherds will be able to water their sheep. Even if one of the shepherds changes his or her behavior and goes to the other well, there would still not be five people at the same well, and the shepherd would still not be able to water his or her flock. In other words, a change in the behavior of a single shepherd will not change the outcome and, consequently, this situation is also an equilibrium. While the first two equilibria described here are “good,” because the sheep quench their thirst, the third equilibrium is “bad,” because the sheep remain thirsty.
Braess’s Paradox
The concept of equilibrium enabled the German mathematician Dietrich Braess to explain an interesting phenomenon related to transportation. To describe it, let us look at the system of roads shown in Figure 1. Two highways connect Battle Creek and Detroit—a northern road that passes next to the city of Lansing and a southern road that passes next to city of Jackson. The travel time on each road section depends on the number of cars taking that road at any given moment. For example, the travel time from Battle Creek to Lansing is 20 min if fewer than 40 vehicles are traveling on the road per minute, and the travel time from Lansing to Detroit is 60 min if fewer than 40 vehicles are traveling on the road per minute. In any section of road where at least 40 vehicles are traveling, the travel time is extended by 20 min. For example, if 30 vehicles per minute are traveling on the northern route, the overall travel time from Battle Creek to Detroit is 80 min, and if 60 vehicles are traveling on this route per minute, the overall travel time is 120 min.
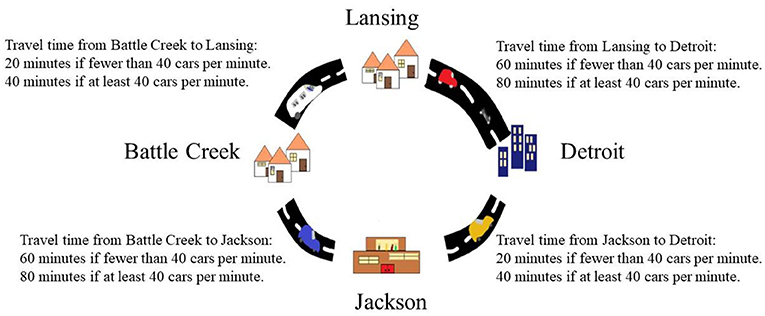
- Figure 1 - The roads connecting Battle Creek to Detroit and the driving times on each section of the road.
- When 60 vehicles per minute head from Battle Creek to Detroit, in equilibrium, between 21 and 39 go through Lansing and between 21 and 39 through Jackson, and the total driving time is 80 min (Image credit: Dor Solan).
Each driver can choose which route to take to Detroit and each driver’s goal is to minimize driving time. Let us look at a situation in which, early in the morning, 60 vehicles a minute set out from Battle Creek to Detroit. The situation described here is a game: it has 60 participants—the drivers setting out from Battle Creek to Detroit; and each player’s decision is the route they will take—the northern road or the southern road. As noted, the drivers wish to minimize driving time. What are the equilibria in this game? Each driver wants to take the route that has fewer than 40 drivers. For example, one equilibrium is when 35 drivers take the northern route and 25 take the southern route. Another equilibrium is when 29 drivers take the northern route and 31 take the southern route. In each equilibrium, the overall driving time from Battle Creek to Detroit is 80 min.
As part of an infrastructure upgrade project, a road 10 min long was constructed between Lansing and Jackson (Figure 2). It is easy to see that the two equilibria described earlier are no longer equilibria after the construction of the new road. Consider, for example, the equilibrium where 35 drivers take the northern route and 25 take the southern route. As previously, the overall driving time from Battle Creek to Detroit on the northern route is 80 min. However, if a driver chooses to travel from Battle Creek to Lansing on the northern route (travel time 20 min), then take the new road to Jackson (travel time 10 min), and from there drive to Detroit on the southern route (travel time 20 min, because there are now 26 cars on that section of the road), then the total travel time will be 50 min. In other words, by using the new road, the driver will save 30 min.
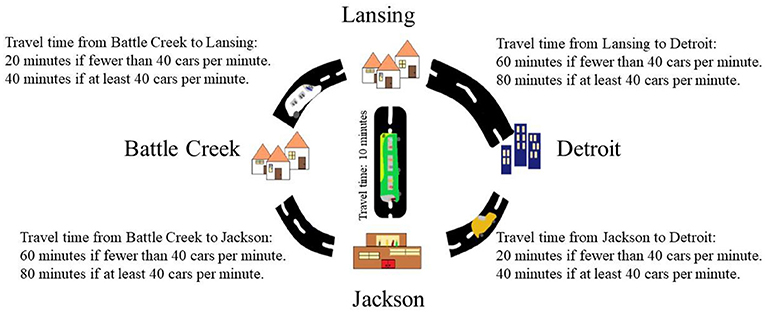
- Figure 2 - The road network after the construction of the new road.
- In equilibrium, all vehicles go from Battle Creek to Lansing, from there to Jackson, and from there to Detroit, and the total travel time is 90 min (Image credit: Dor Solan).
It turns out that, after the construction, the unique equilibrium is such that all drivers decide to go from Battle Creek to Lansing, from there to Jackson, and from there to Detroit (Figure 2). In this situation, the total travel time increases to 90–10 min more than before the new road was constructed. If one of the drivers chooses a different route—for example, the northern route—that driver’s travel time will increase to 100 min (40 min from Battle Creek to Lansing, and 60 min from Lansing to Detroit).
This result is surprising because, although the new road was built to shorten the travel time from Battle Creek to Detroit, it did exactly the opposite. This happens because, before the construction of the new road, fewer than 40 drivers used each of the two routes, but after its construction, all the drivers use sections of both the northern route and the southern route. In doing so, they jam both routes, increasing the overall travel time.
The phenomenon presented here actually happened in real life. In 1969, a new road was built in the German city of Stuttgart, but instead of improving the situation, it slowed down traffic to the city. The traffic returned to its previous situation only after the new road was closed. In another case in New York City, the city authority closed a number of road sections in 2009 and discovered that this led to an improvement in traffic flow. As a result, they turned these road sections into pedestrian malls.
Summary
The concept of equilibrium helps us analyze games. When the players’ behavior is an equilibrium, it is not beneficial for any of them to change their behavior, and consequently, this behavior is stable. This concept serves as the basis for modern economics, in which the assumption is that every member of the population wishes to maximize his or her objectives. This concept also serves as a cornerstone of networks in computer science, in which the assumption is that every user is trying to send and receive information as quickly as possible. Analyzing games and identifying their equilibria enables players to anticipate what will happen in the game, understand what they should do, and plan their next steps accordingly.
Glossary
Game: ↑ A situation with more than one participant, in which each participant has a certain goal and makes decisions, and these decisions impact the other participants.
Game Theory: ↑ An area of mathematics dealing with the analysis of games. Game theory is used as a decision-making tool in politics, economics, and other areas.
Equilibrium: ↑ Players’ behavior in which it is not in any player’s interest to be the only one to change their behavior, because that player will not benefit from the change.
Conflict of Interest
The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
[1] ↑ Nash, J. F. Jr. 1950. Equilibrium points in n-person games. Proc. Natl. Acad. Sci. U.S.A. 36:48–9.
