Abstract
When you think of fish, what comes to mind? Maybe you think of pet goldfish, movie characters like Dory or Nemo, or trout in a local river. One of the things that all these fish have in common is patterns in their skin. Nemo sports black and white stripes in his orange skin, and trout have spots. Even goldfish have a pattern—but it is just plain gold (and kinda boring). Why do some fish have stripes, others have spots, and others have plain patterns? It turns out that this is a tricky question, so scientists need tools from several subjects to answer it. In this paper, we use biology, math, and computer coding to help figure out how fish get different skin patterns.
What Are Fish Patterns Made of?
Many types of animals have skin patterns. Zebras have stripes and leopards have spots, but fish display all sorts of patterns—like stripes, spots, mazes, and plain patterns (Figure 1) [1]. Zebrafish (Figure 1G) are good for doing experiments with, so a lot of scientists like zebrafish best [2, 3]. As you might guess from the word “zebra” in their name, zebrafish usually have stripes.

- Figure 1 - Fish have all sorts of interesting skin patterns.
- (A) White stripes with orange; (B) purple and black stripes; (C) maze patterns; (D,E) spots; (F) plain; (G) zebrafish. Their patterns are made of pigment cells. (Image credits: (A) from Salis et al. [4] with permission from John Wiley & Sons, Copyright (2019) John Wiley & Sons A/S; (B) from Irion et al. [2] (licensed under CC BY-NC-ND 4.0); (C) from Frohnhöfer et al. [1] (CC-BY 3.0); (D) from Singh et al. [3] with permission from Elsevier, Copyright (2015) Elsevier Ltd.; (E) from Zouavman Le Zouave (CC BY-SA) via Wikimedia Commons; (F) from Bjwebb at English Wikipedia, Public domain, via Wikimedia Commons; (G) adapted and combined from Frohnhöfer et al. [1] (CC-BY 3.0) and Oregon State University (CC BY-SA) via Wikimedia Commons).
When we look at zebrafish from far away, we see black and yellow stripes. If we put a zebrafish under a microscope, however, we can see that the patterns are made up of tiny dots, or pigment cells. Pigment cells come in various sizes and colors—some are big and black (called melanophores) and others are small and yellow (called xanthophores). There are other colors of pigment cells too, and even humans have pigment cells in their skin.
Cells Follow Rules to Create Stripes
Okay, so fish patterns contain pigment cells. But what is really cool about pigment cells is that they actually have the job of making the stripes we see in fish [5]! You can watch a pattern form as a zebrafish is growing here. Do you see the black cells moving around in the movie? There are small yellow cells there too, but they are harder to see.
You can think of each pigment cell in zebrafish skin like it is a person moving in a group. You can move around in a room full of people, and pigment cells can move around in the skin, too. Black and yellow pigment cells move and act in specific ways (or follow rules) to create patterns. One of these rules is that yellow cells follow black cells. It is almost like they are playing tag, you’re it! You can see a black cell leading the way and a yellow cell following it in this movie [6]! Crazy!
How Do Scientists Study Fish Patterns?
While some of the rules for how pigment cells behave in zebrafish (like yellow cells following black cells [6]) are already known, many rules are a mystery. Scientists are working hard to discover those rules. Cells are tiny, and it is tough to see them and catch them interacting with each other in the skin. Zebrafish also take a few months to grow [3], so biologists must be patient with their experiments. This is where math and computer coding enter the picture. Math is all about patterns, rules, and puzzles, and it can be combined with biology to help figure out how cells behave [7, 8]. Mathematicians and biologists use different tools to study the same problems. Bringing their ideas together makes the mystery of how zebrafish get their stripes easier to solve.
While biologists study fish by looking into microscopes and doing experiments, mathematicians write down rules for how cells might behave [7, 8]. These rules and equations are called a mathematical model—a method of describing something in a mathematical way. It is important to remember that a model is a good guess, but it could be wrong. To test their rules, mathematicians use computer coding to simulate fish patterns. This is like growing fish on a computer! One good thing about simulating fish patterns is that it only takes a few minutes, not a few months…but we would not recommend trying to eat a simulated fish for dinner!:-)
Building a Mathematical Model of Zebrafish Stripes
Now we are ready to build a mathematical model of zebrafish patterns! Our first step is to describe fish skin as a checkerboard (Figure 2). Each square in the checkerboard can either be empty (white), have a yellow cell, or have a black cell. To simulate fish patterns, we need to tell the black and yellow cells where to appear on the checkerboard. In other words, we need to describe their rules of behavior. Biologists know that black cells mostly like to be near other black cells, and yellow cells like to have mostly yellow cells around them. We use this fact to build our mathematical model.
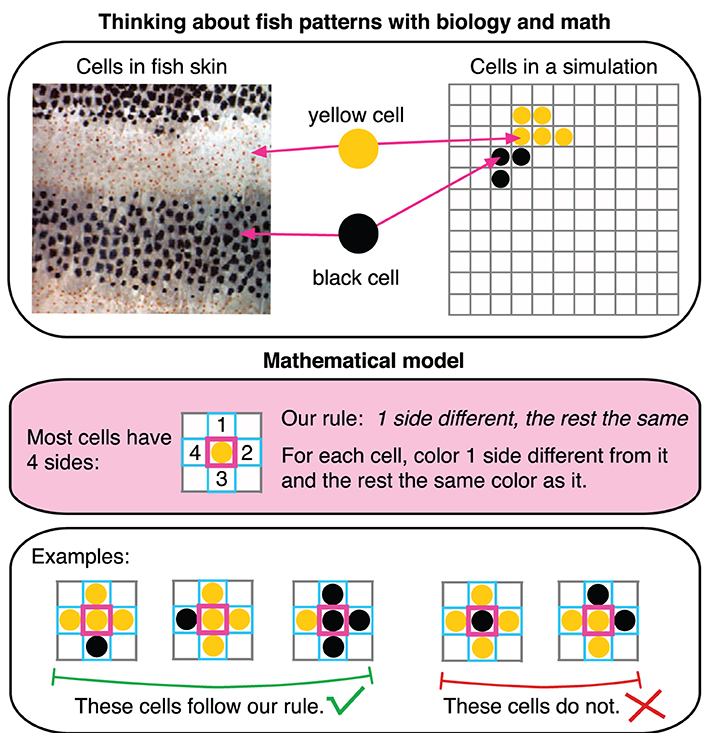
- Figure 2 - Cells follow rules to create patterns.
- To simulate patterns with a mathematical model on a computer, think of fish skin as a checkerboard [7]. Then pick a rule for what color cell goes in each square. Our rule is “one side different, the rest the same.” If you put your finger on a cell in the center (pink square), one of its neighbors (blue outline) should have a different color than the center cell, and the rest should be the same color as the center cell. “Cells in fish skin” image adapted from Frohnhöfer et al. [1] (CC-BY 3.0).
In Figure 2, each cell in the checkerboard has 4 sides (unless it is at a corner or an edge). Our rule is “one side different, the rest the same.” This means that, if you put your finger on a yellow cell, one of the cells that it touches should be black (different) and the other cells should be yellow (the same). To get some practice with this rule, try filling in the worksheet in Table 1 (instructions and answers are at the bottom of the table).
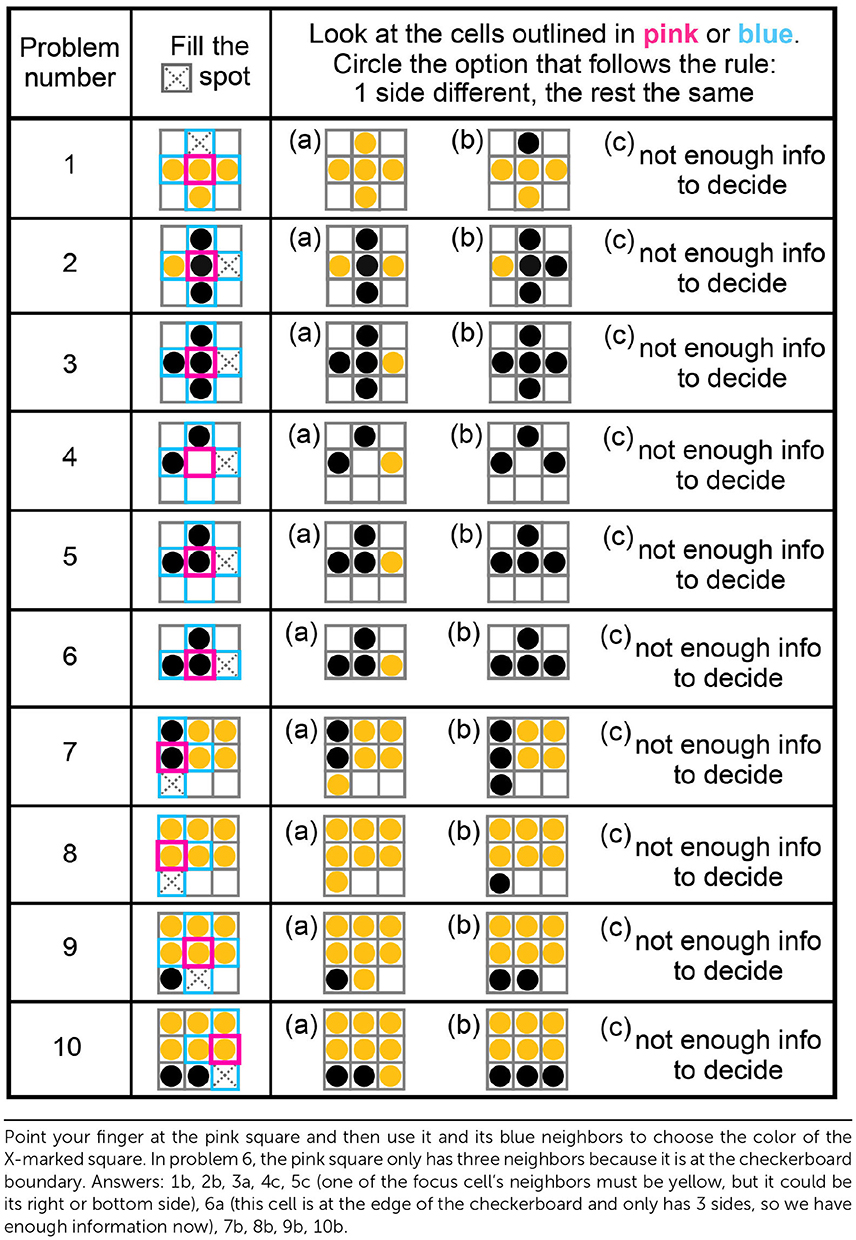
- Table 1 - Determine the option that follows the mathematical model in Figure 2.
Our model has only one rule, and the truth is that we are simplifying all the ways that zebrafish pigment cells actually behave. But that is okay! When mathematicians make models, they start with simple rules and then build more realistic ones. Simple models help scientists learn, and our model is a first step. If you would like to see more realistic models that mathematicians are working on now, check out [8].
Our Puzzle: Simulating Zebrafish Stripes
What pattern does the rule “one side different, the rest the same” create? You can try this out and build a fish pattern using Figure 3. Print this figure, cut out the black and yellow cells, and follow these steps:
- Step 1: Zebrafish have one yellow stripe when they are young, so start by putting two strips of yellow cells at the top of your fish checkerboard.
- Step 2: Fill out the rest of the checkerboard by following the rule “one side different, the rest the same.”
Start by filling out the squares at the top of the checkerboard and slowly move your finger down the fish from left to right. What pattern forms? By following the steps in Figure 3, you are doing the same steps by hand that a computer would do to simulate a fish pattern. We have used computer coding to create fish patterns—check out our website to simulate a fish yourself!1
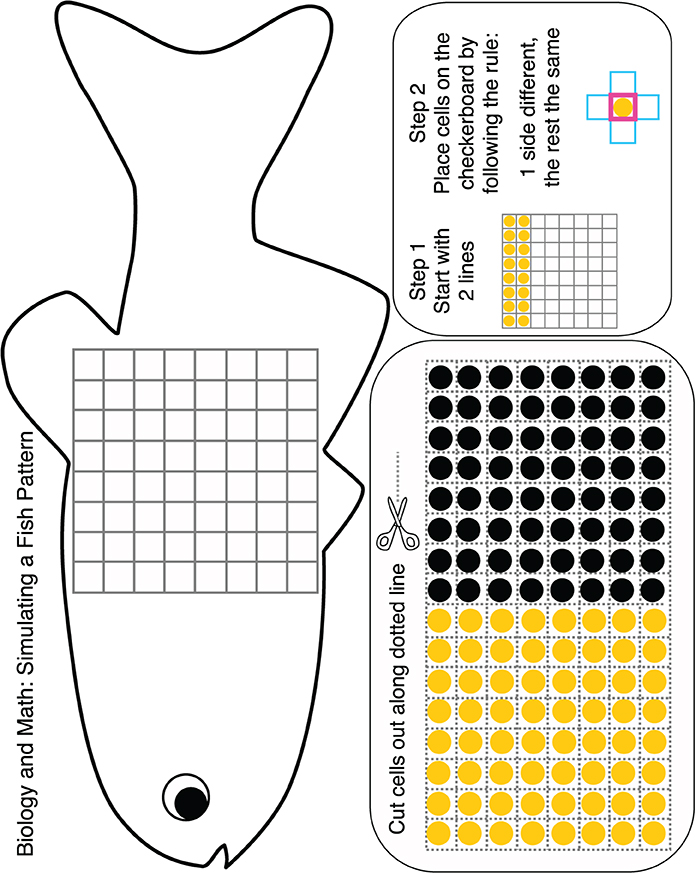
- Figure 3 - Use this image to create a fish pattern by combining biology and math.
- Fill in the checkerboard on the fish by following Steps 1 and 2. After you finish, print this page again. It is your turn to be the mathematician now—make up your own rules to discover other patterns that you can create! How would you change Step 2 to make a goldfish?
Why Is Studying Fish Patterns Important, Anyway?
Fish patterns might be nice to look at, but why do biologists and mathematicians study them? The answer has to do with mutant patterns, medicine, and humans.
What happens if the pigment cells do not follow their normal rules? This can happen if a fish has a mutation in its genes [2, 9]. Turns out Figure 1G is not the only picture of a zebrafish. Believe it or not, Figures 1C,D also show zebrafish, but they are mutants! Mutant zebrafish have different patterns because their cells follow different rules (Figures 1C,D). A fish’s genes specify these rules, so mutant genes lead to mutant rules and mutant patterns. Humans can also have mutations in their genes, which can sometimes cause disease. Zebrafish and humans may not look alike, but they actually have a lot of similar genes. That is why studying zebrafish is important—if we can figure out what rules cells follow to create normal and mutant patterns in fish, we might be able to better understand normal and unhealthy behavior of cells in humans down the line, too.
Now You Get to Be the Applied Mathematician!
Scientists are working hard to discover how black and yellow cells behave in normal zebrafish, and to figure out how these cells change their behavior in mutant fish [2, 9]. For mathematicians who study zebrafish, their job is to think about a fish pattern (like stripes) and then find the rules that can create that pattern [7, 8]. This is a puzzle. How would you change the rule “one side different, the rest the same” to create a plain yellow fish? What rules and starting points create diagonal stripes? By working on these questions, you are taking on the role of mathematician yourself! What fish patterns can you create with math?
Glossary
Pigment Cell: ↑ Cells are small units that all living things are made of (we are made of cells, and so is fish skin). Pigment cells are special cells that contain pigment (color).
Mathematical Model: ↑ Rules or equations that describe something in a mathematical way. In this paper, the rule “one side different, the rest the same” is part of our mathematical model.
Simulate: ↑ To imitate a real-world system on a computer. You can simulate fish patterns on our website with computer coding and a mathematical model, which provides directions to the computer: https://simulatingzebrafish.gitlab.io/zebrafish-outreach/.
Mutation: ↑ A change in an animal’s genes from the normal setting to something else. Zebrafish usually have stripes (Figure 1G), but mutant zebrafish (Figures 1C,D) have maze or spot patterns.
Genes: ↑ The biological instructions that an animal gets from their parents to specify their features (like stripe or spot patterns for a fish, or green or brown eyes for a person).
Acknowledgments
AV has been supported in part by the National Science Foundation under grant no. DMS-1764421 and by the Simons Foundation/SFARI under grant no. 597491-RWC. We are grateful to Jithin George, Katelyn Joy Leisman, Niall Mangan, and Sasha Shirman for helpful feedback on this manuscript, and BS thanks Sasha for providing suggestions on JavaScript. We also thank Domenico Bullara and Yannick De Decker for publishing their JavaScript code as part of [7], since it helped inspire the code that we developed for our website.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Additional Materials
https://simulatingzebrafish.gitlab.io/zebrafish-outreach/
Footnote
1. ↑When you finish your pattern, you may notice that the cells in the top and bottom row of the checkerboard do not follow the rule “one side different, the rest the same.” That is ok! Fish have a top and bottom where their body ends, and the cells there act a bit different.
References
[1] ↑ Frohnhöfer, H. G., Krauss, J., Maischein, H. M., and Nüsslein-Volhard, C. 2013. Iridophores and their interactions with other chromatophores are required for stripe formation in zebrafish. Development. 140:2997–3007. doi: 10.1242/dev.096719
[2] ↑ Irion, U., and Nüsslein-Volhard, C. 2019. The identification of genes involved in the evolution of color patterns in fish. Curr. Opin. Genet. Dev. 57:31–8. doi: 10.1016/j.gde.2019.07.002
[3] ↑ Singh, A. P., and Nüsslein-Volhard, C. 2015. Zebrafish stripes as a model for vertebrate colour pattern formation. Curr. Biol. 25, R81–R92. doi: 10.1016/j.cub.2014.11.013
[4] ↑ Salis, P., Lorin, T., Lewis, V., Rey, C., Marcionetti, A., Escande, M. L., et al. 2019. Developmental and comparative transcriptomic identification of iridophore contribution to white barring in clownfish. Pigment Cell Melanoma Res. 32:391–402. doi: 10.1111/pcmr.12766
[5] ↑ Yamaguchi, M., Yoshimoto, E., and Kondo, S. 2007. Pattern regulation in the stripe of zebrafish suggests an underlying dynamic and autonomous mechanism. Proc. Natl. Acad. Sci. U.S.A. 104:4790–93. doi: 10.1073/pnas.0607790104
[6] ↑ Yamanaka, H., and Kondo, S. 2014. In vitro analysis suggests that difference in cell movement during direct interaction can generate various pigment patterns in vivo. Proc. Natl. Acad. Sci. U.S.A. 111:1867–72. doi: 10.1073/pnas.1315416111
[7] ↑ Bullara, D., and De Decker, Y. 2015. Pigment cell movement is not required for generation of Turing patterns in zebrafish skin. Nat. Commun. 6:6971. doi: 10.1038/ncomms7971
[8] ↑ Volkening, A., and Sandstede, B. 2018. Iridophores as a source of robustness in zebrafish stripes and variability in Danio patterns. Nat. Commun. 9:3231. doi: 10.1038/s41467-018-05629-z
[9] ↑ Patterson, L. B., and Parichy, D. M. 2019. Zebrafish pigment pattern formation: insights into the development and evolution of adult form. Annu. Rev. Genet. 53:505–30. doi: 10.1146/annurev-genet-112618-043741
