Abstract
For humans, the ability to jump is an indicator of physical fitness and the ability to move well. To figure out how to jump higher, one solution is to look at animals that do it very well, like grasshoppers. These animals have a tiny mechanism in their knees that works like a sling and enables them to jump very high. Given how well this sling-like mechanism works, could bigger animals—or humans—use it to make huge jumps? The answer, surprisingly, is no: increasing body size makes animals better at producing energy with sling-like mechanisms, but it also increases the energy required to achieve the same jump height. By reading this article, you will learn how physics and geometry help biologists answer a question about how animals move. Let us jump right in!
Why Study Jumping?
Jumping is an essential ability for humans and animals. The better the overall function of the leg muscles, the greater the push during the take-off phase, and the greater the jump height. Hence, jumping ability indicates a person’s physical fitness and their ability to move well. So, by learning how to maximize jump height, scientists can improve the function of human muscles and people’s fitness and health.
To learn how to improve humans’ jumping ability, scientists can look at animals that are exceptional at jumping. Grasshoppers are a good example (Figure 1). For grasshoppers, being proficient jumpers is necessary to escape from predators. They have developed an outstanding ability to quickly jump high and far. Despite being small, grasshoppers can jump 30 cm in height (more than 10 times their body height) and 1 m in length! Do they have a secret for this outstanding jumping ability? If so, could we humans use the same trick to make giant jumps?

- Figure 1 - Grasshoppers have powerful rear legs that help them to jump high and far.
- Those legs contain a muscle called the extensor tibiae, which is attached to elastic structures in the grasshopper’s knee [source: https://pxhere.com/en/photo/771762. Regulated by the Creative Commons License (CC0 Public Domain)].
The Secret of Tiny Grasshoppers Making Giant Jumps
Grasshoppers jump like tiny slings. When you use a sling, you stretch an elastic rubber cord containing the object to throw, and then you release them together, throwing the object far away almost instantly. Grasshoppers do the same, thanks to specialized structures in their knees.
Grasshoppers have six legs. The two longest legs, closest to the rear of the insect, are used to jump. There is a muscle in each back leg called the extensor tibiae. This muscle is small but very strong: it could lift the equivalent of a 1.5 kg bottle of water [1]! There are also elastic structures in grasshoppers’ knees, pulled by the strong extensor tibiae muscle, that work like an elastic cord [2], and a mechanism that allows grasshoppers to lock and unlock the knee almost instantly [3]. The muscle, the elastic cord, and the knee locking/unlocking mechanism are used together to mimic a sling (Figure 2A).
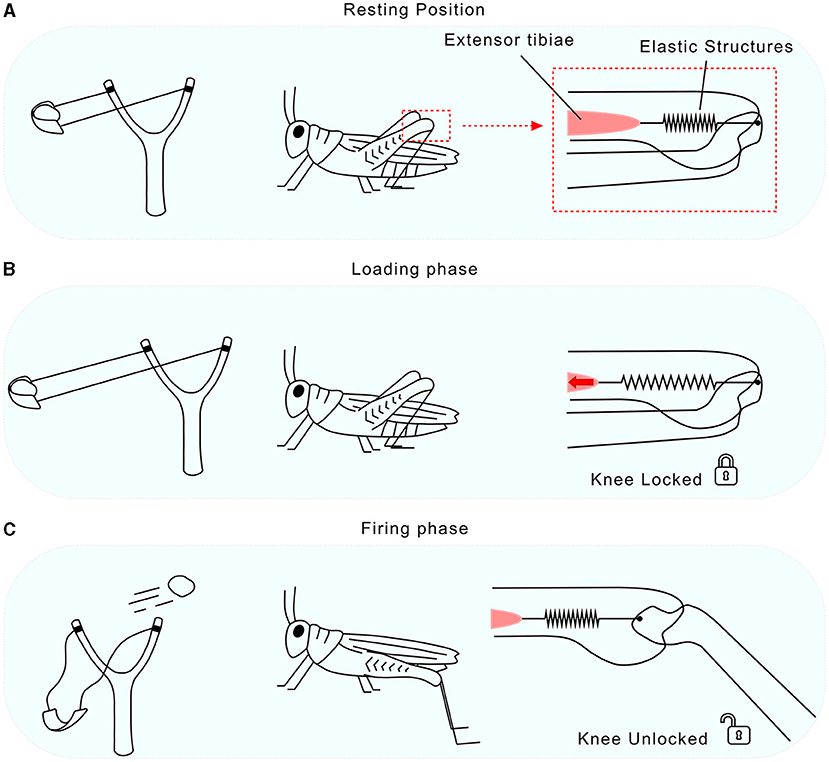
- Figure 2 - (A) Resting position, (B) loading phase, and (C) firing phase in a sling and for a grasshopper.
- The column on the right shows what is happening in a grasshopper’s knee at each phase. In both the sling and grasshopper’s knee, the elastic cord is pulled during the loading phase (by the extensor tibiae in grasshoppers) and elastic energy is stored. The elastic is then released almost instantly during the firing phase, throwing the object far or propelling the grasshopper high into the air.
When using a sling to throw an object, you start by holding the sling with one hand while the other hand pulls the elastic with the object to throw. The elastic becomes longer and ready to shoot; at this point elastic energy is stored in it, and this phase is called the loading phase (Figure 2B). In the following firing phase, the band is released (Figure 2C): the elastic energy is transferred almost instantly to the object, flinging it far. Grasshoppers jump similarly. In the loading phase the knee is locked, the muscle extensor tibiae is activated, and the elastic cord is pulled, meaning energy is stored in the elastic structures of the knee [3]. In the firing phase, the knee is unlocked while the muscle is still active. The energy stored in the elastic structures is released almost instantly, allowing grasshoppers to jump like a sling, quicker than the blink of an eye. This is why it is hard to catch them!
How Much Energy Does a Grasshopper Need to Jump?
One way to look at jumping is that the body is lifted from the ground to a higher point. This requires energy, which is provided by the sling-like mechanism in the grasshopper’s knee. Physics can help us calculate the exact amount of energy needed.
The energy needed to lift a body is calculated by multiplying the body mass (in kg), gravitational acceleration (9.8 m×s−2), and the vertical distance covered (in m):
It is measured in Joules (J). The body mass of grasshoppers is 2 g (0.002 kg), and they can jump 30 cm (0.3 m) in height. Thus, the energy needed is:
This energy must be produced by the sling-like mechanism in the grasshopper’s knee. The energy given by a sling is the multiplication of the force applied to the elastic (in Newtons) and the lengthening of the elastic (in m), divided by 2:
The extensor tibiae provides the force applied to the elastic, while the lengthening of the elastic is the amount of lengthening of the elastic cord in the knee.
So, what would happen if humans could use the grasshoppers’ trick to jump?
Could Humans Jump Like Grasshoppers?
Now we know the secret that tiny grasshoppers use to jump. But what would happen if large animals, like humans, also used it? Could they make huge jumps? The answer, surprisingly, is no. That is because, with increasing body size, both the ability to store energy in the elastic structures and the energy required to lift the body increase at the same rate.
To illustrate this, let us look at what happens when we increase the size of two simple 3-D objects, one cube with an edge length of 1 and one cube with an edge length of 2 (for this example, the unit of measure is not important). The edge of the second cube is twice that of the first cube. The area of each face of a cube is calculated as length × length, while the volume is length × length × length. Applying these formulas to our cubes:
These formulas show that making the length of each side two times longer makes the area four times greater, and the volume eight times greater. This is illustrated in Figure 3A: each face of the second cube contains four faces of the first cube, and the second cube contains eight smaller cubes. In geometry, this is a general scaling principle: if length doubles (×2), area will be four times bigger (2 × 2 = 4), while volume will be eight times bigger (2 × 2 × 2 = 8) [4].
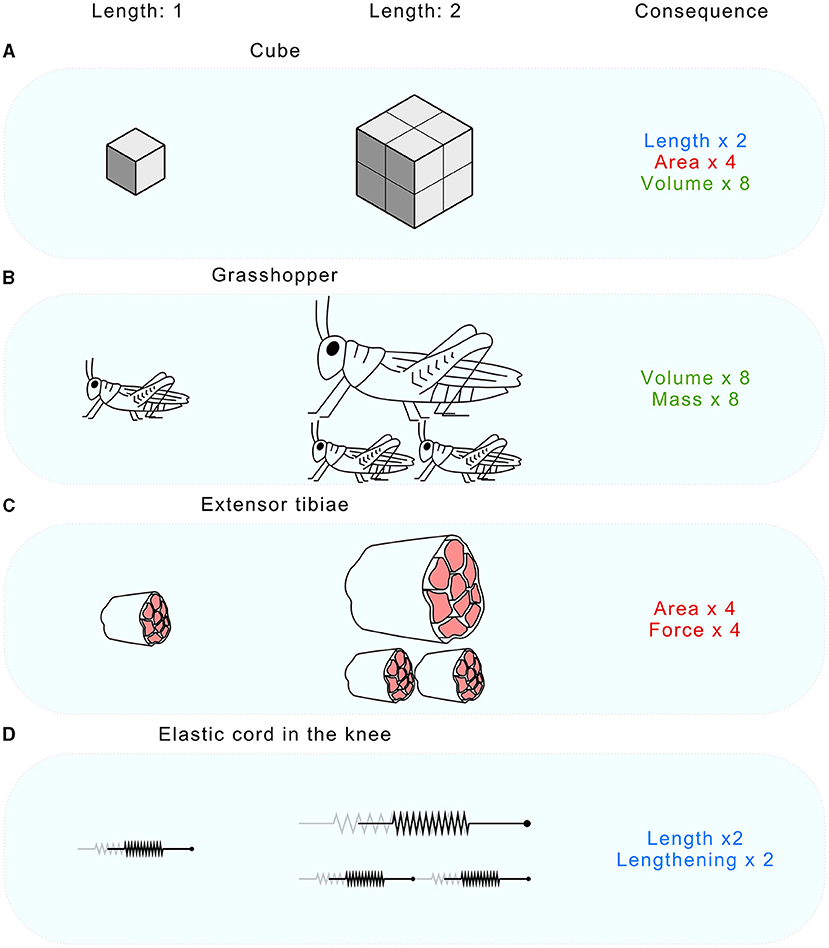
- Figure 3 - (A) In a cube, the area of each face becomes four times wider and the volume eight times bigger when the length of a side is doubled.
- (B) In a grasshopper, the volume becomes eight times bigger, and the mass also eight times greater. (C) In the extensor tibiae, the area of a muscle slice (red) becomes four times wider, and muscle force also becomes four times greater, since force is proportional to this area. (D) The elastic cord in the knee becomes two times longer and the lengthening also becomes two times longer.
Let us apply all of this to grasshoppers. If a grasshopper became twice as long, its volume would become eight times greater (Figure 3B). Mass is the multiplication of density and volume: if density does not change and volume becomes eight times greater, mass also becomes eight times greater. What would happen to the extensor tibiae? The muscle would become twice as long. If we could cut the muscle into slices like a salami, we would notice the area of the slice becoming four times bigger (Figure 3C). The force produced by a muscle is proportional to the area of this slice, so the force of the extensor tibiae would also become four times greater. And what would happen to the elastic cord in the knee? It would become two times longer, and it would lengthen two times more [2] (Figure 3D).
Remember that the energy the sling can produce is the multiplication of the force of the extensor tibiae and the lengthening of the elastic cord, divided by 2:
For a grasshopper with twice the size, force becomes four times greater, and the lengthening of the elastic becomes two times greater: the energy produced by the sling is then eight times greater. Would this make the grasshopper jump eight times higher?
Now remember that the energy needed to lift a grasshopper up (when jumping) is the multiplication of body mass, gravitational acceleration (9.8 m×s−2), and vertical lift:
Unfortunately, by scaling the grasshopper by two times, the body mass increases by eight times, which makes the energy needed for a jump also eight times greater. Thus, both the energy provided by the sling and the energy needed to jump are now eight times greater. It follows that, if scaled by two times, grasshoppers would still jump the same height.
What if a 0.002 kg grasshopper had the same mass as a 70 kg human? We would have to scale up by 33 times: the energy produced by the sling would be 36,000 times greater, but the energy required to jump a certain height would also be 36,000 times greater. The result is that giant grasshoppers and tiny grasshoppers both lift 0.3 m from the ground when jumping. This means the height of giant grasshopper jumps would not be better than what humans are capable of. This is the reason why humans (and big animals in general) do not rely on a sling mechanism like tiny grasshoppers do, and instead power their jumps mostly by shortening their muscles [5].
Next time you meet a grasshopper, do not be scared. Now you know them a little bit better, and you know the secret that makes them jump so high despite their tiny size. You also know that if grasshoppers were as big as humans, they could only jump as high as they do now. Thus, to improve how high they can jump, humans should work on jump training rather than dreaming of jumping like grasshoppers!
Glossary
Extensor Tibiae: ↑ Strong muscle in the rear legs of grasshoppers that powers their jumps.
Elastic Energy: ↑ Energy stored in an elastic structure when it is stretched. This energy is given back when the elastic is suddenly released.
Loading Phase: ↑ Phase that allows elastic energy to be stored. This energy will be used later in the firing phase, to throw an object in a sling or for jumping in grasshoppers.
Firing Phase: ↑ After the loading phase, the elastic is released. By doing this, the elastic energy is transferred to the object, and the object is thrown or a grasshopper jumps.
Gravitational Acceleration: ↑ The force that pulls objects toward the Earth.
Scaling: ↑ Changing the dimensions of an object while keeping the same proportions.
Density: ↑ Ratio between mass and volume of an object. It measures how closely packed together a substance’s particles are.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
We would like to thank Kenan, Mohamad, Kareem, and Mekdad for their involvement in the review process. Kenan is an 18-year-old with a lifelong fascination for the complexity of the living world. His passion soared when he participated in the International Biology Olympiad and proudly earned a bronze medal last year. When he is not unraveling the secrets of life, you will often find him enjoying a refreshing swim or engaging in intense badminton matches with his friends. Mohamad is a passionate eleventh-grader with a profound adoration for STEM disciplines. However, he is particularly fond of biology and physics, and aspire to pursue a degree in either fields. Recently, he was awarded a silver medal in his country’s National Biology Olympiad, earning a spot on the esteemed National Biology Team. He is incredibly honored to have been chosen to represent his country at the 35th International Biology Olympiad, where he aims to expand his understanding of this captivating discipline even further. Kareem is an 18-year-old with a strong passion for biology and research. His ultimate goal is to become a prominent researcher in neuroscience. His journey into this field began back in middle school when he was exploring various disciplines, and neuroscience captured his interest like no other. Besides science, he finds joy in music, competitive debates, and video games. These diverse interests keep him engaged and balanced as he pursues his academic and career aspirations in the fascinating world of neuroscience. Mekdad, at just 16, proudly represents his country in the International Biology Olympiad. His interests revolve around the captivating fusion of mathematics and biophysics. He is intrigued by how these disciplines intersect and complement each other. Moreover, he has a deep passion for delving into scientific literature. Evaluating research critically is not only fulfilling but also allows him to glean valuable insights from these studies. In addition, we thank the Science Mentors for working and guiding our Reviewers through the Review process. We are extremely grateful for the passion of the Science Mentors and the Young Reviewers, which fuels our drive and enthusiasm to share scientific findings with society and with the future generations. Luca Ruggiero was supported by the Alexander von Humboldt Foundation.
References
[1] ↑ Bennet-Clark, H. C. 1975. The energetics of the jump of the locust Schistocerca gregaria. J. Exp. Biol. 63:53–83. doi: 10.1242/jeb.63.1.53
[2] ↑ Rosario, M. V., Sutton, G. P., Patek, S. N., and Sawicki, G. S. 2016. Muscle-spring dynamics in time-limited, elastic movements. Proc. R Soc. Lond. B Biol. Sci. 283:20161561. doi: 10.1098/rspb.2016.1561
[3] ↑ Burrows, M., and Morris, G. 2001. The kinematics and neural control of high-speed kicking movements in the locust. J. Exp. Biol. 204:3471–81. doi: 10.1242/jeb.204.20.3471
[4] ↑ Clemente, C., and Dick, T. J. M. 2023. How scaling approaches can reveal fundamental principles in physiology and biomechanics. J. Exp. Biol. 226:jeb245310. doi: 10.1242/jeb.245310
[5] ↑ Sutton, G. P., Mendoza, E., Azizi, E., Longo, S. J., Olberding, J. P., Ilton, M., et al. 2019. Why do large animals never actuate their jumps with latch-mediated springs? Because they can jump higher without them. Integr. Comp. Biol. 59:1609–18. doi: 10.1093/icb/icz145
