Abstract
Physics is one of the best tools that we have for solving puzzles in our world. These puzzles can range from questions about common phenomena that you see around you—like the wind blowing through a tree’s branches, to questions about very rare and mysterious phenomena that happen only under specific conditions. My journey with physics led me to one very special phenomenon, in which a normal fluid is cooled down and suddenly changes its fundamental properties to become what is called a superfluid. In this article, I will walk you through the fascinating world of superfluids, present some of the interesting things they do, and explain how these materials tie in with the discovery that led me to winning a Nobel Prize in Physics in 2016.
Professor Michael Kosterlitz won the Nobel Prize in Physics in 2016, jointly with professor David Thouless and professor Duncan Haldane, for theoretical discoveries of topological phase transitions and topological phases of matter.
Topology: A Mathematical Language of Shapes
Topology is a mathematical field that discusses the shapes of things and divides objects into classes according to their shapes. One key parameter of any shape is the number of holes that is has in it (for a nice demonstration of topology with pastries, click here). So, for example, a sphere has no holes, whereas a doughnut has one hole (Figure 1A). Therefore, a sphere and a doughnut belong to two separate topological classes. This means that you cannot turn a sphere into a doughnut in a smooth way, because you would have to poke a hole in the sphere and therefore tear the material. In topology, you can distort the material as much as you want but you cannot poke holes or glue pieces together. Thus, you can distort a sphere into a soup bowl so that they are topologically the same. This may seem very strange but the ideas can be useful.
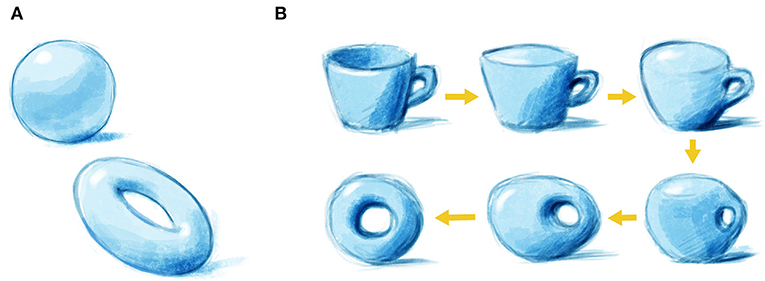
- Figure 1 - Topology and shapes.
- (A) A sphere has no holes, and a doughnut has one hole—therefore, they belong to two separate topological classes. (B) A doughnut and a coffee mug both have one hole and are therefore topologically equivalent. This means we can turn one into the other in a smooth way, without tearing the material or gluing the hole shut, both of which are forbidden in topology. If this happens in the physics, topological ideas are relevant and may be useful.
Now, how about a doughnut and a coffee mug with a handle? They might look different at first, but if you look closely, you will find that they both have one hole. In the eyes of topology, this means that a doughnut and a coffee mug are equivalent. Using the technical term, they have topological equivalence. Therefore, you can transform them into each other in a smooth and continuous way (Figure 1B). So, in this case, the number of holes is called a topological invariant—it stays the same, or is preserved (invariant) with respect to the donut and the coffee mug, even when these objects go through a manipulation that changes their outer appearance.
The language of topology can be useful for describing the properties of certain materials, which are therefore called topological materials. In the next section, we will glimpse how topology helps us identify the differences between materials, and how it also helps us to explain certain unusual and exciting phenomena, like fluids that appear to defy gravity.
Topological Materials: From Plain to Exotic
As we mentioned, topology is a convenient way to describe certain differences that we observe between materials. One family of materials that we all know very well is called insulators. An insulator is a material, such as rubber or plastic, that does not easily conduct electricity. This property is determined by the energy characteristics of the material, meaning the levels of energy that are created by the electrons present in that material. Usually, materials are characterized by the structure of their energy bands—the levels of energy that can be occupied by electrons inside that material. For an insulator, there is an “energy gap” between two energy bands that electrons cannot usually cross, so their movement is limited. For conductors, there is no energy gap, so electrons are free to move between energy levels within the material (to learn more about the energy bands of insulators and conductors, see here). The energy landscape of an insulating system can be classified according to topological invariants—topological properties that are preserved even when the system changes its state. This means that we can spot and classify specific insulators based on the topological properties of their energy states.
One specific group of insulators has attracted a lot of interest over the past 15 years or so. These materials are called topological insulators [1] because they can be classified and described using topological invariants. Topological insulators are special because they are both conducting and insulating at the same time. How can that be? In the middle part of these materials, which is called the bulk, electrons move in small, close loops, and do not travel around (Figure 2C). Therefore, the bulk of topological materials is insulating, much like plastic or rubber (Figure 2A). But, at the surface of these materials, special states form in which electrons can move along the edge (Figure 2C). This means that the surfaces of topological insulators are conducting, much like metals (Figure 2B). You might be thinking to yourself, “Ok, this is cool. But is it useful in any way?” This question occupies many physicists and computer engineers today. Let us have a peek at one possible answer.
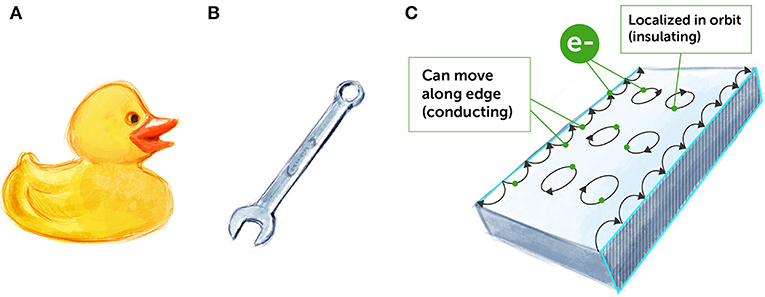
- Figure 2 - Insulators and conductors.
- (A) Rubber is an electrical insulator, so it does not conduct electricity easily. (B) Metals are electrical conductors, so electricity easily flows through them. (C) Topological insulators are unique materials in terms of their conducting properties. In their bulk, their electron move in closed circles (“localized”) and they behave like insulators. On their surfaces, their electron move freely and they act like conductors (“hopping” on the edges).
Are Topological Insulators Useful?
It turns out that the conducting states formed on the surfaces of topological insulators are very stable—they are resilient to defects and perturbations of the material. A major reason that these states are resilient and stable is that their characteristics tend to rely on the entire system—not just on a small part of it or on a few atoms in a specific location. You can think about it like a collective phenomenon of the material as a whole. This means that even if something small—like a local imperfection in the material—is present, it still does not significantly affect the system as a whole, and therefore it does not change the topological state of the system [2].
How can this be useful? The robustness of a topological insulator could be useful for computer applications, as it creates stability. Stability is the most fundamental requirement of a computing element (an element in a computer that performs calculations), since we want these elements to give us consistent results with as few errors as possible. Therefore, topological insulators have an enormous potential for improving computing elements in the future. However, there are major technical challenges involved in this process, so we are quite a long way from using topological insulators in computers—but it might be possible in the future.
I will now take you one step deeper into the enchanted world of topological materials, and present to you my contribution to an explanation of one of the most exotic phenomena in physics, called superfluidity.
A Flying Fluid: The Story of Cold Helium
Did you know that there are fluids that can defy gravity and climb glass walls? These fluids are called superfluids, and they behave very strangely at extremely low temperatures (the temperature at which normal helium becomes superfluid helium is called the Lambda Transition temperature, which is 2.17 K at a pressure of one atmosphere). Due to their exotic nature, superfluids are of great interest to scientists. They allow us to study exceptional physical phenomena that we do not encounter in daily life. The most common example of a superfluid is liquid helium, 4He. You may be familiar with helium as the gas that fills up balloons and makes people’s voices sound funny when they inhale it, but it can exist as a liquid, too at extremely low temperatures close to absolute zero or -273° Celsius.
In 1972, three physicists published a brilliant experiment dealing with thin films of helium [3]. They took a quartz crystal in an atmosphere of Helium gas. By adjusting the pressure of this gas they changed the total amount of Helium adsorbed on the surface of the quartz crystal which would form a layer two or three atoms thick. The quartz crystal has its natural resonant vibration frequency which depends on the total mass of the vibrating crystal. When a thin layer of Helium atoms is stuck to the crystal surface, one naturally expects that these atoms will move with the crystal surface so that their only effect will be to increase the mass of the vibrating body and slightly decrease its resonant frequency. When the physicists looked at the oscillation frequency of the helium covered crystal at low pressure and very low coverage they measured the expected decrease in resonant frequency. However, when the gas pressure and helium coverage was increased, the resonant frequency ceased to follow the expected decrease (Figure 3A) and remained different from the expected value as if the extra Helium was decoupled from the motion of the crystal.
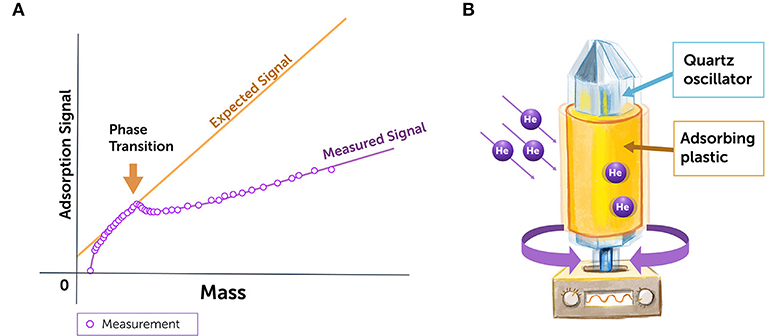
- Figure 3 - Superfluid helium experiment.
- (A) The measured oscillation frequency of the quartz crystal differed from its expected oscillation frequency when a few thin layers of cold helium were adsorbed. The adsorption signal represents the oscillation frequency, and the mass represents the amount of Helium adsorbed on the crystal surface. Helium in its normal state increases the oscillating mass, and decreases its oscillation frequency. But if some of the helium becomes superfluid, it does not increase the oscillator’s mass the same way, so the oscillation frequency is reduced less than it would be with normal helium (Adapted from Chester et al. [3]). (B) In a later experiment [4] which involved much lower frequency oscillations, a plastic Mylar sheet was wrapped round a quartz torsional oscillator rod, 4He gas adsorbed on the Mylar sheet and the resonant frequency and dissipation measured. The principle of this experiment was the same but much more accurate and detailed results were obtained.
A later experiment took a strip of plastic and wrapped it around an oscillating rod made of quartz (Figure 3B). When you vibrate a crystal-like quartz, it has a natural frequency at which it moves, called its oscillation frequency. So, the first thing the physicists did was to measure the natural oscillation frequency of the rod with the roll of plastic around it. Then they increased the pressure of the Helium gas surrounding the oscillating rod and measured the oscillation frequency of the quartz rod again. When helium atoms meet the surface of the adsorbing plastic, they normally adsorb (lock onto) it, creating a thin film around the rod and increasing its mass. As a result, there is a slight reduction in the natural frequency of oscillation, because heavier crystals oscillate at a lower frequency (move more slowly) than light ones.
The easiest way to interpret this result was that some of the helium film was no longer sticking to the oscillator once it became a superfluid. The difference between normal and superfluid helium has to do with the way they flow. Normal helium gets attached to whatever it tries to flows on, due to a property called dissipation. Superfluid helium, on the other hand, flows freely with no dissipation, and therefore seems to “fly,” or hover, above the material it flows on! You can watch some interesting demonstrations with superfluid helium here and here.
This was a pioneering experiment, showing that thin films of helium become superfluid at low temperatures. The problem was, at that time, there was no theory that could explain this change in behavior in thin-film helium, which is called a phase transition, from normal to superfluid. In fact, a common theory at the time even predicted that such a phase transition should not occur under these conditions and that superfluidity was impossible in a two-dimensional film. In fact, this experiment contradicted a widely accepted tenet of the nature of the low temperature phase of any system. There was a rigorous mathematical theorem which stated that the low temperature phase of the system could not have long range order at any temperature which, according to widely accepted wisdom, meant that there could be no superfluidity in our two-dimensional film. Now there was a major conflict between a rigorous theory which seemed to say that superfluidity in a thin film was impossible while experimental observation said the exact opposite. Clearly, either experiment or theory must be wrong or misinterpreted because experiment showed unambiguously that a thin film of 4He is superfluid and has a phase transition. This is where my then supervisor, Prof. David Thouless, and I came into the picture: we developed a new theory that explains the phase transition of thin films of helium from superfluid to normal fluid and resolved the contradiction between experiment and theory.
Vortices: “Behind The Scenes” of Superfluid Helium
As I mentioned, liquid helium has two phases. In its normal phase, it flows with dissipation, meaning that it interacts with the surface it meets, exchanges energy with that surface, and gets stuck to it. In its superfluid phase, liquid helium flows freely with no dissipation, and acts like it is hovering over the surface it meets. To understand the phase transition between normal and superfluid helium, we had to figure out the mechanism responsible for dissipation. As it turns out, the answer lies in peculiar configurations called vortices (Figure 4), which for quantum mechanical reasons, are the only excitations which can dissipate the flow of a superfluid and explains why the very messy surface of Mylar on which the helium is flowing has no effect on the theory or on the experiment. The only effect of the substrate is on the friction between it and the vortices but it has no effect on the superfluid. For simplicity, you can think of a vortex as a fluid circling around, like when you pull the plug out of a bath and the water swirls around as it goes down the drain. To understand this you will have to learn a lot of physics so just remember that these vortices in the superfluid are the only excitations it is necessary to think about and that, in two dimensions, these vortices interact with each other exactly like little electrically charged particles and these particles can appear and disappear as they like but the total charge of the system must remain zero. These vortices form in neutral pairs with one vortex with counterclockwise and the other with clockwise rotation at very low temperatures, but at higher temperatures these pairs unbind into two free vortices that drift to the edges of the fluid and then vanish there thus reducing the uniform superfluid flow by a small amount (Figure 4B). This is the dissipation seen in the flow of the normal fluid. Since the two states of liquid helium’s flow can be defined as two topological states, liquid helium is also considered to be a topological material—much like the topological insulators we discussed previously (To learn more about topological materials and vortices, see here).
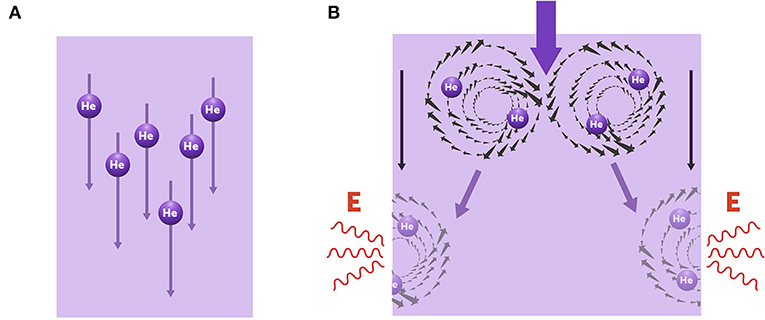
- Figure 4 - Phase transition mechanism in liquid helium.
- (A) In superfluid helium there are no vortices, so the fluid flows freely without dissipation. (B) In normal helium, pairs of vortices are formed (top) and drift to opposite edges of the fluid, where they vanish and release energy (bottom). This process creates dissipation and results in a slower flow with more dissipation.
After discovering that the essential physics of the superfluid system involves the interactions of vortices, we developed a mathematical model to explain the phase transition of liquid helium, and other phase transitions in similar systems, with very high precision [4–7]. This was an important development that took us one big step forward in understanding some of the amazing characteristics of topological materials.
I would like to finish with a few personal notes for young readers about my love for mathematics and physics, and my recommendations for how to live a happy life.
Recommendations For Young Minds
Lovely Symbols: The Beauty of Mathematics and Physics
When I was introduced to algebra in school, I thought to myself “Wow, this is a great way of doing things—much better than arithmetic!,” because algebra allowed me to do lots of mathematical things I could not easily do before. It was like switching on a bright light that suddenly made all sorts of things possible! I immediately loved symbols and the fact that mathematical symbols eliminated a lot of confusion and kept things very simple. I know that this is not the case for everyone because it depends on the way each individual thinks. But for me, working with symbols and equations is fun and exciting, and I enjoy it up to this day. In a way, for me, doing physics is similar to rock climbing (another passion of mine)—you are out in the unknown, on your own, completely responsible for your own actions, trying to navigate your way forward (Figure 5). The advantage with physics is that the penalty for making a mistake is less serious than with rock climbing!

- Figure 5 - Recommendations for Young Minds.
- (A) Working with symbols and equations is similar to rock climbing. You are out exploring the unknown, completely responsible for your own actions, while trying to navigate your way. I find it very exciting.
How to Choose Your Profession
You should do what you love and what you are good at. It is important to be good at whatever you do, and if you are good at it, you are probably going to enjoy it. I also think you should have fun with what you are doing, because if you do not have fun and enjoy your work, it is not worth doing. So, that is a piece of advice I can offer to young readers—have fun in life, because you only have one life, and if you do not have fun, life is not worth living.
Glossary
Topology: ↑ A branch of mathematics that deals with describing shapes of objects.
Topological Materials: ↑ Materials whose properties are described using topology.
Topological Insulators: ↑ Materials that exhibit both insulating properties in their bulk and conducting properties on their surfaces.
Superfluids: ↑ Fluids that flow without dissipation.
Oscillation Frequency: ↑ The frequency at which an object, called an oscillator, vibrates.
Dissipation: ↑ Loss of energy that cannot be reversed without adding external energy.
Phase Transition: ↑ An abrupt switch between two states of a system, in which the properties of the system change. For example, the transition of liquid water into solid ice.
Conflict of Interest
The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
I wish to thank Noa Segev for conducting the interview which served as the basis for this paper, and for co-authoring the paper, Alex Bernstein for providing the figures, and Susan Debad for copyediting the manuscript. Thanks to Dr. Subramanian Ramachandran for his valuable comments on the manuscript.
References
[1] ↑ Moore, J. E. 2010. The birth of topological insulators. Nature. 464:194–8. doi: 10.1038/nature08916
[2] ↑ Qi, X. L. and Zhang, S. C. 2010. The quantum spin hall effect and topological insulators. arXiv preprint. arXiv:1001.1602. doi: 10.1063/1.3293411
[3] ↑ Chester, M., Yang, L. C., and Stephens, J. B. 1972. Quartz microbalance studies of an adsorbed helium film. Phys. Rev. Lett. 29:211. doi: 10.1103/PhysRevLett.29.211
[4] ↑ Bishop, D. J. and Reppy, J. D. 1978. Study of superfluid transition in 2-dimensional 4He films. Phys. Rev. Lett. 40:1727. doi: 10.1103/PhysRevLett.40.1727
[5] ↑ Kosterlitz, J. M. and Thouless, D. J. 1973. Ordering, metastability and phase transitions in two-dimensional systems. J. Phys. C Solid State Phys. 6:1181. doi: 10.1088/0022-3719/6/7/010
[6] ↑ Kosterlitz, J. M. 2016. Kosterlitz–Thouless physics: a review of key issues. Rep. Prog. Phys. 79:026001. doi: 10.1088/0034-4885/79/2/026001
[7] ↑ Hadzibabic, Z., Krüger, P., Cheneau, M., Battelier, B., and Dalibard, J. 2006. Berezinskii–Kosterlitz–Thouless crossover in a trapped atomic gas. Nature. 441:1118–21. doi: 10.1038/nature04851
