תַקצִיר
פיזיקה היא אחד הכלים הטובים ביותר העומדים לרשותנו לפתרון החידות הקיימות בעולם, החל מעיסוק בתופעות נפוצות שאתם רואים סביבכם, כמו משב הרוח בענפי העצים, ועד לשאלות על תופעות נדירות ומסתוריות שמתרחשות רק בתנאים מסוימים. המסע שלי בתחום הפיזיקה הוביל אותי לבחון תופעה מיוחדת מאוד, שבה נוזל רגיל מתקרר ופתאום מְשַנֶה את תכונותיו הבסיסיות והופך לְמה שאנו קוראים לו: נוזל-על. במאמר זה תתלוו אליי למסע בעולם המרתק של נוזלי-העל, אספר לכם על כמה מהדברים המעניינים שקשורים בהם, ואסביר לכם מה הקשר ביניהם לבין התגלית שהובילה אותי לזכייה בפרס נובל לפיזיקה בשנת 2016.
פרופסור מייקל קוֹסְטֶרְלִיץ (Michael Kosterlitz) זכה בפרס נובל לפיזיקה בשנת 2016 עם פרופסור דיוויד ת'אולֶס (David Thouless) ופרופסור דאנקן הוֹלְדֶיין (Duncan Haldane), על תגליות תיאורטיות של מעברֵי מופע (פָזָה) טופולוגיים ומופעים טופולוגיים של חומרים.
טופולוגיה: שפה מתמטית של צורות
טוֹפּוֹלוֹגיה היא תחום במתמטיקה העוסק בצורות של עצמים ומחלק אותם לקבוצות לפי צורותיהם. אחד המאפיינים המרכזיים של כל צורה הוא מספר החורים שיש בה. כך, למשל, לכדור אין חורים, ואילו בדונאט יש חור אחד (איור 1A). לכן, הכדור והדונאט שייכים לשתי קבוצות טופולוגיות נפרדות. זה אומר שאי אפשר להפוך כדור לדונאט בקלות, כי לשם כך ניאלץ לחורר את הכדור ובעקבות כך לקרוע את החומר. בטופולוגיה אפשר לעוות את החומר כמה שרוצים, אבל אין לחורר אותו או להדביק חלקים זה לזה. כך אפשר, למשל, לשנות את צורתו של כדור לכדי צורה של קערת מרק, והם יהיו זהים מבחינה טופולוגית. אף על פי שהרעיונות האלה נראים מוזרים מאוד, הם יכולים להיות שימושיים.
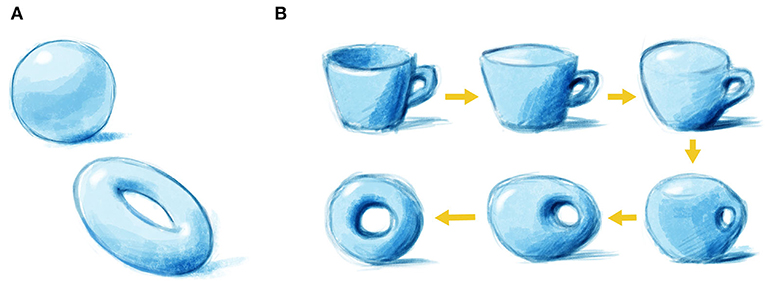
- איור 1 - טופולוגיה וצורות.
- (A) לכדור אין חורים, ולדונאט יש חור אחד – לכן הם שייכים לשתי קבוצות טופולוגיות נפרדות. (B) גם לדונאט וגם לספל הקפה יש חור אחד, ולכן הם שוֵי עֶרֶךְ מבחינה טופולוגית. לכן נוכל להפוך את האחד לשני בצורה חלקה בלי לעשות אף אחת משתי הפעולות האסורות בטופולוגיה: אין לקרוע את החומר ואין לסגור את החור. הרעיונות הטופולוגיים עשויים להיות שימושיים בפיזיקה.
מה דעתכם על הצורות של דונאט ועל ספל קפה שיש לו ידית? הם עשויים להיראות שונים בהתחלה, אבל אם תִבחנו אותם מקרוב, תגלו שלשניהם יש חור אחד. לכן הדונאט וספל הקפה שווי ערך אחד לשני מבחינה טופולוגית. המונח הטכני לתיאור השוויון הזה הוא ''שקילוּת טופולוגית'', כלומר אפשר להפוך אחד לשני בצורה חלקה ומתמשכת (איור 1B). מספר החורים אינו משתנה, ונקרא ''שְׁמוּרָה טופולוגית'' (invariant topology). המשמעות היא שגם כאשר העצמים הללו עוברים מניפולציה שמשנה את המראה החיצוני שלהם, הטופולוגיה שלהם אינה משתנה.
שפת הטופולוגיה יכולה להיות שימושית כשרוצים לתאר את תכונותיהם של חומרים מסוימים, אשר מכונים חומרים טוֹפּוֹלוֹגִיים. בחלק הבא נציץ אל עולם הטופולוגיה, ונראה איך היא עוזרת לנו לזַהוֹת את ההבדלים בין חומרים, ולהסביר תופעות חריגות ומלהיבות, כמו נוזלים שנראים כאילו הם מתנגדים לכוח המשיכה.
חומרים טופולוגיים: מהרגיל לאקזוטי
כפי שציינו, טופולוגיה היא דרך נוחה לתאר הבדלים מסוימים שאנו רואים בין חומרים. אחת ממשפחות החומרים שכולנו מכירים היטב נקראת מְבוֹדֵדִים. מבוֹדֵד הוא חומר, כגון גומי או פלסטיק, שאינו מוליך חשמל בקלות. תכונה זו נקבעת על ידי מאפייני האנרגיה של החומר, כלומר על פי רמות האנרגיה שנוצרות על ידי האלקטרונים הנמצאים באותו החומר. בדרך כלל חומרים שונים מאופיינים על ידי רמות האנרגיה שבהן נמצאים האלקטרונים. בחומרים מְבוֹדֵדִים קיים ''פער אנרגיה'' בין שתי רמות אנרגיה, ובדרך כלל האלקטרונים אינם יכולים להתגבר על הפער הזה ולכן תנועתם מוגבלת. בחומרים מוליכים אין פער אנרגיה, ולכן האלקטרונים חופשיים לנוע בין רמות אנרגיה בתוך החומר (למידע נוסף על רצועות אנרגיה של מְבוֹדֵדִים ומוליכים, ראו כאן). אפשר להגדיר את משטח האנרגיה הפוטנציאלית של מערכת מבוֹדֶדֶת לפי שמוּרוֹת טופולוגיות, כלומר התכונות הטופולוגיות נשמרות גם כאשר המערכת מְשַנָה את מַצָבָהּ. זה אומר שאנו יכולים לזַהוֹת ולסוֵּג מְבוֹדֵדִים מסוימים על סמך התכונות הטופולוגיות של מצבֵי האנרגיה שלהם.
קיימת קבוצה מסוימת של חומרים מְבוֹדֵדִים שמשכה עניין רב בחמש-עשרה השנים האחרונות. חומרים אלו נקראים מְבוֹדֵדִים טוֹפּוֹלוֹגִיים [1], כיוון שאפשר לסווג אותם ולתאר אותם באמצעות שמוּרוֹת טופולוגיות. מבוֹדֵדִים טופולוגיים הם מיוחדים, משום שהם גם מוליכים וגם מְבוֹדֵדִים בו זמנית. איך זה ייתכן? בחלק האמצעי של החומרים הללו, הנקרא פְּנים החומר, האלקטרונים אינם נעים בחופשיות, אלא במעגלים קטנים וצפופים (איור 2C). לכן, פְּנים החומר של החומרים הטופולוגיים הוא מבוֹדֵד, בדומה לפלסטיק או לגומי (איור 2A). בניגוד לכך, על פנֵי השטח של חומרים אלה נוצָרים מצבים מיוחדים שבהם אלקטרונים יכולים לנוע לאורך הקצה של החומר (איור 2C). כלומר פנֵי השטח של המְבוֹדֵדִים הטופולוגיים מוליכים כמו מתכות (איור 2B). אולי אתם חושבים לעצמכם, ''יופי, זה מגניב, אבל האם זה בכלל שימושי?'' זאת שאלה שמעסיקה כיום פיזיקאים ומהנדסי מַחשבים רבים. הבה נציץ באחת התשובות האפשריות.
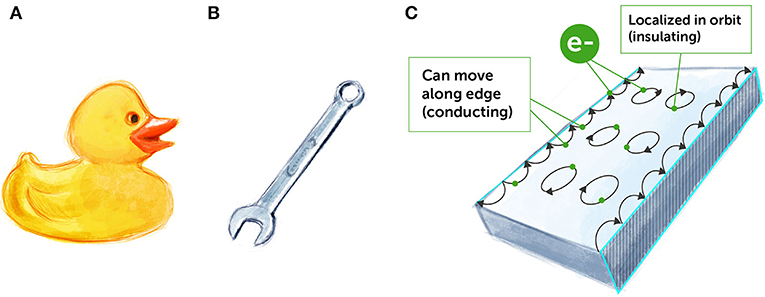
- איור 2 - מְבוֹדֵדִים ומוליכים.
- (A) גומי הוא מְבוֹדֵד חשמלי, ולכן אינו מוליך חשמל בקלוּת. (B) מתכות מוליכות חשמל, כלומר החשמל זורם דרכן בקלוּת. (C) מְבוֹדֵדִים טופולוגיים הם חומרים ייחודיים מבחינת תכונות ההולכה שלהם: במרכז, הנקרא פְּנים החומר, האלקטרונים נעים במעגלים סגורים (''מוגבלים למקומם'') והם מתנהגים כמו מְבוֹדֵדִים. אך על פנֵי השטח של מְבוֹדֵדִים טופולוגיים, האלקטרונים נעים בחופשיות והם פועלים כמו מוליכים (''מקפצים'' על הקצוות).
- Conducting = מוליך;
- Insolating = מבודד;
- Localized in orbit (insulating) = מְמֻקָם במעגל (מְבוֹדֵד)
- Can move along edge (conducting) = יכול לנוע לאורך הקצה (מוליך).
האם מבודדים טופולוגיים הם שימושיים?
מתברר שהמצבים המוליכים הנוצָרים על פנֵי השטח של מְבוֹדֵדִים טופולוגיים יציבים מאוד – הם עמידים בפני פגמים והפרעות המתרחשות בחומר. אחת הסיבה המרכזיות לכך שמצבים אלה הם עמידים ויציבים היא שהמאפיינים שלהם נסמכים על המערכת כולה – לא רק בחֶלֶק קטן ממנה או בכמה אטומים במיקום מסוים. זאת תופעה המשותפת לחומר בכללותו, וגם אם קיים פְּגם מקומי בחומר, אין לו השפעה מהותית על המערכת כולה, ולכן הוא אינו מְשַנֶה את המצב הטופולוגי שלה [2].
כיצד נוכל להשתמש בתכונה הזאת? אפשר לרתום את חוסנם של המְבוֹדֵדִים הטופולוגיים עבור יישומים בתחום המחשבים, כיוון שהם מְסַפְּקִים יציבוּת. יציבוּת היא הדרישה הבסיסית ביותר של רכיבי המִחְשוּב (רכיבים במחשב שמבַצעים חישובים). הסיבה היא שחשוּב לנו שהרכיבים הללו יספקו תוצאות שיהיו עקביות ככל האפשר, ועם כמה שפַּחות שגיאות. בזכות תכונות אלו, למְבוֹדֵדִים הטופולוגיים יש פוטנציאל עצום לשיפור רכיבֵי המִחְשוּב בעתיד. עם זאת, ישנם אתגרים טכניים גדולים המעורבים בתהליך שכזה, כך שאנחנו רחוקים למדַי משימוש במְבוֹדֵדִים טופולוגיים במַחשבים, אך אולי זה יהיה אפשרי בעתיד.
כעת נצלול לתוך עולמם הקסום של החומרים הטופולוגיים. בחלק הבא אציג בפניכם את תרומתי להסבר של אחת התופעות האקזוטיות ביותר בפיזיקה הנקראת נְזִילוּת-על.
נוזל מעופף: סיפורו של ההליום הקַר
האם ידעתם שיש נוזלים שיכולים לקרוא תיגר על כוח המשיכה ולטפס על קירות זכוכית? נוזלים אלו נקראים נוזלֵי-על, ובטמפרטורות נמוכות מאוד הם מתנהגים בצורה מוזרה ביותר (הטמפרטורה שבה הליום רגיל הופך לנוזל-על נקראת טמפרטורת המעֲבר לָמְבְּדָה, שהיא K2.17° בלחץשלאַטְמוֹסְפֶרָהאחת). בשל אופיים האקזוטי, המדענים מגלים עניין רב בנוזלֵי-העל, המאפשרים לנו לחקור תופעות פיזיקליות יוצאות דופן שאיננו נתקלים בהן בחיי היום-יום. הדוגמה הנפוצה ביותר לנוזל-על היא הליום נוזלי – 4He. אתם ודאי מכירים את ההליום בתור גז למילוי בלונים שגורם לקול להישמע מצחיק כששואפים אותו, אבל הוא יכול להתקיים גם כנוזל, בטמפרטורות נמוכות במיוחד, הקרובות לאפס המוחלט (0°K שהן מינוס 273 מעלות צלזיוס).
בשנת 1972 שלושה פיזיקאים פרסמו ניסוי מבריק שבו נערכו תצפיות בשכבות דקות של הליום (Helium) [3]. הם לקחו גביש קְוַרְץ ושָׂמוּ אותו באטמוספרה של גז הליום. הם התאימו את הלחץ של הגז, כך שהכמות הכוללת של הליום שנקשר לפני השטח של גביש הקוורץ השתנתה, ונוצרה על גביו שִכבה בעובי של שניים או שלושה אטומים. התדר של רֶטֶט התהודה הטבעי של גביש הקוורץ תלוי במסה הכוללת של הגביש הרוטט. כאשר שכבה דקה של אטומי הליום נדבקת לפנֵי הגביש, הציפייה הטבעית היא שהאטומים הללו ינועו עם פנֵי הגביש כך שהשפעתם היחידה תהיה הגדלת מסת הגוף הרוטט ולהקטין מעט את תדירוּת התהודה שלו. כשהפיזיקאים מדדו את תדירוּת התנודה של הגביש המכוסה הליום בלחץ נמוך ובכיסוי מצומצם מאוד, הם ראו את הירידה שציפו לראות בתדר התהודה. עם זאת, כאשר לחץ הגז וכיסוי ההליום גברו, תדר התהודה כבר לא ירד כפי שחשבו (איור 3A) – הערך שלו היה שונה מהצפוי, כאילו ההליום שהתווסף התנתק מתנועת הגביש.
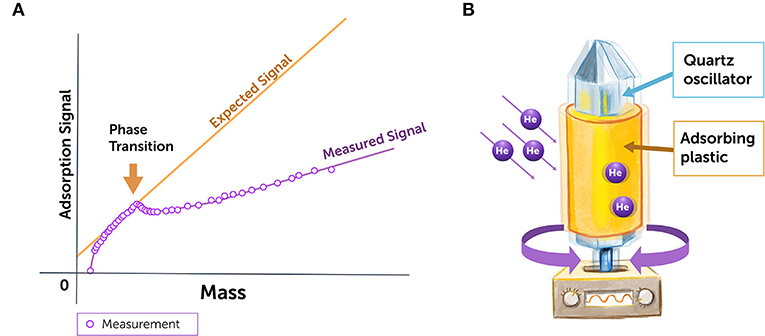
- איור 3 - ניסוי ההליום במצב נוזל-על.
- (A) כאשר נספחו לפנֵי השטח של הגביש כמה שכבות דקות של הליום קר, תדירות התנודה של גביש הקוורץ שנמדדה הייתה שונה מתדירות התנודה שציפינו לה. אות הספיחה (adsorption signal) מייצג את תדירות התנודה, והמסה מייצגת את כמות ההליום שנספח על פני הגביש. ההליום במצבו הרגיל מגדיל את המסה המתנודדת, ומקטין את תדירות התנודה שלה. אם חלק מההליום הופך לנוזל-על, הוא אינו מגדיל את המסה של המַתְנֵד באותו האופן, ולכן תדירות התנודה היא פחותה מזאת של ההליום הרגיל (האיור נלקח מ-[3]). (B) בניסוי שנערך לאחר מכן [4], שֶכָּלל תנודות בתדירות נמוכה בהרבה, כרכו יריעת מיילר (Mylar) עשויה מפלסטיק סביב מוט מַתְנֵד קוורץ שמסתובב הלוך ושוֹב. במקרה הזה גז ה-4He נספח על יריעת הפלסטיק, והמדענים מדדו את תדר התהודה ואת הדִיסִיפָּצְיָה. העיקרון של ניסוי זה היה זהה, אך התוצאות שהתקבלו היו הרבה יותר מדויקות ומפורטות.
- Adsorption signal = אות הספיחה;
- Mass = מסה;
- Phase Transition = מעֲבר בין מצבים;
- Expected Signal = האות המצוּפה;
- Measured Signal = האות שנמדד;
- Quartz oscillator = מַתְנֵד קוורץ;
- Adsorbing plastic = פלסטיק סופח;
- Measurement = מדידה.
בניסוי שהתקיים לאחר מכן [4] המדענים כרכו יריעת פלסטיק סביב מוט מַתְנֵד העשוי קוורץ (איור 3B). כאשר יוצרים רֶטֶט בקוורץ שהוא דמוי-גביש, הוא נע בתדירות מסוימת, הנקראת תדירוּת התנודה. בהתחלה הפיזיקאים מדדו את תדירות התנודה הטבעית של המוט שגליל הפלסטיק כרוך סביבו. לאחר מכן, הם הגבירו את הלחץ של גז ההליום המקיף את המוט המתנודד, ומדדו שוב את תדירות התנודה של מוט הקוורץ. כאשר אטומי ההליום פוגשים את פני הפלסטיק הסופח, הם בדרך כלל נספחים בו (כלומר נקשרים אליו) ויוצרים מעטה דק מסביב למוט ומגדילים את המסה שלו. כתוצאה מכך, תדר התנודה הטבעי פוחת מעט, כיוון שגבישים כבדים יותר מתנודדים בתדר נמוך יותר (זזים לאט יותר) מאשר גבישים קלים.
המשמעות של תוצאה זו היא שחלק ממעטה ההליום כבר לא היה קשור למַתְנֵד ברגע שהוא הפך לנוזל-על. ההבדל בין הליום רגיל להליום במצב נוזל-על טמון באופן שבו הם זורמים. הליום רגיל נקשר לכל דבר שהוא זורם עליו בשל תכונה הנקראת דִיסִיפָּצְיָה. לעומת זאת, הליום במצב נוזל-על זורם בחופשיות, ולכן נראה שהוא ''עף'' או מרחף מעל החומר שעליו הוא זורם! אתם יכולים לצפות בכמה הדגמות מעניינות שבהן משתמשים בהליום במצב נוזל-על כאן וכאן.
היה זה ניסוי פורץ דרך שהראה ששכבות דקות של הליום הופכות לנוזלֵי-על בטמפרטורות נמוכות. הבעיה הייתה שבאותה התקופה לא הייתה תיאוריה שהסבירה את השינוי הזה, שנקרא מעֲבר מופע (פָזָה) במעֲבר מהליום רגיל להליום במצב נוזל-על. אחת התיאוריות הנפוצות באותה התקופה אפילו גָרסה כי מעֲבר מופע שכזה אינו אמור להתרחש בתנאים אלו, וכי נזילוּת-על היא בלתי אפשרית בשכבה דו-ממדית. למעשה, הניסוי הזה סתר את הדרך שבה תפסו בזמנו את אופיין של כל המערכות במצב של טמפרטורה נמוכה. הייתה אז טענה מתמטית שקבעה שבשלב של טמפרטורה נמוכה של מערכת כלשהי, סדר ארוך-טווח אינו יכול להתקיים בשום טמפרטורה. כלומר לפי הדעה המקובלת, פירושו שנזילות-על אינה יכולה להתקיים בשכבה דו-ממדית כמו זו שקיימת בניסוי שראינו. לאור תוצאות הניסוי, נוצרה סתירה מהותית בין התיאוריה המתמטית, לפִיה נראה שנזילות-על אינה אפשרית בשכבה דקה, ובין תוצאות התצפיות הניסיוניות, שהצביעו על ההיפך הגמור. היה ברור שהייתה טעות או פירוש לא נכון בניסוי או בתיאוריה, כיוון שהניסוי הראה באופן שאינו משתמע לשתי פנים ששכבה דקה של 4He היא נוזל-על, ושמתקיים בה מעֲבר בין מופעים. או אז, המנחה שלי דאז פרופ' דיוויד ת'אולֶס (David Thouless) ואנוכי פיתחנו תיאוריה חדשה שמסבירה את המעֲבר בין המופעים של שכבות הליום דקות מנוזל-על לנוזל רגיל, וכך פתרנו את הסתירה בין הניסוי לבין התיאוריה שהייתה ידועה עד כה.
מערבולות: ''מאחורי הקלעים'' של ההליום במופע של נוזל-על
כפי שציינתי, להליום נוזלי יש שני מופעים. במופע הרגיל שלו, כשההליום זורם מתרחשת דיסיפציה, כלומר נוצר מגע בינו לבין המשטח שעליו הוא זורם, ואז נוצרים חילופי אנרגיה עם אותו המשטח, וההליום נדבק אליו. כשההליום הוא במופע של נוזל-העל שלו, ההליום הנוזלי זורם בחופשיות ללא דיסיפציה, ומתנהג כאילו הוא מרחף מעל פני השטח שהוא בא איתו במגע. כדי להבין את מעֲבר המופעים בין הליום רגיל לבין נוזל-העל שלו, פרופ' ת'אולֶס ואני נדרשנו להבין את המנגנון האחראי לדיסיפציה. מתברר שהתשובה טמונה בתצורות יוצאות-דופן הנקראות מערבולות (איור 4). מִסיבות של מכניקה קוונטית, המערבולות במצב של עִירוּר (העלאת ההליום הנוזלי לרמת אנרגיה גבוהה יותר) הן הגורם היחיד שמסוגל ליצור דיסיפציה בזרימת נוזל-העל.
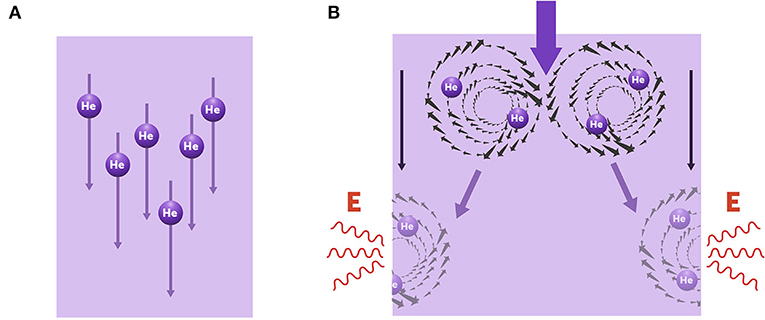
- איור 4 - מנגנון מעֲבר המופע בהליום נוזלי.
- (A) כיוון שבהליום שבמצב של נוזל-על אין מערבולות, הנוזל זורם בחופשיות ללא דיסיפציה. (B) בהליום רגיל נוצרים זוגות של מערבולות הנסחפות לשוליים מנוגדים של הנוזל (בחלק העליון של האיור). שם הן נעלמות ומשחררות אנרגיה (בחלק התחתון של האיור). בתהליך זה מתרחשת דיסיפציה והתוצאה היא זרימה איטית יותר ודיסיפציה מוגברת.
- He = הליום (Helium);
- E = אנרגיה (Energy).
תופעה זו מסבירה גם מדוע ליריעת הפלסטיק ה''מבולגנת'' שעָלֶיהָ זורם ההליום, אין השפעה על התיאוריה או על הניסוי. ההשפעה היחידה של היריעה היא על החיכוך בינה לבין המערבולות, אך אין לה השפעה על נוזל-העל. כדי להבין את הדברים בצורה פשוטה יותר, אתם יכולים לדמיין את המערבולות כנוזלים המסתחררים סביב, כפי שקורה כששולפים את הפקק באמבטיה מלאת מים, והם מתנקזים ממנה בסחרור. כדי להבין זאת תצטרכו ללמוד פיזיקה לעומק, אז כרגע אתם יכולים פשוט לזכור שהמערבולות הללו בנוזל-העל הן הגורמים המעוררים היחידים שאנחנו צריכים להכיר. עלֵינו לדעת שבדוּ-מֵמַד המערבולות הללו מקיימות אינטראקציה זו עם זו בדיוק כמו חלקיקים קטנים טעונים חשמלית שיכולים להופיע ולהיעלם באקראי, אבל לבסוף המטען החשמלי הכולל של המערכת נשאר אפס. בטמפרטורות נמוכות מאוד המערבולות הללו יוצרות זוגות ניטרליים, כלומר הן מנטרלות אחת את השנייה: אחת המערבולות מסתובבת נגד כיוון השעון, והשנייה מסתובבת עם כיוון השעון. בטמפרטורות גבוהות יותר הזוגות מתפרקים, ומתקבלות שתי מערבולות נפרדות שנסחפות לשולי הנוזל ונעלמות שם, וכך הן מפחיתות במעט את הזרימה האחידה של נוזל-העל (איור 4B). למעשה, זוהי דיסיפציה הנצפית בזרימת הנוזל הרגיל. כיוון שאפשר להגדיר את שני המצבים של זרימת ההליום הנוזלי כשני מצבים טופולוגיים, ההליום הנוזלי נחשב גם הוא לחומר טופולוגי – בדומה למְבוֹדֵדִים הטופולוגיים שדנו בהם קודם לכן (למידע נוסף על חומרים טופולוגיים ומערבולות, ראו כאן).
לאחר שגילינו שהפיזיקה החיונית של מערכת נוזל-העל כרוכה בהשפעה ההדדית של מערבולות, פיתחנו מודל מתמטי המיועד להסביר בדיוק גבוה מאוד את מעֲבר המופעים של ההליום הנוזלי, וכן מעֲברי מופעים במערכות דומות [4–7]. הייתה זאת התפתחות חשובה שקידמה אותנו מאוד בהבנת כמה מהמאפיינים המדהימים של החומרים הטופולוגיים.
ברצוני לסיים בכמה הערות אישיות לקוראים הצעירים על אהבָתי למתמטיקה ולפיזיקה ובהמלצות שלי לחיים מאושרים.
המלצות למוחות צעירים סמלים נפלאים: היופי שבמתמטיקה ובפיזיקה
כשהתוודעתי לאלגברה בבית הספר חשבתי לעצמי, ''איזה יופי! זו דרך הרבה יותר טובה מְחֶשבון לפתור בעיות!'', מפני שהאלגברה אפשרה לי לעשות הרבה פעולות מתמטיות שקודם לכן לא יכולתי לעשות בקלות. הרגשתי כאילו מישהו הדליק את האור ואִפשר לי פתאום לראות טוב יותר, והצלחתי לעשות דברים שלא יכולתי קודם! מייד התאהבתי בסמלים, ובעובדה שהסמלים המתמטיים חסכו הרבה בלבול ופישטו מאוד את הדברים. אני יודע שלא כולם חשים כך, כי זה תלוי בדרך שבה המוח של כל אחת ואחד מאיתנו עובד, אבל עבורי העבודה עם סמלים ומשוואות היא מהנה ומרגשת עד היום. במובן מסוים, העיסוק בפיזיקה דומה לטיפוס הרים (שהיא עוד אחת מתשוקותיי) – במצב כזה אתם נמצאים לבדכם במָקום לא-נודע, יש לכם אחריות מלאה על הפעולות שלכם, ואתם מנסים לנווט את דרככם כדי להתקדם (איור 5). היתרון בפיזיקה הוא שה''עונש'' על טעות הוא פחות חמוּר מאשר בטיפוס הרים!

- איור 5 - המלצות למוחות צעירים.
- העבודה עם סמלים ועם משוואות דומה לטיפוס הרים: אנחנו אחראים לגמרי לפעולותינו וחוקרים את הלא-נודע, בעוד שאנו מנסים למצוא את דרכינו. בעיניי זה מלהיב מאוד.
איך לבחור מקצוע
כדאי לכם לעשות את הדברים שאתם אוהבים ושאתם טובים בהם. חשוּב להיות טובים בְּמה שאתם עושים, כי אם אתם טובים במשהו, כנראה שתיהנו מהעשייה שלכם! לדעתי חשוב גם ליהנות ממה שעושים, כי אם לא תיהנו מהעבודה שלכם – לא שווה לעשות אותה. אז זאת העצה שאני מציע לקוראים הצעירים: תיהנו מהחיים שלכם, כי חיים רק פעם אחת, ואם לא נהנים – אז מה שווים החיים?
מילון מונחים
טוֹפּוֹלוֹגיה (Topology): ↑ ענף במתמטיקה העוסק בתיאור צורות של עצמים.
חומרים טוֹפּוֹלוֹגִיים (Topological Materials): ↑ חומרים שתכונותיהם מתוארים באמצעות טופולוגיה.
מְבוֹדֵדִים טוֹפּוֹלוֹגִיים (Topological Insulators): ↑ חומרים בעלי תכונות של מְבוֹדֵדִים במרכזם ותכונות של מוליכים על פני השטח שלהם.
נוזלֵי-על (Superfluids): ↑ נוזלים שזורמים ללא דיסיפציה.
תדירוּת התנודה (Oscillation Frequency): ↑ התדירות שבה מַתְנֵד רוטט.
דִיסִיפָּצְיָה (Dissipation): ↑ אובדן אנרגיה שאי אפשר להחזיר ללא הוספה של אנרגיה חיצונית.
מעֲבר מופע (פָזָה) (מעֲבר בין מצבי צבירה) (Phase Transition): ↑ מעֲבר פתאומי בין שני מצבים של מערכת שבהם מאפייני המערכת משתנים. למשל, מעֲבר של מים ממצב צבירה נוזלי למצב צבירה מוצק – קֶרַח.
הצהרת ניגוד אינטרסים
המחברים מצהירים כל המחקר נערך בהעדר כי קשר מסחרי או פיננסי שיכול להתפרש כניגוד אינטרסים פוטנציאלי.
תודות
ברצוני להודות לנועה שגב על עריכת הריאיון שהיווה את הבסיס למאמר זה, ועל כתיבה משותפת של המאמר. תודה לאלכס ברנשטיין עבור האיורים, ולסוזן דיבַּד (Susan Debad) על העריכה של כתב היד. תודה לד''ר סַבְּרַמַנִיאָן רַמַצַ'נְדְרַן (Subramanian Ramachandran) על הערותיו החשובות על כתב היד.
מקורות
[1] ↑Moore, J. E. 2010. The birth of topological insulators. Nature. 464:194–8. doi: 10.1038/nature08916
[2] ↑ Qi, X. L. and Zhang, S. C. 2010. The quantum spin hall effect and topological insulators. arXiv preprint. arXiv:1001.1602. doi: 10.1063/1.3293411
[3] ↑ Chester, M., Yang, L. C., and Stephens, J. B. 1972. Quartz microbalance studies of an adsorbed helium film. Phys. Rev. Lett. 29:211. doi: 10.1103/PhysRevLett.29.211
[4] ↑ Bishop, D. J., and Reppy, J. D. 1978. Study of superfluid transition in 2-dimensional 4He films. Phys. Rev. Lett. 40:1727. doi: 10.1103/PhysRevLett.40.1727
[5] ↑ Kosterlitz, J. M., and Thouless, D. J. 1973. Ordering, metastability and phase transitions in two-dimensional systems. J. Phys. C Solid State Phys. 6:1181. doi: 10.1088/0022-3719/6/7/010
[6] ↑ Kosterlitz, J. M. 2016. Kosterlitz–Thouless physics: a review of key issues. Rep. Prog. Phys. 79:026001. doi: 10.1088/0034-4885/79/2/026001
[7] ↑ Hadzibabic, Z., Krüger, P., Cheneau, M., Battelier, B., and Dalibard, J. 2006. Berezinskii–Kosterlitz–Thouless crossover in a trapped atomic gas. Nature. 441:1118–21. doi: 10.1038/nature04851
