תַקצִיר
מדענים משתמשים בתחום מתמטי שנקרא טוֹפּוֹלוֹגיה כדי לחקור את צורותיהם של אובייקטים. חלק חשוב בטופולוגיה הוא ספירה של מספר הפיסות ומספר החורים באובייקט, וחוקרים משתמשים במידע הזה כדי לקבץ אובייקטים לסוגים שונים. לדוגמה, אובייקט בצורת טבעת מכיל את אותו מספר החורים ואת אותו מספר הפיסות כמו כוס תה עם ידית אחת, אך הוא שונה מכדור. במחקרים שמזכירים פעילויות כמו ''חיבור הנקודות'', מדענים משתמשים ברעיונות מתחום הטופולוגיה כדי לחקור את ה''צורה'' של נתונים. רעיונות ושיטות מטופולוגיה משמשים לחקירת המבנים המסתעפים של עורקים בעלים, של הצבעות בבחירות, של תבניות טיסה, במודלים של להקות ציפורים ועוד.
מהי צורה?
צורות הן כל כך יסודיות לקיומנו, שמוחותינו מתחילים לשים לב אליהן כבר בגיל ארבעה או חמישה חודשים. אנו רגילים לתאר צורות שכיחות כמו קווים, עיגולים וקוביות, אולם מה לגבי אובייקטים מורכבים יותר, כמו דרקון או פּוֹקִימוֹן או בן אדם?
טופולוגיה היא ענף במתמטיקה שעוסק בצורות של דברים [2 ,1]. כדי לסייע לנו להבין טופולוגיה, נבחן גומייה עגולה. אנו מעוניינים לתאר את התכונות של אובייקט שנשאר אותו הדבר אם אנו מותחים אותו, מכווצים או מעקמים, אך בלי שנדביק דברים יחד, או נשבור את האובייקט, או ניצור נקודות חדות כלשהן. מנקודת מבט טופולוגית, מאחר שאנו יכולים למתוח את הגומייה לצורה אליפטית, ניתן לומר שהעיגול והאליפסה הם זהים טופולוגית. אך הגומייה אינה זהה טופולוגית ל מֵיתָר, מאחר שלגומייה יש חור במרכז ואִלּוּ למיתר אין. זכרו שאסור לנו להדביק את קצוות המיתר יחד, ואיננו יכולים לחתוך את הגומייה.
על ידי פענוח אֵילוּ צורות שְׁקִילוֹת זו לזו באופן המיוחד הזה, אנו יכולים להפריד את הצורות לקבוצות שונות. בתור דוגמה, נשייך את האותיות במילה ''פוקימון'' באנגלית (Pokémon) לאובייקטים זהים טופולוגית – ראו אנימציה קצרה בקטע וידיאו 1. האותיות ''P'' ו-''o'' שייכות לאותה הקבוצה, מאחר שאנו יכולים לדחוס את החלק התחתון של ''P'' כלפי מעלה ואז למתוח את החור לצורה של האות ''o''. כתוצאה מכך, ''P'' ושני המופעים של האות ''o'' יוצרים קבוצה אחת של אותיות זהות טופולוגית. האותיות ''m'' ,''k'' ו-''n'' יוצרות קבוצה אחרת, מאחר שאנו יכולים להפוך כל אחת מהן לנקודה על ידי דחיסה ועיקום שלהן. האות הנותרת, ''é'', היא אות מעניינת. ללא ההטעמה שלה, היינו יכולים לכווץ את הקצה העגול של ה-''e'' אל הצד השמאלי של חצי המעגל בחלק העליון של האות. לאחר מכן, יכולנו למתוח את חצי המעגל לצורה של האות ''o'', אשר ממקמת אותה באותה הקבוצה כמו ''P'' ו-''o''. אולם, עם ההטעמה, ל-é יש שתי פיסות נפרדות שלא ניתן להדביקן יחד, ולכן היא שייכת לקבוצה משל עצמה.
צורות שהן באותה הקבוצה חולקות מאפיינים חשובים. אף על פי שהפרטים של הצורות ''P'' ו-''o'' שונים, לכל אחת מהן יש חור אחד שאיננו יכולים להסיר. בניגוד לכך, לאותיות ''m'' ,''k'' ו-''n'' אין חורים כלל. אם נסתכל על האות הגדולה ''B'', ניתן לראות שהיא לא שייכת לאף אחת מהקבוצות האלה, אך היא זהה טופולוגית למספר ''8'', מאחר שגם ל-''B'' וגם ל-''8'' יש שני חורים. מספר הפיסות באובייקט הוא גם חשוב, ולכן ה-''é'' (עם חור אחד ושתי פיסות) שייכת לקבוצה שונה מכל האותיות האחרות שדנו בהן. נסו להפריד את האותיות בשמכם לקבוצות של אותיות זהות טופולוגית.
כעת, נבחן דברים מעניינים אף יותר, על ידי התבוננות בחלק מהפוקימונים עצמם. עבור כל פוקימון באיור 1, סִפְרוּ את כמות הפיסות והחורים. האם אתם יכולים לקבץ אותם יחד בהתבסס על המידע הזה?

- איור 1 - סיווג פוקימונים לצורות שונות.
- כפי שניתן לראות, לפוקימון יש צורות שונות: (A) גַּסְטְלִי, (B) הַנְטֵר ו-(C) גֶּנְגָר. האם אתם יכולים לקטלג את דמויות הפוקימון לצורות שונות בהתבסס על מספר החורים ומספר הפיסות שלהם?
חקירת הטופולוגיה של אובייקטים מוצקים, כמו אלה שדנו בהם עד כה, עשויה להיות מאתגרת, אך כעת חִשְׁבוּ על איורים בפעילויות כמו ''חברוּ-את-הנקודות''. לפנינו אוסף של נקודות, לעיתים קרובות אנו רואים מספיק מהן כדי שיהיה לנו רעיון לגבי איזו צורה נקבל כשנחבר אותן (ראו איור 2). אנשים טובים בזיהוי צורות מראיית נקודות בלבד, אך האם ישנהּ דרך לעשות זאת באופן אוטומטי? אף על פי שסוג הפעילות הזה הוא קשה יותר למחשב מאשר לבן אדם, מתמטיקאים ומדענים אחרים מחפשים דרכים יעילות לעשות זאת באופן אוטומטי, מאחר שאנו מבקשים לבחון אוספי נקודות רבים.

- איור 2 - חיבור נקודות של דמויות פוקימון.
- האם אתם יכולים לדמיין כיצד הפוקימון באיור הזה ייראה כשתחברו את הנקודות? הפוקימונים שאנו מציגים הם: (A) גִּ'יגְלִיפַּף, (B) אִיוִִי ו-(C) בָּטֶרְפְרִי.
טופולוגיה יכולה לסייע לנו למצוא את ההיגיון בכמויות גדולות של נתונים, ואנו יכולים לחשוב על חקירת הטופולוגיה של אוסף נתונים (שנקרא סֶט נתונים) בתור משחק ענקי של ''חברוּ-את-הנקודות''. בחיים האמיתיים, ישנם הרבה סוגי נתונים שונים, אשר לא מגיעים בצורת נקודות על גבי דף. אנו נתמקד בנתונים שגם מקושרים אליהם מספרים, כמו למשל האוכלוסיות ומאפיינים נוספים של אזורים במפה, הגבהים של ילדים בבית הספר, או מספר המילים בכל פסקה במאמר הזה. נוכל לנתח נתונים מהסוג הזה באופן דומה לאופן שבו אנו חושבים על נקודות על גבי דף.
גילוי ''צורת'' הנתונים
תחום המחקר המשתמש בטופולוגיה על נתונים נקרא ניתוח נתונים טופולוגי (TDA) [5–3]. במסגרת תחום זה, אנו מנסים לתאר את הצורה של סֶט נתונים על ידי בניית סדרה של תמונות. על ידי חיבור ה''נקודות'' בסט נתונים במגוון דרכים, אנו יכולים לחקור את המבנה של הנתונים. במקום לחבר את הנקודות על ידי מתיחת קווים מנקודה אחת לאחרת כפי שאנו רגילים לעשות, אנו מחברים את הנקודות על ידי הגדלת גודלן. כשאנו מגדילים את הנקודות, הפערים בין הנקודות מצטמצמים, ובסופו של דבר הנקודות חופפות (ראו איור 3).
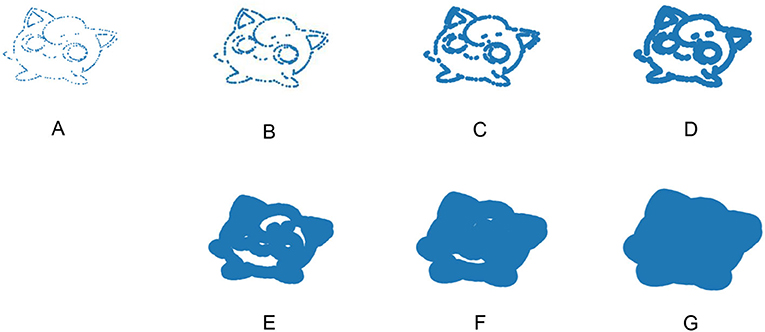
- איור 3 - ציור הפוקימון גִּ'יגְלִיפַּף באמצעות נקודות הולכות וגדלות.
- ב-(A–G), אנו מציירים את גִּ'יגְלִיפַּף באמצעות נקודות הולכות וגדלות. כאשר הנקודות קטנות, הן לא נוגעות זו בזו, ולכן ישנן הרבה פיסות ואין חורים. כשהנקודות גדלות, חלק מהן נוגעות זו בזו, ואז מספר הפיסות קטן ומתחילים להתפתח חורים. בהתחלה, קל יותר לראות את גִּ'יגְלִיפַּף כאשר הנקודות גדלות, אולם בהמשך נעשה קשה יותר לראותו. בטבלה 1, אנו מציינים את מספר הפיסות ומספר החורים בכל תמונה באיור הזה.
חשוב להבין באיזה גודל ליצור את הנקודות. מה אם נעשה את הנקודות ממש גדולות, כמו באיור 3G? אז יש לנו אובייקט אחד גדול מאוד, ללא חורים. בדוגמה הזו כאשר הנקודות גדולות מאוד, נעשה קשה להבחין בגִ'יגְלִיפַּף. אנו יכולים להבחין בדברים מעניינים עבור נקודות בגדלים שונים. על ידי שימוש במתמטיקה ובמחשוב, אנו יכולים לשקול גדלים רבּים של נקודות, ולקבל אובייקט לכל סדר גודל. לכל אחת משבע הגרסאות של גִּ'יגְלִיפַּף (באיור 3). יש מספר שונה של פיסות וחורים, שאותם אנו יכולים לספור (ראו טבלה 1).
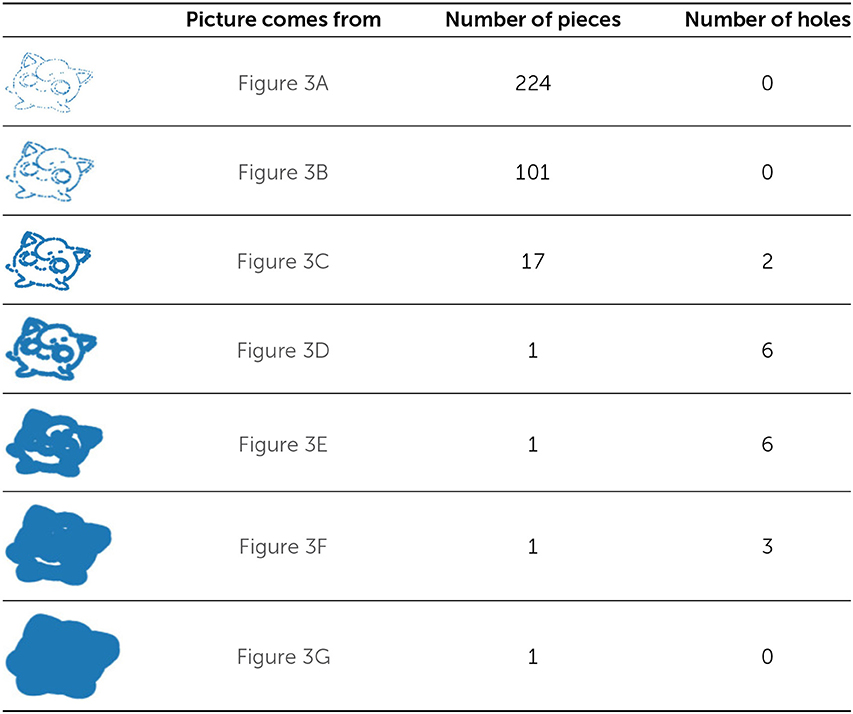
- טבלה 1 - אנו יכולים לתאר את שבע התמונות של גִּ'יגְלִיפַּף באיור 3 באמצעות זוגות המספרים הבאים: (224, 0), (101, 0), (17, 2), (1, 6), (1, 6), (1, 3) ו-(1, 0).
- בכל זוג מספרים, הערך הראשון מצביע על מספר הפיסות והערך השני על מספר החורים.
המידע בטבלה 1 הוא דרך לתיאור ולסיכום של מה שאנו רואים מחקירת טווח גדלי הנקודות– אנו חוקרים את המבנה של גִּ'יגְלִיפַּף בין גדלים רבים (כלומר, סקאלות). כל גרסה של גִּ'יגְלִיפַּף באיור 3 היא בסקאלה אחרת, ועל ידי ספירת מספר הפיסות ומספר החורים בכל סקאלה, אנו יכולים לחקור את טווח גדלי הנקודות שלגביהן המאפיינים של גִּ'יגְלִיפַּף ממשיכים להתקיים. זוהי גישה שכיחה בניתוח נתונים טופולוגי: אנו מתבוננים בגדלי הנקודות שבהם מאפיינים שונים ממשיכים להתקיים, בנתונים שאנו רוצים לחקור.
מה ניתן ללמוד מניתוח נתונים טופולוגי?
תחום מחקר זה יכול ללמד אותנו הרבה על דברים רבּים בעולם. הוא מאפשר לנו לחקור נתונים מורכבים במגוון נושאים עצום במדעי החברה, בביולוגיה, באסטרונומיה ועוד [3].
שימוש בניתוח נתונים טופולוגי יכול לסייע לנו להבין את היקום. כוכבי לכת כמו כדור הארץ הם חלק ממערכת השמש, שבתורה היא חלק מגלקסיות, שמתקיימות בצְבִירִים. אם אנו מסתכלים באמצעות טלסקופ ועושים ''זוּם'' אל תוך מערכת השמש, כוכבי הלכת נראים רחוקים מאוד זה מזה. אולם אם אנו מתרחקים ומסתכלים על הגלקסיה כולה, כל מערכת שמש יכולה להופיע פשוט בתור נקודה, ומבנים בתוך מערכת השמש נראים כמתמזגים יחד. אם נתרחק החוצה עוד יותר, כל גלקסיה עשויה להופיע בתור נקודה. במטרה לחקור את המבנה של היקום בסקאלות השונות האלה, מדענים השתמשו בניתוח נתונים טופולוגי על מנת לספור את הכמות של פיסות וחורים בסֶטים של נתונים על מיקומי כוכבים [6].
דוגמא נוספת, מדענים פנו לתחום מחקר זה במטרה לבחון את הדפוסים של עורקים בעלים [7]. הם חקרו את המבנה של יותר מ-100 עלים ומצאו בהם תבניות שונות – בדומה לטביעות אצבעות של בני אדם. טביעות האצבעות האלה יכולות לסייע בשיפור היכולת של מדענים לזהות עלים מפיסות עלים קטנות, ועשויות להועיל בשיפור הבנתנו את אופן גדילת העלים. ניתוח נתונים טופולוגי שימושי גם לחקירת המבנה של פטריות, כלי דם ודברים נוספים בעלי ענפים ולולאות.
חוקרים משתמשים בניתוח נתונים טופולוגי גם בכדי לתאר תבניות פעילוּת של אנשים ושל חיות. לדוגמה, שניים מאיתנו חקרו לאחרונה דפוסי הצבעה בבחירות באזורים שונים בקליפורניה [8]. השתמשנו בניתוח נתונים טופולוגי כדי לאתר אזורים במדינה שבהם אנשים הצביעו אחרת מאשר באזורים השכנים בבחירות לנשיאות בשנת 2016. גם חיות מייצרות תבניות מעניינות. להקות של דגים ושל ציפורים כוללות הרבה פרטים ויכולות ליצור מבנים יפהפיים. ניתוח נתונים טופולוגי יכול לסייע למדענים לחקור את התבניות המורכבות האלה ולהבינן [9].
לסיכום, ניתוח נתונים טופולוגי הוא גישה שנעשית פופולרית יותר ויותר לחקירת בעיות רבות, שנעות מחיבור בין נקודות בתמונות של פוקימון ועד למבנה של היקום [6], דפוסים בטבע [7], תבניות הצבעה גיאוגרפיות של בחירות [8], ועוד. זהו תחום מחקר מרתק וחשוב במתמטיקה שמסייע לאנשים למצוא היגיון בנתונים מורכבים [3–5].
מילון מונחים
טופולוגיה (Topology): ↑ ענף במתמטיקה המשמש במטרה לחקור את הצורות של אובייקטים.
זהוּת טופולוגית (Topologically Equivalent): ↑ מונח שמתאר שני אובייקטים שיכולים להפוך זה לזה על ידי מתיחתם, כיווצם, עיקומם, או עטיפתם (אולם לא על ידי הדבקתם או קריעתם).
וידיאו 1 (Video 1): ↑ טרנספורמציה של אותיות במילה ''פוקימון'' במטרה לשייכן לקבוצות של אותיות דומות. כל אחת מהקבוצות מכילה אותיות זהות טופולוגית.
נתונים (Data): ↑ מאפיינים ומידע, באופן טיפוסי בצורה של עובדות כמותיות ומאפיינים כמותיים אחרים, שנאספים דרך תצפיות או באופן אחר.
סֶט נתונים (Data Set): ↑ אוסף של נתונים. לעיתים קרובות ניתנת לחקירה באמצעות מחשב.
ניתוח נתונים טופולוגי (Topological Data Analysis - TDA): ↑ משפחת טכניקות לחקירת ה''צורה'' של נתונים באמצעות טופולוגיה.
סקאלה (Scale): ↑ גודל אופייני של אובייקט, כמו למשל הרדיוס של דיסק או אורך צלע ריבוע.
הצהרת ניגוד אינטרסים
המחברים מצהירים כי המחקר נערך בהעדר כל קשר מסחרי או פיננסי שיכול להתפרש כניגוד אינטרסים פוטנציאלי.
תודות
אנו מודים לקוראים הצעירים שלנו –Charlotte Amann-Sulzmann, Simon Cafiero, Addison Cart, Nia Chiou, Valerie K. Eng, Linnea Keiser-Clark, Coralea Lash-St. John, Adele Low, Maple Leung, Nora Stricker, Kate Van Hooser, ואדם אנונימי אחד – על הערותיהם הרבות והמועילות. אנו מודים גם להוריהם, למוריהם ולחבריהם – Clayton Cafiero, Lyndie Chiou, Puck Rombach ו- Hooser Steve Van, על שקישרו אותנו אליהם ועודדו את המשובים שלהם. אנו מבקשים להודות ל-Norman Redington, לעורכים שלנו ולסוקרים שלנו על הערות מועילות. MAP, MF ו- YHK מודים על התמיכה מהקרן הלאומית למדעים (מענק מספר 1922952) דרך תוכנית האלגוריתמים לאיתור אִיּוּם (ATD). CMT מודה על התמיכה מהקרן הלאומית למדעים (מענק מספר 1813752) דרך המחלקה למדעי המתמטיקה.
מקורות
[1] ↑ Ghrist, R. W. 2014. Elementary Applied Topology. Seattle, WA: Createspace. Available online at: https://www.math.upenn.edu/~ghrist/notes.html
[2] ↑ Stolz, B. J., and Mahler, B. I., 2015. ‘H’ is for homology. Available online at: https://www.maths.ox.ac.uk/about-us/life-oxford-mathematics/oxford-mathematics-alphabet/h-homology
[3] ↑ Otter, N., Porterm M. A., Tillmann, U., Grindrod, P., and Harrington, H. A. 2017. A roadmap for the computation of persistent homology. EPJ Data Sci. 6:17. doi: 10.1140/epjds/s13688-017-0109-5
[4] ↑ SIAM News. 2020. January/February 2020 issue. SIAM. 53. Available online at: https://sinews.siam.org/Current-Issue/Issue-Archives/Issue-Archives-ListView/PID/2282/mcat/2279/evl/0/TagID/302?TagName=Volume-53-|-Number-1-|-January%2FFebruary-2020
[5] ↑ Topaz, C. M. 2016. Topological data analysis: One applied mathematician’s heartwarming story of struggle, triumph, and (ultimately) more struggle. DSWeb: The Dynamical Systems Web. Available online at: https://dsweb.siam.org/The-Magazine/Article/topological-data-analysis
[6] ↑ Cisewski-Kehe, J., Wu, M., Fasy, B., Hellwing, W., Lovell, M., Rinaldo, A., et al. 2018. “Investigating the cosmic web with topological data analysis,” in American Astronomical Society Meeting Abstracts #231. Washington, DC. Available online at: https://ui.adsabs.harvard.edu/abs/2018AAS...23121307C/abstract
[7] ↑ Ronellenfitsch, H., Lasser, J., Daly, D. C., and Katifori, E. 2015. Topological phenotypes constitute a new dimension in the phenotypic space of leaf venation networks. PLoS Comput. Biol. 11:e1004680. doi: 10.1371/journal.pcbi.1004680
[8] ↑ Feng, M., and Porter, M. A. 2021. Persistent homology of geospatial data: A case study with voting. SIAM Rev. 63:67–99. doi: 10.1137/19M1241519
[9] ↑ Topaz, C. M., Zeigelmeier, L., and Halverson, T. 2015. Topological data analysis of biological aggregation models. PLoS ONE 10:e0126383. doi: 10.1371/journal.pone.0126383
