ملخص
يستخدم العلماء فرعًا من العلوم الرياضية يعرف باسم الطوبولوجيا لدراسة أشكال الأجسام. ويعد إحصاء عدد الأجزاء وعدد الفجوات في جسم ما من الأمور المهمة في الطوبولوجيا، حيث يستخدم العلماء هذه المعلومات لتصنيف هذه الأجسام في مجموعات من أنواع مختلفة. فعلى سبيل المثال، يوجد في الكعكة نفس عدد الفجوات ونفس عدد الأجزاء الموجودة في فنجان الشاي ذي اليد الواحدة، ولكنها تختلف عن الكرة. وفي الدراسات التي تشبه الأنشطة مثل ”توصيل النقاط“، يستخدم العلماء الأفكار المأخوذة من الطوبولوجيا لدراسة ”شكل“ البيانات. وقد استخدم العلماء الأفكار والطرق المأخوذة من الطوبولوجيا لدراسة الهياكل المتفرعة للعروق في أوراق النبات، والتصويت في الانتخابات، وأنماط الطيران في نماذج أسراب الطيور، والمزيد.
ما المقصود بالشكل؟
الأشكال مهمة جدًا لوجودنا؛ حتى إن مخ الإنسان يبدأ في ملاحظتها في الشهر الرابع أو الخامس من عمره. ولكن، ما الذي نعنيه بكلمة ”شكل” على وجه التحديد؟ اعتدنا على وصف أشكال شائعة مثل الخطوط والدوائر والمكعبات، ولكن ماذا عن الأجسام الأكثر تعقيدًا مثل التنين أو البوكيمون أو الإنسان؟
الطوبولوجيا فرع من الرياضيات يُعنى بدراسة أشكال الأشياء [1, 2]. وللمساعدة على فهم الطوبولوجيا، دعونا نتخيل أنه لدينا شريط مطاطي دائري، وأننا نريد وصف خصائص هذا الجسم الذي يبقى كما هو في حالات التمدد والانكماش والثني، ولكن بدون لصق الأشياء ببعضها البعض أو كسر الشيء وتمزيقه (أو عمل أي نقاط حادة فيه). من المنظور الطوبولوجي، يمكن أن نقول إن كلًا من الدائرة والشكل البيضاوي متكافئان طوبولوجيًا ؛ وذلك لأنه من الممكن أن نمدد الرباط ليأخذ الشكل البيضاوي. ومع ذلك، فلا يمكن القول إن هذا الشريط المطاطي متكافئ طوبولوجيًّا مع جزء من خيطٍ، لأن الشريط به فجوة في منتصفه، وهو ما لا يوجد في الخيط. تذكر أنه لا يجوز لنا أن نلصق أطراف الخيط ببعضها البعض، كما أنه لا يجوز أن نقطع الشريط المطاطي.
يمكننا، من خلال اكتشاف الأشكال المتكافئة مع بعضها البعض بهذه الطريقة الخاصة، أن نميز الأشكال ونصنفها في مجموعات مختلفة. على سبيل المثال، دعونا نصنف حروف كلمة Pokémon إلى مجموعات من أجسام متكافئة طوبولوجيًا. انظر الرسم المتحرك القصير في الفيديو 1. الحرفان “P” و“o” ينتميان إلى نفس المجموعة حيث يمكننا أن نضغط الجزء السفلي من الحرف “P” لأعلى ثم نوسع الفجوة لتصبح على شكل حرف “o”. وبالتالي، فإن كلًا من الحرف “P” وتكراري الحرف “o” يشكل مجموعة واحدة من الحروف المتكافئة طوبولوجيًا. بينما تُكوِّن الحروف “K” و“m” و“n” مجموعة أخرى، حيث يمكننا تحويل كل منها إلى نقطة من خلال ضغطها وثنيها. أما الحرف الأخير في الكلمة، وهو “é”، ففيه نوع من الإثارة والتشويق. فبدون علامة النبر التي عليه، يمكننا أن نقلص الذيل الدائري في “e” إلى الجانب الأيسر من شبه الدائرة على قمة الحرف. ثم يمكننا بعدها أن نمدد شبه الدائرة لنحصل على شكل الحرف “o”، وهو ما يضعه في نفس مجموعة الحرفين “P” و“o”. أما مع وجود علامة النبر عليها، يكون له جزءان، وحيث إنه لا يمكننا أن نلصق الجزءين سويًا، فإن هذا الحرف ينتمي إلى مجموعته الخاصة.
وتتشارك الأشكال التي تقع في نفس المجموعة بعض الخصائص المهمة عمومًا. فعلى الرغم من أن تفاصيل كل من الشكلين “P” و“o” مختلفة، إلا أنه يوجد بكليهما فجوة لا يمكن إزالتها. وفي المقابل، لا توجد هذه الفجوة في الحروف “k” و“M” و“n”. وإذا نظرنا إلى الحرف الكبير “B”، لوجدنا أنه لا ينتمي إلى أي من هاتين المجموعتين. ومع ذلك، فهو متكافئ طوبولوجيًا مع الرقم “8”، حيث توجد فجوتان بكليهما. إن عدد الأجزاء الموجودة في جسم ما مهم أيضًا، وعليه يكون حرف “é” (بفجوة واحدة وجزءين) منتميًا إلى مجموعة مختلفة عن غيرها من جميع الحروف التي ناقشناها. حاول تصنيف حروف اسمك إلى مجموعات من حروف متكافئة طوبولوجيًا.
دعونا الآن نجعل الأمور أكثر تشويقًا وإثارة للاهتمام من خلال النظر إلى عدد من البوكيمون نفسه. أحصِ عدد الأجزاء والفتحات في كل بوكيمون في الشكل 1. هل تستطيع أن تصنف أيًّا من هذه الأشكال في مجموعات بناء على هذه المعلومة؟

- شكل 1 - للبوكيمون أشكال مختلفة كما نرى في (A) Gastly، و (B) Haunter، و(C) Gengar.
- هل يمكنك أن تصنف البوكيمونات ذات الأشكال المختلفة في ضوء أعداد الفجوات وأعداد الأجزاء الموجودة فيها؟
قد يكون من الصعب دراسة طوبولوجيا الأجسام الصلبة مثل هذه التي ناقشناها في مقالنا حتى الآن، ولكننا نفكر في رسم صور في أنشطة مثل ”نشاط توصيل النقاط”. فلدينا مجموعة من النقاط التي نرى منها ما يكفي لتعطينا فكرة جيدة حول الشكل الذي سنحصل عليه عند توصيلها ببعضها (انظر الشكل 2). وعلى الرغم من أن الناس ماهرين في تكوين الأشكال من هذه النقاط، فإن السؤال هنا هو ”هل توجد طريقة لفعل هذا الأمر تلقائيًا؟” وعلى الرغم من أن هذا النوع من النشاط يمثل مهمة صعبة على الحاسوب مقارنة بما إذا قام به الإنسان، فإن علماء الرياضة وغيرهم من العلماء يبحثون عن طرق جيدة للقيام بهذا الأمر تلقائيًا لأننا نريد أن ننظر إلى مجموعات مختلفة من النقاط.

- شكل 2 - هل يمكنك أن تتخيل الشكل الذي سيكون عليه البوكيمون إذا وصلت النقاط ببعضها البعض؟ ستكون البوكيمونات التي نحصل عليها هي (A) Jigglypuff، و(B) Eevee، و(C) Butterfree.
تستطيع الطوبولوجيا مساعدتنا على فهم الكميات الضخمة من البيانات، ويمكننا حتى أن نستكشف طوبولوجيا تشكيلة من البيانات (تدعى مجموعة البيانات) في صورة لعبة عملاقة من ”توصيل النقاط”. في الحياة الحقيقية، هناك أنواع مختلفة وكثيرة من البيانات، علما بأن هذه البيانات قد لا تأتي في هيئة نقاط على الورق. ومع ذلك، فسنركز على البيانات التي ترتبط بالأرقام، مثل أعداد السكان وغيرها من خصائص المناطق السكانية على الخريطة، وأطوال الأطفال في المدارس، أو عدد الكلمات في كل فقرة من هذا المقال. يمكننا تحليل البيانات من هذا النوع بطريقة مشابهة لما نفكر فيه حول النقاط على صفحة ما.
اكتشاف شكل البيانات
يدرس الناس كلًا من الطوبولوجيا والبيانات سويًا في فرعٍ من العلوم يعرف باسم تحليل البيانات طوبولوجيًا (TDA) [5–3]. يحاول العلماء في هذا الفرع من العلوم وصف شكل مجموعة من البيانات من خلال بناء سلسلة من الصور. يمكننا من خلال توصيل ”النقاط” الموجودة في مجموعة بيانات بطرق متعددة أن ندرس هيكل هذه البيانات وتركيبها. وبدلًا من توصيل النقاط عن طريق رسم خطوط من نقطة لأخرى مثل ما اعتدنا فعله، فإننا نصل النقاط ببعضها من خلال زيادة حجمها. وبينما نزيد من حجم النقاط، يصغر حجم الفجوات التي بينها، ومن ثم تتداخل هذه النقاط فيما بينها في نهاية المطاف (انظر الشكل 3).
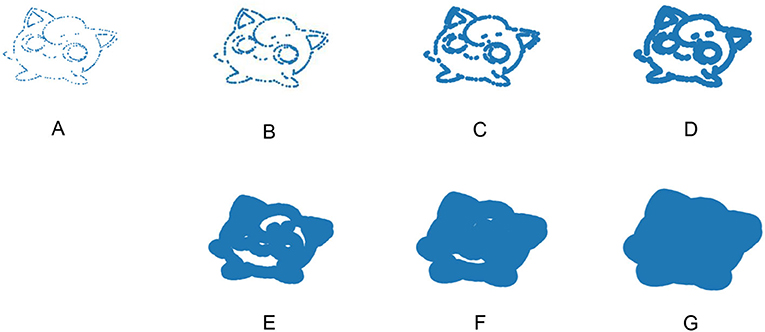
- شكل 3 - في (G - A)، يمكننا رسم Jigglypuff باستخدام النقاط الضخمة.
- عندما تكون النقاط صغيرة، فإنها لا تلمس بعضها البعض، وهو ما يعني وجود العديد من الأجزاء وغياب الفجوات. وعندما تصير النقاط أكبر في الحجم، فإن بعضها يلامس الآخر، ومن ثم تقل أعددا الأجزاء وتظهر بعض الفجوات. في البداية، يصبح من السهل رؤية Jigglypuff حيث إن النقاط تصبح أكبر حجمًا، ثم تصبح رؤيته بعد ذلك أصعب. ذكرنا في الجدول 1 عدد الأجزاء وعدد الفجوات في كل صورة في هذا الشكل.
من المهم أن نكتشف مدى الضخامة (كبر الحجم) الذي يجب أن نجعل عليه النقاط. ماذا لو جعلنا هذه النقاط ضخمة حقًا، كما في الشكل 3G؟ سنحصل حينها على جسم ضخم جدًا بلا فجوات. في هذا المثال، يصبح من الصعب جدًا تمييز Jigglypuff (شخصية من شخيصات البوكيمون) عندما تكون النقاط كبيرة جدًا. والمثير للاهتمام أنه ربما يمكننا ملاحظة أشياء شيقة عندما نغير من أحجام النقاط بشكل مختلف. يمكننا من خلال استخدام الرياضيات والحساب أن نحصل على العديد من الأحجام المختلفة للنقاط وأن نحصل على جسم مختلف من كل حجم. كل نسخة من النسخ السبع لـ Jigglypuff في الشكل 3 لها عدد مختلف من الأجزاء والفجوات، ويمكننا إحصاء ذلك (انظر الجدول 1).
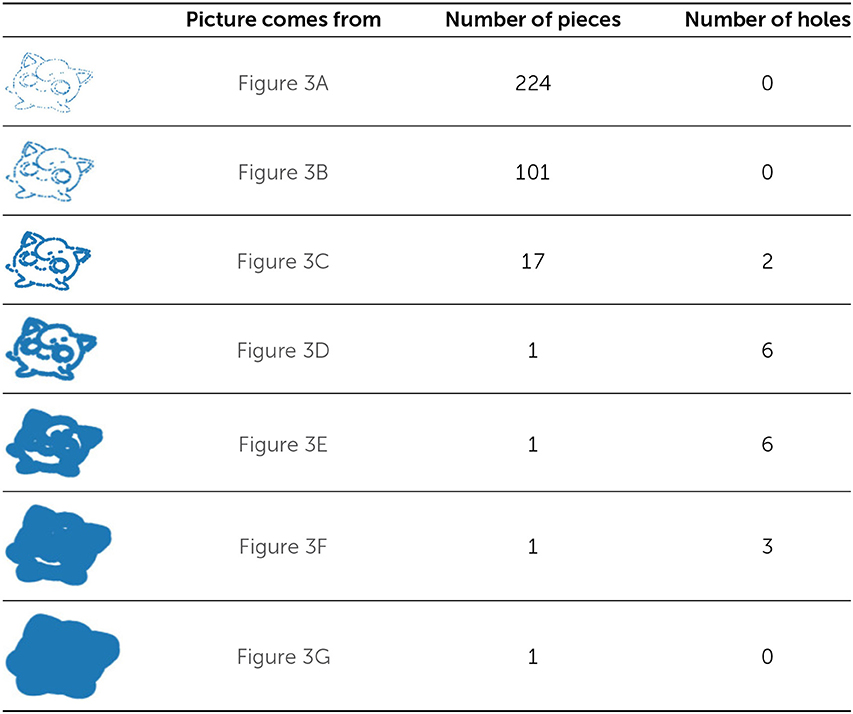
- جدول 1 - يمكننا وصف الصور السبع لـ Jigglypuff في الشكل 3 باستخدام الأزواج التالية من الأرقام: (224، 0) و(101، 0) و(17، 0) و(1، 6) و(1، 6) و(1، 3) و(1، 0).
- في كل زوج من هذه الأرقام، تشير القيمة الأولى إلى عدد الأجزاء بينما تشير القيمة الثانية إلى عدد الفجوات.
تعد المعلومات في الجدول 1 إحدى طرق وصف وتلخيص ما نلاحظه عند دراسة هذه المجموعة من أحجام النقاط. وهو ما يعني أننا ندرس تركيب Jigglypuff في أحجام عديدة (أي على مقاييس مختلفة). تقع كل نسخة من Jigglypuff في الشكل 3 على مقياس معين. ومن خلال إحصاء عدد الأجزاء وعدد الفجوات في كل مقياس، يمكننا استكشاف نطاق حجم النقاط التي تقوم عليها صفات Jigglypuff في الأساس. وهذا المنهج شائع في تحليل البيانات طوبولوجيًا، بمعنى أننا ندرس أحجام النقاط التي تثبت عليها الخصائص المختلفة في البيانات التي نريد دراستها.
ما الذي نتعلمه من تحليل البيانات طوبولوجيًا؟
يمكن لِتحليل البيانات طوبولوجيًا أن يخبرنا بالكثير من الأشياء حول هذا العالم. فهذه الطريقة تتيح لنا استكشاف مجموعة من البيانات المعقدة في مجموعة متنوعة من الموضوعات في العلوم الاجتماعية وعلم الأحياء وعلم الفلك وغيرها الكثير [3].
يمكننا استخدام تحليل البيانات طوبولوجيًا للمساعدة على فهم العالم من حولنا. تمثل الكواكب مثل الأرض جزء من نظامنا الشمسي، وهي تعتبر بدورها جزءًا من المجرات والتي تكون العناقيد السماوية. فلو نظرنا من خلال التليسكوب وكبرنا نظامنا الشمسي، لوجدنا أن الكواكب تبدو بعيدة جدًا عن بعضها البعض.
ولكن لو صغرنا نطاق عدسة التليسكوب لننظر إلى كل المجرة، فسيظهر كل نظام شمسي كنقطة واحدة، كما ستبدو تراكيب الأجسام في النظام الشمسي مندمجة مع بعضها البعض. ولو صغرنا العدسة أكثر، فقد تبدو كل مجرة وكأنها مجرد نقطة. ولدراسة تركيب الكون على هذه المقاييس المختلفة، استخدم العلماء تحليل البيانات طوبولوجيًا لإحصاء أعداد الأجزاء والفجوات في مجموعة بيانات مواقع النجوم [6].
وبالعودة مرة ثانية إلى الأرض، استخدم العلماء تحليل البيانات طوبولوجيًا لفحص أنماط العروق في أوراق النبات [7]، حيث درسوا تركيب أكثر من 100 ورقة ليكتشفوا أنماطًا مختلفة فيه؛ مثل بصمات الأصابع في الإنسان. ويمكن لبصمات الأصابع هذه أن تساعد في تعزيز قدرة العلماء على التعرف على الأوراق وتمييزها من قطع الورق الصغيرة، كما قد تكون مفيدة في تعزيز فهمنا حول كيفية نمو الأوراق. وتحليل البيانات طوبولوجيًا مهم أيضًا لدراسة تركيب الفطريات والأوعية الدموية وغيرها من الأشياء ذات الفروع والعقد.
كما يستخدم الناس أيضا تحليل البيانات طوبولوجيًا لوصف أنماط الأنشطة التي يؤديها البشر والحيوانات. على سبيل المثال، درس اثنان منا مؤخرًا أنماط التصويت الجيوغرافي في مناطق مختلفة من ولاية كاليفورنيا الأمريكية [8]، حيث استخدما تحليل البيانات طوبولوجيًا لاكتشاف المناطق في الولاية التي صوت الناس فيها على نحوٍ مختلف عن غيرهم في المناطق المجاورة في الانتخابات الرئاسية لعام 2016. وبالإضافة إلى البشر، تنتج الحيوانات أنماطًا مثيرة للاهتمام. فأسراب الأسماك وأسراب الطيور تضم العديد من الأفراد، ومن ثم تستطيع أن تشكل تراكيب جميلة. يمكن لتحليل البيانات طوبولوجيًا مساعدة العلماء على اكتشاف هذه الأنماط المعقدة وفهمها [9].
وإيجازًا، يعد تحليل البيانات طوبولوجيًا منهجًا آخذًا في الذيوع والانتشار في دراسة العديد من المسائل التي تتنوع من توصيل النقاط في صور البوكيمون إلى بنية الكون وتركيبه [6]، والأنماط الموجودة في الطبيعة [7]، وأنماط التصويت الجيوغرافي في الانتخابات [8]، وأكثر من ذلك بكثير. يمثل تحليل البيانات طوبولوجيًا منطقة مذهلة ومهمة في علم الرياضيات الذي يساعد الناس على فهم البيانات المعقدة [3–5].
مسرد للمصطلحات
الطوبولوجيا (Topology): ↑ فرع من علم الرياضيات يستخدمه العلماء لدراسة أشكال الأجسام.
متكافئ طوبولوجيًا (Topologically Equivalent): ↑ مصطلح يستخدم للدلالة على وجود جسمين يمكن تحويل أحدهما للآخر من خلال التمدد أو الانكماش أو الثني أو اللف (ولكن ليس من خلال لصقهما ببعضهما البعض أو تمزيقهما).
الفيديو 1: ↑ تحويل الحروف في كلمة ”بوكيمون” لتصنيفها في مجموعات من حروف متشابهة. تتكون كل مجموعة من حروف متكافئة طوبولوجيًا.
البيانات (Data): ↑ هي الخصائص والمعلومات التي عادة ما تكون في شكل حقائق كميّة وغيرها من السمات الكمية والتي تجمع من خلال عمليات المشاهدة أو غيرها من الطرق.
مجموعة البيانات (Data Set): ↑ تشكيلة من البيانات. تكون مجموعة البيانات عادة في صيغة يمكن دراستها باستخدام الحاسب الآلي.
تحليل البيانات طوبولوجيًا (Topological Data Analysis): ↑ مجموعة من التقنيات تستخدم في دراسة ”شكل” البيانات باستخدام الطوبولوجيا.
المقياس (Scale): ↑ الحجم الخاص لجسم ما مثل نصف قطر الأسطوانة أو طول ضلع في مربع.
إقرار تضارب المصالح
يعلن المؤلفون أن البحث قد أُجري في غياب أي علاقات تجارية أو مالية يمكن تفسيرها على أنها تضارب محتمل في المصالح.
شكر وتقدير
نعرب عن امتناننا للقراء الصغار: Charlotte Amann-Sulzmann، وSimon Cafiero، وAddison Cart، وNia Chiou، وValerie K. Eng، وLinnea Keiser-Clark، وCoralea Lash-St. John، وAdele Low، وMaple Leung، وNora Stricker، وKate Van Hooser، وشخص آخر مجهول الهوية - لتعليقاتهم المفيدة على هذا الموضوع. كما نشكر أيضا آبائهم ومدرسيهم وأصدقائهم - Clayton Cafiero، وLyndie Chiou، وPuck Rombach، وSteve Van Hooser - على إيصالنا بهم وطلب آرائهم. كما نتقدم بالشكر لـ Norman Redington، ومحررينا ومراجعينا على تعليقاتهم المفيدة. كما تقدَّر MAP وMF وYHK الدعم من the National Science Foundation (رقم المنحة 1922952) من خلال برنامج (Algorithms for Threat Detection (ATD) كما تقدَّر CMT الدعم من the National Science Foundation (رقم المنحة 1813752) من خلال برنامج the Division of Mathematical Sciences.
المراجع
[1] ↑ Ghrist, R. W. 2014. Elementary Applied Topology. Seattle, WA: Createspace. Available online at: https://www.math.upenn.edu/~ghrist/notes.html
[2] ↑ Stolz, B. J., and Mahler, B. I., 2015. ‘H’ is for homology. Available online at: https://www.maths.ox.ac.uk/about-us/life-oxford-mathematics/oxford-mathematics-alphabet/h-homology
[3] ↑ Otter, N., Porterm M. A., Tillmann, U., Grindrod, P., and Harrington, H. A. 2017. A roadmap for the computation of persistent homology. EPJ Data Sci. 6:17. doi: 10.1140/epjds/s13688-017-0109-5
[4] ↑ SIAM News. 2020. January/February 2020 issue. SIAM. 53. Available online at: https://sinews.siam.org/Current-Issue/Issue-Archives/Issue-Archives-ListView/PID/2282/mcat/2279/evl/0/TagID/302?TagName=Volume-53-|-Number-1-|-January%2FFebruary-2020
[5] ↑ Topaz, C. M. 2016. Topological data analysis: One applied mathematician’s heartwarming story of struggle, triumph, and (ultimately) more struggle. DSWeb: The Dynamical Systems Web. Available online at: https://dsweb.siam.org/The-Magazine/Article/topological-data-analysis
[6] ↑ Cisewski-Kehe, J., Wu, M., Fasy, B., Hellwing, W., Lovell, M., Rinaldo, A., et al. 2018. “Investigating the cosmic web with topological data analysis,” in American Astronomical Society Meeting Abstracts #231. Washington, DC. Available online at: https://ui.adsabs.harvard.edu/abs/2018AAS...23121307C/abstract
[7] ↑ Ronellenfitsch, H., Lasser, J., Daly, D. C., and Katifori, E. 2015. Topological phenotypes constitute a new dimension in the phenotypic space of leaf venation networks. PLoS Comput. Biol. 11:e1004680. doi: 10.1371/journal.pcbi.1004680
[8] ↑ Feng, M., and Porter, M. A. 2021. Persistent homology of geospatial data: A case study with voting. SIAM Rev. 63:67–99. doi: 10.1137/19M1241519
[9] ↑ Topaz, C. M., Zeigelmeier, L., and Halverson, T. 2015. Topological data analysis of biological aggregation models. PLoS ONE 10:e0126383. doi: 10.1371/journal.pone.0126383
