ملخص
أظهرت الدراسات أن الشخص العادي يطرح 20 سؤالًا بشكل يومي، وبطبيعة الحال، بعض من هذه الأسئلة يكون بسيطًا مثل أن تسأل معلمك إذا كان بإمكانك الذهاب إلى الحمام، ولكن بعضًا من هذه الأسئلة تأخذ شكلًا أكثر تعقيدًا وصعوبةً بحيث لا يسهل العثور على إجابة لها. ومن هذا المنطلق يأتي دور علم الإحصاء حيث يتيح لنا استخلاص استنتاجات من مجموعة بيانات وغالبًا ما يُطلق عليه مصطلح ”علم البيانات“، كما أنه يساعد الأفراد في كل مجال في العثور على إجابات على الأسئلة البحثية أو تلك المتعلقة بالعمل، ويساعد على التنبؤ بالنتائج مثلما يظهر لك تطبيق عرض الفيديوهات المفضل لديك المقطع الذي قد ترغب في مشاهدته لاحقًا. وبالنسبة لعلماء الاجتماع كما هو الحال مع علماء النفس، فإن علم الإحصاء يعد أداة تساعدهم في تحليل البيانات والإجابة على الأسئلة البحثية التي نطرحها.
طرح الأسئلة البحثية
يطرح العلماء مجموعة من الأسئلة التي يمكن الإجابة عنها بالاستعانة بعلم الإحصاء، فعلى سبيل المثال، قد يهتم باحث في علم النفس بدراسة كيفية تأثر أداء الطالب في الامتحان بعدد ساعات النوم التي يحصل عليها قبل ليلة الامتحان. هذا ويهتم علماء النفس وعلماء الأحياء والعديد من العلماء الآخرون بالإجابة عن الأسئلة المتعلقة بجماعة معينة أو بمجموعة من الأفراد، فعلى سبيل المثال، قد يهتم عالم الأحياء بدراسة نوع معين من الطيور بوصفها مجموعة خاضعة للبحث، أما عالم النفس التنموي فقد يهتم بإجراء أبحاث على الأطفال الذين تتراوح أعمارهم بين 3-6 سنوات، أما عالم الأمراض السريرية فقد يهتم بالمرضى المصابين بنوع معين من الأمراض. يعتمد نوع التحليل الإحصائي الذي يجب إجراؤه على السؤال المطروح والمتغيرات التي يتم قياسها، فالمتغيرات هي العوامل أو السمات أو الحالات التي تأخذ أشكالًا أو مقادير مختلفة مثل الطول أو العمر أو درجة الحرارة.
أخذ عينة من مجموعة
عند الإجابة على الأسئلة البحثية التي نطرحها، لا يمكن في الكثير من الأحيان أن نجمع معلومات من جميع أفراد المجموعة التي نهتم بدراستها، فعلى سبيل المثال، عند البحث في مسألة تأثير النوم على أداء الطالب في الامتحان، لا يمكننا جمع المعلومات المتعلقة بعدد ساعات نوم كل طالب في العالم والنتائج التي يحرزها في الامتحان، ولهذا السبب نجمع بيانات من عينة معينة من الأفراد التي تمثل المجموعة كلها على النحو الأمثل. ومن المهم أن تتشابه خصائص هذه العينة مع خصائص المجموعة ككل. حيث يحرص علماء الاجتماع على أن تكون العينات التي يدرسونها من نفس الفئة العمرية أو المجموعة العرقية تمثل المجموعة بأكملها. فإذا لم نحرص على أن تكون العينات متشابهة في خصائصها مع خصائص المجموعة بأكملها، فسيكون من الصعب الإجابة عن الأسئلة البحثية التي نطرحها (الشكل 1).
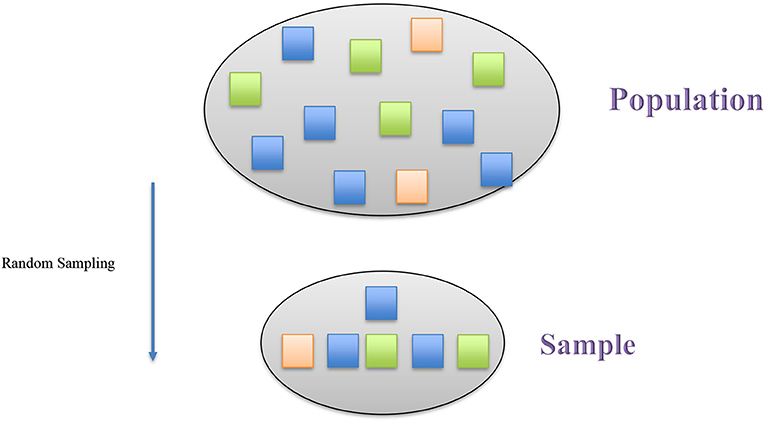
- شكل 1 - إن أخذ العينة العشوائية هو إحدى الطرق التي يمكن من خلالها اختيار العينة التي تمثل المجموعة بدقة.
- وعند أخذ عينة عشوائية، يكون لكل فرد من أفراد المجموعة فرصة متساوية ليتم اختياره للمشاركة في هذه العينة. ففي هذا المثال، نجد أن كل لون موجود في الشكل الذي يشير إلى المجموعة مُمثل في العينة، وينطبق ذلك أيضًا على نسبة كل لون.
فعلى سبيل المثال، لنفترض أنه توجد طبيبة بيطرية مهتمة بحساب متوسط وزن جميع الكلاب، فإنها ستجمع عينة من خمسة كلاب لتزنها، وستعرف حينها متوسط وزن عينتها وستستنتج أن متوسط وزن جميع الكلاب يتراوح بين 10 و15 رطلًا. وإذا كنت من محبي الكلاب، فقد تشك أنه يوجد خطأ ما في هذا الرقم. فبعض الكلاب تكون كبيرة الحجم نوعًا ما، لذا فقد تتوقع أن يكون المتوسط أعلى من ذلك. فما الذي سيحدث إذا جمعت الطبيبة البيطرية هذه العينة فقط من مجموعة كلاب من سلالة الشيواوا؟ في هذه الحالة من المؤكد أنه لا يمكننا القول إن جميع الكلاب تزن حوالي 10 إلى 15 رطلًا. حيث إن العينة تقتصر على سلالة واحدة ليس إلا ولم تضم جميع أنواع الكلاب، فإذا جمعت الطبيبة البيطرية عينة تمثل جميع سلالات الكلاب، فمن المرجح أن يكون متوسط الوزن الذي قامت بقياسه من العينة مختلفًا تمامًا عن الرقم السابق.
تُعرف الطريقة الرئيسية لاختيار الأفراد المشاركين في عينة محددة لتمثيل مجموعة ما على النحو الأمثل باسم أخذ عينة عشوائية ويستخدم العلماء هذه الطريقة لضمان أن احتمال اختيار كل فرد من أفراد المجموعة يكون متساويًا، وهذا يضمن أن تكون العينة أكثر تشابهًا مع المجموعة بأكملها.
تقدير النتائج بناءً على العينة
بمجرد أن يجمع العالم العينة، قد يرغب في الحصول على استنتاجات حول تلك العينة وتعميم النتائج على المجموعة ككل. فعلى سبيل المثال، قد يرغب العالم في معرفة متوسط عدد ساعات نوم الأطفال الذين يبلغ عمرهم 12 عامًا كل ليلة أو متوسط طول طلاب المدارس الثانوية في الولايات المتحدة، ولتقدير قيمة المتغير في مجموعة معينة (مثل متوسط الطول)، يحسب العلماء نقطة التقدير من العينة. وتُعرف نقطة التقدير بأنها الرقم المسؤول عن تقدير القيمة الحقيقية للمتغير في المجموعة، وعادة ما تعبر نقطة التقدير عن المتوسط، فعلى سبيل المثال إذا أردنا معرفة متوسط عدد الأطفال في كل أسرة في مدينة شيكاغو، فسنجمع عينة عشوائية من الأسر في شيكاغو، وسنسأل كل أسرة عن عدد الأطفال الذين يعيشون في المنزل، وبعد ذلك، يمكننا حساب متوسط عدد الأطفال الذين يسكنون في هذه المنازل - باستخدام تلك المعلومات - لحساب نقطة التقدير، ثم يمكننا بعد ذلك افتراض أن متوسط عدد الأطفال في العينة الخاصة بنا يشبه إلى حد كبير متوسط عدد الأطفال الموجودين في جميع أسر شيكاغو (الشكل 2).

- شكل 2 - بدلًا من الذهاب إلى كل منزل في شيكاغو لمعرفة متوسط عدد الأطفال في كل منزل، يمكن للعلماء أخذ عينة.
- وفي هذا المثال، نجد أنه تم حساب عدد الأطفال الموجودين في كل أسرة في العينة، وتم حساب متوسط العينة، ووجد العالم أن كل أسرة في شيكاغو لديها طفلين في المتوسط، وهو ما يُعرف باسم نقطة التقدير.
وعلى كل، فلا يمكننا أن نصف هذه القياسات وطرق أخذ العينات بالدقة المتناهية، لذلك غالبًا ما يستخدم العلماء مجالات الثقة حول نقاط التقدير لإظهار مجموعة من القيم التي من المحتمل أن تحتوي على المتوسط الحقيقي للمتغير في المجموعة، ولحساب مجال الثقة، يجب على العالم أن يحسب هامش الخطأ في البداية، ويُعرف هامش الخطأ بأنه المقدار المحسوب الذي يُضاف إلى نقطة التقدير ويُطرح منها، فهو بمثابة طريقة تعبر عن الحسابات الخاطئة أو الأخطاء المحتملة من الناحية العددية في أخذ العينات من المجموعة (كما هو الحال عندما لا تمثل العينة المجموعة بالكامل).
لنتمرن على طريقة حساب مجال الثقة، تخيل أننا نجمع عينة من 49 طالبًا لإجراء دراسة عن النوم، ونجد أن متوسط عدد ساعات النوم للطلاب هو 10 ساعات ونصف (نقطة التقدير التي توصلنا إليها)، بعد ذلك، نحتاج إلى معرفة الانحراف القياسي وهو متوسط المسافة بين نقطة بيانات كل شخص ومتوسط الإجمالي. عندما تكون قيمة الانحراف القياسي صغيرة، فهذا يعني أن قيمة معظم البيانات قريبة من المتوسط، أما الانحراف القياسي ذو القيمة الكبيرة فيدل على أن البيانات موزعة على قيم كثيرة. وبالنسبة للعينة التي أخذناها، لنفترض أن الانحراف القياسي يبلغ ساعة ونصف، علينا أن نحسب هامش الخطأ باستخدام هذه المعادلة:

في هذه المعادلة ترمز ا إلى الانحراف القياسي (ساعة ونصف)، أما ع فتشير إلى عدد نقاط البيانات في العينة التي أخذناها (49 فردًا)، ومن ثم نستبدل هذين الرمزين بالقيمتين المكافئتين لهما. ونحسب هامش الخطأ ليبلغ 0.42 ساعة من النوم، ولاستكمال مجال الثقة، نضيف هامش الخطأ إلى نقطة التقدير التي توصلنا إليها ونطرحه منها لنحصل على الحد الأقصى والأدنى لمجال الثقة. وعادة ما يستخدم العلماء مجال ثقة قدره 95% لحساب هامش الخطأ مما يعني أنه يمكننا أن نكون واثقين أن مجال الثقة الذي توصلنا إليه - في 95% من المرات - يحتوي على المتوسط الفعلي للمجموعة، وعليه، فإن مجال الثقة لنقطة التقدير الواردة في المثال الذي طرحناه قد يبلغ 10.5 ± 0.42 ساعة أو 10.08 و 10.92، وهذا يعني أنه في 95% من المرات يكون عدد ساعات النوم الذي يحصل عليها الطلاب في المجموعة بأكملها يتراوح بين 10.08 و 10.92 ساعة (الشكل 3).
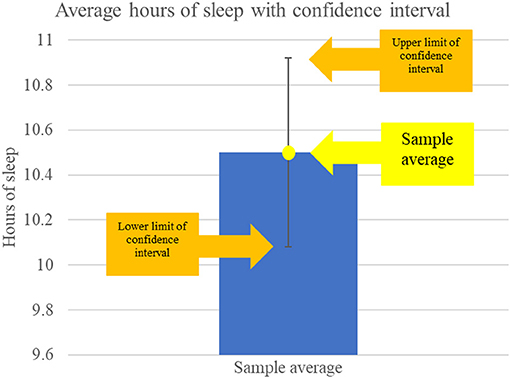
- شكل 3 - تظهر لنا مجالات الثقة مجموعة من القيم التي من المحتمل أن تحتوي على القيمة الحقيقية للمتغير في المجموعة.
- يوضح هذا المثال متوسط عدد ساعات النوم في العينة التي أخذناها (10.5 ساعة)، ويبين هذا العمود مجال الثقة 95% حول المتوسط، مع إضافة 0.42 ساعة من النوم إلى المتوسط ونطرحه منه للحصول على هامش الخطأ، ويوضح مجال الثقة أن المتوسط الحقيقي لعدد ساعات نوم الطلاب في المجموعة بأكملها يتراوح بين 10.08 و 10.92 ساعة.
يمكن للعلماء تقليل قيمة هامش الخطأ بشتى الطرق لجعل تقديراتهم المتعلقة بالمجموعة أكثر دقة، ومن بين هذه الطرق زيادة عدد الأفراد المشاركين في العينة حتى تمثل العينة المجموعة على أكمل وجه، أما الطريقة الأخرى لتقليل هامش الخطأ فهي التأكد من أن عملية جمع البيانات خالية من الأخطاء قدر الإمكان للحد من التباين في البيانات، مثل التأكد من أن جميع أدوات القياس (مثل المقاييس والاستطلاعات ووسائل القياس وما إلى ذلك) دقيقة في عملها، فكلما كانت العينة تمثل السكان بشكل أكثر دقة - من خلال استخدام العينات العشوائية وممارسات جمع البيانات الجيدة - قل هامش الخطأ وزادت دقة مجال الثقة في تقدير القيمة الحقيقية للمجموعة.
طرح أسئلة بحثية أكثر تعقيدًا
يرغب العلماء في بعض الأحيان في المبالغة في وصف الحسابات البسيطة مثل متوسط الطول أو العمر في المجموعات التي يدرسونها في سبيل فهم جوانب أكثر تعقيدًا لهذه المجموعات. لنقل إن اهتمامنا لا يقتصر على عدد ساعات النوم التي يحصل عليها الطلاب فحسب، بل يمتد ليشمل مقدار انخفاض درجات الاختبار بعد الحصول على قسط غير كافٍ من النوم. هذا ويعبر حجم الأثر عن القيم التي تقدر حجم الظاهرة أو الدرجة التي يؤثر بها متغير واحد (مثل ساعات النوم) على متغير آخر (مثل درجات الاختبار)، فعلى سبيل المثال، إذا كان حصولك على 3 ساعات فقط من النوم يجعلك تفقد بضع نقاط من درجات الاختبار الذي تؤديه، مقارنةً بحصولك على 9 ساعات من النوم، فقد لا "تشعر بالقلق" حيال قلة النوم. في حين أنه يوجد اختلاف في نتيجة الاختبار وهو لا يشكل فارقًا كبيرًا. مع ذلك، إذا فقدت الكثير من الدرجات التي ستحصل عليها في الاختبار بعد أن خسرت ٦ ساعات من نومك، فقد يؤثر ذلك على مجموعك ودرجاتك تأثيرًا كبيرًا. في هذه الحالة، من المحتمل أن توافق على أن قلة النوم لها عظيم الأثر على درجاتك.
وثمة طرق مختلفة لحساب حجم الأثر استنادًا إلى السؤال البحثي ونوع الإحصائيات التي يستخدمها العالم. فبمجرد أن يحسب العالم حجم الأثر، يمكنه تحديد ما إذا كان هذا الأثر صغيرًا أم متوسطًا أم كبيرًا، ويتيح حجم الأثر للعالم - وكذلك الأشخاص الآخرين الذين يراجعون النتائج - إدراك الأثر الذي تحدثه متغيرات معينة على متغيرات أخرى في المجموعة على نحو أفضل.
الخلاصة
يطرح العلماء العديد من الأسئلة المختلفة، ويمكن لعلم الإحصاء الإجابة عن هذه الأسئلة بعدة طرق، وتُعد الأمثلة الإحصائية التي طرحناها في هذا المقال بمثابة الطرق التي يمكن لعلماء الاجتماع من خلالها الإجابة عن هذه الأسئلة البسيطة عن طريق العينات، ولكن لا يقتصر علم الإحصاء على مجال بعينه أو على أحد ميادين البحث العلمي فقط، فقد ساعد علم الإحصاء العلماء على معرفة مدى احتمالية علاج بعض الأمراض، وساعد المهندسين في إدراك عوامل سلامة المركبة التي تقودها، ولا يتوقف دوره عند هذا الحد حيث إنه توجد أسئلة لا حصر لها يمكننا الإجابة عنها باستخدام علم الإحصاء.
مسرد للمصطلحات
المتغير (Variable): ↑ هو العامل أو السمة أو الحالة الذي يأخذ أشكالًا أو مقادير مختلفة تُقاس في البحث.
المجموعة (Population): ↑ هي عدد محدد من الأفراد الذين يرغب العلماء في الإجابة عن الأسئلة التي تدور حولهم.
أخذ عينة عشوائية (Random sampling): ↑ هي طريقة لاختيار الأفراد من بين مجموعة معينة بحيث تضمن أن يحصل كل فرد على احتمالية متساوية ليتم اختياره.
نقاط التقدير (Point estimate): ↑ هي تقدير لقيمة ما في مجموعة معينة مثل المتوسط.
مجالات الثقة (Confidence intervals): ↑ مجموعة من القيم حول نقاط التقدير التي من المحتمل أن تحتوي على القيمة الحقيقية لمتغير ما في المجموعة.
هامش الخطأ (Margin of error): ↑ هو المقدار المحسوب المضاف إلى نقاط التقدير والمطروح منها الذي يؤخذ في الاعتبار لإدراك الحسابات الخاطئة أو احتمالات الأخطاء.
الانحراف القياسي (Standard deviation): ↑ هو متوسط المسافة بين كل نقطة بيانات ومتوسط الإجمالي.
حجم الأثر (Effect size): ↑ يوضح لنا مدى الاختلاف الواقع بين القيم المتوسطة للمتغيرات.
إقرار تضارب المصالح
يعلن المؤلفون أن البحث قد أُجري في غياب أي علاقات تجارية أو مالية يمكن تفسيرها على أنها تضارب محتمل في المصالح.
مراجع إضافية للقراءة عن هذا الموضوع
Cumming, G. 2013. Understanding the New Statistics: Effect Sizes, Confidence Intervals, and Meta-Analysis. New York, NY: Routledge.
