ملخص
تخيَّل أنك ذاهب إلى المدرسة ووصلت إلى محطة الحافلات، فكم من الوقت عليك أن تنتظر قبل أن تصل الحافلة القادمة؟ المثير في الأمر أن عليك الانتظار لمدة أطول - في الغالب أطول بكثير- مما قد تتوقعه حين تنظر إلى جدول الحافلات، وهذه الظاهرة التي يطلق عليها مفارقة وقت الانتظار، ترجع جذورها في حقيقة الأمر إلى علم الرياضيات. ونستكشف في هذا المقال مفارقة وقت الانتظار، ونشرح أسباب حدوثها ونناقش بعضًا من تأثيراتها (بعيدًا عن احتمالية التأخُّر على المدرسة).
كم من الوقت عليك أن تنتظر قبل أن تصل الحافلة القادمة؟
تخيَّل أنك تعيش في مدينة وتستقل الحافلة للذهاب إلى المدرسة، ولأن الحافلات تمر بشكل مستمر على الحي الذي تسكنه، ربما لا تحتاج لمراجعة جدول الحافلات بشكل دقيق، ربما لا تحتاج إلا للذهاب إلى أقرب محطة حافلات وتستقل الحافلة القادمة (انظر الشكل 1A)، ولكن، إذا وصلت وليس لديك فكرة عن موعد وصول الحافلة القادمة، فكم من الوقت عليك الانتظار حتى تصل الحافلة القادمة؟
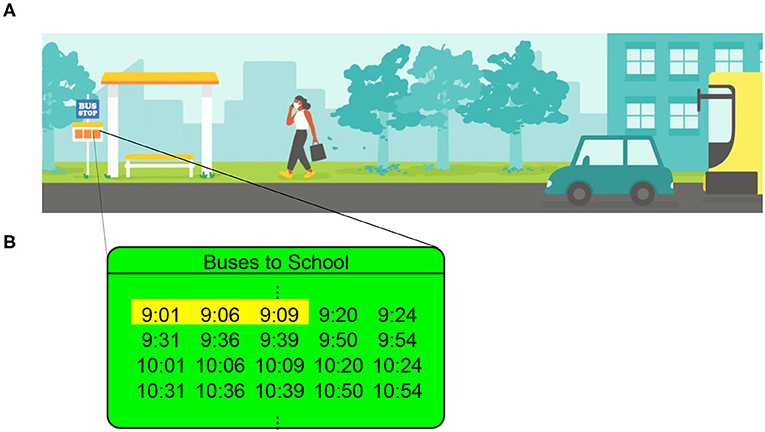
- شكل 1 - (A) تصل إلى محطة الحافلات وتنتظر الحافلة القادمة.
- (B) تراجع الجدول لتعرف أن هناك 10 حافلات تمر كل ساعة، مما يعني أن هناك حافلةً كل 6 دقائق. ومن المقرر أن تصل الحافلات الثلاث الأولى بعد الساعة 09:00 في تمام الساعات 09:01 و09:06 و09:09، ونقوم بالإشارة إلى هذه التوقيتات الثلاثة باللون الأصفر، وتبلغ المدة بين الحافلات المتعاقبة 5 دقائق (بين الحافلة الأولى والحافلة الثانية) و3 دقائق (بين الحافلة الثانية والحافلة الثالثة)، [رسمت اللوحة A من قبل Iris Leung.]
فلنفترض أن هناك 10 حافلات كل ساعة (انظر الشكل 1B)، ما يعني أن هناك حافلة كل 6 دقائق في المتوسط، إذا غادرت الحافلة الأخيرة قبل وصولك مباشرة، فعليك الانتظار لمدة 5 أو 6 دقائق حتى وصول الحافلة القادمة، وإذا غادرت الحافلة الأخيرة قبل وصولك ببضع دقائق، فربما عليك الانتظار دقيقة واحدة فقط حتى وصول الحافلة القادمة، أو ربما 4 دقائق أو دقيقتين؟ والتخمين المدروس لـ “وقت انتظارك” هو 3 دقائق، وهو نصف المدة بين الحافلات المتعاقبة تقريبًا، إلا أن هذا المنطق غير صحيح؛ إذ أن عليك الانتظار أكثر من 3 دقائق، وربما تكون مدة الانتظار أطول من 6 دقائق، ويطلق على هذه الظاهرة مفارقة وقت الانتظار [1, 2]، والمفارقة هي أمر يبدو وكأنه غير مفهوم أو منطقي، ولكن يتضح أنه حقيقة في نهاية الأمر. إذ يعتقد الكثير من الناس أن مفارقة وقت الانتظار مفارقة، لأن وقت الانتظار في محطة الحافلات يفوق نصف المدة بين مرور الحافلات (وهي 3 دقائق في المثال أعلاه)، وفي حقيقة الأمر؛ فإن مفارقة وقت الانتظار هي ظاهرة رياضية وليس لها علاقة بالحافلات، ولكن ما هي هذه الظاهرة وماذا تفعل لتضليلنا؟ استمر في قراءة المقال لتكتشف!
لماذا تحدث مفارقة وقت الانتظار؟
لنفهم لماذا تحدث مفارقة وقت الانتظار، علينا أن نسترجع جدول الحافلات في الشكل 2A، وهذا الجدول الذي يعتبر أبسط من الجدول الوارد في الشكل 1. تصل الحافلات إما كل 4 دقائق أو كل 12 دقيقة. ويحتوي جدول الحافلات الأصلي الوارد في الشكل 1B، على الكثير من الأرقام غير المنتظمة، وهناك العديد من الأوقات المختلفة بين الحافلات، وبصورة عامة عندما يبدو موقف ما معقدًا، فمن الأفضل دائمًا تبسيطه قبل تطبيق المنطق الرياضي عليه. يقوم الأشخاص الذين يعملون في مجال الرياضيات بهذا الأمر طوال الوقت، ومفارقة وقت الانتظار تحدث أيضًا في جدول الحافلات المبسط، وتفيد عملية التبسيط في تيسير فهم ما يحدث بطريقة أفضل.
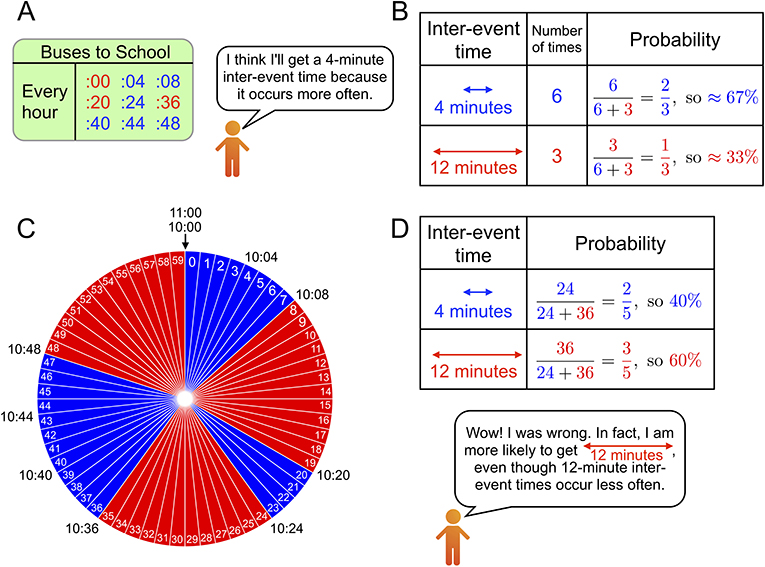
- شكل 2 - مقارنة بين التخمين الساذج لمتوسط وقت الانتظار ومتوسط وقت الانتظار الحقيقي.
- (A) جدول حافلات مبسط. (B) التخمين الساذج لاحتماليات الانتظار لمدة 4 دقائق و12 دقيقة بين الحافلات. ويعد هذا التخمين مبنيًا على فكرة خاطئة مفادها أن احتمالية أن يكون وقت الانتظار بين الحافلات 4 دقائق، أعلى من أن يكون 12 دقيقة، لأن هذا ما يتكرر أكثر، (C) توضيح أوقات الانتظار بين الحافلات التي تمر في ساعة واحدة في مخطط دائري، يمكنه أن يساعدنا في فهم سبب عدم دقة هذا التخمين. (D) إن الاحتمالية الواقعية للانتظار لمدة 12 دقيقة بين الحافلات، أكبر من احتمالية الانتظار لمدة 4 دقائق، لأن هناك 36 شريحة حمراء، بينما توجد 24 شريحة زرقاء فقط في المخطط الدائري في (C).
ويأتي مفهوم الوقت الفاصل بين الأحداث كأحد المفاهيم المفتاحية التي يجب أخذها في الاعتبار، وهو في هذه الحالة المدة بين حافلتين متعاقبتين. ويشير الجدول في الشكل 2A، إلى أنه في كل ساعة تصل 6 حافلات بعد وقت فاصل بين كل حافلة مدته 4 دقائق (باللون الأزرق)، وتصل ثلاث حافلات مباشرة بعد وقت فاصل بين كل حافلة مدته 12 دقيقة (باللون الأحمر). وفي هذا السيناريو، نفترض أنك وصلت إلى محطة الحافلات دون أن تعرف متى تصل الحافلة القادمة، وطبقًا لنظرية الاحتمال، فسنقول إنك تصل إلى محطة الحافلات في وقت عشوائي بصورة منتظمة، هل تعتقد أن احتمالية انتظارك لمدة 4 دقائق بين الحافلات أكثر رجحانًا، أم أن احتمالية انتظارك 12 دقيقة أكثر رجحانًا؟ إذا كانت المدة بين الحافلات 4 دقائق، فلن تضطر إلى الانتظار طويلًا حتى تصل الحافلة القادمة، أما إذا كانت المدة 12 دقيقة، فربما تحتاج إلى الانتظار لمدة طويلة. وكما ذكرنا أعلاه، فهناك 6 مرات تكون فيها المدة بين الحافلات 4 دقائق و4 مرات تكون 12 دقيقة.
فكِّر في الأمر بهذه الطريقة: ربما تكون احتمالية انتظارك لمدة 4 دقائق أكثر، لأنها تحدث 6 مرات في الساعة، ولكن مدة 12 دقيقة تحدث فقط 3 مرات في الساعة. فالأولى تحدث باحتمالية 6/(6 + 3) = 3/2 التي تعتبر حوالي 0.67، ما يعني أن الموقف يحدث بنسبة 67% (انظر الشكل 2B)، والأخيرة تحدث باحتمالية 3/(6 + 3) = 3/1، ما يعني أن الموقف يحدث بنسبة 33%، ولكن للأسف، هذه طريقة تفكير أشبه بالأحلام.
إن الوصول إلى محطة الحافلات في وقت عشوائي منتظم، يشبه لف عجلة دوارة تحتوي على شرائح عليها أرقام من 0 وحتى 59 (وبالتالي تكون بها 60 شريحة)، ثم إيقاف هذه العجلة بإصبعك، والنظر إلى الرقم المدون على الشريحة التي تضع إصبعك عليها. وإذا كان إصبعك يشير إلى الرقم 33، فهذا يعني أنك وصلت إلى محطة الحافلات في تمام الساعة 10:33. وفي هذه الحالة، عليك الانتظار لمدة 3 دقائق حتى تصل الحافلة القادمة التي تصل الساعة 10:36. وهذه العجلة تمنحنا الطريقة لفهم مدلول “العشوائية المنتظمة ”. ولونت كل دقيقة على العجلة باللون الأزرق، للدلالة على مدة الانتظار البالغة 4 دقائق بين الحافلات، وبالأحمر للدلالة على المدة البالغة 12 دقيقة. وفي الشكل 2C، نرى أن هناك 24 دقيقة زرقاء و36 دقيقة حمراء. ويتضح من خلال هذه الصورة، أن احتمالية وقوع وقت الانتظار الذي بلغ 12 دقيقة أكثر (فهذا يحدث بنسبة احتمال 0.60)، مقارنة بنسبة وقوع وقت الانتظار 4 دقائق (الذي تبلغ نسبة احتماليته 0.40) (انظر الشكل 2D).
وبالرغم من أن هناك 3 توقيتات تبلغ مدتها 12 دقيقة من أصل 9 توقيتات إجمالًا (أي أن نسبة حدوثها 1/3)، فإن احتمالية حدوثها تعتبر أعلى (تبلغ نسبة حدوثها 0.60) مقارنة بوقت الانتظار الذي يبلغ 4 دقائق. ما تفسير هذا الأمر؟ تأتي الإجابة من خلال حقيقة بسيطة: إن أوقات الانتظار الطويلة طويلة، والأوقات القصيرة قصيرة؛ أي أن وقت الانتظار الطويل يحتل 12 رقمًا في العجلة الدوارة، بينما يحتل الوقت القصير 4 أرقام فقط، وأوقات الانتظار الطويلة الثلاثة مجتمعة، تغطي نسبة 12×3 = 36 من الـ 60 دقيقة. وعلى العكس، فإن أوقات الانتظار القصيرة الستة تغطي فقط 4×6 = 24 دقيقة. ومن ثم، فإن قلة ورود مدة انتظار ما في جدول الحافلات، لا يعني أن مصادفة وقت الانتظار ذلك أمر نادر. إنما بإجراء بعض الحسابات على جدول الحافلات في الشكل 2A، سنجد أن التخمين الساذج لمدة الانتظار المتوقعة (نصف مدة الوقت الفاصل بين مرور الحافلتين) هو 3 دقائق و20 ثانية، ولكن وقت الانتظار الحقيقي هو 4 دقائق و24 ثانية. في الجدول في الشكل 1B، يكون التخمين الساذج لوقت الانتظار هو 3 دقائق أما الوقت الحقيقي للانتظار هو 3 دقائق و40 ثانية. ولنفترض أن جميع أوقات الانتظار مدتها 6 دقائق، مما يعني أن الحافلة تصل بالضبط كل 6 دقائق، في هذه الحالة لا يكون هناك مفارقة وقت الانتظار، لأن التخمين الساذج يتساوى مع وقت الانتظار الفعلي الذي يبلغ 3 دقائق، ولكي تحدث مفارقة وقت الانتظار، نحتاج إلى وجود فترتين مختلفتين على الأقل بين الأحداث، مثل أن يكون هناك 4 دقائق و12 دقيقة.
التطبيقات والامتدادات
تنطبق مفارقة وقت الانتظار على مواقف كثيرة، أكثر من مجرد انتظار الحافلات، فالأوقات بين الأحداث لها أهمية كبيرة في العديد من المواقف. فلنتخيل “حدث” التحدث إلى زميل في المدرسة. وتشير الأوقات بين الأحداث، إلى مقدار المدة بين المحادثات الجارية بين الزملاء (انظر الشكل 3A). قد يكون مقدار الوقت بين الأحداث دقيقتين، ومقدار الوقت التالي يكون 11 دقيقة، وفي الأنشطة الاجتماعية، بخلاف جداول الحافلات، عادةً ما يكون هناك تنوع كبير في الأوقات بين الأحداث. ففي الشكل 3B، نوضح مدرجًا تَكراريًا للأوقات الفاصلة بين الأحداث لطالب في مدرسة في فرنسا [3]. وقمنا بوضع التوقيتات من اليسار إلى اليمين بترتيب متصاعد في المدرج التَكراري، ويشير ارتفاع كل عمود في المدرج التكراري، إلى عدد مرات حدوث كل وقت من الأوقات بين الأحداث. ونلاحظ أن أغلب الأوقات بين الأحداث قصيرة (20 ثانية أو 40 ثانية)، ولكن عدد قليل من هذه الأوقات مدته طويلة (تتراوح ما بين 200 إلى 400 ثانية).
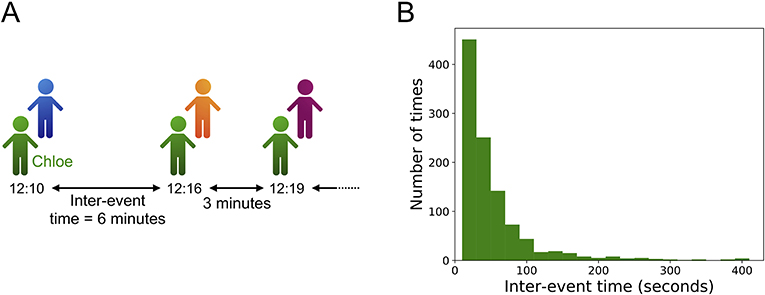
- شكل 3 - الأوقات بين الأحداث لطالب يقوم بأنشطة اجتماعية في المدرسة.
- (A) الأوقات بين الأحداث لطالبة تدعى Chloe. تتحدث Chloe مع ثلاثة طلاب مختلفين، بأوقات بين الأحداث تبلغ 6 دقائق و3 دقائق. (B) مدرج تَكراري للأوقات بين الأحداث لطالب في مدرسة في فرنسا. ويأتي هذا المثال من بيانات “Primary School” الواردة في مشروع SocioPatterns [3]. قمنا باختيار الطالبة التي لديها أعلى عدد من الأحداث، وقمنا بحساب جميع الأوقات بين الأحداث الخاصة بهذه الطالبة. وتشير الأعمدة في هذه الصورة، إلى عدد الأوقات بين الأحداث لكل مدة خاصة بهذه الطالبة، ويوضح المدرج التكراري أن هناك تنوعًا كبيرًا في الأوقات بين الأحداث، أغلب هذه الأوقات قصيرة، إلا أن بعضها طويل للغاية.
في المثال الذي أوردناه عن مفارقة وقت الانتظار الخاصة بالحافلات، رأينا أنه حتى وإن كانت هناك ثلاثة أوقات انتظار طويلة فقط من إجمالي 9 أوقات، فإن احتمالية حدوث مدة الانتظار الطويلة، أكثر من احتمالية حدوث مدة الانتظار القصيرة، ويعد هذا مثالًا على المعاينة المتحيزة. والمثال الآخر على المعاينة المتحيزة هو مفارقة الصداقة [4, 5]. فبالنسبة لمفارقة الصداقة، يميل أصدقاؤك لأن يكون لديهم أصدقاء مثلك، ولكن لا يوجد داع للغضب، لأنها أيضًا ظاهرة رياضية خالصة. فإذا كان لديك 20 صديقًا في المدرسة، فسيكون أكثرهم في الأغلب من الشخصيات الاجتماعية البارزة. على سبيل المثال، إذا كان لأحمد صديق واحد فقط، ففي الغالب هذا الصديق ليس أنت، بل شخص آخر، وعلى العكس، إذا كان إبراهيم صديقًا لنصف الطلاب في المدرسة، ففي الأغلب أنت واحد من هؤلاء الأصدقاء. وقد يبدو أن الانتظار للحافلة القادمة وحساب عدد الأصدقاء، ليس لهما علاقة ببعضهما بعضًا، إلا أن من المنظور الرياضي احتمالية أن يكون لديك صديق مثل إبراهيم، مبنية على نفس السبب الذي يجعلك من المحتمل أن تركب الحافلة بعد مدة انتظار طويلة. فتخيل مثلًا أن هناك 6 طلاب لكل منهم 4 أصدقاء، و3 طلاب لكل منهم 12 صديقًا. إذا كنت صديقًا لطالب واحد فقط من هؤلاء الـ9، ففي الأغلب سيكون صديقك ممن لديه 12 صديقًا، حتى وإن كان عددهم 3 طلاب فقط لديهم 12 صديقًا ضمن مجموع 6 + 3 = 9 طلاب. هذه هي الأرقام ذاتها التي استخدمناها في الشكل 2، لشرح مفارقة وقت الانتظار، وهذا يوضح أن كلًا من مفارقة وقت الانتظار ومفارقة الصداقة، لهما نفس الأسس الرياضية، وكلاهما ناتج عن المعاينة المتحيزة.
ويعتبر فهم مفارقة وقت الانتظار مهمًّا في الكثير من المواقف، مثل فهم مدى سرعة انتشار الأمراض في مجموعة ما [6]. وتظهر مفارقة وقت الانتظار عادةً في موضوعات المواد التعليمية الجامعية والبحث العلمي؛ مثل نظرية الاحتمال ونظرية الأرتال أو الطابور وتحليل الشبكات.
كما رأينا أن الرياضيات تقدم لنا طريقة لتوحيد الأفكار التي تبدو مختلفة، لنرى كم هي مترابطة، وهذه القاعدة حقيقية، ليس فقط في مفارقة وقت الانتظار ومفارقة الصداقة، بل في العديد من الأشياء الأخرى التي نصادفها في حياتنا اليومية.
مسرد للمصطلحات
مفارقة وقت الانتظار (Waiting-Time Paradox): ↑ هي ظاهرة قائمة على علم الرياضيات خاصة بأوقات الانتظار، وقد تبدو غير منطقية، إلا أنها في الواقع صحيحة. ففي مفارقة وقت الانتظار، إذا حدث أمر ما نقوم به عشوائيًا بصورة منتظمة، فسيكون وقت الانتظار حتى الحدث القادم أكبر عادة من نصف مدة الانتظار بين الحدثين، ويطلق على مفارقة وقت الانتظار “مفارقة الحافلات” و“مفارقة التفتيش” أيضًا.
الوقت الفاصل بين الأحداث (Inter-Event Time): ↑ هو الوقت الفاصل بين حدثين متعاقبين، مثل وصول حافلتين في محطة الحافلات، أو أن يقوم شخص بإجراء محادثتين مع أشخاص آخرين.
نظرية الاحتمال (Probability Theory): ↑ وهي مادة في الرياضيات تتمحور حول موضوعات تتعلق بالـ “الاحتمالات”، التي تعتبر وصفًا رقميًّا لمدى أرجحية حدوث نتيجة أو حدث ما، و“توزيع الاحتمالات”؛ هي العملية الرياضية التي تعطي الاحتمالات لحدوث كل النتائج الممكنة، لشيء أو حدث ما.
العشوائية المنتظمة (Uniformly at Random): ↑ توزيع الاحتمالات الذي تكون فيها فرصة حدوث كل الاحتمالات متساوية.
المدرج التكراري (Histogram): ↑ وهو المخطط الذي يوضح عدد العناصر في مختلف النطاقات من الأرقام، بهدف مقارنة عدد العناصر في كل نطاق. على سبيل المثال؛ المدرج التكراري الذي يوضح الأطفال في مراحل عمرية ما بين 0-4 سنوات و5-9 سنوات و10-14 سنوات، وهكذا. وارتفاع عمود الأطفال الذين تتراوح أعمارهم بين 10-14 سنوات، يشير إلى عدد الأفراد الذين تتراوح أعمارهم بين 10 و14 سنة.
المعاينة المتحيزة (Biased Sampling): ↑ تحدث المعاينة المتحيزة عندما يقوم شخص باختيار عناصر (أو لدقة التعبير يأخذ عينات)، مثل الأوقات بين الأحداث الطويلة أو الشخص الذي لديه الكثير من الأصدقاء، من مجموعة من العناصر المتكررة بمعدل أكبر من غيرها من العناصر، نتيجة للقواعد التي يبني عليها عملية الاختيار.
إقرار تضارب المصالح
يعلن المؤلفون أن البحث قد أُجري في غياب أي علاقات تجارية أو مالية يمكن تفسيرها على أنها تضارب محتمل في المصالح.
شكر وتقدير
نحن ممتنون لقرَّائنا الشباب - Nia Chiou وTaryn Chiou وValerie E. Eng وAnthony Jin وIris Leung وMaple Leung وAmi Masuda وRitvik Mukherjee لتعليقاتهم المرشدة والمفيدة. كما نشكر والديهم ومعلميهم وأصدقاءهم - Lyndie Chiou وChristina Chow - لجعلنا على اتصال معهم والتماس آرائهم. ونشكر Iris Leung لرسم الشكل 1A. ونشكر حكامنا ومحررينا لاقتراحاتهم المرشدة وممتنون لتعاون SocioPatterns (انظر http://www.sociopatterns.org/) وتقديمها المعلومات اللازمة. وتقدر NM الدعم من AFOSR European Ofice (رقم المنحة 9550-19-1-70FA). كما تقدَّر MAP الدعم من the National Science Foundation (رقم المنحة 1922952) من خلال برنامج (Algorithms for Threat Detection (ATD).
المراجع
[1] ↑ Welding, P. I. 1957. The instability of a close-interval service. J. Oper. Res. Soc. 8:133–42. doi: 10.1057/jors.1957.21
[2] ↑ Masuda, N., and Hiraoka, T. 2020. Waiting-time paradox in 1922. Northeast J. Complex Syst. 2:1. doi: 10.22191/nejcs/vol2/iss1/1
[3] ↑ Isella, L., Romano, M., Barrat, A., Cattuto, C., Colizza, V., Van den Broeck, W., et al. 2011. Close encounters in a pediatric ward: Measuring face-to-face proximity and mixing patterns with wearable sensors. PLoS ONE 6:e17144. doi: 10.1371/journal.pone.0017144
[4] ↑ Feld, S. L. 1991. Why your friends have more friends than you do. Am. J. Sociol. 96:1464–77. doi: 10.1086/229693
[5] ↑ Strogatz, S. 2012. Friends You Can Count On. The New York Times. Available online at: https://opinionator.blogs.nytimes.com/2012/09/17/friends-you-can-count-oni
[6] ↑ Karsai, M., Kivelä, M., Pan, R. K., Kaski, K., Kertész, J., Barabási, A. L. et al. 2011. Small but slow world: how network topology and burstiness slow down spreading. Phys. Rev. E 83:025102(R). doi: 10.1103/PhysRevE.83.025102
