摘要
我们的世界充满着谜题, 从身边司空见惯的现象, 比如风吹树枝, 到只有在特定条件下才会发生的罕见且神秘的现象, 比如超流体, 即极低温度下一些液体可以永无止尽地流动, 而物理学是破解自然界谜题的最佳工具之一。超流体就是我在我的物理学之旅中遇到的一种非常特殊的现象。平凡无奇的液体, 当温度降低到某一温度之下后, 基本性质会突然改变, 没有了黏性, 可以一直流动, 甚至向上爬出容器口, 即变成了超流体。在这篇文章中, 我将带你走近超流体的迷人世界, 展示它们的一些有趣的行为, 并解释其与使我获得 2016 年诺贝尔物理学奖的发现有何联系。
迈克尔 ⋅ 科斯特利茨 (Michael Kosterlitz) 教授, 因在物质的拓扑相变和拓扑相领域的理论性发现, 与戴维 ⋅ 索利斯 (David James Thouless) 教授和邓肯 ⋅ 霍尔丹 (Frederick Duncan Michael Haldane) 教授共同获得 2016 年的诺贝尔物理学奖。
拓扑学: 形状的数学语言
拓扑学是数学的一个分支领域, 研究物体的形状, 并根据形状将物体分类。关于形状的一个关键参数是洞的数目。例如, 球没有洞, 而甜甜圈有一个洞 (图 1A)。因此, 球和甜甜圈在拓扑学上属于不同类别, 意思是, 你把球平滑地变形, 不可能变成甜甜圈, 要把球变成甜甜圈, 必须在球上戳一个洞, 这就需要撕裂材料, 就不叫平滑地变形了。在拓扑学中, 你可以随心所欲地揉捏材料, 但你不能戳洞, 也不能把不同部分粘在一起。因此, 你可以把一个球揉成一个碗, 因为它们的拓扑结构是相同的。这波操作很滑稽, 背后的思想颇有用。
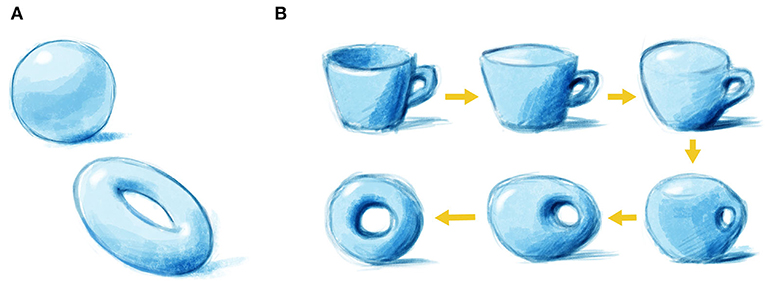
- 图 1 - 拓扑和形状。
- (A) 球没有洞, 而甜甜圈有一个洞——因此, 它们在拓扑学上属于不同类别。(B) 甜甜圈和咖啡杯都有一个洞, 因此在拓扑上是等价的。这意味着我们可以以一种平滑的方式, 不撕裂材料也不将洞粘上——拓扑变形中禁止这两种情况, 从一种形状转变成另一种形状。发生在物理学中的类似现象, 就可以考虑拓扑的思想, 而且很有用。
拓扑学上如何看待甜甜圈和带把手的咖啡杯?它们乍看起来大不一样, 但如果你仔细观察, 就会发现, 它们都有一个洞。从拓扑学的角度来看, 这意味着甜甜圈和咖啡杯是等价的。用专业术语来说, 它们具有拓扑等价性。因此, 您可以以平滑和连续的方式将它们相互转换 (图 1B)。因此, 在这种情况下, 洞的数目可称为拓扑不变量——在物体变形过程中保持不变的量, 或者说相对于甜甜圈和咖啡杯保持不变, 即使这些物体经历了改变外观的操作。
拓扑学语言还可用于描述某些材料的性质, 这样的材料因此称为拓扑材料。在下一节中, 我们将简要介绍拓扑学如何帮助我们识别材料之间的差异, 以及如何帮助我们解释某些不同寻常的和令人兴奋的现象, 比如貌似不受重力影响的流体。
拓扑材料: 从平凡到怪异
如前文所述, 拓扑学是描述材料之间某些差异的一种方便方法。我们都很熟悉的一类材料叫做绝缘体。绝缘体是一种不易导电的材料, 如橡胶或塑料。材料导电还是不导电由材料的能量特性决定。材料中的电子的能量不是任意值都可以的, 这些离散的特定能量称为能级, 材料中许许多多的能级密集排列在一起, 构成能带。材料很多性质通常取决于能带结构。电子依次充满能量较低的能带, 而将高能量的能带空着, 空能带与被占能带之间的能量差叫做“能隙”, 对于绝缘体来说, 能隙非常大, 电子没有足够的能量跑到空置的高能带。对于导体来说, 空能带与被占能带是连在一起的, 没有能隙, 电子不需要额外能量就能跑到空能带上, 还能“跑来跑去”, 材料加上电压, 电子就一起从电压低的地方向电压高的地方跑, 形成电流(点击这里, 了解更多关于绝缘体、导体能带的信息)。绝缘体系统的能带结构可以根据拓扑不变量进行分类, 拓扑不变量即在系统状态改变时也能保持不变的性质。这意味着我们可以根据绝缘体电子一定能量下对应的微观状态的拓扑性质来给绝缘体命名和分类。
在过去 15 年左右的时间里, 有一类特殊的绝缘体——可以使用拓扑不变量进行分类和描述, 因此称为拓扑绝缘体——引起了人们的极大兴趣。这种材料内部绝缘, 表面导电。[1] 拓扑绝缘体同时具有导电和绝缘的性质, 是怎么做到的呢?在这些材料的中间部分, 即所谓的本体, 电子做圆周运动, 圆周半径很小, 且离得很近, 电子不能四处移动 (图 2C)。因此, 拓扑材料本体部分是绝缘的, 就像塑料或橡胶一样 (图 2A)。但是, 在拓扑材料的表面, 电子的运动状态很特殊, 可以沿边缘移动 (图 2C)。这意味着拓扑绝缘体的表面是导电的, 就像金属一样 (图 2B)。你可能会想, “好吧, 这很酷, 有什么用吗?” 直到今天, 这个问题还在困扰着许多物理学家和计算机工程师。让我们一窥可能的答案。
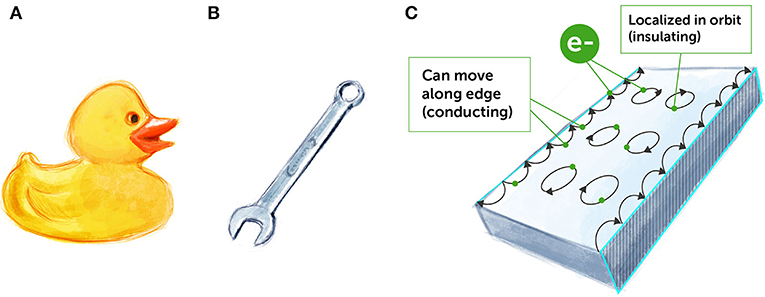
- 图 2 - 绝缘体和导体。
- (A) 橡胶是绝缘体, 不容易导电。(B) 金属是导体, 容易导电。(C) 拓扑绝缘体具有特别的导电性质, 在内部, 电子做圆周运动 (“局域化的”), 行为类似绝缘体, 在表面, 电子可以自由移动, 表现得像导体 (沿边缘 “巡游”)。
拓扑绝缘体有什么用?
拓扑绝缘体表面的导体状态非常稳定, 经得住材料的缺陷和扰动。之所以具有韧性适应力和稳定性(可总称为健壮性, 或鲁棒性), 一个主要原因是, 其特性往往依赖于整个系统, 而不仅仅是系统的一小部分或特定位置的几个原子。你可以把它看作是材料整体的集体现象。这意味着即使存在一些小的东西, 比如材料中的局部缺陷, 它仍然不会对整个系统产生显著影响, 因此不会改变系统的拓扑态 [2]。
这有什么用呢? 拓扑绝缘体的健壮性使其可用于制造更好的计算机, 因为它性能稳定, 而稳定是计算元件 (即计算机中执行计算的元件) 最基本的要求, 因为我们希望这些元件每次运行能给出一样的结果, 并且尽可能少出错。因此, 拓扑绝缘体未来在改进计算元件方面具有巨大的潜力。然而, 实现这一具体技术应用的过程, 存在重大的技术挑战, 所以计算机真的用上拓扑绝缘体, 我们还有很长的路要走, 但在未来可能会实现。
现在, 我将带你进一步深入拓扑材料的迷人世界, 并向你展示我对物理学中最奇特的现象之一——超流的解释。
会飞的流体: 冷氦的故事
你知道吗?有些液体可以克服重力, 爬上玻璃器壁。这是我们在日常生活中不会遇到的怪异的物理现象, 引起了科学家的极大兴趣。这样的流体被称为超流体, 这是流体在极低的温度下表现出的非常奇怪的行为。最常见的超流体是液氦, 4He。氦在常温常压下是气体, 很多会飞的气球里就是充的氦气。人吸入氦气, 嗓音会变得奇怪, 像唐老鸭。温度非常低时, 气体氦会变成液体氦。温度继续降低到接近 −270.98∘C 或绝对零度时, 它会从一般流体转变为超流体(这个温度叫作 λ 点, 在1个标准大气压下约为 2.17 K)。
1972 年, 三位物理学家发表了一项绝妙的实验 [3]。他们将一个石英晶体置于氦气中, 通过调节气体的压强, 改变吸附在石英晶体表面的氦的总量, 从而形成了一层氦薄膜, 只有两到三个原子厚。石英晶体的固有振动频率与振动晶体的总质量有关, 质量越大, 振动频率越小。当一层薄薄的氦原子粘在晶体表面时, 一个自然的想法是, 这些原子会随着晶体表面一起运动, 它们唯一的效应就是增加振动物体的质量, 将略微降低其固有振动频率。用一个振动带动一个物体振动, 当外界的振动的频率与物体固有频率相等时, 振动最强烈, 这叫共振。物理学家对吸附有氦薄膜的石英晶体做共振实验, 发现当气压比较低、氦吸附量比较小时, 共振频率随吸附量的增大而减小, 与预期一样。然而, 随着气压和氦吸附量的增加, 共振频率开始偏离预期, 不再下降, 而是升高 (图 3A), 好像氦薄膜不再随着晶体运动了。
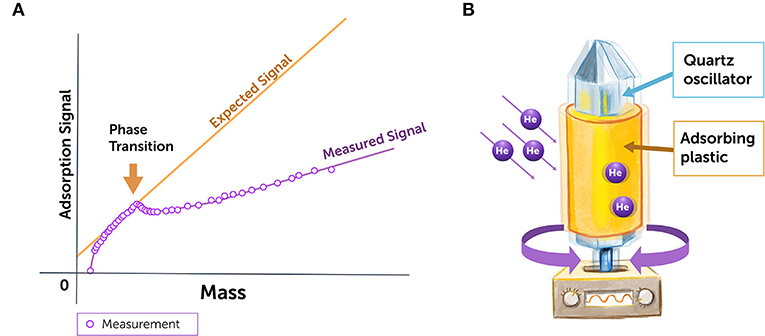
- 图 3 - 超流氦实验。
- (A) 低温下, 石英晶体吸附数层氦薄膜后, 实测振动频率偏离预期值。纵坐标吸附信号为振动频率的变化量, 即无氦薄膜时的频率减去有氦薄膜时的频率, 横坐标质量表示吸附在晶体表面的氦的量。石英晶体吸附上正常态的氦, 质量增加, 振动频率降低。但如果部分氦变成超流体, 这部分氦不会增加石英晶体的质量, 因此振动频率的减小量比正常氦要小(改编自 Chester et al. [3])。(B) 实验的改进版 [4], 可以进行频率更低的振动, 将一层聚酯塑料薄膜包在扭转振动的石英棒上, He-4 气体吸附在塑料薄膜上, 测量共振频率和耗散。这个实验与前一个实验的原理相同, 但测量结果更准确和细致。
几年后, 这个实验有了更复杂的版本。棒状石英晶体外面又包了一圈塑料膜, (图 3B), 然后使其振动起来, 物理学家测量其频率。增大振 动棒周围氦气的压强, 再次测量了石英棒的振动频率。当氦原子与有吸附性的塑料表面相遇时, 通常会吸附 (锁定) 在塑料上, 在棒周围形成一层薄膜, 并增加其质量。结果, 振动系统的固有频率有轻微的降低, 与预期一致, 因为质量越大, 振动频率越低。
这个实验结果最简单的解释是, 部分氦薄膜变成超流体后, 它就不再粘在振动物体上了。正常氦和超流氦之间的区别在于它们的流动方式。正常氦会附着在它流过的任何东西上, 这是由于一种叫做耗散的特性造成的。然而, 超流氦自由流动, 没有耗散, 与其说是流动, 不如说是在 “飞行”, 只是飞得太低, 盘旋在它所流经的物体之上 (点击这里和这里可以观看有趣的超流氦展示)。
这是一个开创性的实验, 表明氦薄膜在低温下会变成超流体。问题是, 当时还没有理论可以解释薄膜氦中这种行为的变化, 即从正常液体到超流液体的转变, 这是一种相变, 相变即系统的两种状态之间的突然切换, 系统的性质随之发生变化。例如, 液态水转变为固态冰。当时的一个普适理论甚至预测, 在那样的实验条件下, 这样的相变不应该发生, 二维薄膜中不可能变成超流体。事实上, 这个实验与一个广被接受的原则相悖, 这个原则与任何系统的低温相的本质相关。有一个严格的数学定理表明, 二维系统的低温相在任何温度下都不可能长程有序, 即原子或分子不能在很远的距离内都有规律地排列, 这意味着在二维氦薄膜中不可能出现超流态。现在, 实验和严格的理论有严重冲突, 理论暗示薄膜中不可以出现超流态, 而实验观察却恰恰相反。显然, 实验和理论, 二者必有其一是错误的或被错误解释的, 因为实验清楚地表明, He-4 薄膜可以发生相变, 变成超流体。这就是我当时的导师戴维 • 索利斯教授和我进入这个领域的原因: 我们要提出一种新理论, 解释氦薄膜在超流体和正常流体之间的相变, 解决实验和理论之间的矛盾。
涡旋: 超流氦的 “幕后”
正如我前文所说, 液氦有两个相, 正常相和超流相。正常流体在流动时会伴随耗散, 这意味着它会与所流经的表面相互作用, 与之交换能量, 并粘在上面。处于超流相的液氦自由流动, 没有耗散, 好像盘旋于它流经的表面上一样。为了理解正常氦和超流氦之间的相变, 我们必须弄清楚耗散的机制。
后来发现, 答案在一种特殊的结构——涡旋 (图 4)。由于量子力学上的原因, 超流体中可以激发出一种涡旋, 它是唯一能够平息流动的超流体的激发, 这也能解释, 为什么石英振动棒包不包聚酯塑料薄膜, 实验现象和理论解释都是一样的。聚酯塑料薄膜的唯一作用是它与涡旋之间的摩擦, 但它对超流体没有影响。为了简单起见, 你可以把涡旋想象成打转的流体, 就像浴缸的塞子拔出来时流入下水口的水一样。要理解这些事情, 你必须学习很多物理知识, 现在你只需要记住, 这些超流体中的涡旋是唯一需要考虑的激发。在二维空间中, 低温下, 顺时针转动的涡旋与逆时针转的涡旋结成对, 当温度比较高时, 成对的涡旋解体, 变成两个自由的涡旋, 扩散到流体的边缘。这些涡旋以中性对形式形成, 在极低温度下, 一个涡旋逆时针旋转, 另一个涡旋顺时针旋转, 但在较高温度下, 这些涡旋解绑定为两个自由涡旋, 漂移到流体边缘, 在那里消失不见, 从而略微降低了超流体流动的均匀性 (图 4B)。这是在正常体流动中进行能量耗散的方式。由于液氦流动的两种状态可以定义为两种拓扑态, 液氦也被认为是一种拓扑材料——很像我们之前讨论过的拓扑绝缘体(点击这里了解更多关于拓扑材料和涡旋的信息)。
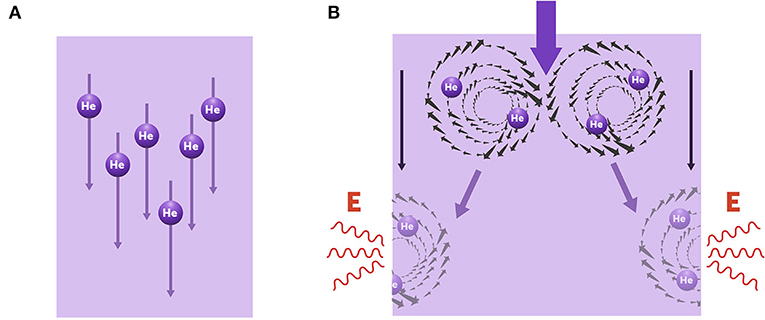
- 图 4 - 液氦中的相变机制。
- (A) 在超流氦中没有涡旋, 所以流体自由流动, 没有耗散。(B) 在正常氦中, 成对的漩涡出现 (上) 并漂移到流体相对的两个边缘, 在那里它们消失并释放能量 (下)。这一过程产生了耗散, 并减慢流速, 导致更多耗散。
发现超流体系统的基本物理涉及涡旋的相互作用后, 我们建立了一个数学模型来解释液氦的相变, 以及类似系统中的其他相变, 准确度非常高 [4 – 7]。这是一个重要的进展, 使我们在理解拓扑材料的一些惊人特性方面向前迈出了一大步。最后, 我想就我对数学和物理的热爱, 以及如何生活得幸福, 给年轻的读者们谈一点个人的看法。
给小读者的建议
可爱的符号: 数学和物理之美
我上学刚学代数时, 我想: “哇, 这是一种很棒的做事方式——比算术强得多!” 因为代数能让我解决以前不容易解决的数学问题。这就像打开了一盏明灯, 突然使各种各样的事情成为可能!我立刻爱上了符号, 因为数学符号消除了很多混乱, 让事情变得简单。我知道并不是每个人都有这样的看法, 因为这取决于每个人的思考方式。但对我来说, 处理符号和方程是有趣的和令人兴奋的, 直到今天我都很喜欢它。在某种程度上, 对我来说, 做物理就像攀岩——我的另一个爱好, 置身于未知的地方, 完全靠自己, 自己对自己的行为负责, 努力找到前进的方向 (图 5)。物理的优点是, 犯错的惩罚比攀岩轻!

- 图 5 - 给青少年的一些建议。
- 使用符号和方程类似于攀岩。你出发探索未知的世界, 自己对自己的行为完全负责, 同时努力找到自己的方向。我觉得这很令人兴奋。
如何选择你的职业
你应该做你喜欢和擅长的事情。无论做什么, 都要做成你擅长的事情, 这很重要, 如果你擅长它, 你可能就会喜欢做它。我还认为, 你应该从你所做的事情中获得乐趣, 因为如果你不能从中获得乐趣并享受你的工作, 那么它就不值得做。所以, 这是我可以给年轻读者的一条建议——过得快乐, 因为你只有一次生命, 不快乐的生活不值得过。
术语表
拓扑学 (Topology): ↑ 数学的一个分支领域, 研究如何描述物体形状变化。
拓扑材料 (Topological materials): ↑ 性质可以用拓扑学描述的材料。
拓扑绝缘体 (Topological insulators): ↑ 一种材料, 同时是绝缘体和导体, 内部绝缘, 表面导电。
超流体 (Superfluids): ↑ 流动无耗散 (即不存在黏滞现象) 的流体。
振动频率 (Oscillation frequency): ↑ 振动物体——称为振子——单位时间内完成一次完全振动的次数。
耗散 (Dissipation): ↑ 系统损失的能量 (比如摩擦产生的热), 这部分能量要回收过来, 单能靠系统自己复原是做不到的, 要额外注入能量才可以。
相变 (Phase transition): ↑ 系统在两种状态之间的突变, 系统性质随之而变, 比如液态水变成固态冰就是一种相变。
利益冲突声明
作者声明, 该研究是在没有任何可能被解释为潜在利益冲突的商业或财务关系的情况下进行的。
致谢
感谢 Noa Segev 的采访为本文奠定了基础, 她也是论文的合著者。感谢 Alex Bernstein 提供图表, 感谢 Susan Debad 对稿件的修改。同时还要感谢 Subramanian Ramachandran 博士对稿件提出的宝贵意见。感谢赛先生公众号及译者瞿立建、陈晓雪对本文中文翻译的贡献。
参考文献
[1] ↑ Moore, J. E. 2010. The birth of topological insulators. Nature. 464:194–8. doi: 10.1038/nature08916
[2] ↑ Qi, X. L., and Zhang, S. C. 2010. The quantum spin hall effect and topological insulators. arXiv preprint. arXiv:1001.1602. doi: 10.1063/1.3293411
[3] ↑ Chester, M., Yang, L. C., and Stephens, J. B. 1972. Quartz microbalance studies of an adsorbed helium film. Phys. Rev. Lett. 29:211. doi: 10.1103/PhysRevLett.29.211
[4] ↑ Bishop, D. J., and Reppy, J. D. 1978. Study of superfluid transition in 2-dimensional 4He films. Phys. Rev. Lett. 40:1727. doi: 10.1103/PhysRevLett.40.1727
[5] ↑ Kosterlitz, J. M., and Thouless, D. J. 1973. Ordering, metastability and phase transitions in two-dimensional systems. J. Phys. C Solid State Phys. 6:1181. doi: 10.1088/0022-3719/6/7/010
[6] ↑ Kosterlitz, J. M. 2016. Kosterlitz–Thouless physics: a review of key issues. Rep. Prog. Phys. 79:026001. doi: 10.1088/0034-4885/79/2/026001
[7] ↑ Hadzibabic, Z., Krüger, P., Cheneau, M., Battelier, B., and Dalibard, J. 2006. Berezinskii–Kosterlitz–Thouless crossover in a trapped atomic gas. Nature. 441:1118–21. doi: 10.1038/nature04851
