Abstract
Gravity is a universally attractive force, which tries to cause matter to clump. This means that in diverse physical systems, ranging from stars at the end of their lives burning nuclear fuel, to gas clouds which collapse under the weight of their own gravity, a natural endpoint can be the development of a black hole. This is an object where matter has been packed so densely that even light cannot escape gravity’s pull at its surface, or event horizon. Black holes are both commonplace—our own Milky Way galaxy hosts a giant black hole in its center!—and mysterious. In this article we discuss current thoughts about one of the mysteries of black holes—how one can explain the number of distinct (but similar) physical states they hide behind their event horizon. Physicists call this the black hole entropy.
1. What is Entropy?
The entropy in a physical system is a measure of the amount of messiness or arbitrariness characterizing the system. Systems in very special states—almost any hunk of normal matter at very low temperatures, or a very clean bedroom, for instance—have low entropy. In both cases this is because the constituents of the system have no choice about where to be. At low temperature, in a chunk of material, every atom sits at a place that minimizes the energy of the system. In a very clean room, every piece of clothing is folded and stacked in a drawer. In contrast, matter at high temperature, or a messy room, has high entropy. The atoms can be flying about every which way in hot matter. In a messy bedroom, shirts and shorts can be flung about the room willy nilly. The entropy of a system is defined as the logarithm of the number of possible configurations of its constituents (atoms for matter; shirts and shorts for the messy room) that would look roughly the same, to a casual observer.
For conventional objects like tables, rooms, or slabs of lead, it is no surprise that one can associate an entropy to the system. We know what these systems are made of, and how to count configurations of the underlying parts. To the great surprise of theoretical physicists, it was discovered in the early 1970s that to this list of commonplace system with an entropy, you can add black holes.
2. Black Holes and Bekenstein’s Insight
What is a black hole? Imagine taking a lump of matter at some fixed mass M, and crushing it. Einstein’s theory of gravity says that when you squeeze it into a small enough region of space—with a size known as the Schwarzschild radius, RS(M)—the object becomes a qualitatively new kind of beast, a black hole. A black hole is a clump of matter so dense that even light cannot escape its surface, or event horizon. Therefore, its interior workings remain a mystery to the outside world, including us! If you want to know in more detail what a “small enough region” means, we can say
where G is the gravitational constant and c is the speed of light. It is okay if you do not follow the details of the equation; the basic point is that if you put an amount of mass M or larger in a sphere of radius smaller than RS(M), then voila—it will become a black hole.
We are talking about really dense matter. For instance, to compress the Earth to the size required to make a black hole, you would have to reduce its radius from today’s 4,000 miles to ~9 mm! Happily, Nature has provided us with real life examples of black holes, so we do not need to do the work of making one. In fact, now you can even see a black hole—or more precisely, its surrounding neighborhood. A spectacular image of the black hole sitting in the galaxy M87—a huge black hole weighing almost 7 billion times as much as our sun—was recently produced by the Event Horizon Telescope collaboration [1]!
As a graduate student at Princeton in the 1970s, Jacob Bekenstein pondered the following puzzling question. An observer outside of a black hole can only see the event horizon—the interior is hidden. The physical properties of the event horizon are totally characterized by just a few numbers: in the simplest case, the mass M of the black hole.
But, thought Bekenstein, could not I have formed the black hole of mass M in many different ways? I could have formed it by throwing in many elephants, or alternatively, many wombats. What happened to the information about how the black hole was formed? The black hole must have an entropy!
Work of Bekenstein—and later more precise work of Bardeen, Carter, and Hawking—succeeded in proving beyond reasonable doubt that black holes do indeed have an entropy. And they were able to produce a formula for the entropy of a black hole as a function of its mass S(M) [2]. But the precise nature of the physical states that could account for S(M) remained mysterious.
3. Counting With Hardy and Ramanujan
Let us briefly change the subject, to another pair of heroes. One of the most dramatic stories in the mathematics of the 20th century is that of Hardy and Ramanujan [3]. Ramanujan, self-educated in higher mathematics and working a day job as a clerk in the Port of Madras while doing mathematical research at night, sent letters describing his results to a few well-known mathematicians. His letters were finally answered by the prominent Cambridge University number theorist G.H. Hardy, who said of the formulae Ramanujan included in the letters:
A single look at them is enough to show that they could only be written by a mathematician of the highest class. They must be true because, if they were not true, no one would have the imagination to invent them.
On the strength of these formulae, Hardy brought Ramanujan to Cambridge, where they engaged in one of the most famous collaborations in the history of mathematics.
One of their central results is easily explained: suppose you have 5 oranges, and you wish to divide them up among various friends. How many ways could you imagine dividing them up? Well:
So we see that there are 7 ways of dividing up 5 oranges: into one group of 5, two groups of 4 and 1, and so forth. We say that the number of partitions of 5 is 7. If we write a function that associates to each whole number the number of partitions p(n), then we can re-write this as
For small numbers (n), like 3, 4, or 5, computing p(n) is easy. But how about p(100)? If you start trying to figure this out, you will see that the partition numbers quickly grow out of hand! How are we to determine them?
Hardy and Ramanujan succeeded in doing this by developing an ingenious trick called “the circle method.” They came up with a formula that allowed them to roughly determine p(n) and, using this formula, a graph like that in Figure 1 could be created. On the x-axis we have n, while on the y-axis we have the accuracy of their estimate for p(n). (Partitions only make sense for whole numbers n, but their formula spits out an answer—and can be plotted—for all values of n.)
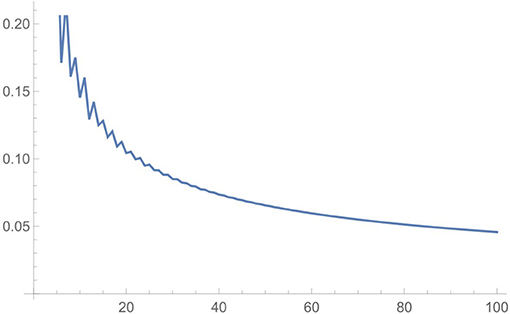
- Figure 1 - A plot of the accuracy of the Hardy-Ramanujan estimate for p(n) vs. n, for values of n up to 100.
- The label on the y-axis shows the fractional error of the estimate (so the y-value of 0.05 close to x = 100 means that the formula gets p(100) to within about 5% accuracy). Image credit to John D. Cook.
4. What About Black Holes?
We started with black holes, and then detoured into the partitions of positive integers. How are these two problems related?
To put these two subjects together, we first have to talk about a third subject, called string theory. String theory is one of the theories scientists use to describe the smallest things—even smaller than atoms—that make up the universe. In string theory, these fundamental objects are (tiny) loops of string. The lowest energy state of a tiny loop of string would be perfect stillness. You can also add energy to the string to create waves that can travel with various frequency around the loop. For instance, from Figure 2 (where we use a guitar string instead of a closed loop of string for ease of illustration), we see that the lowest frequency wave you can put on the string has one peak, while higher frequencies (often called higher harmonics in music!) have two, three, or more peaks. This allows multiple possible different waves on the string, with frequencies given by positive integers.
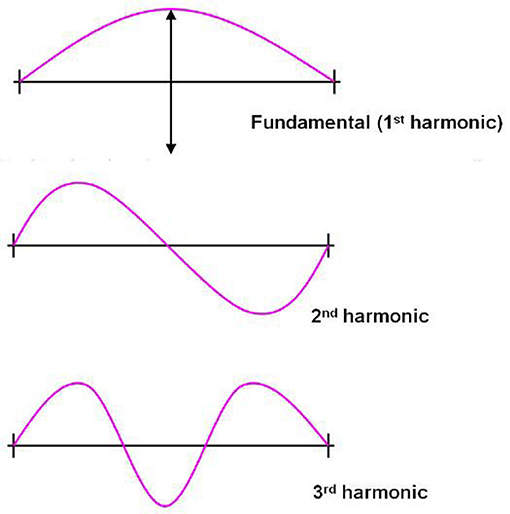
- Figure 2 - A guitar string has a lowest frequency of vibration, as well as higher harmonics which are integer multiples of this lowest frequency.
- Image credit to cronodon.com.
Importantly, we can also excite the string with two waves of the lowest frequency, or three, or more. Here, we are using the fact that energies present in the waves of a given frequency on the string are subject to quantum mechanics. A classical guitar string allows one to pluck the lowest frequency with any amplitude (and hence put any amount of energy into the string at that frequency). But quantum mechanics quantizes the energy present at a given frequency into discrete lumps—so one has a whole number (like 1.2, or 1,729, but not 2.718) times the energy associated to a wave at a given frequency.
Now, we are just a few steps away from figuring out how to compute black hole entropy in string theory! We rely on the following observations:
1. We could imagine waves with many different frequencies being simultaneously present on the string. Remember that all frequencies are positive integers, and we want to keep track of the number of “quantum lumps” present at each frequency.
2. The energy cost of these quantum lumps increases with k. Higher frequencies use more energy, with the kth frequency using k times as much energy as the lowest frequency.
3. Einstein’s most famous equation tells us that
That is, the energy of the vibrating string shows up as mass.
We conclude that we can compute the number of massive string states at an energy N times that of the lowest energy mode, in the following way, using the method of Hardy-Ramanujan described earlier. We can reach energy level N by having any number of excitations of the lowest frequency n(1), any number n(2) in the second lowest frequency, any number n(3) with the third frequency, and so forth. However, to attain total energy N we must have
But each choice of the set of numbers [n(1), n(2), etc.] appearing on the right-hand side of this formula is precisely exhibiting a partition of N! The number of massive string states at string mass level N, is given by the number of partitions of N into positive integers, p(N).
This is related to black holes because a highly excited, wiggling string in string theory, can theoretically be made to lie within its Schwarzschild radius and form a black hole. Since we know the mass of the string states as a function of N, and we know the number of such string states from p(N), we can produce a formula for the entropy S(M). This gives a (correct) prediction for the entropy of suitable black holes in terms of partition numbers [4]!
Glossary
Entropy: ↑ The amount of messiness or arbitrariness that goes into specifying a given physical system (or roughly, the number of ways it could be made).
Event Horizon: ↑ The surface of a black hole. If you are at the event horizon—or closer to the center—you cannot possibly escape being sucked in, even if you are a light ray, the fastest moving object known to modern physics!
Frequency: ↑ For a wave (e.g., of water, or displacement of a string), this is the number of times the wave reaches its maximum height per unit time.
Amplitude: ↑ Amplitude is a measure of the height of peaks of, e.g., waves of water or waves of displacement of strings.
Conflict of Interest
The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
This work was supported in part by the National Science Foundation under grant PHY-1720397.
References
[1] ↑ Event Horizon Telescope. Available online at: https://eventhorizontelescope.org (accessed April 24, 2020).
[2] ↑ Hawking, S. 1998. A Brief History of Time. New York, NY: Bantam.
[3] ↑ Kanigel, R. 2016. The Man Who Knew Infinity. New York, NY: Washington Square Press.
[4] ↑ Susskind, L. 2009. The Black Hole War. New York, NY: Back Bay Books.
