תַקצִיר
גרביטציה היא כוח משיכה אוניברסלי, שמנסה לגרום לחומר להתאסף. משמעות הדבר היא שבמערכות פיזיקליות מגוונות, החל מכוכבים בסוף חייהם כשהם שורפים דלק גרעיני, ועד לענני גז שקורסים תחת המשקל של הגרביטציה העצמית שלהם, נקודת סיום טבעית יכולה להיות התפתחות של חור שחור. זהו אובייקט שבו חומר ארוז בצפיפות כל כך גדולה, שאפילו אור לא יכול לברוח ממשיכתה של הגרביטציה בפני השטח שלו, הנקראים אופק האירועים. חורים שחורים הם בו בזמן מסתוריים ושכיחים – שביל החלב שלנו מארח חור שחור ענקי במרכזו!במאמר זה, נדון בתאוריות העכשוויות לגבי אחת מהתעלומות של חורים שחורים: כיצד אפשר להסביר את הכמות של מצבים פיזיקליים מובחנים (אולם דומים) שהם מחביאים מאחורי אופק האירועים שלהם. פיזיקאים מכנים זאת האנתרופיה של חור שחור.
1. מהי אנתרופיה?
האנתרופיה במערכת פיזיקלית היא מדד לכמות הבלגן או האקראיוּת שמאפיינת את המערכת. למערכות שנמצאות במצבים מיוחדים מאוד – כמעט כל מערך של חומר נורמלי בטמפרטורות נמוכות מאוד, או אפילו חדר שינה נקי מאוד, למשל – יש אנתרופיה נמוכה. בשני המקרים הסיבה לכך היא שלרכיבי המערכת אין ברירה אלא להיות איפה שהם. בטמפרטורה נמוכה, בתוך גוש של חומר כל אטום יושב במקום שממזער את האנרגיה של המערכת. בחדר נקי מאוד, כל פיסת ביגוד מקופלת וערומה במגירה. בניגוד לכך, לחומר בטמפרטורה גבוהה, או לחדר מבולגן, יש אנתרופיה גבוהה. כשמדובר בחומר חם, האטומים יכולים לעוף לכל כיוון. בחדר שינה מבולגן, חולצות ומכנסיים יכולים להיזרק בכל פינה בחדר. האנתרופיה של מערכת מוגדרת כלוגריתם של מספר המערכים האפשריים של הרכיבים שלה (אטומים עבור חומר; חולצות ומכנסיים עבור חדר מבולגן) שהיו נראים אותו הדבר, עבור צופה מזדמן.
עבור אובייקטים שגרתיים כמו שולחנות, חדרים, או פיסות עופרת, לא מפתיע שאפשר לשייך למערכת אנתרופיה. אנו יודעים ממה המערכות האלה בנויות, וכיצד לספור את המערכים של הרכיבים שמרכיבים אותן. להפתעתם הרבה של פיזיקאים תיאורטיים, התגלה בתחילת שנות ה-70 של המאה הקודמת כי לרשימת המערכות השכיחות האלה בעלות אנתרופיה, אפשר להוסיף גם חורים שחורים.
2. חורים שחורים והתובנה של בקנשטיין
מהו חור שחור? דמיינו שאתם לוקחים גוש של חומר עם מסה מסוימת, M, ומועכים אותו. תיאוריית הכבידה של איינשטיין אומרת שכשאתם מועכים את החומר לאזור מספיק קטן בחלל – בגודל ש ידוע כרדיוס שוורצשילד, RS(M) – האובייקט יהפוך למשהו מסוג חדש, חור שחור. חור שחור הוא גוש של חומר דחוס כל כך שאפילו אור לא יכול לברוח מפני השטח שלו, או מאופק האירועים שלו. לכן, מה שמתרחש בתוכו נותר תעלומה לעולם החיצון לרבּות עבורנו! אם אתם רוצים לדעת יותר על המשמעות של “אזור מספיק קטן”, אנו יכולים להראות זאת במשוואה:
כאשר G הוא קבוע הגרביטציה, ו-c היא מהירות האור. זה בסדר אם לא תעקבו אחרי פרטי המשוואה; הנקודה הבסיסית היא שאתם יכולים לשים כמות של מסה M או יותר בכדור ברדיוס קטן יותר מ-RS(M), ואז יתרחש קסם – הוא יהפוך לחור שחור.
אנו מדברים על חומר ממש דחוס. לדוגמה, כדי לדחוס את כדור הארץ לגודל הנדרש כדי שיהפוך לחור שחור, אתם צריכים להקטין את הרדיוס שלו מכ-6,400 קילומטרים לבערך 9 מילימטרים! לשמחתנו, הטבע סיפק לנו דוגמאות של חורים שחורים מהחיים האמיתיים, ולכן איננו צריכים לעבוד קשה כדי ליצור אחד. תוכלו אפילו לראות חור שחור, או, ליתר דיוק, את הסביבה החיצונית שלו. תמונה מרהיבה של חור שחור שנמצא בגלקסיה M87 – חור שחור ענקי ששוקל כמעט פי שבעה מיליארד מהשמש שלנו – צולמה לאחרונה על ידי איגוד טלסקופ אופק האירועים [1]!
כסטודנט בפרינסטון בשנות ה 70- של המאה הקודמת, יעקב בקנשטיין תהה לגבי השאלה החידתית הבאה. צופה מחוץ לחור שחור יכול לראות רק את אופק האירועים – החלק הפנימי של החור השחור מוחבא. התכונות הפיזיקליות של אופק האירועים מאופיינות לגמרי על ידי כמה מספרים בלבד: במקרה הפשוט ביותר, המסה M של החור השחור.
אולם, חשב בקנשטיין, האם לא הייתי יכול ליצור את החור השחור שמסתו M בדרכים שונות רבות? יכולתי ליצור אותו על ידי ציפוף של הרבה פילים, או לחלופין של הרבה וומבָּטים (חיית-כיס אוסטרלית קטנה). מה קרה למידע על האופן שבו החור השחור נוצר? לחור השחור צריכה להיות אנתרופיה!
עבודתו של בקנשטיין – ומאוחר יותר, עבודתם המדויקת יותר של ברדין, קרטר והוקינג – הצליחו להוכיח ללא צל של ספק כי לחורים שחורים אכן יש אנתרופיה. הם היו מסוגלים לכתוב נוסחה לאנתרופיה של חור שחור כתלות במסה שלו, S(M) [2]. אולם הטבע המדויק של המצבים הפיזיקליים שיכלו להרכיב את S(M) נותר תעלומה.
3. סופרים עם הארדי ורמנוג’ן
בואו נשנה לרגע את הנושא, לזוג אחר של גיבורים. אחד הסיפורים הדרמטיים ביותר במתמטיקה של המאה ה-20 הוא זה של הארדי ורמנוג’ן [3]. רמנוג’ן, אדם שלימד את עצמו מתמטיקה גבוהה, ועבד במהלך היום כפקיד בנמל מדרס שבהודו בזמן שערך מחקרים מתמטיים בלילות, שלח מכתבים שתיארו את תוצאותיו לכמה מתמטיקאים ידועים. בסופו של דבר מכתביו נענו על ידי תיאורטיקן ידוע של תורת המספרים מקיימברידג’, ג. ה. הארדי, שכתב על הנוסחאות של רמנוג’ן שנכללו במכתבים:
מבט יחיד עליהן היה מספיק כדי להראות שהן נכתבו על ידי מתמטיקאי ברמה הגבוהה ביותר. הן חייבות להיות נכונות, מאחר שאם הן לא היו נכונות לאף אחד לא היה את הדמיון המתאים לכתוב אותן.
מתוקף כוחן של הנוסחאות האלה, הארדי הביא את רמנוג’ן לקיימברידג’, שם הם קיימו את אחד משיתופי הפעולה המפורסמים ביותר בהיסטוריה של המתמטיקה.
אחת התוצאות המרכזיות שלהם ניתנת להסבר בקלות: נניח שיש לכם 5 תפוזים, ואתם רוצים לחלק אותם בין חברים שונים. בכמה דרכים אתם יכולים לעשות זאת? הנה:
אנו יכולים לראות שישנן שבע דרכים לחלק חמישה תפוזים: לקבוצה אחת של 5, לשתי קבוצות של 4 ו-1, וכן הלאה. אנו אומרים שכמות החלוקות של חמש היא שבע. אם נכתוב את הפונקציה שמקשרת לכל מספר שלם את מספר החלוקות p(n), נוכל לכתוב זאת מחדש כך:
עבור מספרים קטנים (n), כמו 3, 4, או 5, חישוב p(n) הוא קל. אולם מה עם p(100)? אם אתם מתחילים לנסות להבין זאת, תראו שחלוקת המספרים מהר מאוד יוצאת משליטה! אם כך, כיצד נוכל לקבוע אותן?
הארדי ורמנוג’ן הצליחו לעשות זאת על ידי פיתוח תכסיס גאוני שנקרא “שיטת העיגול”. הם הגו נוסחה שמאפשרת להם לקבוע בקירוב את p(n), ובאמצעות הנוסחה הזו אפשר ליצור גרף כמו זה שמופיע באיור 1. בציר x יש לנו את n, בעוד שבציר y יש לנו את דיוק ההערכה שלהם עבור p(n). (חלוקות הן הגיוניות רק עבור מספרים שלמים n, אולם הנוסחה הזו מפיקה את התשובה – ואפשר לצייר אותה – עבור כל הערכים של n).
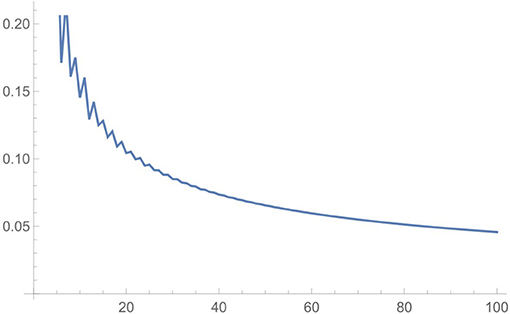
- איור 1 - גרף דיוק ההערכה של הארדי-רמנוג’ן של p(n) לעומת n, עבור ערכי n עד 100.
- המספרים בציר ה-y מראים את אחוז השגיאה של ההערכה [ולכן ערך ה-y של 0.05 שקרוב ל-x = 100 משמעותו שהנוסחה תופסת את p(100) בדיוק של 5%]. קרדיט לתמונה: ג’ון ד. קוק.
4. ומה עם חורים שחורים?
התחלנו עם חורים שחורים, ואז עשינו מעקף לחלוקות של מספרים שלמים. כיצד שני הנושאים האלה קשורים?
כדי לדון בשני הנושאים האלה יחד, ראשית עלינו לדבר על נושא שלישי, שנקרא תורת המיתרים. תורת המיתרים היא אחת התיאוריות שמדענים משתמשים בהן כדי לתאר את הדברים הקטנים ביותר – קטנים אפילו יותר מאטומים – שמרכיבים את היקום. בתורת המיתרים, האובייקטים היסודיים האלה הן לולאות (זעירות) של מיתרים. מצב האנרגיה הנמוך ביותר של לולאת מיתר זעירה הוא חסר תנועה לחלוטין. אתם יכולים להוסיף אנרגיה למיתר כדי ליצור גלים שיכולים לנוע בתדרים שונים ברחבי הלולאה. לדוגמה, באיור 2 (שבו אנו משתמשים במיתר גיטרה במקום בלולאה סגורה של מיתר לשם פשטות האיור), אנו רואים שלגל בעל התדר הנמוך ביותר שאתם יכולים לשים על מיתר יש שיא אחד, בעוד שלתדרים גבוהים יותר (שלעיתים קרובות נקראים הרמוניקות במוזיקה!) יש שניים, שלושה, או יותר שיאים. זה מציע אפשרויות שונות על אותו מיתר, עם תדרים שמתוארים על ידי מספרים שלמים חיוביים.
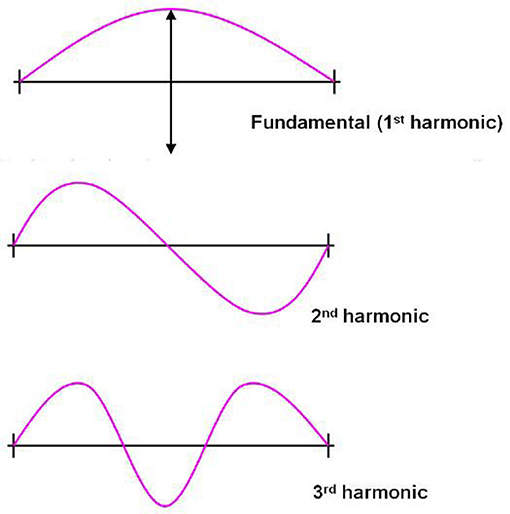
- איור 2 - למיתר גיטרה יש תדר נמוך ביותר, כמו גם הרמוניקות גבוהות יותר שהן כפולות שלמות של התדר הנמוך ביותר הזה.
- קרדיט לתמונה: cronodon.com.
חשוב לומר שאנו יכולים לעורר את המיתר עם שני גלים בתדר הנמוך ביותר, או שלושה, או יותר. כאן, אנו משתמשים בעובדה שהאנרגיות שנמצאות בגלים של תדר נתון במיתר פועלות תחת מכניקת הקוונטים. מיתר גיטרה קלאסי מאפשר פריטה אחת של התדר הנמוך ביותר עם איזושהי אמפליטודה (לכן אפשר להכניס כל כמות אנרגיה לתוך המיתר באותו התדר). אולם מכניקה קוונטית מכמתת את האנרגיה שנמצאת בתדר נתון למקטעים בדידים – ולכן אפשר לקבל מספר שלם (כמו 1.2, 1,729 אבל לא 2.718) של האנרגיה שמקושרת לגל בתדר נתון.
כעת, אנו נמצאים רק צעדים ספורים מהבנת הדרך לחשב אנתרופיה של חור שחור בתורת המיתרים! נסתמך על התצפיות האלה:
1. אנו יכולים לדמיין גלים עם הרבה תדרים שונים שנמצאים על המיתר במקביל. זכרו, כל התדרים הם מספרים שלמים חיוביים, ואנו רוצים לעקוב אחרי מספר “הגושים הקוונטיים” שנמצאים בכל תדר.
2. המחיר האנרגטי של הגושים הקוונטיים האלה עולה עם k. תדרים גבוהים יותר משתמשים ביותר אנרגיה, כאשר התדר ה-k משתמש בפי k אנרגיה מאשר התדר הנמוך ביותר.
3. המשוואה המפורסמת ביותר של איינשטיין אומרת לנו ש:
כלומר, האנרגיה של מיתר מתנודד מופיעה כמסה.
אנו מסיקים שאנו יכולים לחשב את מספר המצבים של מיתרים מאסיביים באנרגיה של N פעמים אנרגיית התדר הנמוך ביותר, באופן הבא, באמצעות השיטה של הארדי-רמנוג’ן שתוארה קודם. אנו יכולים להגיע לרמת אנרגיה N על ידי כל מספר של עירוּרים של התדר הנמוך ביותר n(1), כל מספר n(2) בתדר האנרגיה הנמוך השני, כל מספר n(3) בתדר האנרגיה השלישי, וכן הלאה. אולם כדי לקבל אנרגיה כוללת N, אנו צריכים שיהיו לנו:
אך כל בחירה של קבוצת מספרים [n(1), n(2) וכו’] שמופיעה מצד ימין של הנוסחה, מראה בדיוק את החלוקה של N! מספר המצבים של מיתרים מאסיביים ברמת מסת מיתר N, ניתן על ידי מספר החלוקות של N לשלמים חיוביים, p(N).
הקשר לחורים שחורים הוא מאחר שמיתר מעוּרר מאוד בתורת המיתרים, יכול תיאורטית להיות ממוקם בתוך רדיוס שוורצשילד וליצור חור שחור. מאחר שאנו יודעים את המסה של מצבי מיתר כפונקציה של N, ואנו יודעים את מספר המצבים האלה מ-p(N), אנו יכולים לכתוב נוסחה לאנתרופיה S(M). זה מספק תחזית (נכונה) של כמות האנתרופיה שמתאימה לחורים שחורים במונחים של מספרי חלוקה [4]!
מילון מונחים
אנתרופיה (Entropy): ↑ כמות הבלגן או האקראיוּת שנכנסת לתיאור של מערכת פיזיקלית מסוימת (או, באופן גס, מספר הדרכים שבהן אפשר ליצור אותה).
אופק האירועים (Event Horizon): ↑ פני השטח של חור שחור. אם אתם נמצאים באופק האירועים – או קרוב יותר למרכז – אינכם יכולים לברוח מלהישאב פנימה, אפילו אם אתם קרן אור – האובייקט המהיר ביותר ביקום הידועלפיזיקה המודרנית!
תדר (Frequency): ↑ עבור גל (כמו למשל מים או מיתר מוסט), זהו מספר הפעמים שהגל מגיע לגובה המקסימלי שלו עבור יחידת זמן.
אמפליטודה (Amplitude): ↑ אמפליטודה היא מדד לגובה של שיאים כמו למשל של גלי מים או של מיתרים מוסטים.
הצהרת ניגוד אינטרסים
המחברים מצהירים כי המחקר נערך בהעדר כל קשר מסחרי או פיננסי שיכול להתפרש כניגוד אינטרסים פוטנציאלי.
תודות
העבודה הזו נתמכה בחלקה על ידי הקרן הלאומית למדעים תחת מענק PHY-1720397.
מקורות
[1] ↑ Event Horizon Telescope. Available online at: https://eventhorizontelescope.org (accessed April 24, 2020).
[2] ↑ Hawking, S. 1998. A Brief History of Time. New York, NY: Bantam.
[3] ↑ Kanigel, R. 2016. The Man Who Knew Infinity. New York, NY: Washington Square Press.
[4] ↑ Susskind, L. 2009. The Black Hole War. New York, NY: Back Bay Books.
