ملخص
الجاذبية هي قوة جذب عامة، تحاول أن تُجمّع المواد معًا في صورة كتل. هذا يعني أنه في الأنظمة الفيزيائية المتنوعة، بدءًا من النجوم في نهاية حياتها أثناء حرقها الوقود النووي، ووصولًا إلى سحب الغاز التي تنهار بفعل ثقل جاذبيتها، يمكن أن تكون نقطة النهاية الطبيعية هي تكون ثقب أسود؛ وهو جسم تتجمع فيه المادة بكثافة عالية للغاية؛ لدرجة أن حتى الضوء نفسه لا يستطيع الإفلات من قوة الجاذبية على سطح الثقب، أو أفق الحدث، والثقوب السوداء شائعة، فمجرتنا درب التبانة بها ثقب أسود عملاق في مركزها! ـ وغامضة في الوقت ذاته. نناقش في هذا المقال الأفكار الحالية حول أحد ألغاز الثقوب السوداء؛ ألا وهو: كيف يمكن للمرء تفسير عدد الحالات الفيزيائية المتمايزة (ولكن المتشابهة) التي تختبئ وراء أفق الحدث. يطلق علماء الفيزياء على ذلك اسم إنتروبيا الثقب الأسود.
1. ما المقصود بالإنتروبيا؟
الإنتروبيا في النظام الفيزيائي هي مقياس لمقدار الفوضى أو العشوائية الذي يميز النظام. فالأنظمة التي في حالات خاصة للغاية - مثل أي جزء كبير من المادة العادية عند درجات حرارة شديدة الانخفاض، أو في غرفة نوم نظيفة للغاية، يكون لها مستوى إنتروبيا منخفض. في كلتا هاتين الحالتين يرجع هذا إلى أن مكونات النظام ليس لها خيار بشأن مكان وجودها؛ فعند درجة حرارة منخفضة، في جزء من المادة، تستقر كل ذرة في مكان يقلل من طاقة النظام إلى أقل مستوى ممكن. أما في غرفة نظيفة للغاية، يتم طي كل قطعة ملابس وتخزينها في درج. وعلى النقيض من ذلك، فإن المادة عند درجات الحرارة المرتفعة، أو في غرفة فوضوية، تتسم بالإنتروبيا العالية. يمكن للذرات أن تتنقل في كل اتجاه في المادة الساخنة. ففي غرفة نوم فوضوية مثلًا، يمكن أن تجد القمصان والسراويل القصيرة منتشرة في أنحاء الغرفة شئت أم أبيت. يعرَّف إنتروبيا النظام على أنها لوغاريتم عدد التركيبات المحتملة لمكوناته التي قد تبدو متشابهة تقريبًا من منظور الشخص العادي (الذرات في المادة، والقمصان والسراويل القصيرة في غرفة فوضوية).
بالنسبة للأجسام التقليدية مثل الطاولات أو الغرف أو ألواح الرصاص، فليس من المستغرب أن يتمكن المرء من ربط الإنتروبيا بالنظام. فنحن نعلم ماهية تكوين هذه الأنظمة، وكيفية حساب تركيبات الأجزاء الأساسية منها. وقد تبين في أوائل سبعينيات القرن الماضي أنه يمكن إضافة الثقوب السوداء إلى هذه القائمة من الأنظمة المألوفة التي لها إنتروبيا، الأمر الذي مثل مفاجأة كبيرة لعلماء الفيزياء النظرية.
2. الثقوب السوداء ومنظور BEKENSTEIN
ما المقصود بالثقب السوداء؟ تخيل أن تأخذ كتلة من المادة عند كتلة معينة ثابتة M، وتسحقها. تقول نظرية الجاذبية التي وضعها Einstein إن الجسم عندما ينضغط في حيز صغير بما يكفي من الفضاء — بحجم يعرف باسم نصف قطر شفارتزشيلد RS(M)، يتحول الجسم إلى فئة جديدة نوعيًا من الأجسام الغريبة، إذ يصبح ثقبًا أسود. والثقب الأسود عبارة عن كتلة كثيفة للغاية من المادة لدرجة أن حتى الضوء لا يستطيع الإفلات من قوة الجاذبية على سطحها، أو أفق الحدث؛ وبالتالي فإن ما يحدث داخل الثقب يظل لغزًا يكتنفه الغموض بالنسبة للعالم الخارجي، بما في ذلك نحن العلماء! إذا كنت تريد أن تعرف بمزيد من التفصيل ما يعنيه “حيز صغير بما يكفي”، فيمكننا تناول القانون الآتي:
حيث G ثابت الجاذبية، و c سرعة الضوء. لا بأس إذا لم تتبع تفاصيل هذه المعادلة؛ الفكرة الأساسية هي أنك إذا وضعت مقدارًا من الكتلة M أو أكبر في كرة نصف قطرها أصغر من RS(M)، فسيصبح هذا المقدار ثقبًا أسود.
نحن نتحدث عن مادة كثيفة للغاية. على سبيل المثال، لضغط الأرض إلى الحجم المطلوب لتكوين ثقب أسود، يتعين عليك خفض نصف قطرها الحالي البالغ 4,000 ميل إلى 9 ملليمترات تقريبًا! ومن حسن الحظ أن الطبيعة زودتنا بأمثلة من واقع الحياة على الثقوب السوداء، لذا فنحن لا نحتاج إلى القيام بتكوين ثقب بأنفسنا. في الواقع، يمكنك الآن رؤية ثقب أسود، أو بدقة أكبر، المنطقة المحيطة به. التُقِطت صورة مذهلة للثقب الأسود الموجود في المجرة M87 — وهو ثقب أسود ضخم جدًا، وزنه أكبر من وزن شمسنا بسبعة مليارات مرة - مؤخرًا بواسطة الجهود المشتركة لتليسكوب أفق الحدث [1]!
بحكم كون Jacob Bekenstein طالب دراسات عليا في جامعة Princeton في سبعينيات القرن الماضي، فكر Jacob في التساؤل المحير التالي. يمكن للناظر من خارج الثقب الأسود رؤية أفق الحدث فقط، بينما يكون يكون الجزء الداخلي مخفيًا. وتوصّف الخصائص الفيزيائية لأفق الحدث بالكامل بعدد قليل من الأرقام: في أبسط الحالات، الكتلة M للثقب الأسود.
لكن، حسب اعتقاد Bekenstein، ألم يكن ممكنًا تكوين الثقب الأسود ذي الكتلة M بعدة طرق مختلفة؟ كان يمكن تكوينه من خلال إلقاء العديد من الأفيال في الثقب، أو بدلًا من ذلك، العديد من حيوانات الومبت (الدببة الاسترالية). لكن ما مصير المعلومات المتعلقة بكيفية تكوين الثقب الأسود؟ يجب أن يكون للثقب الأسود إنتروبيا!
ولقد نجح عمل Bekenstein — وما تلاه من أعمال أكثر دقة للعلماء Bardeen، وCarter، وHawking — في إثبات أن الثقوب السوداء لها بالفعل قيمة إنتروبيا بما لا يدع مجالًا للشك، وكانوا قادرين على وضع معادلة لإنتروبيا الثقب الأسود كدالة لكتلته S(M) [2]. لكن الطبيعة الدقيقة للحالات الفيزيائية التي يمكن أن تفسر المعادلة S(M) ظلت غامضة.
3. العد مع قصة HARDY وRAMANUJAN
دعونا نغير الموضوع محل الدراسة سريعًا، إلى زوج آخر من الأبطال. من أكثر القصص الدرامية إثارة للاهتمام في الرياضيات في القرن العشرين هي قصة HARDY وRAMANUJAN [3]. حيث أرسل Ramanujan – الذي علم نفسه ذاتيًا الرياضيات العليا ويعمل كاتبًا في وظيفة نهارية في ميناء Madras إلى جانب إجراء أبحاث في مجال الرياضيات ليلًا في الوقت نفسه –رسائل يصف فيها نتائجه إلى عدد قليل من علماء الرياضيات المعروفين. وفي نهاية المطاف، أجاب عن رسائله واضع نظريات الأعداد الشهير G.H. Hardy بجامعة Cambridge الذي قال عن المعادلات التي أوردها Ramanujan في رسائله:
نظرة واحدة على هذه المعادلات تكفي لتبرهن على أنه لا يمكن كتابتها إلا بواسطة عالم رياضيات من الطراز الرفيع. ولابد أن تكون صحيحة، لأنه إذا لم تكن صحيحة، فلن يكون لدى أحد المخيلة اللازمة لاختراعها.
بناءً على قوة هذه المعادلات، أحضر العالم Hardy العالم Ramanujan إلى جامعة Cambridge، حيث اشتركا في واحدة من أشهر عمليات التعاون في تاريخ الرياضيات.
ومن السهل تفسير إحدى النتائج المركزية لها: فلنفترض أن لديك 5 برتقالات، وكنت ترغب في تقسيمها بين عدد من الأصدقاء. كم عدد الطرق التي يمكن أن تتخيلها لتقسيمها؟ حسنًا:
لذلك نرى أن هناك 7 طرق لتقسيم 5 برتقالات: في مجموعة واحدة من 5، مجموعتين من 4 و 1، وما إلى ذلك. وعليه، نقول إن عدد تقسيمات الرقم 5 هو 7. إذا كتبنا دالة تربط كل عدد صحيح بعدد التقسيمات p(n)، فيمكننا إعادة صياغة هذا كالتالي:
للأعداد الصغيرة (n)، مثل 3، أو 4، أو 5، يكون حساب p(n) سهلًا. ولكن ماذا عن p(100)؟ إذا بدأت في محاولة إيجاد ذلك، فسترى أن أرقام الأقسام تزداد بسرعة كبيرة خارج نطاق السيطرة! فكيف لنا أن نحددها؟
لقد نجح Hardy وRamanujan في القيام بذلك من خلال تطوير خدعة بارعة تسمى “طريقة الدائرة”؛ لقد توصلا إلى معادلة سمحت لهما بتحديد p(n) تقريبًا وباستخدام هذه المعادلة، يمكن إنشاء رسم بياني مثل الوارد في الشكل 1. فعلى محور السينات لدينا n، بينما على محور الصادات لدينا دقة تقديرهما لقيمة p(n). (تكون التقسيمات منطقية فقط للأعداد الصحيحة n، لكن معادلتهما توضح إجابة لجميع قيم n، ويمكن تمثيلها بيانيًا).
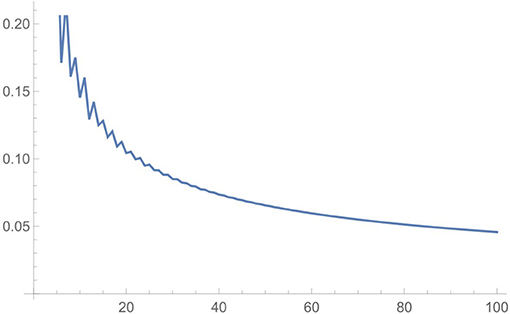
- شكل 1 - رسم بياني لدقة تقدير Hardy-Ramanujan لقيم p(n) مقابل n، لقيم n تصل إلى 100.
- تُظهر العلامة الموجودة على محور الصادات الخطأ الجزئي للتقدير (لذا فإن قيمة الصادات البالغة 0.05 بالقرب من س = 100 تعني أن المعادلة تضع p(100) بدقة تبلغ حوالي 5%). حقوق الصورة: John D. Cook.
4. ماذا عن الثقوب السوداء؟
بدأنا بالحديث عن الثقوب السوداء، ثم تطرقنا في حديثنا إلى التقسيمات في الأعداد الصحيحة الموجبة. ما العلاقة بين هاتين المسألتين؟
للجمع بين هذين الموضوعين معًا، يتعين علينا أولًا التحدث عن موضوع ثالث، يُسمى نظرية الأوتار، وهي إحدى النظريات التي يستخدمها العلماء لوصف أصغر الأشياء التي يتألف منها الكون؛ حتى ما هو أصغر من الذرات. في نظرية الأوتار، هذه الأجسام الأساسية هي أوتار حلقية (صغيرة). وتكون أقل حالة طاقة في حلقة وترية صغيرة هي السكون التام. يمكنك أيضًا إضافة طاقة إلى الأوتار لتكوين موجات يمكنها السفر بترددات مختلفة حول الحلقة. على سبيل المثال، من الشكل 2 (حيث نستخدم وتر جيتار بدلًا من حلقة مغلقة من الأوتار لسهولة التوضيح)، نرى أن أقل موجة ترددية يمكنك وضعها على الوتر لها قمة واحدة، في حين أن الترددات الأعلى (تُسمى غالبًا التوافقيات الأعلى في الموسيقى!) يكون لها قمتين أو ثلاث قمم أو أكثر. هذا يسمح بوجود موجات مختلفة متعددة على الوتر، ذات ترددات ممثلة بأعداد صحيحة موجبة.
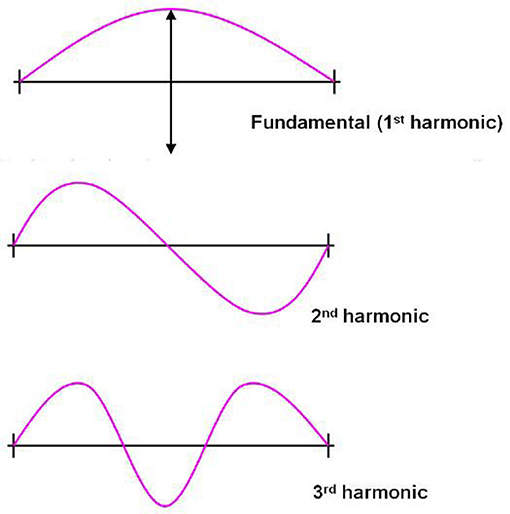
- شكل 2 - يحتوي وتر الجيتار على أدنى تردد للاهتزاز، بالإضافة إلى التوافقيات الأعلى التي تعد مضاعفات صحيحة لهذا التردد الأدنى.
- حقوق الصورة لموقع cronodon.com.
الأهم من ذلك أنه يمكننا أيضًا استثارة الوتر بموجتين بأقل تردد ممكن، أو ثلاث موجات أو أكثر. هنا نستخدم حقيقة أن الطاقات الموجودة في موجات ذات تردد معين على الوتر تخضع لميكانيكا الكم. يسمح وتر الجيتار الكلاسيكي للشخص أن ينقر على أدنى تردد بأي سعة (وبالتالي وضع أي كمية من الطاقة في الوتر عند هذا التردد). لكن ميكانيكا الكم تحدد كمية الطاقة الموجودة عند تردد معين في قطع منفصلة – بحيث تكون طاقة كل قطعة تساوي أحد مضاعفات الأعداد الصحيحة (مثل 1.2، أو 1.72، ولكن ليس 2.718) للطاقة المصاحبة لموجة عند تردد معين.
الآن، نحن على بعد خطوات قليلة فقط من معرفة كيفية حساب إنتروبيا الثقب الأسود في نظرية الأوتار! إننا نعتمد على الملاحظات التالية:
- يمكننا تخيل وجود موجات ذات ترددات عديدة مختلفة في نفس الوقت على الوتر. تذكر أن جميع الترددات أعداد صحيحة موجبة، ونريد أن نتتبع العدد الذي يمثل ”القطع الكمية” الموجودة عند كل تردد.
- تزداد تكلفة الطاقة لهذه القطع الكمية مع زيادة k. فالترددات الأعلى تستهلك طاقة أكثر، حيث يستخدم التردد رقم kth طاقة أكبر من الطاقة التي يتسخدمها أقل تردد بعدد k من المرات.
- تخبرنا المعادلة الأكثر شهرة للعالم Einstein بأن
أي أن طاقة الوتر المهتز تظهر في شكل كتلة.
نستنتج من ذلك أنه يمكننا حساب عدد حالات الوتر الضخم عند مستوى طاقة أكبر من أقل وضع طاقة بعدد N من المرات، بالطريقة التالية، باستخدام طريقة Hardy-Ramanujan الموضحة أعلاه. يمكننا الوصول إلى مستوى الطاقة N من خلال الحصول على أي عدد من الاستثارات ذات التردد الأدنى n(1)، وأي رقم n(2) في ثاني أدنى تردد، وأي رقم n(3) مع التردد الثالث، وهكذا. ومع ذلك، للوصول إلى إجمالي الطاقة n يجب أن يكون لدينا
ولكن كل خيار من مجموعة الأرقام [n(1)، وn(2)، إلى آخره] على الجانب الأيمن من هذه المعادلة يعرض أحد تقسيمات n بدقة! يُعطى عدد حالات الوتر الضخم عند مستوى كتلة الوتر n من خلال عدد تقسيمات n في أعداد صحيحة موجبة، p(N).
هذا يرتبط بالثقوب السوداء لأن الوتر المستثار للغاية والمتحرك في نظرية الأوتار يمكن جعله من الناحية النظرية يقع داخل نصف قطر شفارتزشيلد ويشكل بذلك ثقبًا أسود. نظرًا لأننا نعرف كتلة حالات الوتر في شكل دالة n، ونعرف عدد حالات الوتر هذه من p(n)، يمكننا إنتاج معادلة للإنتروبيا S(M)؛ وهذا يقدم تنبؤًا (صحيحًا) لإنتروبيا الثقوب السوداء المناسبة بدلالة أعداد التقسيمات [4]!
مسرد للمصطلحات
الإنتروبيا (Entropy): ↑ مقدار الفوضى أو العشوائية التي تدخل في تحديد نظام مادي معين (أو تقريبًا، عدد الطرق التي يمكن صنعه بها).
أفق الحدث (Event Horizon): ↑ سطح الثقب الأسود. إذا كنت في أفق الحدث - أو أقرب إلى المركز - فلا يمكنك الهروب من جاذبية الثقب، حتى ولو كنت شعاعًا ضوئيًا وهو أسرع جسم متحرك معروف في الفيزياء الحديثة!
التردد (Frequency): ↑ بالنسبة للموجة (على سبيل المثال، موجه من الماء، أو إزاحة في وتر) ، التردد هو عدد المرات التي تصل فيها الموجة إلى أقصى ارتفاع لها لكل وحدة زمنية.
السعة (Amplitude): ↑ السعة هي قياس ارتفاع القمم في موجات الماء أو موجات إزاحة الأوتار على سبيل المثال.
إقرار تضارب المصالح
يعلن المؤلفون أن البحث قد أُجري في غياب أي علاقات تجارية أو مالية يمكن تفسيرها على أنها تضارب محتمل في المصالح.
شكر وتقدير
دُعِم هذا العمل جزئيًا بواسطة مؤسسة العلوم الوطنية بموجب المنحة PHY-1720397.
المراجع
[1] ↑ Event Horizon Telescope. Available online at: https://eventhorizontelescope.org/ (accessed April 24, 2020).
[2] ↑ Hawking, S. 1998. A Brief History of Time. New York, NY: Bantam.
[3] ↑ Kanigel, R. 2016. The Man Who Knew Infinity. New York, NY: Washington Square Press.
[4] ↑ Susskind, L. 2009. The Black Hole War. New York, NY: Back Bay Books.
