Abstract
Materials science investigates the structure and properties of different materials. One of these materials is the crystal. Crystals are solid materials with building blocks (atoms, ions, or molecules) that are arranged in a highly organized manner. Salt, quartz, and diamonds are examples of crystals. In ordinary crystals, these building blocks are organized in a repeating pattern in all directions. In contrast, in special crystals called quasi-crystals, the building blocks are organized in a non-repeating manner. The discovery of quasi-crystals created a revolution in the science of crystallography and changed our most basic definition of a crystal. Since their discovery, many hundreds of quasi-crystals have been found. Some of these quasi-crystals have unique physical properties and are useful for a variety of different applications.
Professor Shechtman won the Nobel Prize in Chemistry in 2011 for the discovery of Quasi-Crystals.
Interviewed and co-written by Noa Segev, graduate of the Grand Technion Energy Program, Technion, Israel Institute of Technology, Haifa, Israel.
How I Became a Materials Scientist
When I was 7 years old, my grandfather bought me an extraordinary present—a magnifying glass! It made me very happy and I started walking around the city of Ramat Gan (in Israel) with this magnifying glass. I looked at everything I could find—flowers, bugs, sand, and many other small things. During this process I fell in love with the world of small things. A few years later, when I was in the fifth grade, a microscope was delivered to our school. Week after week, I asked my teacher to bring the microscope to our class. Eventually he did, and he invited me to be the first to look through it. We looked at a leaf, and I could see the motion of the chlorophyll, a small molecule inside the leaf responsible for its green color. Since then I could not leave the microscope. Years later, during my studies at the Technion (Israel Institute of Technology), an exceptionally strong microscope arrived at our facility, called a transmission electron microscope (TEM). I fell in love with this microscope because it allowed me to realize my scientific curiosity for the world of small things. I soon specialized in operating this microscope, and by using it I discovered a new type of material which, many years later, earned me a Nobel prize.
The Discovery of Quasi-Crystals
In 1981, I went to the United States to study aluminum-based materials for use in airplanes. Initially, I worked on an alloy of aluminum and iron and discovered a new phase—a special arrangement of the atoms in this alloy. I wanted to study this arrangement, but it was unstable. So instead, I prepared various alloys with aluminum and manganese, which were stable. I started preparing alloys of aluminum-manganese in different concentrations. Some of these alloys were useful for aviation applications and some were not, but I still prepared them because of my scientific curiosity. I studied all of these aluminum-manganese alloys using the TEM. I call the TEM “the king of microscopes,” since it is a very powerful tool with amazing capabilities. TEM allows us to see the way the atoms are arranged in different materials.
On Thursday, April 8th 1982, I studied one of my alloys using the TEM and I saw a very special pattern on the screen. We call the pattern made when electrons interact with a solid obstacle, like a crystal, a diffraction pattern (Figure 1, left). I immediately recognized that there was something unusual in the diffraction pattern, and thus in the structure of this material, which we now call “quasi-crystal,” and so I wrote, “10-fold???” in my laboratory notebook (Figure 1, right, line 6 in brackets). I will now explain what was so special about this pattern, the meaning of the remark in my notebook, and why it revolutionized the world of crystallography.

- Figure 1 - The discovery of the first quasi-crystal.
- (Left) Diffraction pattern of the aluminum-manganese quasi-crystal that I discovered in 1982. The scattered pattern of the dots shows us the arrangement of the atoms from which this material is built. (Right) My laboratory notebook, documenting my surprise over this discovery (scan 1725, line 6). Credit: Dan Shechtman.
Crystals—Before and After the Discovery
The science of crystallography (the study of crystals) started in 1912, with a German physicist named Max von Laue. Von Laue was the first to send X-rays through a crystal, and he saw that the atoms formed an ordered diffraction pattern. In the same year, two father-and-son English physicists, the Braggs, developed a mathematical equation describing the experimental phenomenon that von Laue observed. That is how crystallography emerged as a new scientific field. After the birth of crystallography, many thousands of crystals were studied and they all exhibited two common properties: they were ordered (not random) and periodic (exhibiting a repeating pattern) (Figure 2). Because of all these observations, the definition of a crystal became “a solid material in which the atoms are arranged in a fixed, repeating structure.” Well-known examples of crystals are salt grains, quartz stones, and diamonds, but most metals, such as copper, aluminum, and iron, are also crystals. Classical crystals also have a property called rotational symmetry. Due to mathematical rules describing the internal arrangement of crystals it was found that crystals can have rotational symmetries from different types, called “orders” (i.e., order 1, 2, 3, 4, or 6; see Figure 2, center, for a demonstration of a rotational symmetry of order 4) and not of other orders (e.g., order 5 or 10).
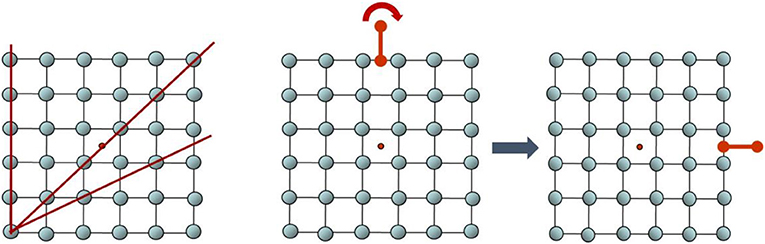
- Figure 2 - Order, periodicity, and rotational symmetry.
- (Left) A simple, ordered, periodic crystal. The dots, representing the crystal’s atoms, are arranged in an ordered, non-random manner. The crystal is also periodic, meaning that, if you choose one direction (red lines) and proceed from one dot to the next, the distance between every two dots on the line is identical. You can also see periodicity if you choose a square containing four atoms and duplicate it in all directions, because you will get exactly the same structure. (Center) A structure with 4-fold rotational symmetry. Imagine yourself holding the red handle and turning the structure in 90° clockwise. Now the handle is to the right (as seen in the square on the right). Without the red handle, the whole structure looks exactly the same before and after the rotation. In this crystal, the structure repeats itself in every 90° rotation. This is called 4-fold symmetry because, for every four such rotations, we complete a 360° turn and all the dots return to their original locations. Credit: Dan Shechtman.
Seventy years after the birth of crystallography, I found a crystal that is ordered but is not periodic. In order to better understand what this means, look at the left side of Figure 3. You can see widening circles of dots (blue, yellow, and red) around the big central dot. Each circle is composed of 10 dots, resembling a flower with 5 pairs of opposite leaves (point 1 is the partner of point 6, point 2 is the partner of point 7, etc.). If you measure the distance from the center to the first circle, you will see that it is not half the distance between the center and second circle (blue and yellow lines in Figure 3 on the right). Also, the distance between the center and the first circle is not one-third the distance between the center and the third circle (blue and red lines in Figure 3 on the right). This means that we cannot take one circle and duplicate it in equal distances from the center and get the crystal that I saw, which means that the crystal is non-periodic. But we can use mathematics to describe the distances between the center and the widening circles, which means that the crystal structure is not random, but is ordered (Here is a puzzle: can you find the connection between my crystal and the famous Mona Lisa painting? The answer is at the end of this article).
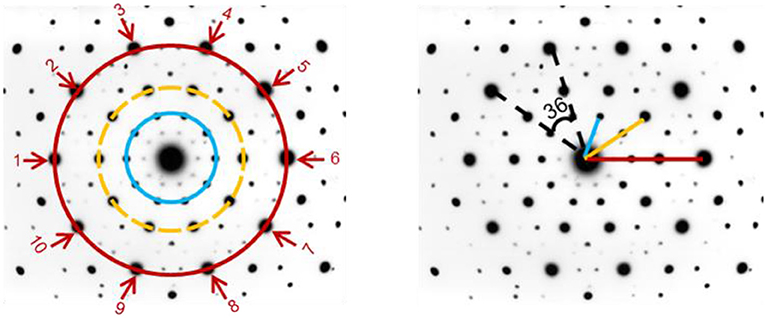
- Figure 3 - Diffraction pattern of a quasi-crystal.
- (Left) The diffraction pattern appears as widening circles (blue, yellow, and red), each of which is composed of 10 dots arranged in pairs that are across from each other (dot 1 is a partner of dot 6, for example). (Right) The angle between any two nearby dots on the same circle is 36° (dashed black lines), meaning that one rotation of 36° from the center makes the pattern look the same as before it was rotated. Ten such rotations will bring all the dots to their original locations; so this pattern is called 10-fold rotational symmetry. You can also see that the distance between the center and the first circle (blue line) is not half the distance between the center and the second circle (yellow line), and it is not one-third the distance between the center and third circle (red line). This means that this pattern is not periodic.
Notice how the dots in Figure 3 (left) are arranged with identical distances from each other on the circle. Since there are 10 equally spaced dots in the circle, if you put an axis at the center of the circle and turned it in 36° (360°/10 = 36°) in either direction, you would get the exact same picture as before the turn. We call this 10-fold rotational symmetry. Since 10- or 5-fold rotational symmetry do not occur in periodic crystals (for more information, see this link), this crystal was clearly not periodic. This is why I wrote, “10-fold???” in my notebook, as an abbreviation of “10-fold rotational symmetry.” I added the three question marks because I knew that a crystal with 10-fold symmetry had not been seen before.
To summarize, I found a crystal which contradicted the classical definition of a crystal and was considered “forbidden” by the physical laws of that time. This situation meant that there were two options: either there was another explanation to the phenomenon that I witnessed, which did not contradict the existing definitions, or the existing definitions needed to be updated to include the crystal that I discovered. In the next section I will describe how the scientific community became convinced that a new definition for a crystal was required.
The Discovery of Quasi-Crystals Was Criticized Before It Was Accepted
Two years after the discovery, I published two papers on this topic with my colleagues [1, 2]. Thousands of researchers around the world joined us and started studying quasi-crystals (now there are more than 10,000 published papers about quasi-crystals). But a strong opposition also arose, led by the great American scientist Linus Pauling, who won the Nobel prize twice. Pauling attacked me personally and even said, “there are no quasi-crystals, there are quasi-scientists.” Pauling and his supporters claimed that what I saw in the microscope was a phenomenon called twins (Figure 4). This is a phenomenon of crystals in which two crystals are coupled to each other. Each crystal is ordered and periodic, and because of the couples, the crystal appears to have a 5-fold symmetry.

- Figure 4 - Twin crystals exhibiting a 5-fold symmetry.
- (Left) An aluminum-iron crystal made from five twin crystal couples. Every “leaf” is an ordered, periodic crystal and every two coupled crystals (like the ones marked in red) are called twins and are mirror images of one another. (Right) A diffraction pattern of a twin crystal. You can see that the resulting pattern is similar to that of the quasi-crystal (Figure 1). This image is the sum of the diffraction patterns of each individual crystal. The red circles in the figure mark the diffraction pattern of one crystal out of the 10 adjacent crystals. You can see that the pattern is ordered and periodic, so it satisfies the classical definition of a crystal.
I checked right away to see if there were twins in my crystals, but I did not find any twins and I was certain of my original result. I knew that I had identified a new phenomenon and discovered a new material. Pauling’s opposition to my findings proceeded for 10 years! After Pauling’s death in 1994, most of the opposition to my scientific discovery faded away and the door opened to its full acceptance. The recognition of my discovery resulted in a new definition for a crystal, and it also inevitably shed new light on the science of crystallography. Of the hundreds of quasi-crystals discovered after my own discovery, some of them exhibit useful properties, such as resistance to deterioration, and interesting electrical properties that change as a function of temperature. A few products using quasi-crystals have been produced, such as Sitram’s non-stick coating for pans, and Sandvik’s strengthened stainless steel.
Recommendations for Young Scientists
If you want to become a scientist, you need to develop two qualities. First, you need to be people of the big world of science. You need to have a broad knowledge of different fields, such as mathematics, physics, chemistry, biology, computers and you also need to know what has already been discovered, and what is “allowed” or “prohibited” according to current theories. In the case of my discovery, I knew that 5-fold symmetry was “prohibited” by the then-accepted definition of crystals and was observed only in twin crystals up until then.
But knowing the existing theories is not enough to make you a successful scientist. You also need to develop an expertise. Find something that you enjoy doing, something that you are good at and that interests you—and become an expert in it. I developed expertise with the TEM and, at the time, there were only a few people who knew how to operate it as well as I did. This was my advantage and what allowed me to remain confident in my results, even in the face of Pauling’s harsh criticism.
In conclusion, remember that life presents us with many opportunities and we need to know how to utilize them. Also, remember that life is built from a variety of rich elements. When I am asked about the happiest moments of my life, I reply that these times were the births of my wife and my four children and 12 grandchildren. I hope that you will also experience the wonder of creating life and understanding the world, and I wish you the best of luck in your journey.
Answer to the Riddle From “What Is a Crystal”
In the crystal that I found, the ratio between the diameters of the widening circles (Figure 3, right) is the golden ratio—an irrational number with a value equal to about 1.618. The same golden ratio is found in the face of Mona Lisa—the most famous painting by Leonardo da Vinci. The golden ratio produces a pleasing experience of beauty for the observer. Can you notice the beauty in the diffraction pattern that I discovered?
Glossary
Transmission Electron Microscope (TEM): ↑ A microscope that uses a beam of electrons to penetrate the material being examined. The electrons produce a diffraction pattern that shows the atomic structure of the material.
Alloy: ↑ A material made from at least two elements, in which one or more is a metal.
Phase (Crystal): ↑ A certain state of a material. Many times we speak about phases in the context of the state of the material—gas, liquid, solid, or plasma, but here we mean a specific arrangement in space of the atoms constituting the material.
Crystal: ↑ A solid material with building blocks (atoms, ions, or molecules) that are arranged in space in an ordered manner.
Diffraction: ↑ A phenomenon in which light or electrons are scattered when they interact with an obstacle, such as a crystal or other solid material.
Quasi-Crystals: ↑ Crystals with building blocks that are arranged in space in a non-periodic manner, meaning they are not duplicated in all directions in a repeating pattern.
Crystallography: ↑ A scientific field that investigates the spatial arrangement of atoms in solids, among which are crystals.
Order: ↑ An organized pattern that is not random.
Periodicity: ↑ A repeating pattern that is duplicated again and again (in time or space).
Rotational Symmetry: ↑ A pattern repeating itself by rotations around a central axis.
Conflict of Interest
The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
[1] ↑ Shechtman, D., and Blech, I. A. 1985. The microstructure of rapidly solidified Al6Mn. Metall. Trans. A 16:1005–12. doi: 10.1007/BF02811670
[2] ↑ Shechtman, D., Blech, I., Gratias, D., and Cahn, J. W. 1984. Metallic phase with long-range orientational order and no translational symmetry. Phys. Rev. Lett. 53:1951–4. doi: 10.1103/PhysRevLett.53.1951
