Résumé
La science des matériaux étudie la structure et les propriétés de différents matériaux. Les cristaux font partie de cette catégorie. Ce sont des matériaux solides dont les éléments constitutifs (atomes, ions ou molécules) sont agencés de manière hautement organisée. Le sel, le quartz ou les diamants en sont des exemples. Dans les cristaux ordinaires, les éléments constitutifs sont organisés selon un motif répété dans toutes les directions. En revanche, dans des cristaux particuliers appelés « quasi-cristaux », les éléments constitutifs sont organisés de manière non répétitive. La découverte des quasi-cristaux a été à l’origine d’une révolution en cristallographie et a changé notre définition de ce qu’est un cristal. Depuis leur découverte, plusieurs centaines de quasi-cristaux ont été identifiés. Certains d’entre eux possèdent des propriétés physiques uniques et sont utilisés dans un grand nombre d’applications.
Le Professor Shechtman a obtenu le prix Nobel de chimie en 2011 pour sa découverte des quasi-cristaux.
Intervieweuse et co-autrice : Noa Segev, diplômée du programme Grand Technion Energy, Technion (Institut de technologie d’Israël), Haïfa, Israël.
Comment je suis devenu un scientifique des matériaux
Quand j’avais 7 ans, mon grand-père m’a offert un cadeau extraordinaire : une loupe ! J’en étais ravi et je l’emportais dans toutes mes balades dans la ville de Ramat Gan (en Israël). Avec ma loupe, j’étudiais tout ce qui croisait mon chemin : les fleurs, les insectes, les grains de sable et tout un tas d’autres petites choses. En faisant ça, je suis tombé amoureux du monde des petites choses. Quelques années plus tard, quand j’avais dix ans environ, notre école a reçu son premier microscope. Chaque semaine, je demandais à mon professeur d’apporter le microscope dans notre classe. Finalement, il l’a fait et m’a invité à être le premier à regarder dedans. Nous avons observé une feuille, et j’ai pu voir le mouvement des chloroplastes, ces petites structures des cellules végétales qui contiennent la chlorophylle, une molécule responsable de la couleur verte des feuilles. À partir de ce moment, je n’ai plus pu quitter le microscope. Des années plus tard, pendant mes études au Technion (Institut de technologie d’Israël), un microscope exceptionnellement puissant – un microscope électronique à transmission (MET) – est arrivé dans notre laboratoire. J’en suis tombé amoureux car il m’a permis d’assouvir ma curiosité scientifique pour le monde des petites choses. Je me suis rapidement spécialisé dans son utilisation et j’ai ainsi découvert un nouveau type de matériau qui, de nombreuses années plus tard, m’a valu un prix Nobel.
La découverte des quasi-cristaux
En 1981, je suis allé aux États-Unis pour étudier les matériaux à base d’aluminium utilisés dans la fabrication des avions. Au départ, j’ai travaillé sur un alliage d’aluminium et de fer, et j’ai découvert une nouvelle phase, c’est-à-dire une disposition particulière des atomes dans cet alliage. Je voulais l’étudier, mais elle était instable. J’ai donc préparé différents alliages avec de l’aluminium et du manganèse dans des proportions différentes, qui, eux, étaient stables. Certains d’entre eux étaient utiles pour les applications aéronautiques et d’autres ne l’étaient pas, mais je les ai quand même préparés, simplement parce que j’étais curieux. J’ai étudié tous ces alliages d’aluminium-manganèse en utilisant le MET. À mes yeux, le MET est le roi des microscopes, car c’est un outil très puissant avec des capacités incroyables. Le MET nous permet de voir la manière dont les atomes sont disposés dans différents matériaux.
Le jeudi 8 avril 1982, j’étudiais l’un de mes alliages en utilisant le MET et j’ai vu un motif très spécial sur l’écran. Nous appelons le motif créé lorsque des électrons interagissent avec un obstacle solide, comme un cristal, un « motif de diffraction » (Figure 1, à gauche). J’ai tout de suite vu qu’il y avait quelque chose d’inhabituel dans ce motif de diffraction. En décrivant la structure de ce matériau, que nous appelons maintenant « quasi-cristal », j’ai noté dans mon carnet de laboratoire « 10-fold ??? » (« ordre 10 ??? ») (Figure 1, à droite, à la ligne 6, entre parenthèses). Je vais t’expliquer maintenant ce qui était si particulier dans ce motif, la signification de la remarque dans mon carnet, et pourquoi cette découverte a révolutionné le monde de la cristallographie.

- Figure 1 - La découverte du premier quasi-cristal.
- (À gauche) Figure de diffraction du quasi-cristal aluminium-manganèse que j’ai découvert en 1982. La dispersion des taches indique la manière dont sont répartis les atomes du matériau. (À droite) Mon cahier de laboratoire, montrant ma surprise de cette découverte (ligne 6). Crédit images : Dan Shechtman.
Les cristaux avant et après la découverte
La cristallographie a vu le jour en 1912 grâce au physicien allemand Max von Laue. Il a été le premier à envoyer des rayons X à travers un cristal et a vu que les atomes formaient un motif de diffraction ordonné. La même année, deux physiciens anglais, un père et son fils, William Henry et William Lawrence Bragg, ont développé une équation mathématique décrivant le phénomène expérimental observé par Max von Laue.
Après la naissance de la cristallographie, plusieurs milliers de cristaux ont été étudiés et tous ont présenté deux propriétés communes : ils étaient ordonnés (non aléatoires) et périodiques (ils présentaient un motif qui se répète). En raison de toutes ces observations, un cristal a été défini comme un matériau solide dans lequel les atomes sont disposés dans une structure fixe et répétitive. Des exemples bien connus de cristaux sont les grains de sel, les pierres de quartz et les diamants, mais la plupart des métaux tels que le cuivre, l’aluminium et le fer forment également des cristaux. Les cristaux classiques ont une propriété appelée « symétrie de rotation ». En raison des règles mathématiques décrivant l’arrangement interne des cristaux, on a établi que les cristaux pouvaient avoir des symétries de rotation de différents types, appelées « ordres » (par exemple, l’ordre 1, 2, 3, 4 ou 6 ; la Figure 2 au centre représente une symétrie de rotation d’ordre 4, mais pas d’ordre 5 ou 10).
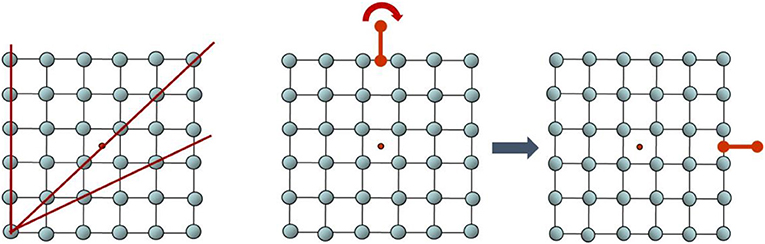
- Figure 2 - Ordre, périodicité et symétrie de rotation.
- (À gauche) Un cristal simple, ordonné et périodique. Les points, représentant les atomes du cristal, sont disposés de manière ordonnée et non aléatoire. Le cristal est également périodique, ce qui signifie que si tu choisis une direction (ligne rouge) et que tu te déplaces d’un point à un autre, la distance entre chaque paire de points sur la ligne est toujours la même. Tu peux également observer la périodicité si tu choisis un carré contenant quatre atomes et que tu le dupliques dans toutes les directions, car tu obtiendras exactement la même structure. (Au centre) Une structure avec une symétrie de rotation d’ordre 4. Imagine que tu tiens la poignée rouge et que tu tournes la structure de 90 ° dans le sens des aiguilles d’une montre. Maintenant, la poignée est à droite (comme on peut le voir dans le carré de droite). Sans la poignée rouge, toute la structure semble identique avant et après la rotation. Dans ce cristal, la structure se répète à chaque rotation de 90 °. Cela s’appelle une symétrie d’ordre 4, car après quatre rotations de ce type, nous effectuons un tour complet de 360° et tous les points reviennent à leur emplacement d’origine. Crédit : Dan Shechtman.
Soixante-dix ans après la naissance de la cristallographie, j’ai découvert un cristal qui était ordonné mais non périodique. Pour mieux comprendre ce que cela signifie, regarde le panneau gauche de la Figure 3. Tu peux voir des cercles concentriques de points (bleus, jaunes et rouges) autour du grand point central. Chaque cercle est composé de 10 points, ressemblant à une fleur avec 5 paires de pétales opposés (le point 1 est le partenaire du point 6, le point 2 est le partenaire du point 7, etc.). Si tu mesures la distance entre le centre et le premier cercle, tu verras qu’elle n’est pas la moitié de la distance entre le centre et le deuxième cercle (lignes bleues et jaunes dans la Figure 3 à droite). De même, la distance entre le centre et le premier cercle n’est pas d’un tiers de la distance entre le centre et le troisième cercle (lignes bleues et rouges dans la Figure 3 à droite). Cela signifie que nous ne pouvons pas prendre un cercle et le dupliquer à des distances égales du centre pour obtenir le cristal que j’ai vu, et cela veut dire que le cristal est non périodique. Cela dit, nous pouvons quand même utiliser les mathématiques pour décrire les distances entre le centre et les cercles concentriques, ce qui signifie que la structure cristalline n’est pas aléatoire, mais ordonnée. (Voici une devinette : peux-tu trouver un lien entre mon cristal et la célèbre peinture de la Joconde ? La réponse se trouve à la fin de cet article).
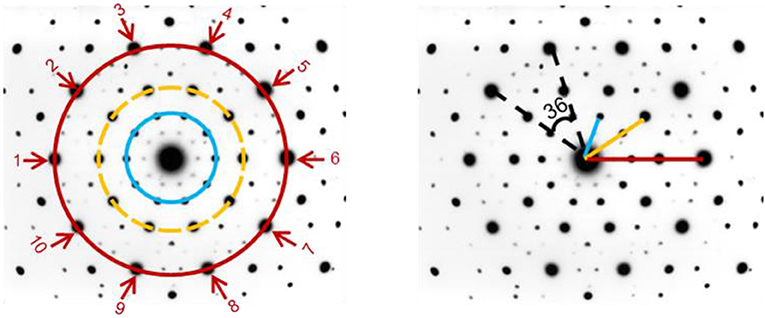
- Figure 3 - Figure de diffraction d’un quasi-cristal.
Vois-tu comment les points dans la Figure 3 (à gauche) sont disposés à intervalles réguliers les uns des autres sur le cercle (la distance entre deux points adjacents est constante pour un cercle donné) ? Comme il y a 10 points également espacés sur le cercle, si tu places un axe au centre du cercle et si tu tournes la structure entière de 36° (360°/10 = 36°) dans n’importe quelle direction, tu obtiendras exactement la même image qu’avant la rotation. Nous appelons cela une symétrie de rotation d’ordre 10. Étant donné que les symétries de rotation d’ordre 10 ou 5 ne se produisent pas dans les cristaux périodiques (tu peux en apprendre davantage en suivant ce lien), ce cristal ne l’était clairement pas. C’est pourquoi j’ai écrit « ordre 10 ??? » dans mon carnet, comme abréviation de « symétrie de rotation d’ordre 10 ». J’ai ajouté les trois points d’interrogation parce que je savais qu’un cristal avec une symétrie de rotation d’ordre 10 n’avait jamais été observé auparavant.
En résumé, j’avais découvert un cristal qui contredisait la définition classique et était considéré comme impossible d’après les lois de la physique de l’époque. Il y avait deux interprétations possibles de cette découverte : soit il y avait une autre explication au phénomène que j’avais observé, explication qui ne contredisait pas les définitions existantes, soit les définitions existantes devaient être mises à jour pour inclure le cristal que j’avais découvert. Dans la suite de l’article, je t’explique comment la communauté scientifique a été convaincue qu’une nouvelle définition d’un cristal était nécessaire.
La découverte des quasi-cristaux a été critiquée avant d’être acceptée
Deux ans après la découverte, j’ai publié deux articles sur le sujet avec mes collègues [1, 2]. Des milliers de chercheurs du monde entier se sont joints à nous et ont commencé à étudier les quasi-cristaux (il y a maintenant plus de 10 000 articles publiés à ce sujet). Mais une forte opposition est également apparue, dirigée par le grand scientifique américain Linus Pauling, qui avait remporté deux fois le prix Nobel. Il m’a attaqué personnellement et a même dit : « Il n’y a pas de quasi-cristaux, il y a des quasi-scientifiques ». Linus Pauling et ses partisans ont affirmé que ce que j’avais vu au microscope était dû à des cristaux jumeaux (Figure 4). Il s’agit d’un phénomène qui se produit quand deux cristaux sont couplés l’un à l’autre. Chacun des deux cristaux est ordonné et périodique, et en raison des couplages entre les figures de diffraction, le cristal semble avoir une symétrie d’ordre 5.

- Figure 4 - Cristaux jumeaux présentant une symétrie d’ordre 5.
- (À gauche) Un cristal aluminium-fer composé de cinq couples de cristaux jumeaux. Chaque ń feuille » est un cristal ordonné et périodique, et deux cristaux jumeaux (comme ceux entourés de rouge) sont des images miroirs l’un de l’autre. (À droite) Un motif de diffraction d’un cristal jumeau. Tu peux voir que le motif obtenu est similaire à celui du quasi-cristal (Figure 1). Cette image est la somme des figures de diffraction de chaque cristal individuel. Les cercles rouges dans la figure indiquent la figure de diffraction d’un cristal parmi les dix cristaux adjacents. Tu peux voir que le motif est ordonné et périodique, ce qui correspond à la définition classique d’un cristal.
J’ai immédiatement vérifié s’il y avait des jumeaux dans mes cristaux, mais je n’en ai pas trouvé et j’étais sûr de mon résultat initial. Je savais que j’avais identifié un nouveau phénomène et découvert un nouveau matériau. L’opposition de Linus Pauling à mes découvertes a duré 10 ans ! Après sa mort en 1994, l’opposition à ma découverte scientifique a presque entièrement disparu et la voie vers son acceptation complète s’est ouverte. Sa reconnaissance a entraîné une nouvelle définition de ce qu’est un cristal, et a également jeté un nouvel éclairage sur la cristallographie. Parmi les centaines de quasi-cristaux identifiés après ma découverte, certains présentent des propriétés intéressantes, telles que la résistance à la détérioration et des propriétés électriques qui varient en fonction de la température. Quelques produits utilisant des quasi-cristaux ont été fabriqués, tels que le revêtement antiadhésif pour poêles de Sitram et l’acier inoxydable renforcé de Sandvik.
Recommandations pour les jeunes scientifiques
Si tu veux devenir scientifique, tu dois développer deux qualités. Tout d’abord, tu dois intégrer le vaste monde de la science. Tu auras besoin d’une connaissance approfondie de différents domaines, tels que les mathématiques, la physique, la chimie, la biologie et l’informatique. Tu devras également savoir ce qui a déjà été découvert et ce qui est admissible ou non selon les théories actuelles. Dans le cas de ma découverte, je savais que la symétrie d’ordre 5 était impossible selon la définition alors acceptée des cristaux et n’avait jusqu’alors été observée que dans le cas de cristaux jumeaux.
Cependant, connaître les théories existantes ne suffira pas à faire de toi un scientifique accompli. Tu devras également développer une expertise spécifique. Trouve quelque chose que tu aimes faire, quelque chose dans lequel tu es doué et qui t’intéresse, et deviens un expert en la matière. J’avais développé une expertise particulière avec le MET et, à l’époque, rares étaient les personnes qui savaient l’utiliser aussi bien que moi. C’était mon avantage et c’est ce qui m’a permis de rester confiant dans mes résultats, même face aux critiques sévères de Linus Pauling.
En conclusion, rappelle-toi que la vie présente de nombreuses opportunités et que tu dois apprendre à les saisir. Rappelle-toi également que la vie est faite de beaucoup d’autres choses. Quand on me demande quels sont les moments les plus heureux de ma vie, je réponds que ce sont les naissances de mes quatre enfants et de mes 12 petits-enfants. J’espère que tu auras aussi l’occasion de t’émerveiller devant le fait de donner la vie et de comprendre le monde, et je te souhaite bonne chance pour ce parcours.
Réponse à l’énigme posée dans « qu’est-ce qu’un cristal ? »
Dans le cristal que j’ai trouvé, le rapport entre les diamètres des cercles concentriques (Figure 3, à droite) est le nombre d’or – un nombre irrationnel ayant une valeur d’environ 1,618. Ce même nombre d’or se retrouve dans le visage de la Joconde, le tableau le plus célèbre de Léonard de Vinci. Le nombre d’or donne au spectateur une impression de beauté. Vois-tu la beauté dans le motif de diffraction que j’ai découvert ?
Contributions à la version française
TRADUCTEUR : Frédéric Lemoigno (ICGM Université de Montpellier, Montpellier, France)
ÉDITEUR : Sylvie Boussès-Hurtrez et Catherine Braun-Breton (Association Jeunes Francophones et la Science, Montpellier, France)
Glossaire
Microscope électronique à transmission (TEM): ↑ Microscope qui utilise un faisceau d’électrons pour pénétrer le matériau étudié. Les électrons produisent une figure de diffraction qui montre la structure atomique du matériau.
Alliage: ↑ Matériau composé d’au moins deux éléments, dont un ou plusieurs sont des métaux.
Phase (cristal): ↑ État particulier d’un matériau. Souvent, nous parlons de phases dans le contexte de l’état du matériau (gaz, liquide, solide ou plasma), mais ici nous entendons une disposition spécifique dans l’espace des atomes le constituant.
Cristal: ↑ Matériau solide dont les éléments constitutifs (atomes, ions ou molécules) sont disposés dans l’espace de manière ordonnée.
Diffraction: ↑ Phénomène dans lequel la lumière ou les électrons sont dispersés lorsqu’ils interagissent avec un obstacle, tel qu’un cristal ou un autre matériau solide.
Quasi-cristaux: ↑ Cristaux dont les éléments constitutifs sont disposés dans l’espace de manière non périodique, ce qui signifie qu’ils ne sont pas dupliqués dans toutes les directions selon un motif répétitif.
Cristallographie: ↑ Domaine scientifique qui étudie l’arrangement spatial des atomes dans les solides, dont font partie les cristaux.
Périodicité: ↑ Propriété d’un motif répétitif qui est dupliqué à l’infini (dans le temps ou dans l’espace).
Symétrie de rotation: ↑ Propriété d’un motif se répétant par des rotations autour d’un axe central.
Ordre: ↑ Motif organisé qui n’est pas aléatoire.
Conflit d’intérêts
Les auteurs déclarent que les travaux de recherche ont été menés en l’absence de toute relation commerciale ou financière pouvant être interprétée comme un potentiel conflit d’intérêts.
Références
[1] ↑ Shechtman, D., and Blech, I. A. 1985. The microstructure of rapidly solidified Al6Mn. Metall. Trans. A 16:1005–12. doi: 10.1007/BF02811670
[2] ↑ Shechtman, D., Blech, I., Gratias, D., and Cahn, J. W. 1984. Metallic phase with long-range orientational order and no translational symmetry. Phys. Rev. Lett. 53:1951–4. doi: 10.1103/PhysRevLett.53.1951
