תַקצִיר
מדע החומרים חוקר את המבנה של חומרים שונים בטבע ואת תכונותיהם. אחד מסוגי החומרים האלה הוא הגביש (שמכונה גם 'קריסטל'). גביש הוא חומר מוצק שאבני הבניין שלו (אטומים, יונים, מולקולות) מאורגנות במרחב באופן מסודר. מלח, קוורץ ויהלום הם דוגמאות לגבישים. בגבישים רגילים, אבני הבניין האלה מאורגנות באופן מחזורי, כלומר בתבנית שחוזרת על עצמה בכל הכיוונים. לעומתם, בגבישים מיוחדים שנקראים 'קוואזי גבישים' אבני הבניין מסודרות במרחב באופן שאינו חוזר על עצמו. תגליתם של הקוואזי גבישים יצרה מהפכה במדע הקריסטלוגרפיה, ושינתה את ההגדרה הבסיסית ביותר של מהו גביש. מאז התגלית של הקוואזי גביש הראשון התגלו מאות קוואזי גבישים נוספים, חלקם בעלי תכונות פיזיקליות מיוחדות שהוטמעו ביישומים שונים.
פרופסור שכטמן זכה בפרס נובל לכימיה לשנת 2011 על גילוי הקוואזי גבישים
כיצד נעשיתי מדען של חומרים?
כשהייתי בן שבע סבא שלי הביא לי מתנה מיוחדת במינה – זכוכית מגדלת. זה שימח אותי מאוד והתחלתי להסתובב עם זכוכית המגדלת שלי בשדות של רמת גן. הסתכלתי על כל מה שמצאתי: פרחים, אבקנים, חרקים וחול ודברים נוספים שמצאתי בדרך. כך התאהבתי בעולם הדברים הקטנים. כמה שנים מאוחר יותר, כשהייתי בכיתה ה' המורה אמר שיש מיקרוסקופ בבית הספר. שבוע אחרי שבוע ביקשתי מהמורה להביא את המיקרוסקופ לכיתה. בסופו של דבר הוא הביא אותו והזמין אותי להיות הראשון שיסתכל דרכו. הוא שׂם עלה מתחת למיקרוסקופ, ואני יכולתי לראות את התנועה של הכלורופיל, מולקולה קטנה בעלה שמקנה לו את צבעו הירוק. מאותו הרגע לא יכולתי לעזוב את המיקרוסקופ. שנים אחר כך, במהלך לימודיי בטכניון, הגיע לפקולטה שלנו מיקרוסקופ חזק במיוחד שנקרא מיקרוסקופ אלקטרונים חודר (TEM, קיצור של Transmission Electron Microscope). התאהבתי במיקרוסקופ הזה כי הוא אִפְשֵׁר לי לְמַמֵּשׁ את סקרנותי המדעית לעולם הדברים הקטנים. משׁם והלאה התמחיתי בהפעלת מיקרוסקופ האלקטרונים הזה, ובאמצעותו גיליתי סוג חדש של חומרים שזיכה אותי, כמה עשרות שנים מאוחר יותר, בפרס נוֹבֶּל.
גילוי הקוואזי גבישים
בסוף שנת 1981 טסתי לשבתון בארצות הברית במטרה לחקור חומרים מבוססי-אלומיניום עבור יישומים בתחום התעופה. עבדתי על סגסוגת מתכתית של אלומיניום-ברזל וגיליתי פאזה חדשה, סידור מיוחד של האטומים בסגסוגת הזו. רציתי לחקור את הסידור הזה, אך הוא לא היה יציב והשתנה בקלות. לכן, הכנתי סגסוגות שונות של אלומיניום-מַנְגָּן, שהיו יציבות יותר. הכנתי סגסוגות של אלומיניום-מנגן בריכוזים שונים, חלקן שימושיות ליישומים בתעופה וחלקן לא, אבל הכנתי אותן מתוך סקרנות מחקרית. את כל הסגסוגות חקרתי באמצעות המכשיר הנסיוני שבו התמחיתי, ה-TEM. אני קורא לו 'מלך המיקרוסקופים' מאחר שהוא מכשיר רב עוצמה, שהאפשרויות הגלומות בו הן אדירות אם יודעים איך להפעילו בצורה מקצועית. המיקרוסקופ הזה מאפשר לראות את המבנה היסודי - במקרה שלנו את הסידור האטומי - של חומרים שונים.
ביום חמישי, 8 באפריל 1982, סרקתי באמצעות ה-TEM את הסגסוגת שהכנתי באותו היום וקיבלתי תמונה (תבנית) מיוחדת מאוד על המסך. לתבנית שנוצרת מאינטראקציה בין אלקטרונים למכשול מוצק כגון גביש, אנו קוראים תבנית דִּיפְרַקְצְיָה (ראו איור 1 משמאל). מייד זיהיתי שיש משהו מיוחד בתבנית הדיפרקציה, ושלא מדובר בגביש שגרתי, שאנו קוראים לו היום קוואזי גביש, ולכן כתבתי לעצמי הערה בסוגריים במחברת המעבדה שלי, שניסחתי באופן הבא: ''10 Fold???'' (איור 1 מימין, שורה 6). כעת אסביר לכם מה כל כך מיוחד בתבנית הזו, מה פירוש ההערה שכתבתי במחברת ומדוע היא בישרה מהפכה בעולם הקריסטלוֹגרפיה.

- איור 1 - תגליתו של הגביש הקוואזי הראשון.
- משמאל: תמונת הדיפרקציה של הקוואזי גביש אלומיניום-מַנְגָּן שגיליתי בשנת 1982. תבנית הפיזור של הנקודות בתמונה מלמדת על הסידור המרחבי של האטומים המרכיבים את החומר. מימין: מחברת המעבדה שלי שבה מתועדת הפתעתי מהתגלית (צילום 1725, שורה 6). קרדיט: דן שכטמן.
גביש – לפני התגלית ואחריה
מדע הקריסטלוגרפיה (חֵקֶר הגבישים) החל בשנת 1912 על ידי פיזיקאי גרמני בשם מקס פון לאואה. פון לאואה היה הראשון שהקרין קרני רנטגן על חומר מוצק גבישי, והוא ראה תבנית דיפרקציה מסודרת של נקודות שנבעה מהסידור המחזורי של האטומים המרכיבים את הגביש. באותה שנה, שני פיזיקאים אנגלים - האב והבן לבית בראג - ניסחו משוואה מתמטית שמתארת את התופעה הניסיונית שקיבל פון לאואה. אז נולדה הקריסטלוגרפיה כתחום מדעי חדש. במשך עשרות שנים מאז הולדת הקריסטלוגרפיה נחקרו מאות אלפי גבישים שונים, ולכולם היו שתי תכונות משותפות: הם היו מסודרים, והם היו מחזוריים (איור 2). בעקבות התצפיות האלה נוצרה ההגדרה הקלאסית של הגביש שעל פיה: ''גביש הוא חומר מוצק שבו האטומים המרכיבים אותו מסודרים במבנה קבוע החוזר על עצמו במרחב''. דוגמאות ידועות לגבישים הן גרגירי מלח, אבן קוורץ ויהלומים, אולם גם מרבית המתכות הן גבישים, למשל נחושת, ברזל, אלומיניום ועוד. תכונה נוספת שנמצאה בגבישים הקלאסיים נקראת סימטריה סיבובית, שבּה הצורה נשמרת בסיבוב סביב נקודה קבועה (איור 2, באמצע ומימין). בגלל חוקים מתמטיים של הסידור הפנימי של גבישים, מצאו שגבישים יכולים לקיים סימטריה סיבובית מסוגים שונים שנקראים 'סֵדֶר' (למשל סדר 1, 2, 3, 4 או 6; ראו איור 2 באמצע להמחשת סימטריה סיבובית מסדר 4) ולא מסוגים אחרים (למשל 5 או 10).
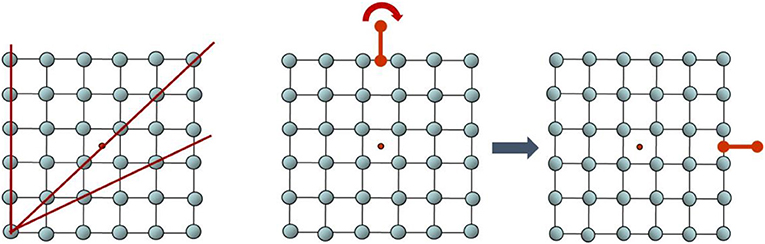
- איור 2 - סדר, מחזוריות וסימטריה סיבובית.
- משמאל: דוגמה למבנה של גביש מסודר ומחזורי פשוט (ריבועי). הגביש מסודר, כלומר הנקודות, שמייצגות אטומים המרכיבים את הגביש, מפוזרות בצורה מאורגנת שאין בה אקראיות. הגביש הוא גם מחזורי. אם תבחרו את אחד הכיוונים (המסומנים בקווים אדומים) ותתקדמו מנקודה לנקודה, תבחינו שהמרחק בין כל שתי נקודות על הקו הוא זהה. דרך אחרת לראות את המחזוריות היא שאם תבחרו כל אחד מהריבועים שמכילים ארבעה אטומים ותשכפלו אותם לכל הכיוונים, תקבלו בדיוק את המבנה המוצג בתמונה. אמצע: מבנה בעל סימטריה סיבובית מסדר 4. דמיינו שאתם אוחזים את הידית האדומה וסובבו את כל המבנה ב-90° (עם כיוון השעון). כעת הידית האדומה פונה ימינה. מימין: ללא הידית האדומה, המבנה כולו לאחר הסיבוב היה נראה לכם בדיוק כמו לפני הסיבוב. בגביש הזה המבנה חוזר על עצמו בכל סיבוב של 90°. זה נקרא סימטריה מרובעת, כי כעבור ארבעה סיבובים כאלה משלימים סיבוב שלם של 360°, וכל הנקודות חוזרות למיקומן המקורי. קרדיט: דן שכטמן.
70 שנים אחרי הולדת הקריסטלוגרפיה מצאתי גביש שהוא כן מסודר אבל הוא לא מחזורי. כדי להבין טוב יותר מה זה אומר, הסתכלו על איור 3 משמאל. אתם יכולים לראות שסביב לנקודה הגדולה במרכז התמונה מופיעים 'מעגלים' הולכים ומתרחבים (שלושת המעגלים הראשונים מסומנים בכחול, צהוב ואדום). כל אחד מהמעגלים מורכב מעשר נקודות הדומות לפרח עם חמישה זוגות של עלים מנוגדים (נקודה 1 היא הזוג של נקודה 6, נקודה 2 היא הזוג של נקודה 7, וכולֵי). אם תמדדו את המרחק מהמרכז למעגלים ההולכים ומתרחבים, תראו שהמרחק בין המרכז למעגל הראשון אינו חצי מהמרחק בין המרכז למעגל השני (קווים כחול וצהוב באיור 3 מימין). כמו כן, המרחק בין המרכז למעגל הראשון אינו שליש מהמרחק בין המרכז למעגל השלישי (קווים כחול ואדום באיור 3 מימין). כלומר, אי אפשר לקחת מעגל אחד ופשוט לשכפל אותו במרחקים שווים מהמרכז ולקבל את הגביש שקיבלתי. זה אומר לנו שהגביש הזה אינו מחזורי. מצד אחר אנו יודעים לתאר מתמטית את המרחקים בין המרכז לבין המעגלים המתרחבים, מה שאומר שהגביש כן מסודר. (חידה קצרה לסקרנים שביניכם: האם תוכלו למצוא מה הקשר בין הגביש שגיליתי לבין הציור הידוע - המונה ליזה? התשובה בסוף המאמר).
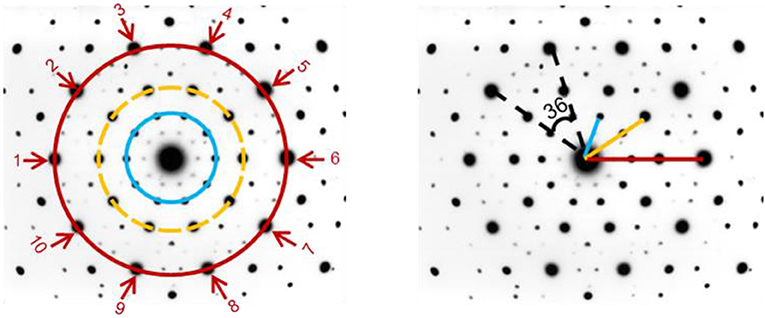
- איור 3 - תבנית הדיפרקציה של קוואזי גביש.
- משמאל: תבנית הדיפרקציה בנויה ממעגלים הולכים ומתרחבים (כחול, צהוב ואדום) שכל אחד מהם מורכב מעשר נקודות שמסודרות בזוגות (נקודה 1 היא זוג של נקודה 6, נקודה 2 היא זוג של נקודה 7, וכך הלאה). מימין: הזווית בין כל שתי נקודות על אותו המעגל היא של 36° (קו שחור מקווקו), כלומר סיבוב אחד של 36° מהמרכז מחזיר את התבנית להיראות כמו לפני הסיבוב. עשרה סיבובים כאלה יחזירו את הנקודות כולן למיקומן המקורי, ולכן התבנית הזו מוגדרת כבעלת סימטריה סיבובית מסדר 10. כמו כן אפשר לראות שהמרחק מהמרכז למעגל הראשון (קו כחול) אינו חצי מהמרחק מהמרכז למעגל השני (קו צהוב), ואינו שליש מהמרחק מהמרכז למעגל השלישי (קו אדום). זה אומר שאי אפשר לשכפל את המעגל הפנימי בכפולות שלמות מהמרכז ולקבל את התבנית הזו; משמע, התבנית אינה מחזורית.
שימו לב שהנקודות שמרכיבות כל מעגל בתמונת הדיפרקציה בתמונה 3 משמאל מסודרות במרחקים שווים זו מזו על גבי המעגל. מאחר שיש עשר נקודות הממוקמות בתזוזות קבועות זו מזו ביחס למרכז המעגל, אם תמקמו ציר במרכז המעגל ותסובבו אותו ב-36 מעלות (360°/10 = 36°) עם כיוון השעון או נגדו, תקבלו שוב בדיוק את אותה התמונה כמו קודם (איור 3 מימין) .לזה אנו קוראים סימטריה סיבובית מסדר 10. כיוון שסימטריה סיבובית של 10 או של 5 לא יכולה להתקבל בגביש מחזורי (להעמקה בנושא קראו בקישור הזה), ברור שהגביש הזה אינו מחזורי. לכן כתבתי לעצמי את ההערה ''10-Fold???'' שהיא קיצור לסימטריה סיבובית מסדר 10, והוספתי את שלושת סימני השאלה כיוון שידעתי שעד אז לא היה ידוע על גביש שיכול לקיים את הסימטריה הזו.
לסיכום, מצאתי גביש שסותר את ההגדרה הקלאסית של גביש ונחשב ''אסור'' על פי חוקי הפיזיקה של אותה התקופה. במצב זה היו שתי אפשרויות: או שיש הסבר אחר לתופעה שמצאתי, שאינו סותר את ההגדרות הקיימות, או שצריך לעדכן את ההגדרות הקיימות כך שיכללו את הגביש שגיליתי. בחלק הבא אתאר כיצד הקהילה המדעית השתכנעה שנדרש שינוי בהגדרה הבסיסית ביותר של הגביש.
התגלית של קוואזי גבישים ספגה ביקורת לפני שהתקבלה
שנתיים לאחר התגלית, בשנת 1984, פרסמתי שני מאמרים בנושא עם קולגות שלי [2 ,1]. הצטרפו אלינו אלפי חוקרים מכל העולם שהתחילו לחקור קוואזי גבישים (עד היום יש יותר מ-10,000 מאמרים בנושא). אולם מצד אחר קמה קבוצת התנגדות חזקה, שבראשה עמד המדען האמריקאי הדגול לינוס פאולינג, אשר זכה בפרס נובל פעמיים. פאולינג תקף אותי אישית ואף אמר בִּגְנוּתִי ''There are no quasi crystals, there are quasi scientists'' (''אין קוואזי גבישים, יש קוואזי מדענים''). טענותיו של פאולינג ותומכיו היו שמה שראיתי במיקרוסקופ הוא תופעה שנקראת 'תאומים' (איור 4). זו תופעה שבה שני גבישים קלאסיים צמודים זה לזה. כל אחד מהגבישים מסודר ומחזורי, אולם בגלל הצימוּד נראה שיש לגביש סימטריה מסדר 5.

- איור 4 - גבישים תאומים שמייצרים סימטריה מחומשת.
- משמאל: גביש אלומיניום-ברזל במבנה של חמישה זוגות תאומים. כל 'עלה' במבנה הוא גביש מסודר ומחזורי, וכל שני גבישים צמודים (כמו הזוג שמסומן באדום) מכונים תאומים, ומהווים תמונת ראי אחד של השני. מימין: תבנית הדיפרקציה של גביש התאומים. אפשר לראות שהתבנית שמתקבלת דומה לתבנית של הקוואזי גביש שבאיור 1. התמונה הזו מתקבלת כסכום של תמונות הדיפרקציה של כל אחד מהגבישים הבודדים. הנקודות האדומות שבתמונה מדגישות את תמונת הדיפרקציה של גביש אחד בלבד מתוך העשרה שבתמונה מימין. אפשר לראות שהתבנית היא מסודרת ומחזורית, ולכן עונה על ההגדרה הקלאסית של גביש.
מיד בדקתי אם יש תאומים בגביש שלי, אך לא מצאתי, ולכן הייתי בטוח בתגלית המקורית שלי. ידעתי שזיהיתי תופעה חדשה וגיליתי חומר לא מוכר. התנגדותו של פאולינג נמשכה עשר שנים! עם מותו של פאולינג בשנת 1994 התפוגגה גם מרבית ההתנגדות המדעית לתגלית שלי, ואז נפתחה הדלת לקבלה מלאה של התגלית. ההכרה בתגלית הובילה להגדרה חדשה של גביש, והיא גם האירה את מדע הקריסטלוגרפיה באור חדש. מִבֵּין מאות הקוואזי גבישים שהתגלו אחרי התגלית שלי, לחלקם יש תכונות שימושיות כמו התנגדות לבְּלַאי והשתנות מעניינת של התכונות החשמליות כתלות בטמפרטורה. כבר יוצרו כמה מוצרים שמשתמשים בקוואזי גבישים לשיפור תכונות המוצר, למשל ציפוי נוגד הידבקות למחבתות של החברה הצרפתית Sitram וחיזוק של פלדת אל-חלד של החברה השוודית Sandvik.
המלצות למדענים צעירים
אם את או אתה רוצים להיות מדענים אתם צריכים לפתח שתי תכונות: ראשית, אתם צריכים להכיר היטב את העולם המדעי – אתם צריכים להיות אנשי העולם הגדול במדע. כלומר, להיות בעלי ידע רחב בכמה תחומים כמו מתמטיקה, פיזיקה, כימיה, ביולוגיה ומחשבים. אתם גם צריכים לדעת מה כבר מצאו ומה עוד לא, מה ''מותר'' ומה ''אסור'' לפי התיאוריות השולטות במדע. במקרה של התגלית שלי, הייתי צריך לדעת שסימטריה מחומשת אסורה על פי ההגדרה המקובלת של גבישים, ושעד אז צפו בה רק בגבישים תאומים.
אבל, הכרת התיאוריות הקיימות אינה מספיקה כדי להיות מדענים מצליחים. נוסף על כך אתם צריכים לפתח מומחיוּת – תמצאו משהו שאתם נהנים לעשות, משהו שמתאים לכם ומעניין אתכם – ותתמחו בו. אני התמחיתי ב-TEM, ובזמנו לא היו הרבה אנשים שידעו להשתמש בתכונותיו טוב כמוני. זה היה היתרון שלי ומה שאִפְשֵׁר לי להיות בטוח בממצאים שלי ולעמוד בנחישות מול הביקורת הנוקבת של מתנגדיי, בראשות פאולינג.
לסיום, זיכרו שבמובנים רבים חיינו מציגים בפנינו הזדמנויות שונות, והחוכמה היא לדעת לנצל אותן. זיכרו גם שהחיים מורכבים מהרבה מרכיבים. ובאמת, כששואלים אותי מהם הרגעים הכי שמחים בחיי, אני אומר שאלה הם רגעי הלידה של ארבעת הילדים ושניים עשר הנכדים שלי ושל אשתי. אני מקווה שגם אתם תחוו את הפליאה שביצירת חיים ובהבנת העולם, ואני מאחל לכם הצלחה רבה בדרככם.
תשובה לחידה מהחלק ''מהו גביש'':
בגביש שמצאתי היחסים בין קטרי המעגלים המתרחבים (איור 3 משמאל) מבטאים את יחס הזהב – מספר לא רציונלי, שערכו שווה בקירוב ל-1.618. את אותו יחס הזהב, המכונה לעיתים גם חתך הזהב, אפשר למצוא בְּפָנֶיהָ של המונה ליזה – ציורו המפורסם ביותר של ליאונרדו דה וינצ'י. יחס הזהב מייצר תחושה אסתטית עבור המתבונן. האם אתם רואים את האסתטיקה בתבנית הדיפרקציה שמצאתי?
מילון מונחים
מיקרוסקופ אלקטרונים חודר (Transmission Electron Microscope, TEM): ↑ מיקרוסקופ שמשתמש בקרן של אלקטרונים לחדור דרך החומר הנבדק. האלקטרונים יוצרים תבנית דיפרקציה שמראה את המבנה האטומי של החומר.
סגסוגת מתכתית (Alloy): ↑ חומר שמורכב משני יסודות לפחות, כאשר לפחות אחד היסודות האלה הוא מתכת.
פאזה (Phase): ↑ מצב מסוים של חומר. פעמים רבות מדברים על פאזה בהקשר למצב הצבירה של החומר (גז, נוזל, מוצק או פלזמה), אולם כאן הכוונה לסידור מרחבי מסוים של האטומים שמהם מורכב החומר.
גביש (Crystal): ↑ חומר מוצק שמרכיבי היסוד שלו (אטומים, יונים או מולקולות) מסודרים במרחב בצורה מאורגנת.
דיפרקציה (Diffraction): ↑ תופעה שבה אור או אלקטרונים מתפזרים כתוצאה מאינטראקציה עם מכשול, כמו למשל גביש או חומר מוצק אחר.
קוואזי גבישים (Quasi-Crystals): ↑ גבישים שאבני הבניין שלהם מסודרות במרחב בצורה שאינה מחזורית, כלומר אינן חוזרות על עצמן בתבנית קבועה בכל הכיוונים.
קריסטלוגרפיה (Crystallography): ↑ תחום מדעי העוסק בחֵקֶר הסידור המרחבי של אטומים במוצקים ובהם גם בגבישים.
סדר (Order): ↑ תבנית מאורגנת שאינה אקראית.
מחזוריות (Periodicity): ↑ תבנית שחוזרת על עצמה שוב ושוב (בזמן או במרחב).
סימטריה סיבובית (Rotational Symmetry): ↑ תבנית חוזרת על עצמה בסיבוב סביב ציר מרכזי.
הצהרת ניגוד אינטרסים
המחבר מצהיר כי המחקר נערך בהעדר כל קשר מסחרי או פיננסי שיכול להתפרש כניגוד אינטרסים פוטנציאלי.
תודות
אני רוצה להודות לנועה שגב על עריכת הריאיון שהיווה בסיס למאמר זה, ועל כתיבה משותפת של המאמר.
מקורות
[1] ↑ Shechtman, D., and Blech, I. A. 1985. The microstructure of rapidly solidified Al6Mn. Metall. Trans. A 16:1005–12. doi: 10.1007/BF02811670
[2] ↑ Shechtman, D., Blech, I., Gratias, D., and Cahn, J. W. 1984. Metallic phase with long-range orientational order and no translational symmetry. Phys. Rev. Lett. 53:1951–4. doi: 10.1103/PhysRevLett.53.1951
