Abstract
Leo Durocher, a famous baseball player from the 1930s, once said that “Nice guys finish last.” That may be true in baseball, but it is not true in life more generally. In this article, we use ideas from the branch of mathematics known as “game theory” to study a situation known as the “Prisoners’ Dilemma (PD),” which sheds light on why people often fail to work well together. Game theory shows that people who are kind and trustworthy have a strategic advantage, as they can “change the game” to escape the PD and make everyone better off, including themselves. So, truly, “nice guys finish first.”
Introduction: Games, Games Everywhere
No man is an island, entire of itself. (John Donne, seventeenth-century English poet)
When people speak of “games,” they are usually talking about amusements, like checkers and Monopoly, or sports, like football or basketball. But in the branch of mathematics known as “game theory,” we speak of games in a much broader sense.
Definition: Game
A situation is a “game” whenever (i) more than one person is making a decision and (ii) people’s decisions impact one another.
Just about everything we do in life is a game in the game-theory sense. At home, at school, everywhere we go, and just about everything we do, we are playing games. Do not believe me? Think back to the very beginning of your day, when you woke up. How quickly you got out of bed impacted your parents—and how early they woke you up impacted you—so that was a game! Think about what happened next, throughout the rest of the day. From the bathroom to the breakfast table, in the classroom and on the playground, you make choices that impact others as well as yourself. You’re playing games! Knowing about game theory can help you improve your experience in those situations—not just to “win,” but to improve your relationships and have a happier life.
Game theory is used to study how people are likely to behave in strategic situations, with applications in economics, political science, business strategy, law, entrepreneurship, and military science, to name just a few. Just as physics describes how planets revolve around the sun, game theory seeks to describe how people make decisions in games. Mathematics is useful in game theory as a tool to analyze players’ motivations and to predict outcomes. Sometimes, as in the next example, the predictions that game theory makes can be quite unexpected.
Example: Eating Out with Friends
Eight friends have decided to go out together for lunch at a burger restaurant. They will split the bill equally. There are two items on the menu: (i) a regular burger that costs $4 and (ii) a deluxe burger that costs $8. Each friend feels that eating a regular burger is worth $5 while eating a deluxe burger is worth $6. Note that a regular burger is worth more than it costs ($5 > $4) while a deluxe burger is worth less than it costs ($6 < $8). Deluxe burgers are obviously a bad deal—you have to pay $8 for something that is only worth $6 to you—but game theory predicts that, when eating together, all eight friends will splurge on deluxe burgers. Why?
To understand this unexpected outcome, it is helpful to think about the game from a mathematical point of view. Let D be the number of friends who order deluxe and let R be the number who order regular. (D and R are integers from 0 to 8, with R + D = 8, because there are eight friends in total.) Since deluxe burgers cost $8 and regular ones cost $4, the total bill is 8D + 4R. Since R = 8 − D, we can rewrite this as 8D + 4 (8 − D). Multiplying this out, we get 8D + 32 − 4D which can be simplified to
Each friend’s individual bill is 1/8th of the total bill. Since the total bill is 32 + 4D, each friend pays 32/8 + 4D/8 which can be simplified to
When someone upgrades their order from “regular” to “deluxe,” they get an extra dollar of value from the burger (it’s now worth $6 to them instead of $5). However, they only pay an extra 50 cents, since the additional $4 cost for the deluxe burger is split eight ways. Each individual, therefore, has a motivation to order a deluxe burger even though, when everyone does this, they all wind up paying $8 for something that is only worth $6 to them. (What would happen if one person in the group decided to order a regular burger? The total bill would fall from $64 to $60, causing everyone’s individual bill to fall from $8 to $7.50. So, the person who ordered the regular burger would have to pay $7.50 for something that is only worth $5 to them, even worse than paying $8 for something that is only worth $6.)
This seems strange but, in fact, this turns out to be an example of the most famous and most well-studied strategic situation in game theory—the game known as the “Prisoners’ Dilemma (PD).”
The Prisoners’ Dilemma
Princeton mathematician and early game theorist1 Albert Tucker came up with the story of the PD in 1950, to demonstrate an unexpected lesson of game theory—that sometimes doing what is best for ourselves individually can make everyone worse off.
Story of the PD
The police have arrested two criminals—“Prisoner #1 (P1)” and “Prisoner #2 (P2)”—on charges that carry a prison term of up to 5 years. But the police strongly suspect that the criminals also committed a worse crime, armed robbery, which carries a prison term of up to 20 years. The police interrogator places the prisoners in separate cells and tells each prisoner, “It’s time for you to confess to the robbery. How long you stay in prison depends on who confesses. If only you confess, I will let you walk free today. Otherwise, you will spend 5 years behind bars if neither of you confesses, 10 years if both confess, or 20 years if you are the only one not to confess.” What should we expect the prisoners to do?
Figure 1 shows how long P1 will spend in jail, depending on who chooses to confess. Notice that, no matter what P2 does, P1 is better off confessing himself. (If P2 confesses, confessing allows P1 to spend 10 years rather than 20 years in jail. If P2 does not confess, confessing allows P1 to go free rather than spending 5 years in jail. Either way, P1 has an individual motivation to confess.) Of course, this logic also applies to P2. Game theory, therefore, predicts that both prisoners will confess and both spend 10 years in jail—a “lose–lose outcome” since they could have both spent only 5 years in jail if they had both stayed quiet.
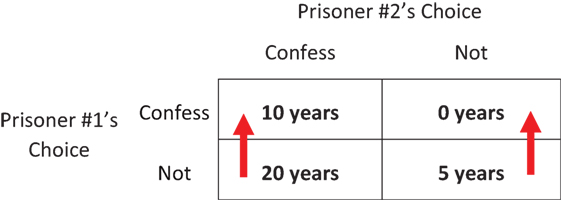
- Figure 1 - Jail time for Prisoner #1 in the Prisoners’ Dilemma.
- This “payoff matrix” shows how much time Prisoner #1 will spend in jail, depending on who confesses. There are four boxes, corresponding to the four possible outcomes of the game. (Prisoner #1’s choices are shown in the rows and Prisoner #2’s are shown in the columns.) Note that Prisoner #1 has an individual motivation to confess—illustrated by the red arrows—whether Prisoner #2 confesses or not.
The PD in Real Life
You will probably never be interrogated by the police, but many situations that we face in life are essentially the same as the PD, from a game-theory point of view. To make this point as clearly as possible, it is helpful to define what I mean by “Prisoners’ Dilemma” more precisely. That way, we can more easily identify when a real-world situation is a PD, even when no prisoners are involved. To do so, I first need to define another important game-theory concept: “dominant strategy.”
Definition: Dominant Strategy
A “dominant strategy” for a player is an action that gives that player the highest possible payoff, no matter what actions others choose.
Definition: Prisoners’ Dilemma
A game is a “Prisoners’ Dilemma” whenever (i) all players have a dominant strategy and (ii) all players are better off if they all choose not to play their dominant strategies.
This definition of the PD does not say anything about how many players are in the game. In the classic story, there are only two prisoners, but this is unimportant. The same basic game could have been played with any number of prisoners. For instance, the “Eating Out with Friends” game we considered earlier is a PD with eight players, with dominant strategy “order a deluxe burger” (rather than “confess”) and collectively bad outcome “everyone overpays for their meal” (rather than “everyone spends more time in jail”). Here, are two other examples of many-player PDs that we encounter in everyday life.
Example: Littering
Every weekend, picnickers at a local park decide whether to throw away their trash. Individually speaking, each person is better off leaving their trash on the ground—it is a hassle to throw it away—but, if everyone were to do that, the park would be a mess. In this PD played among picnickers, each player’s dominant strategy is to leave their trash on the ground, leading to a collectively bad outcome in which the park is a mess.
Example: Standing up to a Bully
There is a bully who picks on all the kids in your class. When the bully is picking on someone else, will you stand up in defense of the other kid or will you stand by and do nothing? Individually speaking, you and every other kid in class prefer not to stand up to the bully—he might start going after you instead—but, if everyone were to do that, the bully will never stop. In this PD played among kids, each player’s dominant strategy is not to stand up to the bully, leading to a collectively bad outcome in which the bully is never stopped.
Escaping the PD: The Power of Helping Others
Do unto others what you want them to do unto you. (The Golden Rule)
In the PD, everyone gets a worse outcome when they do what is best for themselves individually than if they each make a personal sacrifice to help others. One way to escape the PD is, therefore, to change players’ motivations so that they want to help others. For instance, in the littering example, a neighborhood association could put up posters urging picnickers to “Be A Good Neighbor: Throw Out Your Trash.” By emphasizing how “good neighbors” throw out their trash, such posters could cause people to start cleaning up after themselves because they want to feel like “good neighbors”—and because they want to avoid being thought of as “bad neighbors.” As long as these new feelings are strong enough to persuade everyone to clean up, everyone will be better off than before, because the park will be clean and people will feel good about themselves and their neighbors for behaving well.
Escaping the PD: The Power of Promises
You scratch my back and I’ll scratch yours. (Old saying, believed to have originated among English sailors during the seventeenth century)
Back in the seventeenth century, English sailors caught drunk on duty faced severe punishment. They were tied to the ship’s mast and beaten with a whip (known as a “cat o’ nine tails”) by another crew member. To avoid serious injury, sailors struck deals to whip each other lightly (merely “scratching” each other’s backs). So long as everyone agreed to the deal, everyone could then be sure to receive a light whipping when their time for punishment came.
“You scratch my back and I’ll scratch yours” is an example of a promise—a commitment to do something that helps another person if that other person first does something to help you. A promise can also help players escape the PD.
The Prisoner’s Promise
If you don’t confess, I promise that I also won’t confess. However, if you do confess, then so will I.
Suppose that P2 makes this promise and P1 believes it. P1’s choice is then between 10 years in jail (if both confess) or 5 years in jail (if neither confesses), and he will choose not to confess. PD solved! See Figure 2. But what if P1 does not believe P2? If P1 feels that P2 will break his promise, P1 will confess and both will go to jail for 10 years. Still locked in the dilemma!
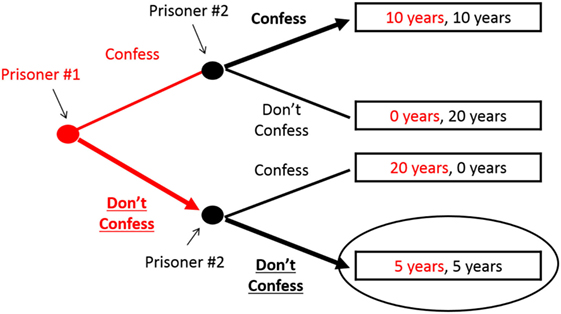
- Figure 2
- The Prisoner’s Promise allows the players to “escape” the PD. This figure shows the “game tree” of the PD when one player (Prisoner #1) moves first and the last-mover (Prisoner #2) is able to commit to the Prisoner’s Promise. Everything shown in red is for Prisoner #1, while everything in black is for Prisoner #2. The game proceeds from left to right. The choice that each player makes at each “decision node” is shown with a thick arrow, while the choice they do not make is shown with a thin line. The predicted outcome—that neither confesses and both serve 5 years in jail—is circled.
How can you make sure that others believe you when you make a promise? The simplest and most powerful approach is to be an honest and honorable person. If others know that “your word is your bond” and that you care about your personal reputation, they will trust you to do what you say. You can then fully use the power of promises, to escape the PD in your own life and to make yourself and everyone around you better off.
Suggested Further Reading
This article discusses two ways to escape the PD—by either changing what motivates players or by committing to a promise. However, there are in fact five different “escape routes” from the PD. For more on this and other game-theory topics, see my book Game-Changer and the other suggested readings listed below.
Books that provide easy-to-read introductions to game theory:
“Game-Changer: Game Theory and the Art of Transforming Strategic Situations” by David McAdams, 2014
“Thinking Strategically: The Competitive Edge in Business, Politics, and Everyday Life” by Avinash K. Dixit and Barry J. Nalebuff, 1991
Books that dig into important applications of game-theory ideas:
“Getting to YES: Negotiating Agreement Without Giving In” by Roger Fisher and William Ury, 1981
“Who Gets What—And Why” by Alvin E. Roth (winner of the Nobel Prize in Economics), 2015
My favorite game-theory textbook:
“Games of Strategy, fourth edition” by Avinash Dixit, Susan Skeath, and David H. Reiley, Jr., 2015
Conflict of Interest Statement
The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Footnote
[1] ↑ One of Tucker’s PhD students, John Nash, went on to win the Nobel Prize in Economics for his contributions to game theory. The Oscar-winning movie “A Beautiful Mind” tells the story of Nash’s life during the years when he was Tucker’s student at Princeton, with Russell Crowe starring as Nash.
