ملخص
قال Leo Durocher لاعب البيسبول الشهير من ثلاثينيات القرن العشرين ذات مرة: ”إن الأشخاص اللطفاء يخسرون دائمًا“، وقد يكون هذا صحيحًا في لعبة البيسبول، لكنه ليس صحيحًا في الحياة بشكل عام. في هذا المقال، نستخدم أفكارًا من فرع الرياضيات المعروف باسم ”نظرية الألعاب“ لدراسة موقف يُطلق عليه ”معضلة السجينين (PD)“، والتي تسلط الضوء على سبب إخفاق الأشخاص في العمل معًا بشكل جيد. تظهر نظرية الألعاب أن الأشخاص اللطفاء والجديرين بالثقة لديهم ميزة استراتيجية، حيث يمكنهم ”تغيير اللعبة“ للخروج من معضلة السجينين وتحقيق المصلحة المثلى للجميع، بما في ذلك أنفسهم، لذا في الحقيقة فإن ”الأشخاص اللطفاء يفوزون“.
مقدمة: الألعاب تحيط بنا من كل مكان
لا أحد منا يمثل جزيرة منعزلة بذاتها، فجميعنا مترابطون. (John Donne، شاعر إنجليزي من القرن السابع عشر).
عندما يتحدث الناس عن "الألعاب"، فإنهم عادةً ما يتحدثون عن التسلية، مثل لعبة الشطرنج وبنك الحظ، أو الرياضة؛ مثل كرة القدم أو كرة السلة. ولكن في فرع الرياضيات المعروف باسم "نظرية الألعاب"، نتحدث عن الألعاب من منظور أوسع بكثير.
تعريف: اللعبة
يعتبر الموقف بمثابة "لعبة" عندما (1) يكون القرار في يد أكثر من شخص و(2) عندما تؤثر قرارات الأشخاص على بعضهم البعض.
لذا فإن كل ما نقوم به في الحياة هو لعبة من مفهوم نظرية الألعاب. ففي المنزل وفي المدرسة وفي كل مكان نذهب إليه وكل شيء نقوم به تقريبًا، نحن نمارس الألعاب. ألا تصدقني؟ فكر في بداية يومك عندما تستيقظ من النوم، ومدى تأثير سرعة استيقاظك على والديك - ومدى تأثير استيقاظهما مبكرًا عليك - لذا كل ذلك كان لعبة! فكر فيما حدث بعد ذلك طوال اليوم، فخلال مسارك من الحمام إلى مائدة الإفطار، وفي الصفوف الدراسية وفي الملعب، تقوم باتخاذ اختيارات تؤثر على الآخرين وعلى نفسك أيضًا. أنت تمارس الألعاب! فعند تعرفك على نظرية الألعاب، قد تساعدك هذه النظرية على تحسين تجربتك في تلك المواقف - ليس فقط "للفوز"، ولكن لتحسين علاقاتك والحصول على حياة أكثر سعادة.
تُستخدم نظرية الألعاب لدراسة السلوك المرجح للأشخاص في المواقف الاستراتيجية، بجانب تطبيقها في مجالات الاقتصاد والعلوم السياسية واستراتيجية الأعمال والقانون وريادة الأعمال والعلوم العسكرية على سبيل المثال لا الحصر. وتسعى نظرية الألعاب إلى توضيح آلية اتخاذ الأشخاص للقرارات في الألعاب تمامًا مثلما تصف الفيزياء آلية دوران الكواكب حول الشمس. وتلعب الرياضيات دورًا مهمًا في نظرية الألعاب باعتبارها أداة لتحليل دوافع اللاعبين والتنبؤ بالنتائج. وفي بعض الأحيان، كما في المثال التالي، قد تكون التنبؤات التي تطرحها نظرية الألعاب غير متوقعة تمامًا.
مثال: تناول الطعام بالخارج مع الأصدقاء
قرر ثمانية أصدقاء الخروج لتناول الغداء في مطعم برجر، وقرروا أن يتقاسموا الفاتورة بالتساوي. يوجد عنصران في قائمة المطعم: (1) برجر عادي بتكلفة 4 دولارات و(2) برجر فاخر بتكلفة 8 دولارات. يشعر كل صديق أن البرجر العادي يستحق 5 دولارات بينما البرجر الفاخر يستحق 6 دولارات. لاحظوا أن البرجر العادي يستحق أكثر من تكلفته (5 دولارات < 4 دولارات) في حين أن البرجر الفاخر يستحق أقل من تكلفته (6 دولارات > 8 دولارات). لذا فمن الواضح أن البرجر الفاخر صفقة خاسرة – إذ عليك أن تدفع 8 دولارات مقابل شيء لا يساوي إلا 6 دولارات بالنسبة لك - ولكن نظرية الألعاب تتنبأ بأنه، عند تناول الطعام معًا، سوف يحاول الأصدقاء الثمانية التباهي من خلال اختيار البرجر الفاخر. لماذا؟
لفهم هذه النتيجة غير المتوقعة، من المفيد التفكير في اللعبة من وجهة نظر رياضية. ليكن D هو عدد الأشخاص الذين يطلبون البرجر الفاخر وليكن R هو عدد الأشخاص الذين يطلبون البرجر العادي. (D وR عددان صحيحان من 0 إلى 8، مع كون R + D = 8، لأن هناك ثمانية أصدقاء في المجمل). ونظرًا لأن تكلفة البرجر الفاخر تساوي 8 دولارات في حين أن تكلفة البرجر العادي تساوي 4 دولارات، فإن إجمالي الفاتورة هو 8D + 4R. وبما أن R = 8 - D، فيمكننا إعادة كتابتها بالصيغة التالية 8D + (8 – D)4. وبضرب ذلك معًا، نحصل على 8D + 32 - 4D والتي يمكن تبسيطها إلى:

فاتورة كل شخص من الأصدقاء الثمانية تساوي ثمن (1/8) إجمالي الفاتورة، ونظرًا لأن إجمالي الفاتورة هو 32 + 4D، فإن كل شخص سيدفع 32/8 + 4D/8 والتي يمكن تبسيطها إلى:

وعندما يقوم شخص ما بترقية طلبه من "عادي" إلى "فاخر"، فإنه سيتكبد تكلفة أعلى (يصبح الآن 6 دولارات بدلًا من 5 دولارات بالنسبة له). ومع ذلك، فإنهم سيدفعون فقط 50 سنتًا إضافيًا، نظرًا لأن التكلفة الإضافية البالغة 4 دولارات للبرجر الفاخر مقسمة على ثمانية. لذلك، فإن كل شخص لديه دافع لطلب برجر فاخر، على الرغم من أنه عندما يطلب الجميع برجر فاخر، فإنهم جميعًا ينتهي بهم الأمر بدفع 8 دولارات مقابل شيء يساوي 6 دولارات فقط. (ماذا سيحدث إذا قرر شخص في المجموعة طلب برجر عادي؟ سوف ينخفض إجمالي الفاتورة من 64 دولارًا إلى 60 دولارًا، مما يتسبب في انخفاض فاتورة كل فرد من 8 دولارات إلى 7.50 دولارًا. لذا، سيضطر الشخص الذي طلب البرجر العادي إلى دفع 7.50 دولارًا مقابل شيء لا يساوي سوى 5 دولارات بالنسبة له، وهو أسوأ من دفع 8 دولارات مقابل شيء يساوي 6 دولارات فقط).
يبدو هذا غريبًا، ولكن في الواقع، يعتبر هذا مثالًا على الحالة الاستراتيجية الأكثر شهرة والأكثر دراسة في نظرية الألعاب - اللعبة المعروفة باسم "معضلة السجينين" (PD).
معضلة السجينين
ابتكر Albert Tucker، عالم الرياضيات في جامعة برنستون وأحد واضعي نظرية الألعاب الأوائل1 ، نظرية معضلة السجينين في عام 1950، لتوضيح درس غير متوقع لنظرية الألعاب - وهو أن القيام بما هو أفضل لأنفسنا بشكل فردي قد يجعل الجميع أسوأ حالًا في بعض الأحيان.
قصة معضلة السجينين
ألقت الشرطة القبض على اثنين من المجرمين - "السجين رقم 1" و "السجين رقم 2" - بتهم تصل عقوبتها إلى السجن حتى 5 أعوام، ولكن الشرطة تشتبه بقوة في أن المجرمين ارتكبا أيضًا جريمة أسوأ، وهي السطو المسلح، والتي تصل عقوبتها إلى السجن حتى 20 عامًا. يضع محقق الشرطة السجينين في زنزانتين منفصلتين ويخبر كل سجين بالتالي: "حان الوقت لكي تعترف بالسرقة. وستعتمد مدة عقوبتك على الشخص الذي سيعترف، وإذا اعترفت، فسأطلق سراحك اليوم. بخلاف ذلك، ستقضي 5 أعوام خلف القضبان إذا لم يعترف أي منكما، أو 10 أعوام إذا اعترف كلاكما، أو 20 عامًا إذا كنت أنت الوحيد الذي لم يعترف". ما توقعاتنا في هذه الحالة؟
يوضح الشكل 1 المدة التي سيقضيها السجين رقم 1 في السجن، اعتمادًا على من سيختار الاعتراف. لاحظ أنه بغض النظر عما سيفعله السجين رقم 2، من الأفضل أن يعترف السجين رقم 1 بنفسه. (إذا اعترف السجين رقم 2، فسيؤدي الاعتراف بالسجين رقم 1 إلى قضاء 10 أعوام بدلًا من 20 عامًا في السجن. وإذا لم يعترف السجين رقم 2، فإن الاعتراف سيمنح للسجين رقم 1 حريته بدلًا من قضاء 5 أعوام في السجن، وفي كلتا الحالتين، السجين رقم 1 لديه دافع فردي للاعتراف). وبالطبع هذا المنطق ينطبق أيضًا على السجين رقم 2. وبالتالي، فإن نظرية الألعاب تتنبأ بأن كلا السجينين سيعترفان وسيقضيان 10 أعوام في السجن - وهي "نتيجة خاسرة للكل" حيث كان بإمكانهما قضاء 5 أعوام فقط في السجن إذا التزما الصمت.
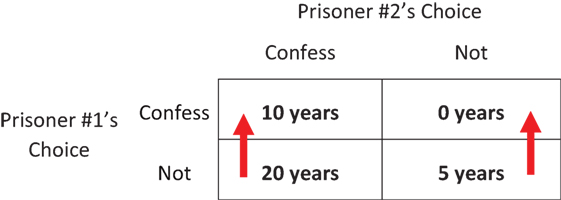
- شكل 1 - مدة السجن للسجين رقم 1 في معضلة السجينين.
- توضح "مصفوفة المردود" المدة التي سيقضيها السجين رقم 1 في السجن، اعتمادًا على من سيعترف. هناك أربعة مربعات تقابل النتائج الأربع المحتملة للعبة. (تظهر خيارات السجين رقم 1 في الصفوف وتظهر خيارات السجين رقم 2 في الأعمدة). لاحظ أن السجين رقم 1 لديه دافع فردي للاعتراف - كما يتضح من الأسهم الحمراء - سواء اعترف السجين رقم 2 أم لا.
معضلة السجينين في سياق واقعي
ربما لن يتم استجوابك أبدًا من قبل الشرطة، ولكن العديد من المواقف التي نواجهها في الحياة تشبه في الأساس معضلة السجينين، وذلك حسب نظرية الألعاب. ولتوضيح هذه النقطة بأكبر قدر ممكن، من الأفضل تحديد ما أعنيه بمصطلح "معضلة السجينين" بشكل أكثر دقة، وبهذه الطريقة، يمكننا أن نحدد بسهولة أكبر متى يكون الوضع في العالم الواقعي يشبه معضلة السجينين، حتى عندما لا يكون هناك سجينين في حقيقة الأمر. وللقيام بذلك، أحتاج أولًا إلى تحديد مفهوم آخر لنظرية الألعاب: "الاستراتيجية المهيمنة".
تعريف: الاستراتيجية المهيمنة
تتمثل "الاستراتيجية المهيمنة" لأي لاعب في الخطوة التي تمنح هذا اللاعب أعلى مردود ممكن، بغض النظر عن الإجراءات التي يختارها الآخرون.
تعريف: معضلة السجينين
تعتبر اللعبة بمثابة "معضلة سجينين" كلما كان (1) كل اللاعبين لديهم استراتيجية مهيمنة و(2) عندما تكون مصلحة جميع اللاعبين في عدم تطبيق استراتيجيتهم المهيمنة.
وهذا التعريف لمعضلة السجينين لا يحدد عدد اللاعبين في اللعبة. ففي القصة الكلاسيكية، يوجد سجينان فقط، لكن هذا غير مهم، إذ كان من الممكن لعب نفس اللعبة الأساسية مع أي عدد من السجناء. فعلى سبيل المثال، تعد لعبة "تناول الطعام بالخارج مع الأصدقاء" التي ذكرناها سابقًا بمثابة "معضلة سجينين" ولكن مع ثمانية لاعبين، وتتمثل الاستراتيجية المهيمنة في "طلب برجر فاخر" (بدلًا من "الاعتراف") وحدوث نتائج سيئة للجميع "كل لاعب يدفع أكثر من اللازم مقابل وجبته" (بدلًا من "قضاء الجميع مدة أطول في السجن"). وفيما يلي نستعرض مثالين آخرين على معضلة السجينين التي نواجهها في الحياة اليومية وتتضمن العديد من اللاعبين.
مثال: إلقاء القمامة
كل عطلة نهاية أسبوع، يقف المتنزهون في إحدى الحدائق المحلية أمام قرار التخلص من قمامتهم أم تركها على الأرض. وبصورة فردية، قد يفضل كل شخص ترك قمامته على الأرض - حيث إن التخلص منها أمر متعب - ولكن، في حال قيام الجميع بفعل ذلك، ستكون الحديقة في حالة فوضى. في لعبة معضلة السجينين هذه التي يلعبها المتنزهون، تتمثل الاستراتيجية المهيمنة لكل لاعب في ترك القمامة على الأرض، مما يؤدي بدوره إلى نتيجة سيئة على الجميع حيث ستتحول إلى الحديقة إلى حالة من الفوضى.
مثال: التصدي لشخص متنمر
هناك شخص متنمر يضايق جميع الأطفال في صفك. فالسؤال هنا عندما يضايق هذا المتنمر شخصًا آخر، هل ستتصدى له دفاعًا عن الشخص الآخر أم ستتنحى جانبًا دون فعل شيء؟ بصورة فردية، ستفضل أنت وأي شخص آخر في الصف عدم التصدي للمتنمر - بالرغم من إنه قد يطاردك أنت بدلًا من ذلك - ولكن، في حال قيام كل فرد بالانسحاب، لن يتوقف المتنمر أبدًا عن أفعاله. في لعبة معضلة السجينين هذه التي يلعبها الأطفال، تتمثل الاستراتيجية المهيمنة لكل لاعب في عدم التصدي للمتنمر، مما يؤدي بدوره إلى نتيجة سيئة على الجميع وهي عدم توقف المتنمر عن مضايقة الأشخاص الآخرين.
الخروج من معضلة السجينين: قوة مساعدة الآخرين
عامل الناس كما تحب أن تُعامل. (القاعدة الذهبية)
في معضلة السجينين، يواجه كل فرد نتيجة سيئة، عندما يقوم كل فرد بما هو أفضل له شخصيًا مقارنةً بالنتيجة التي ستحدث عندما يقوم كل فرد بتقديم تضحية شخصية لمساعدة الآخرين. لذلك، تتمثل طريقة الخروج من معضلة السجينين في تغيير دوافع اللاعبين وحثهم على مساعدة الآخرين. على سبيل المثال، في مثال إلقاء القمامة، يمكن لإحدى مؤسسات الحي وضع ملصقات تناشد المتنزهين كالتالي "كن جارًا جيدًا: تخلص من قمامتك". من خلال إلقاء الضوء على دور "الجيران الجيدين" في التخلص من قمامتهم، يمكن أن تحث هذه الملصقات الأفراد على البدء في تنظيف ما يتخلف عنهم من فضلات؛ لأنهم يرغبون في أن يكونوا "جيرانًا جيدين" - ولأنهم يودون تجنب وصفهم "بالجيران السيئين". بما أن هذه المشاعر والحوافز الجديدة التي تتولد لدى الأشخاص قوية بما فيه الكفاية لإقناع كل شخص بالتنظيف، سيكون حال كل شخص أفضل مما كان عليه مسبقًا، لأن الحديقة ستكون نظيفة وسيشعر الأفراد بالرضا عن أنفسهم وعن جيرانهم لتصرفهم الجيد.
الخروج من معضلة السجينين: قوة الوعود
قدم العون لي... أقدم العون لك. (مثل قديم يُعتقد أنه كان شائعًا بين البحارة الإنجليز خلال القرن السابع عشر)
في القرن السابع عشر، تلقى مجموعة من البحارة الإنجليز عقابًا شديدًا نتيجة القبض عليهم في حالة سكر (مخمورين) أثناء تأدية العمل، وقام عضو آخر من الطاقم بربطهم في سارية السفينة وضربهم بسوط (يُسمى "السوط متعدد الأطراف ذو التسعة ذيول"). ولتفادي حدوث إصابات خطيرة، اتفق البحارة على جلد بعضهم البعض بالسوط برفق (أي "خدش" ظهور بعضهم البعض فحسب). فبموافقة الجميع على هذا الاتفاق، يمكن أن يتأكد كل فرد بأنه سيتلقى ضربة خفيفة بالسوط عندما يأتي دوره.
يُعد مثل "قدم لي العون أقدم لك العون" مثال على الوعد - وهو الالتزام بفعل شيء من شأنه مساعدة شخص آخر، في حال قام هذا الشخص الآخر أولًا بشيء لمساعدتك.
يمكن للوعد أيضًا أن يساعد اللاعبين على الخروج من معضلة السجينين.
وعد السجين
إذا لم تعترف، أعدك بألا أعترف أيضًا. ولكن، إذا أعترفت، فسأعترف أنا أيضًا.
افترض أن السجين رقم 2 قطع هذا الوعد، وقام السجين رقم 1 بتصديقه. بالتالي، سيكون أمام السجين رقم 1 خيارين إما قضاء 10 أعوام في السجن (إذا اعترف كلا السجينين) أو 5 أعوام في السجن (إن لم يعترف كلاهما)، وسيختار السجين ألا يعترف. وبالتالي تم حل معضلة السجينين! يُرجى الاطلاع على الشكل 2. ولكن ماذا لو لم يصدق السجين رقم 1 السجين رقم 2؟ إذا شعر السجين رقم 1 أن السجين رقم 2 سينقض وعده، فسيعترف السجين رقم 1، وسيقضي كلاهما 10 أعوام في السجن، وبالتالي لن يتم حل المعضلة!
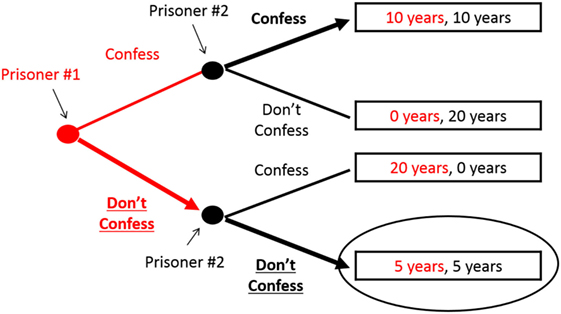
- شكل 2 - وعد السجين أتاح للاعبين "الخروج" من معضلة السجينين.
- يوضح هذا الشكل "مخطط لعبة" معضلة السجينين ويبين الحال الذي سيكون عليه الأمر بأخذ أحد اللاعبين (السجين رقم 1) زمام المبادرة من خلال تصديق الوعد والتزام اللاعب الآخر (السجين رقم 2) بتنفيذ الوعد. يشير كل شيء باللون الأحمر إلى السجين رقم 1، بينما يشير كل شيء باللون الأسود إلى السجين رقم 2. تسير اللعبة من اليسار إلى اليمين. يظهر الخيار الذي يلجأ إليه كل لاعب عند كل "نقطة قرار" في شكل سهم سميك، بينما يظهر الخيار المستبعد في شكل خط رفيع. تُحاط النتيجة المتوقعة - التي تتمثل في عدم اعتراف كلا السجينين وقضاء 5 أعوام في السجن - بدائرة.
كيف يمكنك التأكد من أن الآخرين يصدقوك عندما تقطع وعدًا؟ أبسط الطرق وأكثرها فاعلية تتمثل في أن تكون شخصًا أمينًا وشريفًا. إذا عرف الآخرون أن "وعدك هو التزامك" وأنك تخشى على سمعتك الشخصية، فسيثقون بأنك تفي بما تعد. وبالتالي، يمكنك استخدام الوعود، للخروج من معضلة السجينين في حياتك الخاصة، لتحقيق المصلحة المثلي لك ولمن حولك.
مراجع إضافية للقراءة عن هذا الموضوع
يعرض هذا المقال طريقتين للخروج من معضلة السجينين — وذلك من خلال تغيير دوافع اللاعبين أو من خلال الالتزام بوعد. ومع ذلك، يوجد في الحقيقة خمس "طرق مختلفة للخروج" من معضلة السجينين. لمعرفة المزيد حول هذا الموضوع والمواضيع الأخرى المتعلقة بنظرية الألعاب، يُرجى الرجوع إلى كتابي "قواعد اللعبة" (Game-Changer) والمراجع الإضافية الواردة أدناه.
فيما يلي نسرد كتبًا تعرض مقدمات يسهل قراءتها عن نظرية الألعاب:
“Game-Changer: Game Theory and the Art of Transforming Strategic Situations” by David McAdams, 2014
“Thinking Strategically: The Competitive Edge in Business, Politics, and Everyday Life” by Avinash K. Dixit and Barry J. Nalebuff, 1991
يرد فيما يلي الكتب التي تتعمق في التطبيقات المهمة لأفكار نظرية الألعاب:
“Getting to YES: Negotiating Agreement Without Giving In” by Roger Fisher and William Ury, 1981
“Who Gets What—And Why” by Alvin E. Roth (winner of the Nobel Prize in Economics), 2015
كتابي المفضل عن نظرية الألعاب:
“Games of Strategy, fourth edition” by Avinash Dixit, Susan Skeath, and David H. Reiley, Jr., 2015
إقرار تضارب المصالح
يعلن المؤلفون أن البحث قد أُجري في غياب أي علاقات تجارية أو مالية يمكن تفسيرها على أنها تضارب محتمل في المصالح.
هامش
[1] ↑ فاز John Nash، وهو أحد طلاب الدكتوراة لدى عالم الرياضيات Tucker، بجائزة نوبل في الاقتصاد نظير إسهاماته في نظرية الألعاب. ويحكي فيلم "عقل جميل" (A Beautiful Mind) الحائز على جائزة الأوسكار قصة حياة Nash خلال السنوات التي كان فيها طالبًا لدى Tucker في جامعة برنستون، وأدى الممثل Russell Crowe دور Nash في هذا الفيلم.
