תַקצִיר
בעלי חיים שצדים חיות אחרות כדי להזין את עצמם מכונים 'טורפים'. בעלי חיים ניצודים ידועים כ'טֶרֶף'. מה קורה, לדעתכם, כאשר טורף מגיע למערכת אקולוגית שבה הטֶּרף חי בעבר ללא חשש להיאכל? האם טורף חדש יאכַל את כל בעלי החיים הנטרפים, עד שאלו ייכחדו? למעשה, מערכת היחסים בין הטורף לטרף מעניינת הרבה יותר מכך. במאמר זה, נציג איך נראית מערכת היחסים בין הטורף לטרף לאורך זמן, ונסביר כיצד מדענים יכולים לחזות את גודל האוכלוסייה העתידי – כל זאת באמצעות פעולות מתמטיות בסיסיות כמו חיבור, חיסור וכפל.
מדוע אנו חוקרים אוכלוסיות של חיות?
מדענים נדרשים לאסוף מידע כדי שיוכלו להבין איך להגֵן על הסביבה ועל החיות המתקיימות בה. לפעמים, מדענים משתמשים במתמטיקה במטרה לבחון את התיאוריות שלהם על אודות חיות, או אפילו כדי לנסות לחזות את העתיד! אנו מכנים זאת 'מוֹדֶל מתמטי'. יצירת מודל של מערכת היחסים בין הטורפים לטרף מסייעת למדענים להבין איך האוכלוסיות הללו משתנות במשך הזמן, ומאפשרת להם לדעת כשחיה עלולה להימצא בסכנת הכחדה. כדי ליצור מודל מתמטי מוצלח, עָלֵינו לאסוף נתונים מהסביבה. במאמר זה, נראה כיצד מתמטיקה בסיסית כמו חיבור, חיסור וכפל, יכולה לשמֵּש ליצירת מודל של מערכות היחסים הנצפות בטבע בין הטורף לטרף.
ראשית, אנו זקוקים לנתונים!
מודל טוב מתחיל בנתונים טובים. כדי ליצור מודל של מערכת היחסים בין הטורף לטרף, אנו משתמשים בנתוני האוכלוסייה (רשוּמוֹת המפרטות את מִספר החיות). במקרה הזה, קיבלנו את נתוני האוכלוסייה מֵחֶבְרָה שצָּדה הן את הטורפים הן את הנטרפים עבור פרוותם במאות ה-19 וה-20. חברת הדסוֹן בֵּיי (The Hudson Bay Company) האמריקאית ניהלה רשומות שנתיות של מספרי הפרוות שאספו של החיות שֻׁנָּר השלג (להלן: 'שונר'/ 'שונרים') וארנבת השלג (להלן: 'ארנבת'/ 'ארנבים'). באיור 1 ניתן לראות את נתוני החברה לגבי מספרי השונרים והארנבים. נתונים אלה שנאספו, מלמדים אותנו על מספרי האוכלוסייה של כל אחת מהחיות, ויכולים לספֵּק לנו תמונה הגיונית של מערכת היחסים בין הטורף לנטרף. הנתונים מראים כי בשנים מסוימות, כמו 1927, היו יותר שונרים (טורפים), ופחות ארנבים (טרף), בעוד שבשנים אחרות, כמו 1932, היו יותר ארנבים ופחות שונרים.
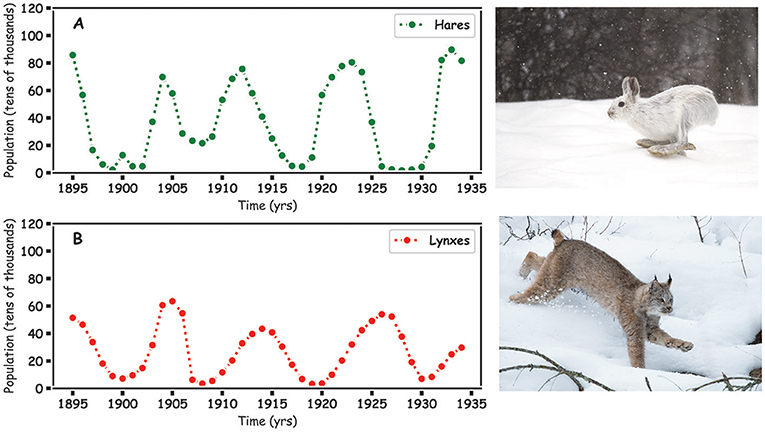
- איור 1 - נתוני מספרי פרוות של ארנבים ושונרים.
- (A) מספר פרוות הארנבת שנאספו (בעשרות אלפים) במשך הזמן. (B) מספר פרוות השונר שנאספו (בעשרות אלפים) במשך הזמן, כפי שנגזר מנתוני חברת הדסון ביי לשנים 19351-1895. Population (tens ofthousands) – אוכלוסייה (בעשרות אלפים); Time (yrs) – זמן (בשנים).
מה מְספרים לנו הנתונים מהדסון ביי?
העליות והירידות שתועדו באוכלוסיות השונרים והארנבים לאורך הזמן רומזות כי יש קשר בין שתי החיות. זה הגיוני, כיוון שאנו יודעים כי שונרים אוכלים ארנבים. האם תוכלו לראות באיור 1 כי אוכלוסיות השונרים והארנבים יורדות ועולות בערך באותו הזמן? כאשר ישנם יותר שונרים, הם אוכלים יותר ארנבים, מה שמקטין את אוכלוסיית הארנבים. כאשר אוכלוסיית הארנבים קטֵנה, המשמעות היא שלשונרים יש פחות מזון, והתוצאה היא ירידה באוכלוסיית השונרים. כאשר אוכלוסיית השונרים מצטמצמת, אוכלוסיית הארנבים גדֵלה שוב, ומחזוֹר העליות והירידות נמשך. אם אוכלוסיות הטורפים והנטרפים מאוזנות, הן יגדלו ויצטמצמו לאורך הזמן, וימשיכו 'לרדוף' זו אחרי זו במעגל החיים. השאלות ששואלים המתמטיקאים הן: 'האם ביכולתנו להסביר זאת באמצעות חיבור, חיסור וכפל?', ו'האם באפשרותנו לחזות את האוכלוסיות העתידיות?'.
מסבירים את מערכת היחסים באמצעות מודלים מתמטיים
מתמטיקאים משתמשים במשוואות דִּיפֵרֶנְצִיָאלִיּוֹת ובנתונים כדי לתאר את מה שהם רואים בעולם. הראשונים שתיארו את מערכת היחסים בין הטורף לטרף באמצעות משוואות דיפרנציאליות, בשנות ה-20 של המאה הקודמת, היו המדען האמריקאי אלפרד לוֹטְקָה (Lotka) [1] והמדען היהודי-איטלקי ויטוֹ ווֹלְטֵרָה (Volterra) [2]. הם רצו להשתמש במתמטיקה כדי להסביר את העליות והירידות שנצפו במערכת היחסים בין הטורפים לנטרפים, באופן כללי.
לעיתים, המשוואות עשויות להיראות מסובכות מאוד, אך הן בסך הכול דרך לתאר איך ומדוע אוכלוסיות משתנות. מתמטיקאי שווייצרי מפורסם בשם לאונרד אוֹילֶר (Leonhard Euler, 1783–1707), הראה כי אפשר לכתוב משוואות דיפרנציאליות רק בתור פלוסים ומינוסים, עם מעט כפל. ניתן להשתמש במשוואות דיפרנציאליות כדי ליצור מודל של אוכלוסיות השונרים (טורפים) והארנבים (טרף), על בסיס הנתונים שסיפקה חברת הדסון ביי. לצורך כך נָזִין את הנתונים המקוריים תוך שימוש בשיטות מתמטיות [3], במטרה להעריך את שיעור הגידול (rgrowth), שיעור התמותה (rdeath), שיעור הנטרפים (reaten), ושיעור המזון (rfood). אלו ישמשו אותנו כדי לחזות את גודל אוכלוסיות הארנבים והשונרים.
יצירת מודל של אוכלוסיית ארנבי השלג
כאשר מתמטיקאים מְפתחים משוואות, הם חושבים על העולם. כעת נחשוב על מה שקורה לאוכלוסיית הארנבים לאורך הזמן. אם לא היו שונרים, אוכלוסיית הארנבים (Hare) בעתיד (Future), HF, הייתה שווה לאוכלוסיית הארנבים הנוכחית (Current), HC. לאחר מכן, אנו מוסיפים את מספר הלידות, וּמְחסרים את מספר מקרי המוות, ומכנים זאת שיעור הגידול (growth), rgrowth. מספר הלידות והמיתות תלוי במספר הארנבים שחיים עכשיו, לכן אנו מכפילים את rgrowth ב-HC (איור 2A).

- איור 2 - משוואות לחיזוי אוכלוסיות הארנבים והשונרים על בסיס שימוש בנתוני חברת הדסון ביי.
-
(A) המשוואות (Equations) המשמשות לִצפות את אוכלוסיית הארנבים העתידית (Future hare population) אם לא היו שונרים. תרחיש זה מתבטא בגדילה מעריכית (Exponential growth). (B) המשוואות המשמשות לִצפות את אוכלוסיית השונרים (Lynx population) אם לא היו ארנבים. תרחיש זה מתבטא בדעיכה מעריכית (Exponential decline). (C) המשוואות עבור אוכלוסיות השונרים והארנבים כאשר יש ביניהן יחסי גומלין (Interaction). תרחיש זה מתבטא בתנודות בגודל שתי האוכלוסיות – השונרים והארנבים. Change in population = שינוי בגודל האוכלוסייה; Years = שנים; Deaths = מיתות; Births = לידות; Steady = יציב; Lost to hunting = אובדן כתוצאה מצַּיִד; Successful hunts = צַיִד מוצלח.
נשתמש בנתונים מטעם הדסון ביי כדי להציב את המספרים בתוך המשוואה. בתחילת איסוף הנתונים, בשנת 1895, אוכלוסיית הארנבים היא 85, לכן נציב: HC = ארנבים 85. שיעור הגידול של אוכלוסיית הארנבים הוא rgrowth = 0.9 בשנה. כיוון שעֵרֶךְ ה-rgrowth חיובי, אנו מצפים כי האוכלוסייה העתידית תִּגדל. כך מתקבלת אוכלוסיית הארנבים העתידית, HF, ב-1896:
HF = HC + (rgrowth × HC), HF = 85 + (0.9 × 85) =161.5.
אנו צופים כי אוכלוסיית הארנבים העתידית תִּמְנֶה 161.5 ארנבים. אם האוכלוסייה הייתה ממשיכה לגדול בצורה כזו, העולם כולו היה מכוסה בארנבים. דפוס זה מכונה גדילה מעריכית (איור 2A).
יצירת מודל של אוכלוסיית השונרים
כעת נבחן מה קורה לאוכלוסיית השונרים בחלוף הזמן. אלמלא היו ארנבים, לשונרים לא היה מזון, ואוכלוסיית השונרים הייתה פוחתת. כדי לתרגם זאת למודל, אנו משתמשים בחיסור. מספר השונרים העתידי (LF), שווה למספר השונרים הנוכחי (LC), פחות שיעור התמותה, rdeath, כפול המספר הנוכחי של השונרים (LC, איור 2B).
אוכלוסיית השונרים ב-1895 היא 51, ועל ידי התאמַת הנתונים אנו קובעים כי שיעור התמותה הוא rdeath = 0.25. כעת תוצאת המשוואה היא:
LF = LC-(rdeath × LC),
LF = 51–(0.25 × 51) = 38.25.
החישוב שלנו מנבא כי אוכלוסיית השונרים העתידית ב-1896 תִּמְנֶה 38.25 פרטים. דפוס זה מוכר כ'דעיכה מעריכית', ואם היה ממשיך להתרחש, לא היו יותר שונרים (איור 2B).
יצירת מודל של יחסי הגומלין בין הארנבים לשונרים
במצב של הִתרבּוּת טבעית, אוכלוסיית הארנבים גדֵלה, ואוכלוסיית השונרים קטֵנה. מה אנו יודעים על יחסי הגומלין בין האוכלוסיות הללו? השונרים טורפים ארנבים ומכאן מדללים את אוכלוסיית הארנבים, לכן, נשתמש בחיסור כדי לייצג זאת במודל. אנו זקוקים למונח המתאר את שיעור הארנבים הנטרפים (eaten), אותו נסמן כ- reaten. שיעור זה תלוי במספר החיות בשתי האוכלוסיות – זו של השונרים וזו של הארנבים – שיכולות לטרוף ולהיטרף, ולכן אנו מכפילים את reaten ב-(LC) וב-(HC).
לפי אותו היגיון, הארנבים הם מקור מזון עבור השונרים. לכן נשתמש בחיבור במשוואת השונרים, ונכפיל את אוכלוסיית הארנבים הנוכחית באוכלוסיית השונרים הנוכחית, כפול שיעור המזון, rfood (איור 2C).
הערכים, HC = ארנבים 85, rgrowth = 0.9, LC = שונרים 51 ו- rdeath = 0.25, נשארים כשהיו. מהנתונים מתקבל שיעור נטרפים של reaten = 0.024, ושיעור מזון של rfood = 0.005. כאשר נציב את המספרים הללו בתוך המשוואה שצופה את מספר הארנבים העתידי, נקבל:
HF = HC + (rgrowth × HC) – (reaten × LC × HC),
HF = 85 + (0.9 × 85) – (0.024 × 85 × 51) = 59.24,
ותוצאות המשוואה שצופה את מספר השונרים העתידי תהיינה עכשיו:
LF = LC-(rdeath × LC) + (rfood × LC × HC),
LF = 51–(0.25 × 51) + (0.005 × 51 × 85) = 59.925.
המודל שלנו, על בסיס שתי המשוואות הנ"ל, צופה כי ב-1896 יחולו הפחתה באוכלוסיית הארנבים ועלייה באוכלוסיית השונרים. זאת כפי שניתן לראות באיור 3, באמצעות החיצים הירוקים והאדומים.
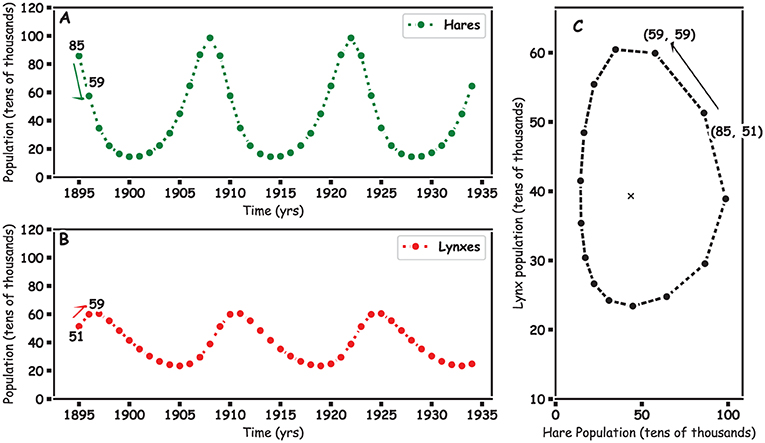
- איור 3 - מודלים של אוכלוסיות הארנבים והשונרים, על בסיס שימוש במשוואות ובנתוני חברת הדסון ביי.
-
(A) מודל של אוכלוסיית הארנבים. (B) מודל של אוכלוסיית השונרים. שני התרשימים הללו מצביעים על מגמות העלייה והירידה שאנו רואים בנתונים האמיתיים באיור 1. (C) האופן שבו אוכלוסיית השונרים משתנה עבור אוכלוסיות שונות של ארנבים. ה-X מייצג את ממוצע אוכלוסיות השונרים והארנבים, אשר סביבוֹ חָגוֹת שתי האוכלוסיות. החיצים והמִּספרים מצביעים על החישובים המוצגים בטקסט, מ-1895 עד 21896. Population (tens ofthousands) – אוכלוסייה (בעשרות אלפים); Time (yrs) – זמן (בשנים).
כדי לִצפות כיצד האוכלוסיות תִּשְׁתַּנֶּינָה בשנה הבאה, 1897, נציב את ערכי HF ו-LF שלנו במשוואות HC ו-LC החדשות. בכל פעם שאנו עושים זאת, אנו מקבלים ערכים חדשים, וכל ערך הוא נקודה בגרפים שלנו באיור 3.
ייצוג חזותי של מערכת היחסים בין הטורף לנטרף
על ידי שימוש במשוואות לעיל בשילוב עם קוֹד מַחְשֵׁב [4], אנו יוצרים ייצוג חזותי של אוכלוסיות השונרים והארנבים. כך אנו מייצרים נתונים משלנו, המראים כיצד מערכת היחסים בין הטורף לטֶּרף מתפתחת לאורך הזמן (איור 3).
דרך נוספת להראות איך שני זַנִּים קשורים זה לזה, היא להציג בתרשים כיצד היחסים משתנים בין אוכלוסיית הארנבים (ציר ה-x) ואוכלוסיית השונרים (ציר ה-y) (איור 3C). ה-x באמצע מייצג את ממוצע אוכלוסיית הארנבים (39), ואת ממוצע אוכלוסיית השונרים (45). הוא ידוע כנקודת שיווי המשקל. אוכלוסיות השונרים והארנבים חָגוֹת סביב הממוצע הזה כשהן עולות ויורדות, ומשׂרטטות תמונה של מעגל החיים. תנועה זו מזכירה את המסלול של כדור הארץ סביב השמש. האוכלוסיות ממשיכות לחוג סביב, מה שמייצג את עליותיהן ומורדותיהן במהלך הזמן. במערכת אקולוגית מאוזנת, כמו זו שמוצגת במודל שלנו, מסלול ההקפָה נותר יציב. אולם אם המסלול מתחיל להתפתל פנימה או החוצה, הדבר עשוי להיות סימן מקדים לשינוי.
שינוי שכזה התרחש ב-1995, כאשר השיבו את הזאבים לפארק הלאומי ילוֹסטוֹן (Yellowstone) בארה''ב. לצעד זה היו השלכות מפתיעות על המערכת האקולוגית המקומית3. בהתבסס על התצפיות המדהימות הללו ועל חישובים מתמטיים, אשר דומים לאלו שהצגנו כאן, גוּדְמַן (Goodman) ועמיתיו פיתחו משחק מַחשב שמטרתו לבנות מערכת אקולוגית מאוזנת4.
מודלים אינם דבר מדויק
כאשר מתמטיקאים מנסים לתאר משהו מורכב, הם מְפשטים דברים. גם המשוואות שהצגנו חייבות לפשֵּׁט את המודל. כאשר עושים זאת, המשמעות היא שהתחזיות וההדמיות אינן תואמות באופן מושלם את הנתונים המקוריים. הנה מידע שהשמטנו מהמודל שלנו:
• יש יותר מאשר טורף אחד הניזון מארנבי השלג.
• שונרי השלג לא צדים רק ארנבי שלג; הם יכולים לאכול גם דגים וסנאים.
• במודל שלנו, לארנבי השלג תמיד יש אוכל – מה שאינו נכון בחורף.
• מה לגבי אנשים, ציידי פרוות, שצדים הן את השונרים הן את הארנבים?
כדי לגרום למשוואות להיות ישׂימוֹת בכל המצבים האחרים הללו, נצטרך לכלול משוואות נוספות, ופעולות חיבור וחיסור נוספות. אם כל הנתונים יהיו ברשותנו, נוכל ליצור מודל מושלם של העתיד. אפילו כאשר מְפשטים את הדברים, המתמטיקה משמשת אותנו בצורה יעילה ליצירת מודלים של אוכלוסיות הארנבים והשונרים.
באלה אֳפָנִים נוספים ניתן להשתמש במודל זה?
במודל שפיתחנו, תוכלו לשנות את המילה 'שונר' למילה 'כריש', ואת המילים 'ארנבת שלג' ל'דג' – עם הנתונים הנכונים, המתמטיקה תעבוד בכל מקרה [2]. תוכלו אפילו להשתמש באותן משוואות ולשנות את המילה 'שונר' ל'זוֹמבּי' ואת 'ארנבת שלג' ל'בן אדם'! אפשר להרחיב את מערכת היחסים בין הטורף לטֶּרף אף מֵעֵבֶר לאוכלוסיות בעלי החיים, ולהשתמש במודל כדי לתאר מערכות יחסים בין חֲבָרוֹת; התרחשות תגובות כימיות בין חומרים, והתפשטות של נגיפים. תוכלו לקרוא עוד על המתמטיקה של נגיפים בכתבה אחרת של פרונטירז – מדע לצעירים, בקישור שבמקור [5].
סיכום
כדי לפתֵּח מודלים של העולם האמיתי, מתמטיקאים צריכים להתחיל מנתונים טובים. כלומר חיוני שמדענים; אנשים העוסקים בשימור – ואפילו ציידים! – יאספו מידע מסביבתם. באמצעות שימוש בנתונים, אנו מצליחים לזהוֹת דפוסים במערכות יחסים. אז באפשרותנו להשתמש במתמטיקה כדי ליצור מחדש את הדפוסים הללו ולחזות נתונים עתידיים, שיכולים לייצג את אותן מערכות יחסים, ולחזות את עתידן. תחזיות אלה יכולות לסייע לנו לשמֵּר את האיזון במערכות אקולוגיות. אנו מקווים כי המאמר המחיש לכם שנדרשים רק מתמטיקה בסיסית (חיבור, חיסור וכפל), וקצת חשיבה נבונה, כדי ליצור מודלים ולחזות אוכלוסיות של טורפים, של נטרפים, והרבה יותר מכך.
מילון מונחים
משוואות דִִּיפֵרֶנְצִיאָלִיּוֹת (Differential Equations): ↑ משוואות המתארות איך אוכלוסיות משתנות במהלך הזמן, או תהליכים רבים אחרים. עם אלה נמנים למשל: כיצד מסוֹק טס; איך כוכבי-לכת חָגִים סביב כוכב; וכיצד הדם זורם בוורידים שלנו.
הַעֲרָכָה (Estimate): ↑ עֵרֶךְ הקרוב מספיק לתשובה המדויקת. הערָכה מתגבשת בדרך כלל בהתבסס על יֶדַע מסוים שיש לכם לגבי המערכת, או על ידי ביצוע חישובים.
שיעור הגידול (Growth Rate): ↑ הַצְּמיחה באוכלוסיית הארנבים אלמלא היו להם טורפים. ניתן להעריך אותו מהנתונים, כאשר מפחיתים את מִספר מקרי המוות ממִּספר הלידות.
שיעור התמותה (Death Rate): ↑ הדעיכה באוכלוסיית השונרים לאורך הזמן, לוּלֵא היה להם מזון. זהו מִספר מקרי המוות, פחות מִספר הלידות.
שיעור הנטרפים (Eat Rate): ↑ מִספר הארנבים שניצודו ונאכלו על ידי השונרים.
שיעור המזון (Food Rate): ↑ מִספר הארנבים שהשונרים צריכים לאכול כדי לשרוד.
גדילה מעריכית (Exponential Growth): ↑ צמיחה יציבה ומהירה.
נקודת שיווי המשקל (Equilibrium Point): ↑ נקודת האיזון בין שתי האוכלוסיות. כאשר מערכת מצויה באיזון, אנו אומרים שהיא יציבה.
הצהרת ניגוד אינטרסים
המחברים מצהירים כל המחקר נערך בהעדר כי קשר מסחרי או פיננסי שיכול להתפרש כניגוד אינטרסים פוטנציאלי.
תודות
עבודה זו זכתה למימון מטעם מועצת המחקר האירית (GOIPG/2020/943).
הצהרת כלי בינה מלאכותית
טקסט חלופי הנלווה לאיורים במאמר זה נוצר על ידי פרונטירז בסיוע כלי בינה מלאכותית, ונעשו מאמצים על מנת להבטיח את דיוקו, כולל בדיקה על ידי כותבי המאמר כאשר הדבר התאפשר. אם ברצונכם לדווח על בעיה, אנו צרו איתנו קשר.
הערות שוליים
1. ↑לחצו כאן לגרסה מונפשת של האיור.
2. ↑לחצו כאן לגרסה מונפשת של האיור.
3 ↑צְפוּ: Sustainable Human 2014.
מקורות
[1] ↑ Lotka, A. J. 1920. Analytical note on certain rhythmic relations in organic systems. Proc Natl Acad Sci USA. 6:410–5.
[2] ↑ Volterra, V. 1926. Fluctuations in the abundance of a species considered mathematically. Nature. 118:558–60.
[3] ↑ de Silva, B. M., Champion, K., Quade, M., Loiseau, J. C., Kutz, J. N., and Brunton, S. L. 2020. PySINDy: a python package for the sparse identification of nonlinear dynamics from data. arXiv Preprint arXiv:2004.08424.
[4] ↑ Butler, J. S., and Brady, R. M. 2020. Predator Prey Code for Young-Minds. GitHub. Available online at: https://github.com/john-s-butler-dit/Predator-Prey-for-Young-Minds
[5] ↑ Brooks, H. Z., Kanjanasaratool, U., Kureh, Y. H., and Mason. P. 2021. Disease detectives: using mathematics to forecast the spread of infectious diseases. Front Young Minds. 9:577741. doi: 10.3389/frym.2020.577741
