תַקצִיר
מתמטיקה היא התחום המדעי האובייקטיבי ביותר שֶׁקַיָּם. מה שנכון היום במתמטיקה, לָעַד יישאר בה נכון, ולוויכוחים מתמטיים תמיד תהיינה הכרעות מובהקות לצד זה או אחר. אלה תכונות שאני אוהב מאוד במתמטיקה, מאז שהייתי ילד. במאמר זה, אנסה לְשַקֵּף לכם את יופייה של המתמטיקה, ואראה לכם שהיא מופיעה במצבים רבים בחיינו – גם במקומות שאולי לא היינו מצפים לכך. לאחר מכן, אתן לכם טעימה משני מחקרים שערכתי בתחום מתמטי שנקרא קוֹמְבִּינָטוֹרִיקָה, ואסביר כיצד הם קשורים לבעיות שאנו נתקלים בהן ביומיום. אחת הבעיות האלה היא לדוגמה איך לבצע ניתוח מתמטי מדויק של זרמי נתונים גדולים שאיננו יכולים לשמור בזיכרון המחשב, באופן שיאפשר לנו להעריך תכונות סטטיסטיות שלהם. לבסוף, אנסה לספֵּק לכם מבט מעשׂי על חַיַּי כמתמטיקאי – האתגרים והקשיים שבהם, לצד ההנאות והסיפוק הגדולים שאני מפיק מהם.
פרופסור נוגה אלון זכה בפרס גֶּדֶל במדעי המחשב לשנת 2005, במשותף עם פרופסור יוסי מטיאס ופרופסור מריוֹ סגדי, עבור עבודה שהניחה את היסודות לניתוח של זרמי נתונים באמצעות זיכרון מוגבל. בשנת 2022 זכה פרופסור אלון בפרס שאו במתמטיקה, במשותף עם פרופסור אהוד הְרוּשׁוֹבסקי, עבור תרומותיהם יוצאות הדופן למתמטיקה דיסקרטית ולתורת המודלים עם אינטראקציה במיוחד לגיאומטריה אלגברית, טוֹפּוֹלוֹגְיָה ומדעי המחשב.
הקדמה – על יופייה של המתמטיקה
מתמטיקה היא תחום יֶדַע שיכול לעורר באנשים תחושות חזקות של משיכה או רתיעה. יש אנשים שאוהבים מאוד מתמטיקה כבר מגיל צעיר. אני לדוגמה ידעתי כבר בגיל 8 או 9 שאֶרצה להיות מתמטיקאי כשאהיה גדול. איני סבור שכל האנשים צריכים לאהוב מתמטיקה או להיות מתמטיקאים (למעשה, אני אפילו חושב שמצבהּ של האנוֹשוּת לא יהיה טוב כל כך אם מַרבית האנשים יעסקו בתחום זה). בכל זאת, אני מוצא שבמתמטיקה יש הרבה יופי, שכל אחד ואחת יכולים ללמוד להבחין בו ולהעריכו – מקרוב או מרחוק.
עבורי מתמטיקה היא בראש ובראשונה דרך חשיבה הגיונית ואובייקטיבית שבאמצעותה אני מנסה להבין תהליכים לוגיים, או תהליכים שמתרחשים בעולם. אחד הדברים שאני אוהב במיוחד במתמטיקה הוא כאמור האובייקטיביוּת שלה. בוויכוחים מתמטיים, צד אחד יכול לשכנע את הצד האחר שהטיעון שלו נכון, והצד האחר באמת ישתכנע, כיוון שהמתמטיקה עצמה תשכנע אותו. דבר זה אינו מתרחש במקרים אחרים של חילוקי דעות (חִשְׁבוּ למשל על ויכוחים פוליטיים – כמעט לא קורה שצד אחד משכנע את הצד האחר בצדקתו כך שהצד האחר מחליט לשנות את דעתו). במתמטיקה יש גם מֵמַד של יציבוּת – מה שנכון עכשיו נשאר נכון תמיד, ומה שלא נכון עכשיו תמיד יישאר לא נכון. בתחומי מדע אחרים, בכללם פיזיקה לדוגמה, אין זה בהכרח נכון – תיאוריות המְּתארות את המציאוּת עשויות להשתנות, ופעמים רבות אכן הן משתנות בחלוף הזמן.
היבט נוסף שאהוב עליי במתמטיקה הוא האתגר הטמון בה. בתור מתמטיקאי אני מנסה לפתור חידות. לְחֵלֶק מהחידות אני יודע מראש שיש פתרון ומבקש למצוא אותו, ולחידות אחרות אפילו איני בטוח אם קיים פתרון. לא פעם, לְשֵׁמַע חידה כזו אני עשוי להרגיש שאין לי סיכוי לפתור אותה. אבל אז אני חושב עליה רבּוֹת, ומנסה כל מיני דרכים וגישות לפתרון, ופתאום מגיעה לי איזושהי הברקה. לא תמיד אני יודע להסביר מה גרם לזה, ולמה זה קרה דווקא עכשיו (חצי שעה אחרי שהתחלתי לחשוב על החידה, או שבועות וחודשים לאחר מכן). פתאום אני יודע משהו חדש שלא ידעתי קודם, ותהליך זה של התגברות על האתגר הראשוני ופיצוחה של החידה המתמטית מֵסֵב לי סיפוק רב.
לפעמים אני אפילו חושב על מתמטיקה כעל אומנות, כי היא ניחנה ביופי בפני עצמה. ישנם חלקים במתמטיקה שהם יישׂומיים יותר, ומשמשים תחומי מדע אחרים כמו למשל פיזיקה, כימיה וביולוגיה, כדי להסביר באמצעותם את המציאוּת שלנו. לצידם ישנם במתמטיקה גם חלקים מופשטים שבהם מגדירים מבנים מתמטיים שונים שאין להם בהכרח קשר למציאות שאנו מכירים. לעיתים כן מתגלה קשר כזה בדיעבד, אבל בעיניי למתמטיקה יש עֵרֶךְ פנימי שאינו תלוי בשאלה אם היא מתארת משהו במציאות. כמו אומנות מופשטת – שאינה עוסקת בפריטים מוחשיים בעולם הפיזי והיא אסתטית (כלומר, יפה ונעימה לעין), גם מתמטיקה מופשטת היא אסתטית וּמְספקת לנו חוויה של יופי.
מתמטיקה מופיעה בחיינו במקומות מפתיעים
מתמטיקה אינה מוגבלת רק לבעיות שאנו פותרים על נייר בשיעורי אלגבּרה וגיאומטריה. לעיתים קרובות היא מופיעה בליבן של תופעות שאנו פוגשים בחיי היומיום. בתור דוגמה, אתאר לכם את סיפורו של סוציולוג הונגרי בשם שנדור סאלאי (Sandor Szalai), שחי ופעל במאה שעברה. סאלאי ערך ניסויים על יחסי חברוּת בין ילדים. הוא שאל כל זוג ילדים אם הם חברים או לא, כאשר עבור כל זוג היחס היה סִימֶטְרִי – כלומר, אם האחד אמר שהם חברים אז גם האחר/ת אמרו שהם חברים, ולהפך (במילים אחרות, לא היה מצב שבו אחד אמר שכּן ובן/ בת הזוג אמרו שלא). סאלאי גילה כי באופן עקבי בכל פעם שהיו בקבוצה שמונה עשר ילדים לפחות, תמיד היו מתוך הקבוצה הזו ארבעה ילדים שכל זוג מתוכם (סך הכול יש שישה זוגות כאלה) היו כולם חברים, או שהיו כולם לא חברים. סאלאי שמח כי חשב שמדובר בתגלית סוציולוגית חדשה ומלהיבה. לאחר שיחה עם חבריו המתמטיקאים, התברר לו כי כְּלל לא מדובר בתגלית סוציולוגית אלא בעובדה מתמטית! מתברר כי המצב שסאלאי חקר הוא מקרה פרטי של תורה מתמטית בשם 'תורת רמזי' (Ramsey's theorem). תורת רמזי גורסת כי במצבים כלליים ביותר לא ניתן לקבל אי-סדר מוחלט. כלומר, שכּל מערכת מספיק גדולה מכילה תת-מערכת שהיא מסודרת מאוד.
כדי להסביר את הרעיון הזה על הדוגמה שלנו, נוכל לייצג כל ילד בתור נקודה על דף, ולחבּר כל זוג נקודות בקו כחול, שנבחר כמסמֵּן שהילדים חברים, או בקו אדום, שנבחר כמסמֵּן שהילדים לא חברים. בסך הכול נקבל שמונה עשרה נקודות שכּל זוג מהן מחובר בקו כחול או בקו אדום. לפי תורת רמזי, לא משנה איך נצבע את הזוגות האלה, תמיד נקבל ארבע נקודות שכל הזוגות ביניהן צבועים באדום או ארבע נקודות שכל הזוגות ביניהן צבועים בכחול. אם כן, התוצאה הזו של קיום ארבעה ילדים מתוך שמונה עשר שעבורם כל הזוגות חברים או לא חברים היא תוצאה מתמטית, לא סוציולוגית.
תוכלו לערוך תרגיל קטן, ולבדוק מה קורה בסיטואציה דומה עם שישה ילדים. נַסּוּ לחבּר כל זוג מבּין שש נקודות על דף באמצעות קווים כחולים ואדומים. תגלו שלא משנה איך תמתחו את הקווים, בכל מקרה תקבלו משולש כחול או משולש אדום, או גם משולש אדום וגם משולש כחול (איור 1). לסקרנים שביניכם, נסו להוכיח כי אם לוקחים 5 ילדים, אין זה כך – לא חייבים לקבל משולש כחול או משולש אדום.

- איור 1 - מתמטיקה חברתית.
- אם נסתכל על שישיית ילדים שכל זוג ביניהם יכולים להיות או חברים (קו כחול) או לא חברים (קו אדום), נקבל בהכרח כי שלושה מתוכם כולם חברים (משולש כחול) או/גם כי שלושה מתוכם כולם לא חברים (משולש אדום). זוהי תוצאה מתמטית שמשפיעה על מבנים חברתיים.
קומבינטוריקה – שתי דוגמאות על גנבים ושכחנים
אחד התחומים העיקריים שאני עוסק בהם במתמטיקה נקרא קומבינטוריקה. מבחינה פורמלית קומבינטוריקה היא המתמטיקה של מבנים סופיים (בניגוד למתמטיקה רציפה שעוסקת במבנים לא סופיים) [1]. לְשֵׁם פשטוּת, חִשְׁבוּ על המבנים האלה בתור אוסף של עצמים. בקומבינטוריקה, אנו עוסקים בקבוצות סופיות של עצמים, ומנסים להבין מה התכונות שלהן. בדוגמת הילדים שהובאה קודם, קבוצה היא אוסף של נקודות שחלקן מחוברות בכחול, וחלקן מחוברות באדום. קומבינטוריקה קלאסית עוסקת בשאלות כמו: כמה אפשרויות ישנן לְסַדֵּר עשרה ילדים בשורה זה לצד זה? וכן, כמה אפשרויות ישנן לִבְחֹר עשרה ילדים מתוך קבוצה של חמישים ילדים? ביכולתנו גם לשאול שאלות מורכבוֹת יותר, כמו למשל: האם אנו יכולים לבחור מתוך קבוצה של שבעה ילדים שבע שְׁלָשׁוֹת כך שלכל זוג שְׁלָשׁוֹת יהיה בדיוק ילד אחד המשותף לשלישייה האחת ולשלישייה האחרת, ולכל שני ילדים בקבוצה תהיה בדיוק שלישייה אחת שמכילה אותם? דוגמה נוספת לשאלה קומבינטורית על מבנה שאתם אולי מכירים, קשורה למשחק סוּדוֹקוּ. נוכל למשל לשאול את עצמנו כמה ריבועי סודוקו שונים ישנם עבור ריבוע סודוקו בגודל 30X30.
בקומבינטוריקה מודרנית, אנו עוסקים בבעיות קיצון, ושואלים את עצמנו מה הגודל הגדול ביותר או הקטן ביותר של מבנה קומבינטורי שמקיים תכונות מסוימות. לשאלות כאלה ישנם שימושים רבים במדעי המחשב, וגם בתחומים אחרים של מתמטיקה כמו למשל גיאומטריה או תורת המִּספרים. כעת, אציג לכם שתי דוגמאות לחידות קומבינטוריות שאותן חקרתי.
גנבים הוגנים
אחת הבעיות שבהן התעמקתי בקריירה שלי, עוסקת בחלוקה הוגנת של מחרוזות. חִשְׁבוּ על מקרה שבו גנבים (בעלי כישורים מתמטיים) גונבים שרשרת עם שני סוגי אבני חן – יהלומים ואבני אודם (איור 2). הגנבים הם הוגנים, ומחליטים שכל אחד מהם יקבל מספר זהה של יהלומים ושל אבני אודם. בתהליך חלוקת הַשָּׁלָל הם רוצים לחתוך את השרשרת לכמה שפחות חלקים. נשאלת השאלה – כמה חתכים (לכל הפחות) הם צריכים לבצע כדי לחלֵּק ביניהם את השרשרת בצורה הוגנת?

- איור 2 - חלוקה הוגנת של מחרוזת המורכבת מיהלומים ומאבני אודם.
- נניח ששני גנבים גונבים שרשרת המורכבת מיהלומים ומאבני אודם, והם רוצים להתחלק בשלל שווה בשווה. כמה חתכים לכל הפחות הם יצטרכו לבצע במחרוזת כדי להתחלק בשלל באופן שווה? האם אתם רואים כי במקרה של איור זה מספיק שיבצעו חתך אחד כזה?
קל לראות שאם האבנים בשרשרת היו מסודרות כשסוג אחד נמצא בצד אחד והסוג השני בצד האחר, היו מספיקים שני חתכים כדי לחלֵּק את השלל באופן הוגן (איור 3A). כעת נוכיח כי גם אם האבנים בשרשרת לא מסודרות בצורה מיוחדת אלא בצורה אקראית, עדיין מספיקים שני חתכים כדי לחלֵּק את השלל באופן הוגן. נניח שבשרשרת יש לנו שמונה יהלומים ושש אבני אודם. כדי שהחלוקה תהיה הוגנת, על כל גנב לקבל ארבעה יהלומים ושלוש אבני אודם.
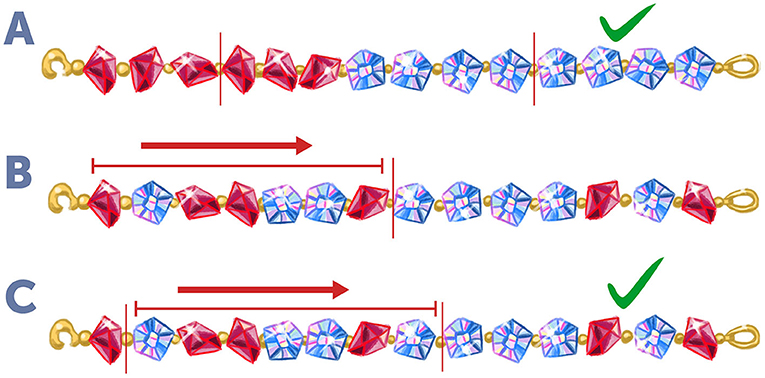
- איור 3 - חלוקה הוגנת של מחרוזת המורכבת משני סוגי אבנים יקרות.
- (A) אם ניקח שרשרת שבה שש אבני אודם שמסודרות בצד שמאל ושמונה יהלומים שמסודרים בצד ימין, קל לראות שיספיקו שני חתכים במחרוזת (קווים אנכיים באדום) כדי לקבל חלוקה הוגנת של השרשרת. ואכן, בין שני החתכים נקבל שלוש אבני אודם וארבעה יהלומים, וכך גם בחלקים משמאל ומימין לשני החתכים. (B) עבור שרשרת בעלת אותה כמות של אבני אודם ויהלומים כמו ב- A שמסודרת בצורה אקראית, ניתן לראות שחתך אחד באמצע יצור מצב של יותר מדי אבני אודם ופחות מדי יהלומים בצד שמאל, לעומת פחות מדי אבני אודם ויותר מדי יהלומים בצד ימין. (C) אם נזיז את החתך אבן אחת ימינה ונוסיף חתך אחרי האבן הראשונה משמאל, נוסיף למעשה יהלום אחד ונוריד אבן אודם אחת מהקטע האמצעי בשרשרת. כעת נקבל מצב שבו בתוך הקטע שבין שני החתכים ומחוצה לו יש מספר זהה של שלוש אבני אודם וארבעה יהלומים. כלומר, גם עבור השרשרת האקראית מספיקים שני חתכים כדי לחלֵּק את האבנים היקרות באופן שווה לשני אנשים.
נתחיל ממצב שבו היהלומים ואבני האודם מסודרים בצורה אקראית לאורך השרשרת (איור 3B). בתור התחלה, נחתוך את השרשרת באמצע ונבחין בכך שיש לנו יותר מדי אבני אודם בצד שמאל (ארבע אבנים), ומעט מדי אבני אודם בצד ימין (שתי אבנים). כעת, ניקח את מִקְטַע החיתוך שלנו ונזיז אותו מקום אחד ימינה באמצעות חתך נוסף (איור 3C). הזזַת החתך כולו מקום אחד ימינה גרמה לכך שיתווסף יהלום אחד מצד ימין, ותוחסר אבן אודם אחת מצד שמאל (איור 3C). אם נספור כעת את כמות האבנים בין שני הקווים האדומים (השלל של הגנב הראשון) ומחוץ לשני הקווים האדומים (השלל של הגנבת השנייה), נראה כי בשני המקרים קיבלנו כמות זהה של ארבעה יהלומים ושלוש אבני אודם. הצלחנו לחלֵּק את השרשרת בצורה הוגנת באמצעות שני חתכים!
עתה נכליל את המקרה הפרטי שבחנּוּ לעיל, למקרה כללי שבו ישנהּ מחרוזת עם כמות זהה של אבנים מכל סוג, המסודרות לאורך השרשרת בצורה אקראית. נבחר תחילה מקטע חיתוך בין קצה השרשרת לאמצעהּ. בכל הזזה ימינה שאנו מְבצעים עם מִקטע החיתוך שלנו, אנו מוותרים על אבן אחת מצד שמאל, ומרוויחים אבן אחת מצד ימין משום שכמות האבנים צריכה להישאר זהה (במקרה שתואר מקודם, החתך מכיל תמיד שבע אבנים – מחצית מתוך ארבע עשרה האבנים שישנן). כלומר, יש לנו סך הכול ארבע אפשרויות לְמָה שיִקרה אחרי התזוזה:
1. נפסיד אבן אודם מצד שמאל ונקבל אבן אודם מצד ימין
2. נפסיד יהלום מצד שמאל ונקבל יהלום מצד ימין
– בשני המקרים האלה מספר אבני האודם בתוך המקטע שלנו יישאר כשהיה –
3. נפסיד אבן אודם מצד שמאל ונקבל יהלום מצד ימין – אז תהיה לנו אבן אודם אחת פחות מאשר לפני ההזזה
4. נפסיד יהלום מצד שמאל ונקבל אבן אודם מצד ימין – אז תהיה לנו אבן אודם אחת יותר.
תוכלו לראות שבכל מקרה מספר אבני האודם שיש ברשותנו יכול להשתנות רק ב-1 אחרי ההזזה. אם נתחיל למשל במצב שבו בחצי השמאלי של השרשרת יש לנו יותר מדי אבני אודם, ונזיז את המקטע כל הדרך עד לחצי הימני של השרשרת, בהכרח נקבל מצב שבו יש לנו פחות מדי אבני אודם (כי אז חזרנו למצב ההתחלתי, שבו מצד שמאל היו יותר מדי אבני אודם, ומצד ימין היו פחות מדי אבנים).
אם נתחיל במצב של יותר מדי אבני אודם בצד אחד, ונסיים במצב של פחות מדי אבני אודם בצד הזה, כאשר כל פעם שינינו את המצב בלא יותר מאבן אודם אחת – הרי בטוח שבשלב כלשהו בדרך נגיע למצב שבו יש לנו מספר זהה של אבני אודם בשני הצדדים (ובאופן אוטומטי גם מספר זהה של יהלומים בשני הצדדים). זו תוצאה של משפט מתמטי בשם משפט ערך הביניים הדיסקרטי, שלפיו אם משהו מתחיל מֵעֵרֶךְ גדול מדי, מסיים בערך קטן מדי, ומשתנה במעט על ידי הזזה קטנה בכל פעם – בדרך נקבל בהכרח את הערך שאנו רוצים.
במקרה הכללי של אותה בעיה, אנו יכולים לחשוב על מספר כלשהו של גנבים, שנסמן אותו ב-k, ומספר כלשהו של סוגי אבנים, שנסמן אותו ב-t. מה שאני הוכחתי הוא שבכל מקרה כזה שבו אנו רוצים לחלֵּק שרשרת עם t סוגי אבנים שווה בשווה בין k גנבים, מספיק לבצע בשרשרת (k-1)•t חתכים כדי לחלֵּק את השלל בצורה הוגנת [2]. במקרה הפשוט שראינו קודם היו k=2 גנבים ו-t=2 סוגי אבנים, ויכולנו לחלק את השלל באמצעות 2 = (2-1)•2 חתכים. באותו אופן, אם נחשוב על מקרה של ארבעה גנבים ושני סוגי אבנים, נוכל לחלק את השלל בצורה הוגנת על ידי 6 = (4-1)•2 חתכים. דוגמה מפורטת יותר על המקרה של ארבעה גנבים ושני סוגי אבנים, והסבר אינטואיטיבי על ההוכחה למקרה הכללי, ניתן לראות בסרטון זה. חשוב להבין שההוכחה למקרה הכללי היא מורכבת, ואינה נובעת באופן פשוט וישיר מההוכחה למקרים של שני גנבים או של ארבעה גנבים. לעיתים קרובות זה כך במתמטיקה – לא מספיק רק לחשוב בהיגיון ולטעון טענות אינטליגנטיות, אלא צריך גם להשתמש בשיטות ובכלים שדורשים יֶדַע והבנה רבים. במקרה שלנו, ההוכחה של חלוקת שרשרת בצורה הוגנת דורשת שימוש בשיטות מתמטיות מתקדמות, לרבּות שימוש בכלים מתחום במתמטיקה שנקרא טוֹפּוֹלוֹגְיָה.
הבעיה הזו שתיארתי לכם במונחים של חלוקה הוגנת של שרשרת אבנים יקרות, תְּקֵפָה גם למצבים אחרים מחיי היומיום. תוכלו לחשוב למשל על המצב של פריסת עוגה ארוכה שעל חלקים שונים בה יש שוקולד, סוכריות והפתעות נוספות, ואנו מעוניינים לחלקהּ בין אנשים כך שכל אחד יקבל את אותה הכמות מכל אחת מהתוספות שעל העוגה. אם נחפש דוגמה עתיקה יותר מההיסטוריה, נוכל לחשוב על מקרה שבו מבקשים לחלֵּק חלקת אדמה בין אנשים שונים, כאשר החלקה מורכבת מסוגים שונים של קרקע (קרקע חקלאית, קרקע טבעית, קרקע לבנייה). במקרה כזה, כיוון שחלוקת הקרקע דורשת משאבים, אך גם היות שרוצים שכל אדם יקבל חלקת אדמה גדולה ככל האפשר (ושצורתה לא מסובכת מדי), הגיוני ששואפים לתת לכל אדם חלק שקול מבחינת סוגי הקרקע, בלי לחלק את הקרקע ליותר מדי חלקים.
בעיות מודרניות בכיוון זה עוסקות בשאלה של חלוקת משאבים. במקרה הזה, יש לנו אוסף כלשהו של משאבים לחלוקה בין אנשים, אבל לכל אדם יש העדפות שונות ודעות שונות לגבי הערך של כל משאב. השאיפה שלנו היא לחלק את המשאבים השונים בין האנשים כך שהחלק שכל אדם מקבל יהיה זהה מבחינת הערך האישי שהוא מעניק למשאבים האלה (לדוגמה, אדם מסוים יקבל חלק שהוא מעדיף, אך שאולי עשוי פחות ' 'למצוא חן'' בעיני אדם אחר). באופן הזה, אף אדם לא יקנא בזולתו, וכולם יהיו מרוצים ממה שהם מקבלים. בשאלות כאלה בין השאר עוסקת תורה במתמטיקה שנקראת תורת המשחקים האלגוריתמית.
שכחנים מתוחכמים
בעיה נוספת שעסקתי בה בעבודתי היא סוגיה מעניינת במדעי המחשב שקשורה לאלגוריתמים לטיפול במידע זורם. במקרה כזה, מגיע אלינו אוסף גדול מאוד של נתונים – כל כך גדול שאיננו יכולים לשמור אותו בזיכרון המחשב (חִשְׁבוּ למשל על תעבורת מידע באינטרנט), אלא רק לקרוא אותו בזמן שהוא עובר דרך המחשב. אחת השאלות שעסקתי בהן היא: אֵילוּ תכונות סטטיסטיות של המידע הזה אנו יכולים לדעת למרות שאין באפשרותנו לזכור אותו במחשב [3]. ישנם דברים שאנו מסוגלים לדעת על המידע הזה בלי לשמור אותו, ויש דברים אחרים שלא, ואין זה תמיד ברור ממבט ראשון. אמחיש לכם זאת באמצעות דוגמה: אני עומד להגיד לכם עכשיו את כל המספרים השונים בין 1 ל-100 בסדר אקראי, חוץ ממספר אחד שאשמיט בכוונה. לכם אסור לכתוב את המספרים, ואתם גם לא תצליחו לזכור את כולם. השאלה שלי היא האם ישנהּ דרך שבה תוכלו בסוף לומר לי איזה מספר השמטתי, בלי לזכור את המספרים עצמם? חִשְׁבוּ על כך קצת לפני שתמשיכו לפתרון.
התשובה היא שכּן. אתם יכולים לגלות איזה מספר הושמט בלי לזכור את כל המספרים. הנה הפתרון: כל מספר שאגיד לכם, תְּחַבְּרוּ למספר הקודם שאמרתי ותקבלו סכום. אם אגיד לכם 7 אתם תִּזְכְּרוּ 7, אחר כך אגיד 8 ואז תחברו 7+8 ותזכרו 15. אחרי כן אגיד לכם 22, תחברו ל-15 ותזכרו 37, וכן הלאה. בסוף התהליך תקבלו את הסכום של כל המספרים שאמרתי לכם. את הסכום הזה תוכלו לחסֵּר מהסכום של כל המספרים בין 1 ל-100, שאותו אגב אתם יכולים לחשב בדרך פשוטה יחסית כסכום של 50 זוגות, כשערכּוֹ של כל זוג הוא (50+51 ....98+3, 99+2, 100+1) 101. כלומר, סכום כל המספרים בין 1 ל-100 הוא 5,050 = 101•50. ההפרש שתקבלו מחיסור סכום המספרים שאמרתי לכם מ-5,050 הוא בדיוק המספר שהשמטתי מסדרת המספרים! במקרה הזה, הצלחתם לענות על שאלה חשובה שקשורה במידע שקיבלתם, בלי שהייתם צריכים לזכור אותו.
השאלות שאני עוסק בהן מתייחסות לאוספים של מספרים גדולים מאוד, שבקלות יכולים להגיע לערכים של טריליונים (טריליון אחד הוא מיליון מיליון, או הספרה 1 שאחריה מופיעים 12 אפסים). אין באפשרותנו לשמור כמויות כאלה של מספרים גדולים בזיכרון המחשב, ולכן עלינו למצוא מה אנו כן יכולים לדעת עליהם בלי לשמור אותם. מתברר למשל, שאם אנו רוצים לדעת אם מבּין כל המספרים שעברו יש מספר שהגיע פעמיים – לא נוכל לעשות זאת בלי לזכור את כל המספרים. אבל, אם אנו רוצים לדעת בערך כמה מספרים שונים זה מזה הגיעו, יש דרך שבה נוכל לעשות זאת בלי לזכור את המספרים עצמם [3] – רְאו הדגמה רעיונית לכך באיור 4. לא אפרט את הדרך להראות זאת כאן, מאחר שהיא מעט מסובכת, אבל אציין שבמקרה כזה יש באפשרותנו לבצע הערכה הסתברותית שבה, בהסתברות גבוהה (כלומר ברוב המוחלט של המקרים), נקבל תוצאה קרובה מאוד לתוצאה האמיתית, ובהסתברות קטנה (רק במעט מאוד מקרים) נקבל תוצאה שאינה מאוד קרובה לתוצאה האמיתית. ייתכן למשל שבהסתברות של 99% (כלומר, ב-99 מקרים מתוך 100) נקבל תוצאה שטועה בפחות מ-1% ביחס לתוצאה האמיתית, ובהסתברות של 1% (כלומר במקרה 1 מתוך 100), נקבל תוצאה שאינה קרובה לתוצאה האמיתית. כפי שאתם מבינים, המתמטיקה שאני עוסק בה מאפשרת לנו להגיע לתוצאות מפתיעות ובלתי צפויות, וזה חלק נוסף ביופי שלה – לְאַפשר לנו להתרחב אל מֵעֵבֶר לאינטואיציה הראשונית שלנו.

- איור 4 - אלגוריתמים לטיפול במידע זורם.
- ישנם מצבים שבהם אנו נדרשים להתמודד עם כמויות אדירות של מידע שמגיע אלינו, ואין באפשרותנו לשמור את כולו במחשב, כמו למשל מידע שזורם ללא הפסקה באינטרנט (מתואר באופן פשוט) על ידי זרימת הכדורים הרבים שבאיור. כדי להצליח להסיק משהו חשוב לגבי המידע הזה, בלי לשמור אותו, עלינו להשתמש ב'תכסיסים' מתמטיים שונים (מימין למטה) המאפשרים לנו, בהסתברות גבוהה, לקבל תוצאה קרובה לתוצאה האמיתית – אותה איננו יכולים לחשֵּׁב במדויק בלי לשמור את המידע כולו.
העבודות האלה הניחו את היסודות לניתוח מתמטי מסודר של זרמי נתונים בכמות גדולה מאוד ('בִּיג דָּאטָה') באמצעות זיכרון מחשב מוגבל. כך המשתמשים יכולים לחלֵּץ, ברמת דיוק גבוהה, מידע רצוי, כמו למשל להעריך כמה פעמים מופיע מספר מסוים בנתונים הרבים, ללא צורך לשמור את כל המספרים. לעבודות אלה ישנן גם השלכות חשובות בתורת האינפורמציה, בתורת הגרפים, ובמגוון היבטים תיאורטיים ויישׂומיים.
המלצות למוחות צעירים
מבט על חייו של מתמטיקאי
לאנשים שאינם מתמטיקאים, קשה לדמיין איך נראים חייו של מתמטיקאי. אני זוכר שאפילו בתור סטודנט לתואר ראשון במתמטיקה, לא היה לי ברור מהי המשמעות של עריכת מחקר בתחום. כדי להעניק לכם חלון הצצה לחייהם של מתמטיקאים, אתחיל בדברים השגרתיים יותר. בתור מתמטיקאי או מתמטיקאית באוניברסיטה, יש למלא כל מיני חובות ודרישות: ללמד קורסים; להנחות סטודנטים; לכתוב מאמרים ולפרסמם. לפעמים מתקבלת בקשה לכתוב מכתב המלצה לעמית או עמיתה לתחום, או לסקור מאמר של מתמטיקאית או מתמטיקאי אחרים העוסק בתחומים שיש לך הבנה בהם. כשאני מגיע למשרד בבוקר, אני פותח את המחשב וקורא הודעות דואר אלקטרוני. לעיתים קרובות אמצא שָׁם שאלות מתמטיות שאנשים מחפשים תשובות עליהן, וסבורים שֶׁאוּכַל לספֵּק אותן או להפנותם למקורות רלוונטיים. לפעמים השאלות שאני מקבל קשורות למשהו שאני כבר מכיר, או לדָבָר דומה מאוד לְמָה שאני מכיר, ואז אני יודע לענות עליהן. פעמים אחרות, מדובר במשהו שאיני מכיר אבל מעניין אותי לחשוב עליו, ואז אני חושב קצת על השאלה ורואה אם עולים לי רעיונות לפתרון.
בזמנים אחרים לאורך היום, אני חושב על בעיות מתמטיות שקשורות למחקר האישי שלי. לפעמים אני קורא מאמרים שאנשים אחרים פרסמו על אודות השאלות המתמטיות שמעניינות אותי, ולפעמים יושב וחושב בעצמי איך אפשר לפתור בעיה מסוימת שעוד לא פתרו. בניגוד לְמָה שאנשים שאינם מתמטיקאים עשויים לחשוב, חלק ניכר מהעבודה על פתרון בעיות מתמטיות אינו כולל עיסוק ישיר במשוואות ובחישובים. הדימוי הנפוץ של מתמטיקאי כאדם שמבצע חשבונות ארוכים למדי שבסופם הוא מגיע לתוצאה הנכספת, אינו מדויק. מַרְבִּית הזמן אני עסוק במציאת רעיונות לדרכים אפשריות לפתור את הבעיה, ושואל שאלות במוחי כמו 'איזה סוג של חשבון צריך לבצע במקרה הזה?' או 'מה יכול לקדֵּם אותי בהבנה של הבעיה?'. לעיתים, בסופו של התהליך הזה תהיה משוואה שאצטרך לפתור, או חשבון שאצטרך לעשות, אבל זה יהיה רק חלק קטן בתהליך, ולרוב הוא גם יהיה התוצר של התקדמות רעיונית שהתרחשה לפניו.
חשוב לציין כי במחקר מתמטי, ובמחקר מדעי בכלל, רוב הזמן חווים תסכול במובן מסוים, עקב אי-הצלחה לפתור את הבעיות שהחוקר או החוקרת מנסים לפתור. יתרה מזו, אם כן מצליחים באופן תדיר לפתור את הבעיות שעוסקים בהן, זה מעיד על כך שהחשיבה היא על דברים פשוטים מדי ולא מספיק מעניינים. חוסר ההצלחה השוטף הזה, שהוא חלק מהותי ממחקר טוב, מְלֻוֶּה הרבה פעמים במחשבות טורדניות בסגנון 'זו בטח הייתה הפעם האחרונה שהצלחתי לפתור משהו... מכאן והלאה כבר לא אצליח...'. הניסיון מוכיח שאין זה כך, וחלק מהביטחון שצוברים לאורך הדרך קשור ביכולת לא להתפתות להאמין למחשבות המטילות סָפֵק עצמי. אדגיש כי חלק מהנכונוּת שלי כמתמטיקאי להתמודד עם המאמץ שמחקר מתמטי דורש, קשור בתקווה שלהשקעה שלי יהיו פירות – שאצליח להבין משהו שלא הבנתי קודם, ולפתור בעיה שלא פתרו לפניי. למדתי ליהנות מהאתגר שבתהליך הזה, מתוך הבנה שהרגעים שאיני נהנה בהם חשובים כי הם הופכים את ההנאה שמגיעה אחריהם להיות משמעותית וּמְסַפֶּקֶת יותר. כמו כן, ברגעים שבהם אני מרגיש 'תקוע' בעבודתי, אני דואג לעשות משהו שמְשַׁנֶּה את המצב הפנימי שלי כדי להצליח להגיע לרעיון שונה וחדש. לפעמים אבחר לחשוב על בעיה מתמטית אחרת שמעסיקה אותי, ולפעמים אחליט לעשות משהו אחר לגמרי – לקרוא ספר, לראות סרט, או לעסוק בספורט. רק לעיתים הרעיון החדש יופיע בתגובה למשהו חדש ששמעתי או קראתי. במַרבית הפעמים, כשמגיע לי רעיון כזה איני יודע מה גרם לו להופיע דווקא עכשיו, ואיך זה קשור לְמָה שעשיתי קודם. למרות שאיני יודע להתחקוֹת אחר מקור הרעיונות, ניסיוני לימד אותי כי שינוי 'מצב הצבירה' הפנימי שלי תומך לא אחת בהופעתם של רעיונות חדשים.
על מתמטיקאים צעירים
ייתכן שיעניין אתכם לדעת, כי לחוקרים צעירים יש יתרון מסוים על פני חוקרים מנוסים, במובן זה שהם פחות חוששים לעסוק בבעיות קשות שאנשים רבים לפניהם לא הצליחו לפתור. בתור חוקר מנוסה, אני מכיר מגוון בעיות מתמטיות לא פתורות, ויודע להעריך את רמת הקושי שלהן. מצד אחד, סטודנטית או סטודנט צעירים בתחילת דרכם עשויים שלא להכיר את ההיסטוריה של בעיה מתמטית מסוימת, ולא לדעת להעריך עד כמה היא קשה. לעיתים, חוסר היֶּדע הזה עשוי לְשָׁרֵת אותם, ובסופו של דבר הם יצליחו לפתור בעיה חשובה שלא פתרו לפניהם. מהצד האחר, חשוב להדגיש – במיוחד למי מכם שהמתמטיקה הבית-ספרית קלה לו או לה במיוחד – אינכם יכולים לעשות הכול ולדעת הכול בעצמכם. גם אם אתם מוכשרים ואינטליגנטיים מאוד, עדיין תידָרשו ללמוד הרבה מהיֶּדע שנצבר על ידי דורות שלמים של מתמטיקאים חכמים שהשקיעו הרבה מזמנם כדי לפתֵּח שיטות שונות במתמטיקה. רכישת הידע הזו מתבצעת לרוב על ידי עיון בספרות המדעית; האזנה להרצאות, וקיום דיונים עם מתמטיקאיות ומתמטיקאים אחרים שמתעניינים באותם תחומים.
מחשבות על פרסים והישׂגים
במהלך הקריירה שלי קיבלתי פרסים רבים למדי. בכל פעם, שמחתי לִזְכּוֹת בהכרה על עבודתי, ותמיד עודד אותי להיווכח כי מה שעשיתי מעניין גם אנשים אחרים. הפרסים שקיבלתי אף היטיבו עם הקריירה שלי, ואִפשרו לי גמישוּת בבחירות האקדמיות שלי לאורך הדרך. לצד זה שאני נהנה לקבל פרסים, חשוב לי להדגיש שאיני מכוון את מחקרי למטרה זו. סיבה מרכזית לכך היא שפרסים אינם דבר מובטח, והם תלויים במגוון גורמים שאין לי שליטה עליהם. במקרים רבים, אין לי אפשרות לדעת איזו חשיבוּת יש לדברים שאני עושה, וזו מתגלה רק בדיעבד. דוגמה טובה לכך היא למשל המחקר שסיפרתי לכם עליו קודם בנושא התכונות של מידע זורם, שבדיעבד התברר כחשוב, וּפָתַח תחום מתמטי חדש שנקרא 'אלגוריתמֵי הַזְרָמָה' (streaming algorithms). במחקר שלי, אני תמיד משתדל שהקריטריון העיקרי יהיה לעשות מה שהכי מעניין אותי. מאחר שפעמים רבות ההשפעה של מה שאני חוקר מתגלה בדיעבד והיא בלתי צפויה, חשוב בעיניי לעשות עכשיו את הדברים שמעניינים אותי בהווה. זה מחבּר אותי להמלצה כללית יותר שאני מבקש להעניק לכם, והיא: עִסְקוּ בַּמֶּה שאתם אוהבים, וְאֶהֱבוּ את מה שאתם עושים. אלה שני צדדים של אותו המטבּע, ושניהם חשובים. בִּמקום לעשות עכשיו משהו שלא כל כך מעניין אתכם מתוך מחשבה שבהמשך הוא יוביל אתכם להצלחה, בַּחֲרוּ לעשות כבר עכשיו את מה שאתם אוהבים לעשות. לפעמים זה יוביל אתכם להצלחה ולפעמים אולי לא, אך בכל מקרה באופן זה תבלוּ את חייכם בעשייה שתהיה משמעותית עבורכם.
מילון מונחים
אובייקטיבי (Objective): ↑ משהו שלא מושפע מדעה אישית, ואי אפשר להתווכח עליו.
סוציולוג (Sociologist): ↑ אדם החוקר את החברה - קבוצות ויחידים בתוכה, וגם היא כשלעצמה.
קומבינטוריקה (Combinatorics): ↑ תחום במתמטיקה העוסק בחקירת התכונות של קבוצות סופיות של עצמים.
טופולוגיה (Topology): ↑ ענף במתמטיקה העוסק בתכונות של המרחב הנשמרות גם אחרי שינויים רציפים במרחב.
תורת המשחקים האלגוריתמית (Algorithmic game theory): ↑ תורה מדעית שמשלבת בין תורת המשחקים, שחוקרת אינטרקאציות ביו גורמים בעלי אינטרסים שונים, לבין תורת החישוביות, שעוסקת במודלים של חישוב ובאלגוריתמים לביצוע פעולות חישוביות.
תורת האינפורמציה (Information theory): ↑ ענף במתמטיקה שבמסגרתו נחקרת העברת מידע בין מקור ליעד המחוברים על ידי ערוץ תקשורת.
תורת הגרפים (Graph theory): ↑ תחום במתמטיקה שעוסק בגרפים - מבנים קומבינטוריים המופיעים בהקשרים רבים.
הצהרת ניגוד אינטרסים
המחברים מצהירים כל המחקר נערך בהעדר כי קשר מסחרי או פיננסי שיכול להתפרש כניגוד אינטרסים פוטנציאלי.
תודות
אני רוצה להודות לנועה שגב על עריכת הריאיון שהיווה בסיס למאמר זה, ועל כתיבה משותפת של המאמר. תודה לאלכס ברנשטיין על האיורים עבור המאמר.
מקורות
[1] ↑ Van Lint, J. H., and Wilson, R. M. (2001). A course in combinatorics. Cambridge university press.
[2] ↑ Alon, N. (1987). Splitting necklaces. Adv. Math. 63(3), 247-253.
[3] ↑ Alon, N., Matias, Y., and Szegedy, M. (1999). The space complexity of approximating the frequency moments. J. Comput. Syst. Sci. 58(1), 137-147.
