תַקצִיר
מגפת הקורונה, המכונה גם קוֹבִיד-19, הובילה לשינויים משמעותיים באופן שבו אנשים חיים את חייהם כיום. במטרה לקבוע מהי הדרך המיטבית להפחית את השפעות המַגֵּפָה ולהתחיל לפתוח מחדש את השירותים השונים לציבור, ממשלות השתמשו במודלים מתמטיים של התפשטות מחלות מידבקות. במאמר זה, נכיר את הסוג השכיח של מודל מתמטי להתפשטות מחלות. נדון גם באופן שבו תוצאות ניתוח מודלים מתמטיים יכולות להשפיע על מדיניוּיוֹת ממשלתיות ועל התנהגות אנושית, כמו למשל עידוד חבישת מַסֵּכַת פָּנִים ושמירה על ריחוק פיזי כדי לסייע בהאטת התפשטות המחלה.
מִדּוּל מחלות זיהוּמיוֹת
בסוף שנת 2019, רופאים ומדענים למדו התוודעו לנגיף חדש שנקרא ’נגיף קורונה של תסמונת נשימתית חמוּרה מספר 2’ (באנגלית ‘Severe Acute Respiratory Syndrome coronavirus 2’) או בקיצור סַארְס-קוֹב-2 (SARS-CoV-2), שהתפשט בסין. הנגיף גרם למחלה בשם ’מחלת נגיף קורונה 2019’, או בשמה הנוסף קוֹבִיד-19 (COVID-19, ראשי תיבות של Coronavirus disease 2019) [2 ,1] שהתפשטה ברחבי העולם כמַגֵּפָה1 עולמית. מה שגורם לנגיף הזה להיות מסוכן כל כך היא העובדה שהוא מתפשט בקלות רבה בין אדם לאדם, ואנשים שנדבקים בו עלולים לחלות במחלה קשה ואף למות.
מדענים מסייעים לאנשים להחלים מנגיפים באמצעות תכנון תרופות וציוד רפואי. בעזרת שימוש במתמטיקה ובחישובים, מדענים גם חוקרים דרכים לשמור על אנשים מוגנים על ידי חקירת ההשפעות של פעולות כמו שמירה על ריחוק פיזי וחבישת מסכות. ממשלות יכולות להשתמש ביֶדַע שנרכש ממחקר כזה כדי לפתח הנחיות ומדיניוּיוֹת בתחום הבריאוּת. במאמר זה, נדון במידול מתמטי של מחלות זיהומיות [6 ,5]. מדענים שמתמחים במחקרים כאלה לעיתים קרובות נקראים אֶפִּידֶמְיוֹלוֹגִים מתמטיים.
כדi לשפר את הבנתנו לגבי האופן שבו מחלות מתפשטות, מדענים משתמשים בשילוב של מתמטיקה ונתונים עבור מידול מתמטי. מודלים מתמטיים מספּקים דרך לנסח חוקים פשוטים במטרה להעריך כיצד נגיף כמו סַארְס-קוֹב-2 מתפשט, ובכך להעריך את התפשטות המחלה המקושרת לנגיף – מחלת נגיף קורונה 2019. כאשר יוצרים מודל מתמטי וחוקרים אותו, מדענים מבקשים לשפר את דיוק התחזיותלגבי האופן שבו המחלה תתפשט. הם גם מנסים לבחון את ההשפעות של תגובות אפשריות, כמו למשל הנחיה שלפיה כולם נדרשים להישאר בבתים, במטרה להפחית את מספר ההדבקות שנובעות מהתפשטות המחלה. מחקר מסוג זה יכול לסייע ליידע את הגורמים המגבשים את ההנחיות או המדיניות שמטרתן להגן על אנשים אחרים מפני מחלות [5].
דרך אחת לְמַדֵּל מתמטית כיצד מחלה מתפשטת היא להשתמש במודל תָּאִי, כמו למשל מודל SIR (ראו איור 1). במודל תאי, מדענים מפרידים את האוכלוסייה לקטגוריות שנקראות ’תאים’, ובוחנים כיצד אנשים נעים בין הקטגוריות במשך הזמן. שמו של מודל מסוג SIR הוא ראשי תיבות של סוגי התאים שהוא מכיל: ’רגישים’ (susceptible), ’נדבקו’ (infected) ו’החלימו’ (recovered). תא ה-’S’ מכיל אנשים שהם רגישים, או מועדים, לזיהום, כלומר עלולים להידבק במחלה המתפשטת. תא ה-’I’ מכיל אנשים שנדבקו במחלה, ולכן עלולים להדביק אחרים. תא ה-’R’ מכיל אנשים שהחלימו מהמחלה, אף על פי ש-’R’ יכול לסמן גם ’removed’ (הוסרו), כדי להביא בחשבון אנשים שנפטרו עקב הידבקות במחלה.

- איור 1 - מודל תאי – אחת הדרכים למידול מתמטי של התפשטות מחלה זיהומית.
- במודל תאי מסוג SIR, מחלקים את האוכלוסייה לתאים של אנשים רגישים (S), אנשים שנדבקו (I) ואנשים שהחלימו (R). משמאל למעלה עם כיוון השעון: ביום הראשון – התחילו עם אדם אחד שנדבק, אשר מפיץ את המחלה לשני חברים; ביום השני – חברים אלה נדבקים במחלה, וכל אחד מהם מפיץ את המחלה לחבריו האחרים – מוביל לשלושה אנשים נוספים סך הכול; ביום השלישי – אם כל מי שחולה נשאר בבית, אז אף אחד אחר לא נדבק (וחלק מהאנשים נשארים רגישים); ביום הרביעי – בסופו של דבר, כל האנשים שנדבקו יהיו בתא של ’החלימו’ (recovered) או ’הוסרו’ (removed).
כאשר מפתחים מודל מתמטי של התפשטות מחלה, רצוי להתמקד בגורמים החשובים ביותר עבור התפשטותה, ובשאלות המדעיות המסוימות שמעניינות אותנו, כך שהמודל יהיה פשוט ואינפורמטיבי ככל הניתן. גורמים אלה שונים עבור מחלות שונות. גורמים רלוונטיים כוללים את תדירותם של מגעים אישיים וּמִשְׁכָם, כמו למשל לחיצת ידיים, צפייה יחד בסרט, או משחק במשחקי קופסה [6]. מגעים כאלה מַקְנִים למחלה הזדמנות להתפשט. חלק מסוגי המחלה דורשים מגע קרוב מאוד כדי להתפשט, אך סוגים אחרים יכולים להתפשט אפילו רק על ידי נגיעה באותו המשטח שבו נגע אדם שנדבק, או שהייה בלבד במחיצתו של אדם כזה.
כמה מהר מחלה מתפשטת?
נדגים את המידול של התפשטות מחלה זיהומית באמצעות מודל SIR [5]. לפני שנוכל להשתמש במודל זה כדי לחקור התפשטות מחלה באוכלוסייה, עלינו לדעת (או להעריך) כמה גורמים חשובים:
- מֶשֶׁך הזמן שבו אדם מידבק – זה יאמר לנו כמה זמן אנשים שנדבקו יכולים להדביק אנשים אחרים.
- קצב המגע האישי באוכלוסייה – מַדָּד זה מצביע על התדירות שבה אנשים נמצאים קרובים מספיק זה לזה כך שהמחלה תתפשט מאדם לאדם.
- הסיכוי שמגע אישי יוביל להדבקה.
שלושת הגורמים האלה מאפשרים למדענים להעריך מַדָּד שנקרא מספר ההתרבּוּּת הבסיסי, אשר מסומן על ידי R0 (מבוטא באנגלית ’אַר נוֹט’, R naught). הערך של R0 מצביע על המספר הממוצע של אנשים אשר להם אדם מידבק אחד מפיץ את המחלה, באוכלוסייה של אנשים רגישים. נניח שמחלה מתפשטת בעיר לוס אנג’לס בארצות הברית. לפני תחילת התפשטות המחלה, כל האנשים בלוס אנג’לס נכללים בתא ה’רגישים’. כעת, נניח שמישהו חולה טס ללוס אנג’לס ומתחיל להפיץ את המחלה לאנשיםבעיר. אם R0 הוא 2 והזמן שבו האדם מידבק הוא יום 1 (ואז הוא או היא מחלימים), אותו האדם יפיץ את המחלה לשני אנשים אחרים, בממוצע, לפני שיחלים. שני האנשים האלה, בתורם, יפיצו את המחלה לשני אנשים נוספים בממוצע לפני שכל אחד מהם יחלים, וכך הלאה. במסגרת הפשוטה הזו, אנו יכולים להעריך כמה אנשים יידבקו בתוך זמן מסוים.
כאשר R0 גדול יותר מ-1 (נכתב מתמטית כ-R0 > 1”), מספר האנשים שנדבקים גָּדֵל באופן אקספוננציאלי. כדי להדגים כיצד גדילה אֶקְסְפּוֹנֶנְצְיָאלִית (מַעֲרִיכִית) פועלת, נשתמש בדוגמה שלנו לעיל, עם R0 = 2 ותקופת זיהום של יום 1. נניח שהאדם שנדבק בהתחלה מדביק שני אנשים ביום שבו הוא או היא טסים ללוס אנג’לס, ושכל אחד משני האנשים האלה מדביק שני אנשים נוספים למוחרת (זִכְרוּ כי בדוגמה הזו אדם שנדבק מחלים תוך יום 1אחד). ביום שלמוחרת, כל אחד מארבעת האנשים שנדבקו יכול להדביק שני אנשים רגישים נוספים. ביום השלישי, אנו מצפים שיהיו לנו כ-2 × 2 = 8 × 2 אנשים שנדבקו. אם הדפוס הזה ממשיך ועדיין ישנם אנשים רגישים רבים, נכפיל שוב פי 2 וּנְצַפֶּה שיהיו 16 אנשים חדשים שנדבקו ביום הבא. זכרו כי הדבקות אלה מגיעות מאדם אחד בלבד שנדבק בהתחלה! אם במקום זאת נתחיל מ-100 אנשים שנדבקו, נוכל לראות כיצד המצב עלול להידרדר מהר מאוד ולהיות גרוע מאוד.
מספר האנשים שנדבקים במחלה ממשיך לגדול עד שהשיעור שבו אנשים שנדבקו מחלימים, עולה על השיעור שבו הם מדביקים אנשים רגישים. אם כל אדם שנדבק מדביק פחות מאשר אדם אחד ליום בממוצע, אנו מצפים שיהיו פחות הדבקות בכל יום, ושהמחלה תדעך בסופו של דבר. כמה זמן זה לוקח, ואם זה קורה, תלוי בגודל האוכלוסייה ובמגע האישי בין האנשים הנמנים עימה2.
באיור 2, אנו משווים מה קורה למספרים של שלוש הקטגוריות באוכלוסייה: אנשים רגישים; אנשים שנדבקו ואנשים שהחלימו, כאשר R0 > 1 לעומת R0 < 1. באיור 2A (שעבורו R0 > 1), מספר האנשים שנדבקו באותו הזמן יכול להיות גדול מאוד (ראו עקומה כתומה), ובתי החולים עשויים שלא להיות מסוגלים לטפל בכל האנשים שנדבקים. כאשר R0 < 1 (ראו איור 2B), המחלה אינה מתפשטת לאנשים רבים באוכלוסייה, ולכן העקומה של אנשים שנדבקו משתטחת עם הזמן. זהו התרחיש הרצוי, ואם המחלה מתפשטת במהירות, אנו מעוניינים להאט את קצב ההדבּקות וּ’לְשַׁטֵּחַ את העקומה’3 (ראו איור 3).
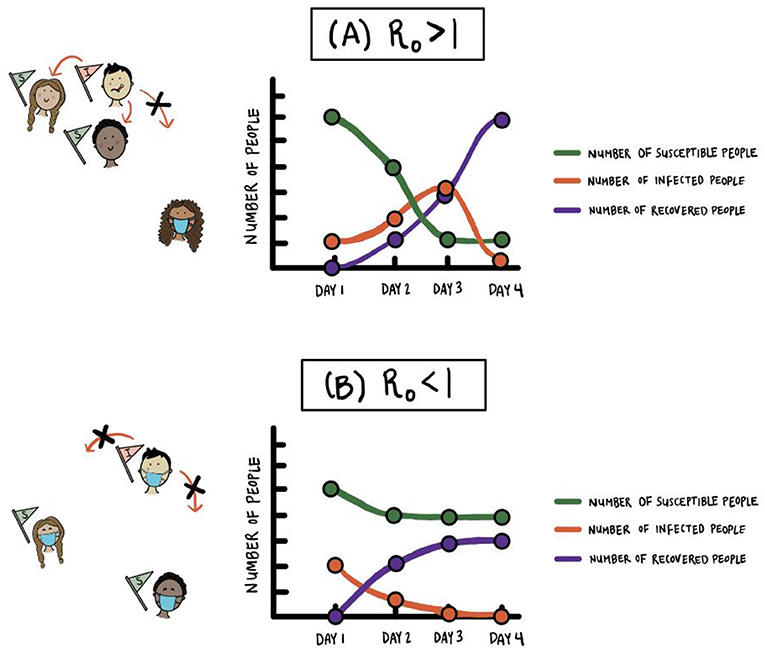
- איור 2 - השוואה בין קטגוריות אנשים במסגרת מודל SIR.
- השוואה של מספר האנשים הרגישים (susceptible people); האנשים שנדבקו (infected people והאנשים שהחלימו (recovered people) במודל SIR של מחלה זיהומית. הערכים בציר האנכי מצביעים על סך כל האנשים בתאים אלה: האנשים הרגישים; האנשים שנדבקו והאנשים שהחלימו בכל יום (לא רק על ההדבקות וההחלמות החדשות לאותו היום). (A) כאשר R0 > 1, מספר האנשים שנדבקים באותו הזמן יכול להיות גדול מאוד, ובתי החולים עלולים שלא להיות מסוגלים לטפל בכולם. מאחר שבמצב זה כמעט כולם נדבקים לאורך הזמן, מספר האנשים הרגישים בסופו של דבר קָטֵן מאוד. (B) כאשר R0 < 1, למשל כשהרבּה אנשים חובשים מסכות ושומרים על ריחוק פיזי, המחלה אינה מתפשטת בקרב אנשים רבּים באוכלוסייה.
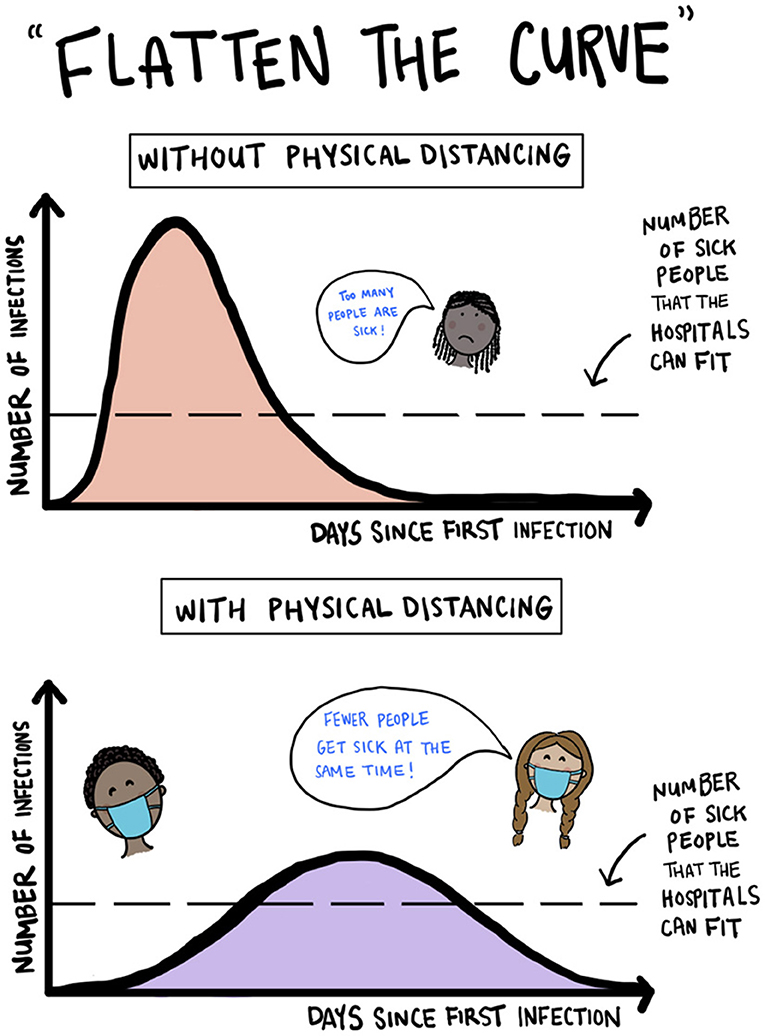
- איור 3 - הַמְחָשַׁת ’שיטוח העקומה’ של זיהום באמצעות שמירה על ריחוק פיזי.
- חלק עליון: ללא ריחוק פיזי; חלק תחתון: עם ריחוק פיזי (האיור שלנו בהשראת תמונות כמו זו שב: https://commons.wikimedia.org/wiki/File:Covid-19-curves-graphic-social-v3.gif, אשר אוירה על ידי Siouxsie Wiles ו-Toby Morris).
’שיטוח העקומה’, מדיניות והתנהגויות
במחשבה על האופן שבו מחלה מתפשטת, רשתות של מגעים אישיים חשובות להערכת ערכּוֹ של R0 [6 ,4]. אתם וחבריכם מחוברים זה לזה ברשת חברתית פיזית, וכך גם הוריכם וחבריהם. לכן, אם אחד מחבריכם חולה, המחלה עלולה להתפשט אליכם ואז להוריכם ומהם לחברים שלהם. אנשים שנדבקו, אשר פוגשים חברים רבים שלהם באופן אישי, עלולים להפיץ את המחלה לאנשים רבים נוספים.
בְּשֶׁל הקלוּת שבה אנשים עלולים להידבק בנגיף סארס-קוב-2, ואולי לחלות מאוד במחלת נגיף קורונה 2019, ממשלות רבות הגיבו למגפת הקורונה בשׁורה של צעדים ופעולות. עם אלה נמנים סגירת בתי ספר; ביטול אירועי ספורט והתאגדויות גדולות אחרות; הַכְנָסַת אנשים שנדבקו לבידוד, והוראה לאנשים להישאר בבתים ולשמור על ריחוק פיזי. מטרת סוגי המדיניויות וההתנהגויות האלה במהלך מגפה היא לנסות להגביל מגעים אישיים ישירים ועקיפים, ובכך ’לשטח את העקומה’ של מספר האנשים הנדבקים (ראו ( [6 ,4 ,3]. בעזרת אמצעים כאלה, לצד הקפדה על חבישת מסכות ושטיפת ידיים לעיתים תכופות, מספר האנשים שנדבקים משׂתרע על פני זמן ממושך יותר, והשיא שלו נמוך יותר. זה מצביע על כך שהמספר הַמְּרַבִּי של אנשים שנדבקו בכל יום קטן יותר ממה שהיה יכול להיות אחרת. הדבר חשוב כדי שלבתי חולים תהיה יכולת לטפל בכמה שיותר אנשים שניתן. עם עקומה משוטחת, אף על פי שמחלה ממשיכה להתפשט, קצב התפשטותה איטי יותר, ולכן יש יותר מקום בבתי חולים לטפל באנשים שנדבקו וזקוקים לסיוע. מצב דברים זה מפחית את מספר המיתוֹת כתוצאה מהמחלה. שיטוח העקומה גם מפחית את מספר האנשים הכולל שנדבקים לאורך הזמן.
מסקנות
מודלים מתמטיים וחישוביוּת מילאו תפקיד מרכזי בהשפעה על תגובות של ממשלות למגפת הקורונה. הקורונה. מודלים אלה מפורטים הרבה יותר ממודל SIR שדנו בו לעיל4. לדוגמה, מודלים רבים כללו תא עבור אנשים ללא תסמינים שעדיין עלולים להדביק אנשים אחרים, ומודלים מסוימים כללו תא עבור אנשים שאושפזו בבתי החולים.
מגפת נגיף קורונה 2019 ממחישה את חשיבות המידול המתמטי של מחלות זיהומיות. גישות מתמטיות וחישוביוֹת מאפשרות לאנשים להתקדם לקראת הפחתת התפשטות מחלה, בזמן שחוקרים מפתחים חיסונים נגד המחלה וטיפולים בה. גישות אלה גם מסייעות למאמצים לְעַצֵּב התערבוּיוֹת ותוכניות התחסנות.
מילון מונחים
מגפה (Pandemic): ↑ ההופעה השכיחה של מחלה זיהומית בכמה יבשות, או אפילו ברחבי העולם.
מידול מתמטי (Mathematical Modeling): ↑ מודל מתמטי הוא תיאור מפושט של משהו באמצעות חוקים מתמטיים ושפה מתמטית. פיתוח מודל כזה, בדיקתו וליטושו, ידועים בתור מידול מתמטי. דוגמה למודל כזה הוא מודל SIR של התפשטות מחלות מידבקות.
אפידמיולוג מתמטי (Mathematical Epidemiologist): ↑ מדען שחוקר מחלות זיהומיות באמצעות מידול מתמטי וחישוביוּת.
תחזית (Forecast): ↑ סוג של חיזוי שמספק טווח אפשרויות עבור תוצאות עתידיות. לדוגמה, חזאי או חזאית מזג אוויר יכולים לומר בחדשות שקיים סיכוי של %42 לגשם בלוס אנג’לס מחר. מדען או מדענית עשויים לחזות טווח עבור מספר האנשים בלוס אנג’לס שֶׁיֶּחֱלוּ במחלת הקורונה במהלך חודש מסוים.
מודל תאי (Compartmental Model): ↑ סוג המודל המתמטי השכיח ביותר שחוקרים משתמשים בו כדי לחזות כיצד מחלה מתפשטת. מודל תאי של התפשטות מחלה זיהומית מכיל קטגוריות שונות שנקראות ’תאים’, כמו למשל ’נדבקו’ ו’החלימו’, וכן חוקים מתמטיים עבור האופן שבו אנשים עוברים בין תא אחד לאחר. לדוגמה, באמצעות מודל (SIR susceptible–infected–recovered, ובעברית: רגישים-נדבקים-מחלימים), אנו יכולים לחקור כיצד מספריהם באוכלוסייה של אנשים רגישים למחלה, אנשים שנדבקו ואנשים שהחלימו משתנים עם הזמן.
מגע (Contact): ↑ אינטראקציה מכל סוג בין שני פרטים. מגע אישי יכול להיות ישיר, כמו למשל לחיצת ידיים, או עקיף, כמו למשל נגיעה באותו המשטח או הימצאות בקרבתו של האחר.
מספר ההתרבות הבסיסי [Basic Reproduction Number (R0)]: ↑ מספרן הממוצע של ההדבקות המיוצרות על ידי אדם אחד שנדבק בקרב אוכלוסיית אנשים הרגישים למחלה.
גדילה אקספוננציאלית (Exponential Growth): ↑ סוג גדילה מהיר במיוחד. כאשר מחלה גְּדֵלָה באופן אקספוננציאלי, מספר האנשים שנדבקים גָּדֵל באופן פרופורציונלי למספר העדכני של האנשים שנדבקו. לדוגמה, אם אדם אחד נדבק ביום הראשון שבו המחלה מדביקה מישהו באוכלוסייה, וכמות האנשים שנדבקים באוכלוסייה גדלה פי שלושה בכל יומיים, אז ביום השלישי יהיו שלושה אנשים שנדבקו, ביום החמישי תשעה אנשים שנדבקו, ביום השביעי 27 אנשים שנדבקו, ביום התשיעי 81 אנשים שנדבקו, וכן הלאה.
הצהרת ניגוד אינטרסים
המחברים מצהירים כי המחקר נערך בהעדר כל קשר מסחרי או פיננסי שיכול להתפרש כניגוד אינטרסים פוטנציאלי.
תודות
אנו מודים לקוראים הצעירים שלנו – Emily Chen, Nia Chiou, Taryn Chiou, Dimitri Chrysafis, Maria Chrysafis, Valerie K. Eng, Iris Leung, Talan Li, Adam Lindemood, Suzanna Lindemood ו- Eli Truong – עבור הערותיהם המועילות הרבות. אנו מודים גם להוריהם, למוריהם ולחבריהם – Alena Carter, Lyndie Chiou ו- Christina Chow– על שקישרו אותנו אליהם ועודדו את המשוב שלהם. אנו מודים ל-John Butler, Francesca Henderson, Rachel Levy, Joel Miller, לעורכים שלנו ולסוקרים שלנו על הערותיהם המועילות. MAP מודה על התמיכה מהקרן הלאומית למדע (מענק מספר DMS-2027438) דרך תוכנית RAPID; MAPו-YHK מודים על התמיכה מהקרן הלאומית למדע (מענק מספר (1922952 דרך תוכנית האלגוריתמים לאיתור אִיּוּם (ATD).
הערות שוליים
1. ↑ ראו Zaman [3] כדי ללמוד עוד על מגפות, ו-Alberca ואחרים [1] ו- [4] עבור הקדמה נגישׁה למגפת הקורונה, קוֹבִיד-19.
2. ↑ נַסּוּ את המודל האינטראקטיבי SIR ב-Edenharter [7]. תוכלו גם לעיין בדיונים ב-Weinersmith ואחרים [6] וב-Zaman [3], ובדיונים ובסימולציות האינטראקטיביות ב-Salatheé ו-Case [4].
3. ↑ כעת, מִשֶּׁדָּנוּ מעט יותר ב-R0, הִתְבּוֹנְנוּ שוב במה קורה כאשר אתם משנים נתונים כמו שיעורי הדבקה ושיעורי החלמה בסימולציה האינטראקטיבית, ב-Edenharter [7].
4. ↑ ראו Ferguson ואחרים [8] לפרטים לגבי המודל שהיה בשימוש בבריטניה.
מקורות
[1] ↑ Alberca, G. G. F., Fernandes, I. G., Sato, M. N., and Alberca, R. W. 2020. What is COVID-19? Front Young Minds 8:74. doi: 10.3389/frym.2020.00074
[2] ↑ World Health Organization. 2020. Coronavirus Disease (COVID-19) Pandemic. Available online at: https://www.who.int/emergencies/diseases/novel-coronavirus-2019.
[3] ↑ Zaman, L. 2020. Developing an Intuition for Pandemics. Available online at: https://infectiousmatter.com
[4] ↑ Salathé, M., and Case, N. 2020. What Happens Next? COVID-19 Futures, Explained With Playable Simulations. Available online at: https://ncase.me/covid-19/?v=3
[5] ↑ Brauer, F., Castillo-Chavez, C., and Feng, Z. 2019. Mathematical Models in Epidemiology. Heidelberg, Germany: Springer-Verlag.
[6] ↑ Weinersmith, Z., Koerth, M., Bronner, L., and Mithani, J. 2020. A Comic Strip Tour of the Wild World of Pandemic Modeling. Available online at: https://fivethirtyeight.com/features/a-comic-strip-tour-of-the-wild-world-of-pandemic-modeling/
[7] ↑ Edenharter, G. 2015. The Classic SIR Model. Available online at: https://maple.cloud/app/4837052487041024
[8] ↑ Ferguson, N. M., Laydon, D., Nedjati-Gilani, G., Imai, N., Ainslie, K., Baguelin, M., et al. 2020. Report 9: Impact of Non-pharmaceutical Interventions (NPIs) to Reduce COVID-19 Mortality and Healthcare Demand. Available online at: https://www.imperial.ac.uk/mrc-global-infectious-disease-analysis/covid-19/report-9-impact-of-npis-on-covid-19/
