ملخص
أدخلت جائحة كوفيد-19 تغييرات جوهرية على الطريقة التي يعيش بها الناس حياتهم حاليًا. ولتحديد أفضل السبل اللازمة للحد من تأثيرات الجائحة والبدء في إعادة فتح المجتمعات، استخدمت الحكومات نماذج رياضية تتنبأ بانتشار الأمراض المعدية. وفي هذا المقال، نطرح نوعًا شائعًا من النماذج الرياضية الخاصة بانتشار المرض. حيث نناقش كيف يمكن لنتائج تحليل النماذج الرياضية التأثير على سياسات الحكومات والسلوك البشري؛ مثل التشجيع على ارتداء الكمامات والتباعد الجسدي الاجتماعي من أجل المساعدة في إبطاء انتشار مرض ما.
نمذجة الأمراض المعدية
في ختام عام 2019، تعرَّف الأطباء والعلماء على فيروس مستجد، يُطلق عليه الآن ”المتلازمة التنفسية الحادة الشديدة الناتجة عن فيروس كورونا 2” (فيروس ”سارس-كوف-2” (SARS-CoV-2))، الذي كان متفشيًا في الصين. تسبب الفيروس في الإصابة بمرض يُطلق عليه ”مرض فيروس كورونا 2019” (أي كوفيد-19) [1, 2] الذي انتشر في جميع أنحاء العالم باعتباره جائحة1 عالمية. إن ما يجعل هذا الفيروس خطيرًا للغاية هو قدرته على الانتقال بمنتهى السهولة من شخص إلى آخر، وأن الأشخاص المصابين بكوفيد-19 قد يمرضون بشدة ويفارقون الحياة.
يساعد العلماء الأشخاص في التعافي من الفيروسات عن طريق تصميم أدوية ومعدات طبية. وباستخدام الرياضيات والحوسبة، يبحث العلماء أيضًا عن طرق للحفاظ على سلامة الناس من خلال دراسة تأثيرات تدابير احترازية؛ مثل التباعد الجسدي وارتداء الكمامات. يمكن للحكومات بعد ذلك استخدام المعرفة المكتسبة من مثل هذه الأبحاث في وضع مبادئ توجيهية وسياسات صحية لمواجهة الأزمة. نناقش في هذا المقال النمذجة الرياضية للأمراض المعدية [5, 6]. وعادة ما يُطلق على العلماء المتخصصين في هذه الدراسات ”اختصاصيي النمذجة الرياضية للأوبئة”.
لتحسين فهمنا لطريقة انتشار مرض ما، يستخدم العلماء مزيجًا من الرياضيات والبيانات لتطبيق النمذجة الرياضية. توفر النماذج الرياضية طريقة لصياغة القواعد البسيطة لتقديم تخمين تقريبي لكيفية انتشار فيروس، مثل فيروس ”سارس-كوف-2”؛ وبالتالي تقديم تخمين تقريبي لانتشار مرض كوفيد-19 المصاحب للفيروس. عند إنشاء ودراسة أحد النماذج الرياضية، يسعى العلماء إلى تحسين دقة التنبؤات المتعلقة بطريقة انتشار مرض ما. كما يحاولون أيضًا اختبار تأثيرات الاستجابات المحتملة، مثل ملازمة جميع الناس منازلهم، لتقليل عدد الإصابات الناتجة عن انتشار مرض ما. يمكن أن تساعد أبحاثهم في إرشاد الأشخاص الذين يضعون مبادئ توجيهية أو سياسات لحماية الآخرين من الأمراض [5].
تتمثل إحدى طرق النمذجة الرياضية لكيفية انتشار مرض ما في استخدام نموذج مجزأ، مثل نموذج SIR (انظر الشكل 1). يقوم العلماء في النموذج المجزأ، بتقسيم السكان إلى فئات يُطلق عليها ”أقسام” وفحص كيف يغير الناس فئاتهم بمرور الوقت. تستمد نماذج SIR تسميتها من أقسامها، وهي كالآتي: قسم الأشخاص ”المعرضين للإصابة” (S)، وقسم ”المصابين” (I)، وقسم ”المتعافين” (R). يتألف القسم S من الأشخاص المعرضين للإصابة بالعدوى، مما يعني أنهم قد يُصابوا بالمرض الآخذ في الانتشار. ويتألف القسم I من الأشخاص المصابين، والذين ينقلون بدورهم العدوى إلى الآخرين. يتكون القسم R من الأشخاص الذين تعافوا من المرض، على الرغم من أن القسم R قد يشير أيضًا إلى ”المستبعدين من الإصابة” تمثيلًا للأشخاص الذين تُوفوا بسبب المرض.

- شكل 1 - تتمثل إحدى طرق النمذجة الرياضية لكيفية انتشار مرض معد في استخدام نموذج مجزأ.
- في أحد أنواع النماذج الرياضية المُسمى نموذج ،SIR تُقسم أي مجموعة سكانية إلى عدة أقسام: الأشخاص المعرضون للإصابة (S)، والأشخاص المصابون (I)، والأشخاص المتعافون (R).
عند إعداد نموذج رياضي لانتشار مرض ما، من المستحسن التركيز على العوامل الأكثر أهمية لانتشار هذا المرض، وعلى التساؤلات العلمية المعينة ذات الأهمية، بحيث يكون النموذج بسيطًا ومفيدًا قدر الإمكان. تختلف العوامل باختلاف الأمراض. وتشمل العوامل ذات الصلة معدل تكرار المخالطات الشخصية ومدتها؛ مثل المصافحة أو مشاهدة فيلم معًا أو ممارسة ألعاب الطاولة [6]. تعطي هذه المخالطات فرصة للمرض كي ينتشر. يتطلب انتشار بعض أنواع الأمراض مخالطة لصيقة للغاية، ولكن البعض الآخر قد ينتشر بطرق بسيطة؛ عن طريق لمس السطح نفسه الذي لمسه المصاب أو مجرد التواجد في مكان قريب على سبيل المثال.
ما مدى سرعة انتشار مرض ما؟
لنوضح نمذجة انتشار مرض معد باستخدام نموذج SIR [5]، قبل أن نستخدم نموذج SIR لدراسة انتشار مرض ما في مجموعة سكانية، يجب علينا معرفة (أو تقدير) بضعة عوامل مهمة:
- مقدار الوقت الذي يكون خلاله الشخص ناقلًا للعدوى. وهذا يخبرنا بالمدة التي يمكن خلالها للأشخاص المصابين نقل العدوى إلى أشخاص آخرين.
- معدل المخالطة الشخصية في مجموعة سكانية. وهذا يشير إلى عدد المرات التي يكون فيها الناس على مقربة من بعضهم بعضًا بدرجة تكفي لانتشار المرض من شخص لآخر.
- احتمال أن تؤدي المخالطة الشخصية إلى انتقال عدوى.
تسمح تلك العوامل الثلاثة للعلماء بتقدير كمية يطلق عليها عدد التكاثر الأساسي، والذي يُشار له بالرمز R0 ،(وينطق ”R naught”). تشير قيمة R0 إلى متوسط عدد الأشخاص الذين ينقل إليهم شخص مصاب واحد مرض ما ضمن مجموعة من الأشخاص المعرضين للإصابة به. افترض أن مرضًا ما ينتشر في مدينة لوس أنجلوس. قبل بدء المرض في الانتشار، يعتبر كل فرد في لوس أنجلوس ضمن قسم ”المعرضين للإصابة”.
الآن افترض أن الشخص الحامل للمرض يسافر إلى لوس أنجلوس ويبدأ في نقل العدوى للآخرين. إذا كانت قيمة R0 تساوي 2 وكانت الفترة التي يكون خلالها الشخص ناقلًا للعدوى تساوي يومًا واحدًا (ويتعافى بعد ذلك)، فسينقل هذا الشخص المرض إلى شخصين آخرين، في المتوسط، قبل أن يتعافى. وبالتالي سوف ينقل هذان الشخصان المرض إلى شخصين آخرين في المتوسط قبل التعافي، وهكذا دواليك. في هذا الطرح المبسط، يمكننا تقدير عدد الأشخاص الذين سوف يصبحون مصابين خلال فترة معينة.
إذا كانت قيمة R0 أكبر من 1 (والتي نعبر عنها رياضيًا بـ ” R0 > 1”)، فسيزداد عدد الأشخاص المصابين باطراد. لمعرفة كيفية عمل النمو الأسي، نستخدم المثال أعلاه R0 = 2 وفترة نقل عدوى مدتها يوم واحد. افترض أن أول شخص مصاب بالعدوى ينقل العدوى إلى شخصين في اليوم الذي يسافر فيه إلى لوس أنجلوس وينقل كل شخص من هذين الشخصين العدوى إلى شخصين آخرين في اليوم التالي. وتذكر أن الشخص المصاب سيتعافى في غضون يوم واحد في هذا المثال. وفي اليوم الذي يلي ذلك، يمكن أن يصيب كل شخص من هؤلاء الأشخاص الأربعة المصابين شخصين آخرين معرضين للإصابة. وفي غضون ثلاثة أيام، نتوقع أن يكون لدينا حوالي 2 ×2 ×2 = 8 أشخاص مصابين. إذا استمر هذا النمط ولا يزال هناك العديد من الأشخاص المعرضين للإصابة، فإننا نضرب العدد في 2 مرة أخرى، لذلك نتوقع أن يكون لدينا حوالي 16 شخصًا مصابًا حديثًا في اليوم التالي. تذكر أن حالات العدوى تلك تنتقل من شخص مصاب واحد في البداية! لكن إذا بدأنا بـ 100 مصاب بدلًا من ذلك، فسيمكنك تخيل مدى سوء الوضع وتفاقمه بسرعة كبيرة.
يستمر عدد الأشخاص الذين يصابون بمرض ما في الازدياد حتى يتجاوز معدل تعافي المصابين معدل إصابة الأشخاص المعرضين للعدوى. إذا نقل كل شخص مصاب العدوى إلى أقل من شخص واحد آخر في اليوم في المتوسط، فنتوقع حينئذ وجود عدد أقل من حالات الإصابة كل يوم وسوف يختفي المرض في نهاية المطاف. وبصرف النظر عن حدوث ذلك من عدمه، يعتمد الوقت الذي يستغرقه ذلك على حجم المجموعة السكانية ومقدار المخالطات الشخصية للأشخاص داخل المجموعة السكانية2.
في الشكل رقم 2، نقارن ما حدث لعدد الأشخاص المعرضين للإصابة والمصابين والمتعافين ضمن مجموعة سكانية في حالة R0 > 1 في مقابل R0 < 1. في الشكل 2A (الذي تكون فيه قيمة R0 أكبر من 1، يمكن أن يكون عدد الأشخاص الذين يصابون بالعدوى في الوقت ذاته مرتفعًا للغاية (انظر المنحنى البرتقالي)، ويجوز ألا يكون لدى المستشفيات القدرة على علاج كل شخص يُصاب بالعدوى. عندما تكون قيمة R0 أصغر من 1 ( R0 < 1) (انظر الشكل 2B)، لن ينتقل المرض إلى الكثير من الأشخاص في المجموعة السكانية، ومن ثم يصبح منحنى الأشخاص المصابين بمرور الوقت أكثر تسطيحًا. هذا السيناريو مُحبب، فإذا انتشر مرض ما بسرعة، فسنرغب في إبطاء حالات العدوى و”تسطيح المنحنى”3 (انظر الشكل 3).
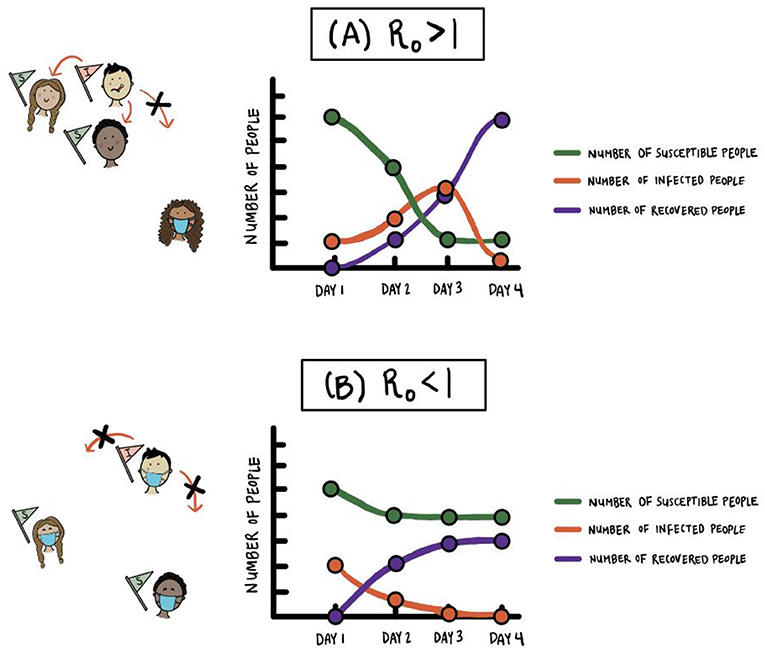
- شكل 2 - مقارنة عدد الأشخاص المعرضين للإصابة والمصابين والمتعافيين في نموذج SIR لمرض معدٍ.
- تشير القيم الموجودة على المحور الرأسي إلى جميع الأشخاص الموجودين في الأقسام المعرضين للإصابة والمصابين والمتعافيين في كل يوم (وليس فقط حالات العدوى وحالات التعافي الجديدة في ذلك اليوم). (A) عندما يكون R0 > 1، فإن عدد الأشخاص الذين يصابون في الوقت نفسه قد يكون كبير جدًا ويجوز ألا يكون لدى المستشفيات قدرة على علاج كل الأشخاص. نظرًا لأن الجميع تقريبًا يصابون في النهاية في هذه الحالة، يصبح عدد الأشخاص المعرضين للإصابة في النهاية صغيرًا جدًا. (B) عندما تبلغ قيمة R0 أقل من 1، في الحالات مثل ارتداء الكثير من الأشخاص الكمامات وتطبيق التباعد الجسدي، لن ينتقل المرض إلى العديد من الأشخاص ضمن المجموعة السكنية.
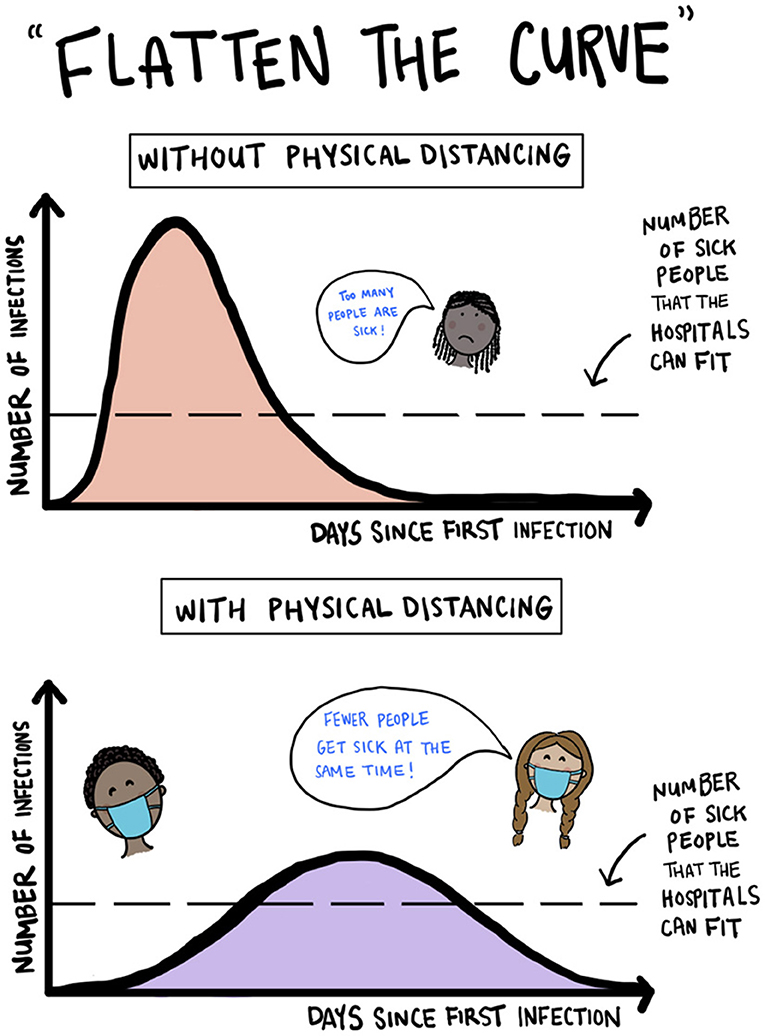
- شكل 3 - توضيح ”تسطيح منحنى” العدوى باستخدام التباعد الجسدي.
- (الشكل الخاص بنا مستوحى من صور مثل تلك الصورة على https://commons.wikimedia.org/wiki/File:Covid-19-curves-graphic-social-v3.gif by Siouxsie Wiles and Toby Morris.)
السياسات والسلوكيات و”تسطيح المنحنى”
عند التفكير بشأن كيفية انتشار مرض ما، تعتبر شبكات المخالطات الشخصية مهمة لتقدير قيمة R0 [4, 6]. تتصل أنت وأصدقاؤك مع بعضكم بعضًا في شبكة اجتماعية، وكذلك أبواك وأصدقاؤهم. لذلك، إذا أُصيب أحد أصدقائك بمرض ما، فيجوز أن ينتقل إليك ومن ثم إلى أبويك وإلى أصدقائهم بعد ذلك. قد ينقل الأشخاص المصابون، الذين يلتقون بالعديد من أصدقائهم شخصيًا، العدوى إلى العديد من الأشخاص.
استجابت العديد من الحكومات لجائحة كوفيد-19 عن طريق إغلاق المدارس وإلغاء الأحداث الرياضية والتجمعات الكبيرة الأخرى وعزل الأشخاص المصابين ومطالبة الأشخاص بملازمة المنزل وممارسة التباعد الجسدي نظرًا لمدى سهولة إصابة الأشخاص بفيروس سارس-كوف-2، واحتمالية إصابتهم بإعياء شديد بسبب كوفيد-19. الهدف من هذه الأنواع من السياسات والسلوكيات أثناء الجائحة هو محاولة الحد من المخالطات الشخصية المباشرة وغير المباشرة وبالتالي ”تسطيح منحنى” عدد المصابين (انظر الشكل 3) [3, 4, 6]. مع تطبيق مثل هذه الإجراءات والتدابير، إلى جانب ارتداء الكمامات وغسل اليدين كثيرًا، يتوزع عدد المصابين على فترة زمنية أكبر وتكون ذروته أقل، مما يشير إلى أن الحد الأقصى لعدد الأشخاص المصابين في أي يوم أقل مما لو كان الحال خلاف ذلك. هذا مهم حتى تتمتع المستشفيات بالقدرة على علاج أكبر عدد ممكن من الأشخاص. وبتحقيق حالة المنحنى المسطح، يواصل المرض انتشاره لكنه ينتشر ببطء أكثر، بحيث يتسنى للمستشفيات علاج المصابين الذين يحتاجون للمساعدة. وهذا يقلل عدد الوفيات الناتجة عن مرض ما. يقلل كذلك تسطيح المنحنى العدد الإجمالي للأشخاص المصابين بمرور الوقت.
الاستنتاجات
تلعب النماذج الرياضية والحوسبة دورًا كبيرًا في التأثير على استجابات الحكومات لجائحة كوفيد-19. وتكون هذه النماذج مفصلة أكثر مقارنة بنموذج SIR الذي ناقشناه أعلاه4. على سبيل المثال، تتضمن العديد من النماذج قسمًا للأشخاص الذين لا يعانون من أعراض ولا يزال يمكنهم نقل العدوى إلى الآخرين وتشمل بعض النماذج قسمًا للأشخاص الذين تطلبت حالتهم دخول إلى المستشفى.
توضح جائحة كوفيد-19 الحالية مدى أهمية النمذجة الرياضية للأمراض المعدية. تسمح المناهج الرياضية والحاسوبية للأشخاص بإحراز تقدم في الحد من انتشار مرض ما، بينما يطور الباحثون اللقاحات والعلاجات للقضاء عليه. كما أنها تساعد الجهود في تصميم التدخلات وبرامج التحصين.
مسرد للمصطلحات
الجائحة (Pandemic): ↑ الانتشار الواسع لمرض معدٍ عبر عدة قارات أو حتى في جميع أنحاء العالم.
النمذجة الرياضية (Mathematical Modeling): ↑ النموذج الرياضي هو عبارة عن وصف مبسط لشيء ما باستخدام قواعد الرياضيات ولغتها. يُعرف تطوير واختبار وتحسين نموذج كهذا باسم النمذجة الرياضية. ويعد نموذج SIR (المعرضون للإصابة (S) - المصابون (I) - المتعافون (R)) المتعلق بانتشار الأمراض المعدية مثالًا على أحد النماذج الرياضية.
اختصاصي النمذجة الرياضية للأوبئة (Mathematical Epidemiologist): ↑ عالم يدرس الأمراض المعدية باستخدام النمذجة والحوسبة الرياضية.
التنبؤ (Forecast): ↑ نوع من التوقع يقدم مجموعة من الاحتمالات للنتائج المستقبلية. على سبيل المثال، قد تقول نشرة الأرصاد الجوية في نشرة الأخبار أن هناك احتمال بنسبة 42% لسقوط أمطار على لوس أنجلوس غدًا. وكذلك قد يتنبأ عالم بمعدل عدد الأشخاص في لوس أنجلوس الذين سوف يصابون بكوفيد-19 خلال عام 2021.
النموذج المجزأ (Compartmental Model): ↑ النوع الأكثر شيوعًا من النماذج الرياضية الذي يستخدمه الباحثون للتنبؤ بكيفية انتشار مرض ما. يتألف النموذج المجزأ لانتشار مرض معد من فئات مختلفة (مثل ”المصابون” و”المتعافون”) التي يُطلق عليها ”أقسام” والقواعد الرياضية لكيفية انتقال الأشخاص من قسم إلى آخر. على سبيل المثال، باستخدام نموذج المعرضين للإصابة والمصابين والمتعافين (SIR)، يمكننا دراسة كيف يتغير عدد المعرضين للإصابة والمصابين والمتعافين في مجموعة سكانية على مدار الوقت.
المخالطة (Contact): ↑ تفاعل من أي نوع بين فردين. يمكن أن تكون المخالطة الشخصية إما مباشرة (مثل المصافحة) أو غير مباشرة (مثل لمس نفس السطح أو مجرد التواجد في مكان قريب).
عدد التكاثر الأساسي (Basic Reproduction Number (R0)): ↑ عدد حالات العدوى، في المتوسط، الناتجة عن شخص مصاب واحد ضمن مجموعة سكانية من الأشخاص المعرضين للإصابة.
النمو الأسي (Exponential Growth): ↑ نوع فائق السرعة من النمو. عندما يزداد المرض بشكل سريع، يتضاعف عدد الأشخاص المصابين بما يتناسب مع العدد الحالي من الأشخاص المصابين. على سبيل المثال، إذا كان هناك شخص واحد مصاب في اليوم الأول الذي يصيب فيه مرض شخص ما ضمن مجموعة سكانية، فسيزداد عدد الأشخاص المصابين بمقدار ثلاثة أمثال كل يومين، حينئذ سيكون هناك ثلاثة مصابين في اليوم الثالث، وتسع مصابين في اليوم الخامس، و27 مصابًا في اليوم السابع، و81 مصابًا في اليوم التاسع وهلم جرا.
إقرار تضارب المصالح
يعلن المؤلفون أن البحث قد أُجري في غياب أي علاقات تجارية أو مالية يمكن تفسيرها على أنها تضارب محتمل في المصالح.
شكر وتقدير
نشعر بالامتنان إزاء قرائنا الصغار - Emily Chen، وNia Chiou، وTaryn Chiou، وDimitri Chrysafis، وMaria Chrysafis، وValerie K. Eng، وIris Leung، وTalan Li، وAdam Lindemood، وSuzanna Lindemood، وEli Truong - لتعليقاتهم العديدة المفيدة. كما نشكر والديهم ومعلميهم وأصدقاءهم - Alena Carter وLyndie Chiou وChristina Chow - لجعلنا على اتصال معهم والتماس آرائهم. نشكر John Butler وFrancesca Henderson وRachel Levy وJoel Miller ومحررينا ومعلقينا على التعليقات المفيدة. وإذ تعترف MAP بالدعم المقدم من المؤسسة الوطنية للعلوم (رقم المنحة DMS-2027438) من خلال برنامج RAPID، وتعترف MAP وYHK بالدعم المقدم من مؤسسة العلوم الوطنية (رقم المنحة 1922952) من خلال برنامج خوارزميات الكشف عن التهديدات (ATD).
الحواشي
1. ↑ طالع Zaman [3] من أجل التعرف إلى المزيد عن الجائحات وAlberca et al. [1] وSalathé and Case [4] للحصول على مقدمة ميسرة لجائحة كوفيد-19.
2. ↑ جرّب نموذج SIR التفاعلي في Edenharter [7]. يمكنك أيضًا إلقاء نظرة على المناقشات في Weinersmith et al. [6] وZaman [3] وفي المناقشات والمحاكات التفاعلية في Salathé and Case [4]
3. ↑ الآن بعد أن ناقشنا R0 بتفاصيل أكثر، ألق نظرة أخرى على ما يحدث عندما تغير كميات، مثل معدلات الإصابة ومعدلات التعافي في المحاكاة التفاعلية في Edenharter [7].
4. ↑ طالع Ferguson et al. [8] للحصول على تفاصيل عن أحد النماذج التي تم استخدامها في المملكة المتحدة.
المراجع
[1] ↑ Alberca, G. G. F., Fernandes, I. G., Sato, M. N., and Alberca, R. W. 2020. What is COVID-19? Front Young Minds 8:74. doi: 10.3389/frym.2020.00074
[2] ↑ World Health Organization. 2020. Coronavirus Disease (COVID-19) Pandemic. Available online at: https://www.who.int/emergencies/diseases/novel-coronavirus-2019.
[3] ↑ Zaman, L. 2020. Developing an Intuition for Pandemics. Available online at: https://infectiousmatter.com/
[4] ↑ Salathé, M., and Case, N. 2020. What Happens Next? COVID-19 Futures, Explained With Playable Simulations. Available online at: https://ncase.me/covid-19/?v=3
[5] ↑ Brauer, F., Castillo-Chavez, C., and Feng, Z. 2019. Mathematical Models in Epidemiology. Heidelberg, Germany: Springer-Verlag.
[6] ↑ Weinersmith, Z., Koerth, M., Bronner, L., and Mithani, J. 2020. A Comic Strip Tour of the Wild World of Pandemic Modeling. Available online at: https://fivethirtyeight.com/features/a-comic-strip-tour-of-the-wild-world-of-pandemic-modeling/
[7] ↑ Edenharter, G. 2015. The Classic SIR Model. Available online at: https://maple.cloud/app/4837052487041024
[8] ↑ Ferguson, N. M., Laydon, D., Nedjati-Gilani, G., Imai, N., Ainslie, K., Baguelin, M., et al. 2020. Report 9: Impact of Non-pharmaceutical Interventions (NPIs) to Reduce COVID-19 Mortality and Healthcare Demand. Available online at: https://www.imperial.ac.uk/mrc-global-infectious-disease-analysis/covid-19/report-9-impact-of-npis-on-covid-19/
