תַקצִיר
האם ידעתם שאתם מקבלים בממוצע 35,000 החלטות בכל יום, כאשר חלק מההחלטות האלה לא חשובות יחסית, כמו ההחלטה מה לאכול לארוחת בוקר. אולם להחלטות אחרות יש השפעה גדולה יותר על עתידכם, כמו למשל בחירה של איזו אוניברסיטה ללכת אליה. כשאתם מתמודדים עם החלטה קשה, כיצד אתם שוקלים כל אפשרות כדי לבחור את הטובה ביותר? תהליך ההיררכיה האנליטית הוא שיטה אחת שבה אתם יכולים להשתמש. היא מסייעת לכם לקבל החלטות קשות על ידי השוואת אלטרנטיבות שונות לצורך ביצוע הבחירה הטובה ביותר.
מהו תהליך ההיררכיה האנליטית?
כיצד אתם מקבלים החלטות מורכבות כשאין תשובה ברורה מאליה? דמיינו שאתם צריכים לרכוש אופניים חדשים. זוג אופניים א זול יותר מזוג אופניים ב, אולם לזוג ב יש יותר אפשרויות מלזוג א. איזה קריטריון חשוב יותר – מחיר או אפשרויות? או האם משהו אחר? לעיתים אנו מקבלים החלטות על ידי מעקב אחרי תחושת הבטן שלנו או הסתמכות על נסיון העבר. אנו גם מחפשים עצות של אחרים או יוצרים רשימה של יתרונות ושל חסרונות. שיטה אחרת שיכולה לסייע לכם לעבד את המידע ולקבל החלטות נקראת תהליך היררכיה אנליטית (AHP). היררכיה היא מערכת דירוגים של אפשרויות שונות האחת כנגד השנייה, בהתבסס על חשיבוּת.
תהליך ההיררכיה האנליטית מסייע במיוחד כשאתם מקבלים החלטה שאין לה תשובה טובה ביותר באופן מובהק. אולי ישנם יותר קריטריונים שמעורבים בהחלטה – לא רק שניים כמו בדוגמה של האופניים. תהליך ההיררכיה האנליטית מערב מתמטיקה ופסיכולוגיה כדי להשוות כמה אפשרויות ולבחור את הטובה ביותר [1]. הוא עושה זאת באמצעות תפיסה שנקראת השוואות זוגות. במקום להשוות כמה קריטריונים בבת אחת, משווים שניים בכל פעם. באופן הזה, הבחירה נעשית קלה יותר.
אלגברה ליניארית היא ענף במתמטיקה שמסייע לנו לחשב את החשיבוּת של קריטריונים תוך שימוש במטריצוֹת. תהליך ההיררכיה האנליטית משתמש באלגברה ליניארית כדי להעריך את התוצאות של כל השוואת זוגות. כל קריטריון מקבל את משקל החשיבות שלו. ככל שהמשקל גבוה יותר, כך הקריטריון חשוב יותר להחלטה הכוללת. השיטה הזו של השוואה יכולה להיות מיושמת על החלטות רבות. לדוגמה, אתם יכולים להשתמש בה כדי לבחור מוצר או שירות, כמו למשל רכב או טיסה. אתם גם יכולים להשתמש בה כדי לבחור את התהליך או הנתיב המועיל ביותר, כמו למשל הערכה אם להשתמש בתחבורה פרטית או ציבורית כדי להגיע לבית הספר [2].
תהליך ההיררכיה האנליטית משמש באופן יומיומי בתעשיות הייצור, העסקים, ההנדסה ותעשיות אחרות. לדוגמה, הוא יכול לשמש כדי לתעדף תחזוקה של מבנים ציבוריים, כמו למשל גשרים [3]. כיום ישנם 56,000 גשרים בארצות הברית שזקוקים לתיקונים. התיקונים האלה צפויים לעלות 123 מיליארד דולר. אולם אין מספיק כסף בתקציב כדי לתקן כל גשר. לכן, מהנדסים משתמשים בתהליך ההיררכיה האנליטית כדי לפתח מערכת שמדרגת גשרים. מערכת הדירוג הזו מחליטה אלה גשרים לתחזק, בהינתן תקציב מוגבל. המערכת שוקלת את הבטיחות, השימוש, נוֹחוּת הנסיעה והיכולת לספוג נזק שיש לכל גשר.
המהנדסים השתמשו בהשוואות זוגות במטרה לשקול ולהשוות ארבעה קריטריונים ל-2,988 גשרים בארצות הברית. בהתבסס על ארבעת הקריטריונים, כל גשר קיבל דירוג כללי, מ“מצוין” ועד ל“נכשל”. המהנדסים מצאו שאף אחד מהגשרים שהם העריכו לא קיבלו ציון מעל ל“טוב”. למעשה, 75% מכל הגשרים במחקר שלהם היו רק “משביעי רצון”, או גרוע מכך! הדירוגים הפנו תשומת לב לבעיות עם התשתית של ארצות הברית, ויכלו להביא להקצאה של כסף נוסף לתחזוקה ולתיקונים. הדירוגים האלה גם אומרים לנו אלה גשרים צריך לתקן קודם. ההחלטה הזו של איזה גשר לתקן יכולה אפילו להציל חיים!
כיצד אנו משתמשים בתהליך ההיררכיה האנליטית?
תהליך ההיררכיה האנליטית כולל ארבעה צעדים:
(1) זהַו אּת ההחלטה, האפשרויות והקריטריונים
(2) ערכו השוואות זוגות
(3) חשבו את משקל החשיבות של כל קריטריון
(4) זהַו אּת האפשרות הטובה ביותר על ידי חישוב משהו שנקרא פונקציית תועלת.
החלטה, אפשרויות וקריטריונים
כל החלטה מתחילה עם שאלה: איזו חלופה נכונה עבורכם? לדוגמה, אם יכולים להשתמש בתהליך ההיררכיה האנליטית כדי לבחור לאיזו אוניברסיטה ללכת. בתרחיש הזה, אתם עשויים לרצות להחליט אלה משלוש האפשרויות המועדפות (אוניברסיטאות B, A, או C) הכי טובה עבורכם. ברגע שאתם מבינים את השאלה ואת האפשרויות, אתם מחליטים אלה קריטריונים לשקול. אולי שלושת הקריטריונים החשובים ביותר הם מציאת בית ספר שהוא זול, ממוקם קרוב לבית ומדורג גבוה. ברגע שתזהו את הקריטריונים האלה, תוכלו להתחיל את תהליך השוואת הזוגות.
השוואת זוגות
הקריטריונים החשובים שזיהיתם מאורגנים במטריצות. מטריצה היא רשת עם מידע שמסודר בשורות ובעמודות. במטריצות תהליך ההיררכיה האנליטית, לכל קריטריון יש שורה וטור משלו. מטריצות הריבועים שמתקבלות מאפשרות השוואת זוגות של כל השילובים האפשריים של קריטריונים (איור 1).
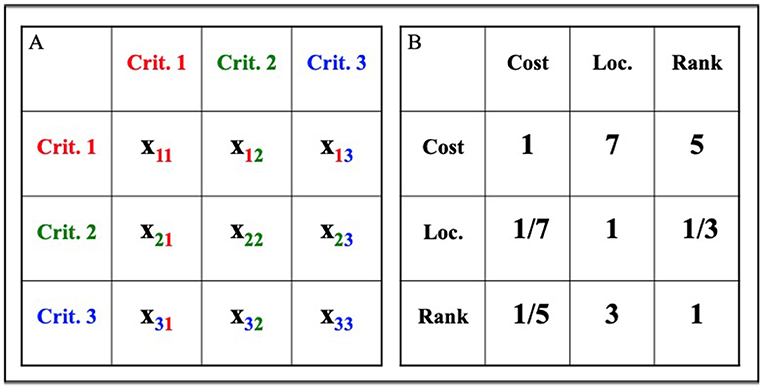
- איור 1 - מטריצות לדוגמה של תהליך ההיררכיה האנליטית.
- (A) מטריצה A היא דוגמת 3X3 של מטריצה. היא מראה כיצד השוואות של זוגות מאורגנות, ואפשר להתייחס אליה באמצעות ציונים תחתיים: לדוגמה, x12 מתייחס למרחב הרשת בשורה הראשונה ובעמודה השנייה. (B) מטריצת B היא גם מטריצת 3X3. היא מכילה את שלושת הקריטריונים של החלטת האוניברסיטה שלנו: עלות, מיקום ודירוג. בדוגמה הזו, כל מרחב רשת מכיל תוצאה מהשוואות זוגות. תוצאות הדגימה האלה מראות שהמחיר הוא גורם ההחלטה הכי חשוב, אחריו דירוג אקדמי, ולבסוף המיקום.
הצעד הראשון של השוואות זוגות הוא לשייך מספר לכל מרחב רשת. המספר הזה הוא החשיבות היחסית של שני הקריטריונים. לדוגמה, תוצאה של 1 משמעותה ששני הקריטריונים חשובים במידה זהה. כאשר קריטריון מושווה לעצמו, החשיבות היחסית היא 1, מאחר שהקריטריונים המושווים הם אותו דבר. מספרים גדולים יותר מראים קריטריון שהוא חשוב הרבה יותר, כאשר 9 היא התוצאה הגבוהה ביותר [1]. בשורה 1 באיור 1B, העלות גדולה פי 7 להחלטה הסופית ביחס למיקום (x12 = 7), וגדולה פי 5 (x13 = 5) מהדירוג האקדמי. תהליך הניקוד הזה חוזר על עצמו לכל מרחבי הרשת מימין לאלכסון (החצי הימני עליון של המטריצה).
מאחר שעלות חשובה פי 7 ממיקום, אנו יכולים להגיד שהמיקום חשוב פי 1/7 מהעלות (x21). באופן דומה, מאחר שהמחיר חשוב פי 5 מהדירוג האקדמי, הדירוג צריך להיות חשוב פי 1/5 מהעלות (x31). התהליך הזה של שימוש במספר הופכי (1/x) כדי לתאר את הקשר ההפוך שבין שני קריטריונים, חוזר על עצמו עבור כל מרחבי הרשת משמאל לאלכסון (החצי השמאלי התחתון של המטריצה). אם קריטריון 1 הוא חשוב פי x מקריטריון 2, אז קריטריון 2 צריך להיות חשוב פי 1/x מקריטריון 1.
משקולות חשיבות
המטריצה שהשלמנו משמשת לחישוב משקולות חשובות, שאומרות לכם כמה כל קריטריון ישתכלל לתוך ההחלטה שלכם. ככל שמשקולת החשיבות גדולה יותר לקריטריון נתון, כך תהיה לו יותר השפעה על ההחלטה הסופית שלכם. החלק הזה של תהליך ההיררכיה האנליטית מסתמך על אלגברה ליניארית. הצעד הראשון לקביעת המשקולת של קריטריון הוא למצוא ממוצע גיאומטרי (V) של שורה. הממוצע הגיאומטרי הוא סוג של ממוצע. אתם יכולים למצוא את הממוצע הגיאומטרי על ידי הכפלת כל התוצאות של חשיבות יחסית משורה (x) ולקיחת השורש ה-n של המכפלה הזו (כאשר n = מספר הקריטריונים הכולל). עדיף להשתמש בממוצע גיאומטרי מאשר בממוצע חשבוני (סכום חלקי n, או sum/n) עבור סוג החישוב הזה [4]. המשוואה הזו היא דוגמה שמראה לכם כיצד לחשב את הממוצע הגיאומטרי של קריטריון 1 של המטריצה הגנרית של 3X3 (איור 1A):
לאחר מכן, חלקו את מממוצע הקריטריון הגיאומטרי בסכום הממוצעים הגיאומטריים של של כל הקריטריונים. המספר העשרוני שהתקבל הוא המשקל (W) של אותו הקריטריון. השיטה הזו נקראת נִרְמוּל, מאחר שהיא מוודאת שהסכום של כל המשקלים שווה ל-1, או ל-100%. סכום המשקולות הוא 1 מאחר שכל קריטריון מהווה חלק מהחלטה אחת שלמה. המשוואה לדוגמה הזו מראה לכם כיצד לחשב את המשקולת של קריטריון 1 של המטריצה הגנרית 3X3 (איור 1A).
מה קורה אם אנו עושים את אותם החישובים לקריטריון של מחיר, תוך שימוש בתוצאות החשיבות היחסית מאיור 1B?
זה אומר לנו שהמחיר אחראי על 73% מההחלטה הכוללת ביחס לאיזו אוניברסיטה כדאי ללכת. באמצעות שימוש באותה השיטה, אנו מוצאים שהמשקולת המחושבת למיקום היא 8% והדירוג הוא 19%.
פונקציית התועלת: מי האפשרות הטובה ביותר?
הצעד הסופי של תהליך ההיררכיה האנליטית הוא לקבוע תועלת. תועלת היא מספר שמספק מידע על כמה משהו שימושי עבורכם, והיא תסייע לכם לאתר את האפשרות הטובה ביותר. ככל שקריטריון מועיל או שימושי יותר, כך התועלת שלו גדולה יותר. תועלת עשויה להימדד אחרת לכל קריטריון. בדוגמה שלנו, מחיר נמדד בדולרים. מיקום נמדד בקילומטרים מהבית. לדירוג אקדמי ניתן מספר, כאשר 1# מייצג את בית הספר במקום הראשון ומספרים גבוהים יותר מייצגים אוניברסיטאות פחות נחשבות. כאשר לקריטריונים יש יחידות שונות, עלינו להמיר אותם ליחידות סטנדרטיות שנקראות utiles (יחידה חסרת מידה של תועלת) באמצעות גרפים שנקראים פונקציות תועלת. באיור 2, אתם יכולים לראות כיצד אנו משתמשים בפונקציות תועלת בבחירת אוניברסיטה. התועלת הכללית מתחשבת בתועלת של כל קריטריון בודד ובחשיבות שלו להחלטה הכוללת. תועלת כללית שווה לסכום המכפלות של כל משקולות הקריטריונים עם ערך התועלת המתאים:
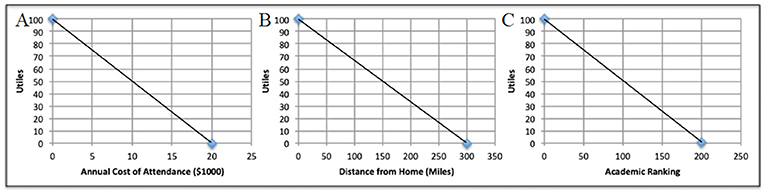
- איור 2 - פונקציות תועלת לדוגמה עבור תהליך ההחלטה לגבי אוניברסיטה.
- ביחס למחיר (משמאל), לבית ספר חינמי יש את התועלת המקסימלית האפשרית: 100 יחידות. אם שכר הלימוד גדול מתקציבכם, של 20,000 דולרים בשנה, יש לו תועלת מינימלית אפשרית: 0 יחידות. עבור מיקום (באמצע), אם מטרתכם להיות קרובים לבית, בית ספר שמרחקו 0 קילומטרים זוכה ב-100 יחידות. בית ספר שמרוחק ביותר מ-480 קילומטרים (300 מיילים) מקבל 0 יחידות. עבור דירוג אקדמי (מימין), בתי הספר שמדורגים במקום הראשון (1#) זוכים ב-100 יחידות. בית ספר שלא נכנס ל-200 הטובים ביותר מקבל 0 יחידות. (A) תועלת מחיר (B) תועלת מיקום (C) תועלת דירוג.
ברגע שכל הקריטריונים נמדדים, התועלת הכוללת של כל אפשרות נמצאת. דוגמה לחישוב תועלת עבור אוניברסיטה A היא:
באמצעות אותה השיטה, אנו מוצאים את נתוני התועלת הכללית לאוניברסיטאות B ו-C, כפי שמוצג בתיבה 1.
| מחיר ($) |
תועלת מחיר |
מיקום (מיילים) |
תועלת מיקום |
דירוג | תועלת דירוג |
תועלת כללית |
|
| A אוניברסיטה | 10,000 | 50 | 30 | 90 | 60 | 70 | 57.00 |
| B אוניברסיטה | 8,000 | 60 | 150 | 50 | 50 | 75 | 62.05 |
| C אוניברסיטה | 15,000 | 25 | 50 | 83.3 | 5 | 97.4 | 43.44 |
- טבלה 1 - נתוני אוניברסיטה לדוגמה. מחירים, מיקומים ודירוגים לדוגמה מוצגים בטבלה. המחיר, תועלות המחיר, המיקום והדירוג (ביחידות של utiles) מתקבלים מפונקציות התועלות מאיור 2. הערכים האלה הוכנסו לפונקציית התועלת כדי לחשב את התועלת הכוללת. התועלת הכוללת של כל אוניברסיטה מוצעת בטור השמאלי ביותר בטבלה.
בהתבסס על תוצאות תהליך ההיררכיה האנליטית, אוניברסיטה B היא הבחירה הטובה ביותר. כפי שאפשר לראות בטבלה 1, לאוניברסיטה B יש את התועלת הכוללת הגבוהה ביותר, 62.05. הסיבה לכך היא שהיא האפשרות הזולה ביותר, והמחיר מהווה 73% מההחלטה הכוללת. הודות למיקום המעולה שלה, אוניברסיטה A קרובה ונמצאת במקום השני, עם תועלת כוללת של 57.00. אף על פי שאוניברסיטה C היא בית הספר שמדורג הכי גבוה, יש לה תועלת כללית נמוכה הרבה יותר (43.44) משתי האחרות כתוצאה מהמחיר הגבוה שלה, כך שהיא הבחירה הכי פחות טובה.
סיכום
תהליך ההיררכיה האנליטית הוא כלי חזק שיכול לשמש אתכם בבית, בבית הספר, או בעבודה. הוא מסיר הטיות מתהליך קבלת ההחלטות, ומוודא שההחלטה שאתם מקבלים משקפת את הערכים ואת העדיפויות שלכם. בפעם הבאה שאתם ניצבים בפני החלטה מורכבת, שקלו להשתמש בתהליך ההיררכיה האנליטית כדי לקבל את החלטתכם. האפשרויות הן בלתי נדלות–שיטת תהליך ההיררכיה האנליטית מוגבלת רק על ידי מידת היצירתיות שלנו בשימוש בה.
מילון מונחים
תהליך היררכיה אנליטית (Analytic Hierarchy Process): ↑ שיטת קבלת החלטות שמשווה בין חלופות רבות, שכל אחת מכילה כמה קריטריונים, כדי לסייע לבחור את האפשרות הטובה ביותר.
השוואת זוגות (Pairwise Comparison): ↑ התהליך של השוואת זוגות קריטריונים זה מול זה.
אלגברה ליניארית (Linear Algebra): ↑ ענף במתמטיקה שעוסק בפונקציות ליניאריות, מרחבים וקטוריים, ומטריצות.
פונקציית תועלת (Utility): ↑ ייצוג מספרי של כמה משהו שימושי או מועיל עבורכם.
מטריצה (Matrix): ↑ רשת עם מידע, כמו למשל מספרים, אותיות וסמלים שמסודרים בשורות ובעמודות.
ממוצע גיאומטרי (Geometric Mean): ↑ הערך הממוצע של סֶט מספרים שנמצא על ידי שימוש בכפל של המספרים, ולא בסכום שלהם.
Utile: ↑ מידה חסרת יחידות שמשמשת לעשות סטנדרטיזציה של יחידות מקריטריונים שונים.
הצהרת ניגוד אינטרסים
המחברים מצהירים כי המחקר נערך בהעדר כל קשר מסחרי או פיננסי שיכול להתפרש כניגוד אינטרסים פוטנציאלי.
מקורות
[1] ↑ Ishizaka, A., and Labib, A. 2011. Review of the main developments in the analytic hierarchy process. Expert Syst. Appl. 38:14336–45. doi: 10.1016/j.eswa.2011.04.143
[2] ↑ Ho, W., and Ma, X. 2018. The state-of-the-art integrations and applications of the analytic hierarchy process. Eur. J. Oper. Res. 267:399–414. doi: 10.1016/j.ejor.2017.09.007
[3] ↑ Contreras-Nieto, C., Shan, Y., Lewis, P., and Hartell, J. A. 2019. Bridge maintenance prioritization using analytic hierarchy process and fusion tables. Autom. Construct. 101:99–110. doi: 10.1016/j.autcon.2019.01.016
[4] ↑ Krejčí, J., and Stoklasa, J. 2018. Aggregation in the analytic hierarchy process: why weighted geometric mean should be used instead of weighted arithmetic mean. Expert Syst. Appl. 114:97–106. doi: 10.1016/j.eswa.2018.06.060