ملخص
هل تعلم أنك تأخذ ما معدله 35000 قرار في اليوم الواحد؟ بعض هذه القرارات ليست مؤثرة بدرجة كبيرة، مثل تحديد ما تتناوله على وجبة الفطور، بينما يكون للبعض الآخر تأثير كبير على مستقبلك، مثل اختيار الجامعة التي تذهب إليها. عندما تقف أمام قرار صعب، كيف ستفكر في كل خيار لتحديد الأفضل بالنسبة إليك؟ يمكنك حينئذٍ استخدام عملية التحليل الهرمي، حيث إنها تساعدك على اتخاذ القرارات المهمة من خلال مقارنة العديد من البدائل لتحديد الخيار الأفضل.
ما هي عملية التحليل الهرمي؟
كيف يمكنك اتخاذ قرارات معقدة دون وجود إجابة مفضلة واضحة؟ تخيّل أنك تحتاج إلى شراء دراجة جديدة. الدراجة A أقل سعرًا من الدراجة B، لكن الدراجة B تتمتع بمزايا أكثر من الدراجة A، وهو المعيار الأكثر أهمية لك، فأيهما تختار، التكلفة أم المزايا؟ أو ربما شيء آخر؟ في بعض الأحيان نتخذ قرارات من خلال اتباع غرائزنا أو استنادًا إلى التجارب السابقة. يمكننا أيضًا البحث عن مزيد من النصائح أو إعداد قائمة بالإيجابيات والسلبيات، وهي طريقة أخرى يمكنها مساعدتك على معالجة كافة المعلومات واتخاذ قرارك وتسمى عملية التحليل الهرمي (AHP). التسلسل الهرمي هو نظام لترتيب الخيارات المختلفة أمام بعضها البعض استنادًا إلى أهميتها.
تعد عملية التحليل الهرمي مفيدة للغاية عندما تتخذ قرارًا مع عدم وجود أي قرار أفضل بصورة محددة. قد يكون هناك المزيد من المعايير المتضمنة في القرار، وليس اثنين فقط كما هو الحال في مثال الدراجة. تجمع عملية التحليل الهرمي بين الرياضيات والفلسفة للمقارنة بين العديد من الخيارات وتحديد أفضلها [1]. ويتم ذلك بواسطة مفهوم يسمى المقارنة الزوجية. فبدلًا من المقارنة بين العديد من المعايير في المرة الواحدة، تتم المقارنة بين معيارين اثنين في المرة الواحدة. وبذلك، يكون الاختيار أسهل.
الجبر الخطي هو أحد أنواع الرياضيات التي تساعدنا على حساب مدى أهمية المعايير باستخدام المصفوفات. تستخدم عملية التحليل الهرمي الجبر الخطي لتقييم نتائج كل مقارنة من المقارنات الزوجية. يتخذ كل معيار مقدارًا معينًا من حيث الأهمية. كلما ازداد المقدار، زادت أهمية المعيار للقرار بأكمله. يمكن استخدام أسلوب المقارنة هذا مع العديد من القرارات. على سبيل المثال، يمكنك استخدامه لاختيار إحدى المنتجات أو الخدمات، مثل اختيار سيارة أو رحلة طيران جوي. كما يمكنك استخدامه أيضًا لاختيار العملية أو الطريق الأكثر فعالية، مثل تقييم ما إذا كنت تستخدم وسيلة نقل خاصة أو عامة للوصول إلى الكلية [2].
تُستخدم عملية التحليل الهرمي في التصنيع، والأعمال التجارية، والهندسة وغيرها من الصناعات. على سبيل المثال، يمكن استخدامها لتحديد أولوية صيانة الهياكل العامة، مثل الجسور [3]. يوجد حاليًا 56000 جسر في الولايات المتحدة بحاجة إلى الإصلاح. ستتكلف هذه الإصلاحات 123 مليار دولار أمريكي إجمالًا. ومع ذلك، لا يوجد ما يكفي من المال في الميزانية لإصلاح كل جسر. لذلك، استخدم المهندسون عملية التحليل الهرمي لوضع نظام لتقييم الجسر. يحدد نظام التقييم هذا أي من الجسور يجب صيانتها، في ظل الميزانية المحدودة، ويضع النظام في الاعتبار سلامة كل جسر، واستخدامه، وراحة القيادة عليه والقدرة على تحمل الضرر.
استخدم المهندسون المقارنات الزوجية للموازنة والمقارنة بين أربعة معايير لما يبلغ 2988 من الجسور الأمريكية. وفقًا للمعايير الأربعة، حصل كل جسر على تقييم إجمالي، بدءًا من ”ممتاز” إلى ”ضعيف”. وجد المهندسون أنه لم يتم تقييم أي من الجسور بأعلى من ”جيد”؛ فحوالي 75% من الجسور الخاضعة لدراستهم كان تقييمها ”مُرضٍ” فقط، أو أسوأ! جذبت التقييمات الانتباه للمشاكل التي تعانيها البنية التحتية للدولة والتي قد تحتاج إلى مزيد من المال لإجراء الصيانة والإصلاح. كما تخبرنا التقييمات أي من الجسور تحتاج إلى الإصلاح أولًا. هذا القرار بشأن أي من الجسور يجب إصلاحه من شأنه أيضًا أن ينقذ الأرواح!
كيف نستخدم عملية التحليل الهرمي؟
تتكون عملية التحليل الهرمي من أربع خطوات:
- تحديد القرار والخيارات والمعيار.
- إجراء المقارنات الزوجية.
- حساب مدى أهمية كل معيار.
- تحديد الخيار الأفضل من خلال حساب ما يسمى المنفعة.
القرار والخيارات والمعيار
يبدأ كل قرار بسؤال: ما البديل المناسب لك؟ على سبيل المثال، يمكنك استخدام عملية التحليل الهرمي لتحديد الجامعة التي يجب الذهاب إليها. في هذا السيناريو، قد ترغب في تحديد أي من خياراتك المفضلة الثلاثة (الجامعات A، أو B أو C) هو الأفضل لك. بمجرد أن تفهم السؤال والخيارات، ستحدد حينها أي من المعايير يهمك. قد تكون المعايير الثلاثة الأكثر أهمية بالنسبة لك هي العثور على كلية ميسورة التكلفة وتقع بالقرب من المنزل وذات تصنيف جيد. بمجرد أن تحدد هذه المعايير، يمكنك البدء في عملية المقارنة الزوجية.
المقارنات الزوجية
تُنظم المعايير المهمة التي حددتها في مصفوفات. المصفوفة هي شبكة تحتوي على معلومات منظمة في صفوف وأعمدة. في مصفوفات عملية التحليل الهرمي، لكل معيار الصف والعمود الخاص به. تتيح المصفوفات المربعة الناتجة بإجراء مقارنة زوجية لجميع تركيبات المعايير الممكنة (الشكل 1).
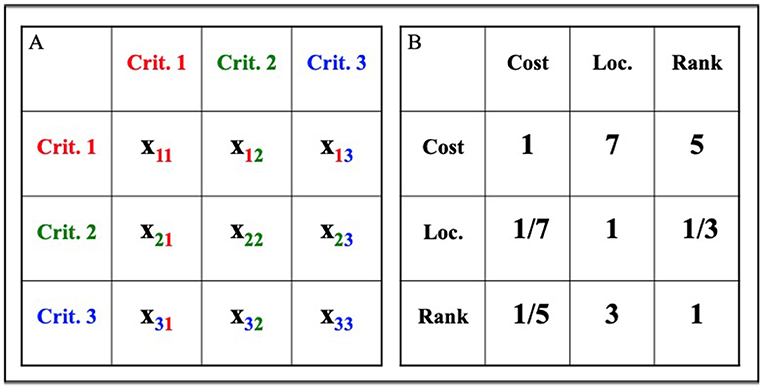
- شكل 1 - نموذج لمصفوفات عملية التحليل الهرمي.
- (A) المصفوفة أ هي نموذج مصفوفة 3 × 3. تعرض كيفية تنظيم المقارنات الزوجية والرجوع إليها باستخدام حروف سفلية: على سبيل المثال، x12 تشير إلى فراغ بالشبكة في الصف الثاني. (B) المصفوفة ب هي أيضًا مصفوفة 3 × 3، وهي تحتوي على ثلاثة معايير في قرار جامعتنا، وهي: التكلفة، والموقع والترتيب. في هذا المثال، يحتوي كل فراغ بالشبكة على درجة من المقارنات الزوجية. يوضح نموذج الدرجات هذا أن التكلفة هي الأهم في عامل اتخاذ القرار، ويليها الترتيب الأكاديمي وأخيرًا، الموقع.
الخطوة الأولى لإجراء المقارنات الزوجية هي تخصيص رقم لكل فراغ بالشبكة. يشير هذا الرقم إلى الأهمية النسبية لكلا المعيارين. على سبيل المثال، الدرجة 1 تعني أن كلا المعيارين لهما نفس الأهمية. عند مقارنة معيار بنفسه، تكون الأهمية النسبية له هي 1، ويرجع ذلك إلى إن المعيار الذي تجري مقارنته هو نفسه. تشير الأرقام الأكبر إلى أن المعيار يزداد أهمية بشكل متزايد، حيث تمثل 9 أعلى درجة [1]. في الصف 1 بالشكل (1B)، تكون التكلفة سبعة أضعاف أهميتها (x12 = 7) بالنسبة للقرار النهائي كموقع وخمسة أضعاف أهميتها (x3 = 5) كترتيب أكاديمي. تتكرر عملية تسجيل الدرجات هذه لجميع الفراغات بالشبكة على يمين القطر (النصف الأيمن العلوي من المصفوفة).
نظرًا لأن أهمية التكلفة سبعة أضعاف أهمية الموقع، يمكننا أيضًا أن نقول إن أهمية الموقع تبلغ 7/1 من أهمية التكلفة (x21). وبالمثل، نظرًا لأن أهمية التكلفة تبلغ خمسة أضعاف أهمية الترتيب الأكاديمي، فيجب أن تكون أهمية الترتيب 5/1 من أهمية التكلفة (x31). تستخدم هذه العملية المتبادلات، أو المعكوسات (1/x)، لوصف تكرار العلاقة العكسية بين معيارين لجميع الفراغات بالشبكة على يسار القطر (النصف الأيسر السفلي من المصفوفة). إذا كانت أهمية المعيار 1 × أضعاف أهمية المعيار 2، فيجب أن تكون أهمية المعيار 2 هي 1/× من أهمية المعيار 1.
مدى الأهمية
تُستخدم المصفوفة المكتملة بعد ذلك لحساب مدى الأهمية، والتي تخبرك إلى أي مدى سيؤثر كل معيار على قرارك. كلما ارتفع مدى أهمية المعيار الموضح، زاد تأثيره على قرارك النهائي. يعتمد هذا الجزء من عملية التحليل الهرمي على الجبر الخطي. الخطوة الأولى لتحديد مقدار المعيار هي إيجاد المتوسط الهندسي (V) للصف. المتوسط الهندسي هو أحد أنواع المعدلات. يمكنك إيجاد المتوسط الهندسي من خلال ضرب جميع درجات الأهمية النسبية من الصف (X) وأخذ الجذر nth من هذا الناتج (حيث n = إجمالي عدد المعايير) من الأفضل لهذا النوع من الحساب [4]. توضح هذه المعادلة النموذجية لك كيفية حساب المتوسط الهندسي للمعيار 1 من 3 × 3 من المصفوفة العامة (الشكل 1A):
ثم، اقسم المتوسط الهندسي للمعيار على مجموع المتوسطات الهندسية لجميع المعايير. نتيجة الكسر العشري هي مقدار (W) لذلك المعيار. تسمى هذه الطريقة بالتوحيد، لأنها تضمن أن يساوي مجموع جميع المقادير 1 أو 100%. مجموع المقادير هو 1 لأن كل معيار يعتمد على جزء من القرار بأكمله. توضح هذه المعادلة النموذجية لك كيفية حساب مقدار المعيار 1 من 3 × 3 في المصفوفة العامة (الشكل 1A):
ما الذي يحدث إذا أجرينا نفس الحسابات لمعيار التكلفة، باستخدام درجات الأهمية النسبية من الشكل (1B)؟
يخبرنا ذلك بأن التكلفة تحتسب 73% من إجمالي تحديد أي جامعة ستلتحق بها. باستخدام هذا الأسلوب نفسه، نجد أن المقدار الذي تم حسابه للموقع هو 8% والترتيب هو 19%.
المنفعة: ما الخيار الأفضل؟
الخطوة النهائية لعملية التحليل الهرمي هي تحديد المنفعة. المنفعة هي قيمة رقمية توفر معلومات حول مدى فائدة شيء ما لك، وسيساعدك ذلك على تحديد الخيار الأفضل. كلما زادت فائدة المعيار، ارتفعت المنفعة أكثر. يمكن قياس المنفعة بشكل مختلف لكل معيار. في المثال الذي ذكرناه، يتم قياس القدرة على تحمل التكاليف بالدولارات. يتم قياس الموقع بالأميال من المنزل. يمنح الترتيب الأكاديمي درجة، حيث يشير رقم 1 إلى الكلية الأعلى ترتيبًا (المركز الأول) وتشير الأرقام الأعلى إلى الجامعات الأقل صيتًا. عندما تحتوي المعايير على وحدات مختلفة، فإنه يتعين علينا تحويلها أولًا إلى وحدات قياسية تسمى منافع (مقياس منفعة عديم الوحدات) باستخدام مخططات تسمى دوال المنفعة. في الشكل 2، يمكنك مشاهدة الطريقة التي نستخدم بها دوال المنفعة في تحديد الجامعة. يشير إجمالي المنفعة إلى منفعة كل معيار على حدة وأهميته للقرار بأكمله. إجمالي المنفعة يساوي مجموع النواتج لكل مقدار للمعيار وقيمة المنفعة الخاصة به.
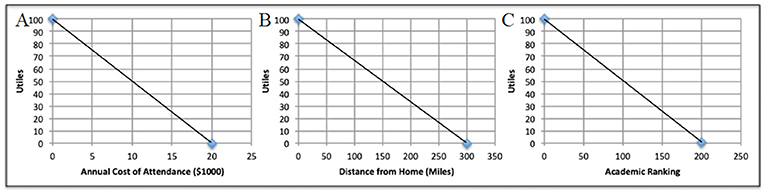
- شكل 2 - نموذج دوال المنفعة من أجل عملية تحديد الجامعة.
- بخصوص القدرة على تحمل التكاليف، تتميز الكلية ذات الرسوم الدراسية المجانية بأقصى منفعة ممكنة: 100 منفعة. إذا كانت الرسوم الدراسية تتجاوز ميزانيتك البالغة 20000 دولار أمريكي في العام، فإنها تتميز بأقل منفعة ممكنة: 0 منفعة. بخصوص الموقع، إذا كان هدفك أن تكون بالقرب من المنزل، فإن الكلية على بُعد 0 ميل تحقق 100 منفعة، بينما تحقق الكلية على بُعد 300 ميل 0 منفعة. بخصوص الترتيب الأكاديمي، تحقق الكلية الأعلى ترتيبًا (رقم 1) 100 منفعة، وتحقق الكلية التي لم تكن من ضمن أعلى 200 كلية 0 منفعة. A منفعة التكلفة. B منفعة الموقع. C منفعة الترتيب.
بمجرد أن يتم قياس المعايير الثلاثة كافة، يتم إيجاد إجمالي المنفعة لكل خيار. نموذج حساب المنفعة للجامعة A هو:

من خلال استخدام هذه الطريقة نفسها، نجد أن بيانات إجمالي المنفعة للجامعتين B وC، موضحة في الجدول 1.

- الجدول 1 - نموذج بيانات الجامعة.
- يتم توفير أمثلة على التكاليف، والمواقع والترتيب. قيم منفعة التكلفة، والموقع والترتيب (مقاسة بالمنفعة) هي من دوال المنفعة في الشكل 2. تم إدخال هذه القيم في دالة المنفعة لحساب إجمالي المنفعة. تتم مشاهدة إجمالي منفعة الجامعة في العمود بأقصى اليمين.
استنادًا إلى نتائج عملية التحليل الهرمي، تكون الجامعة B هي الاختيار الأفضل. كما هو موضح في الجدول 1، تتميز الجامعة B بأنها تحقق أعلى منفعة إجمالية، وهي 62.05، ويرجع ذلك إلى أنها الخيار الأقل تكلفة، وتحتسب التكلفة 73% من القرار بأكمله. بفضل موقعها الرائع، تأتي الجامعة A في المرتبة الثانية، محققة إجمالي منفعة بمقدار 57.00. وعلى الرغم من أن الجامعة C. من أعلى الكليات ترتيبًا، فإنها لديها منفعة إجمالية أقل بكثير (43.44) من الكليتين الأخريين نظرًا لتكاليفها المرتفعة، لذا تعد الخيار الأسوأ.
الخلاصة
تعد عملية التحليل الهرمي من الوسائل الفعالة التي يمكن استخدامها في المنزل، أو في الكلية أو في العمل، فهي تزيل الانحياز من عملية اتخاذ القرار وتضمن أن القرار الذي تتخذه يعكس قيمك وأولوياتك. في المرة التالية التي تتخذ فيها قرار صعب، فكر باستخدام عملية التحليل الهرمي لتحديد اختيارك. واعلم أن الاحتمالات لا حصر لها، وأن عملية التحليل الهرمي مقيدة فقط بإبداعك في استخدامها.
مسرد للمصطلحات
عملية التحليل الهرمي: ↑ هي إحدى الأساليب المتبعة لاتخاذ قرار، حيث نقارن بين العديد من البدائل، ولكل منها معايير للمساعدة على تحديد الخيار الأفضل.
المقارنة الزوجية (Pairwise comparison): ↑ هي عملية المقارنة بين معيارين في وقت واحد.
الجبر الخطي (Linear algebra): ↑ هو أحد فروع الرياضيات التي تهتم بالدوال الخطية، والفضاء المتجهي والمصفوفات.
المنفعة (Utility): ↑ هو تمثيل رقمي لمدى أهمية شيء ما أو فائدته لك.
المصفوفة (Matrix): ↑ هي شبكة تحتوي على معلومات، مثل الأعداد، والحروف والرموز المرتبة في صفوف وأعمدة.
المتوسط الهندسي (Geometric mean): ↑ القيمة المتوسطة لمجموعة من الأرقام وجدت باستخدام حاصل ضرب قيمها، بدلًا من المجموع.
المنفعة (Utile): ↑ هو مقياس عديم الوحدات للمنفعة يُستخدم لتوحيد الوحدات للمعايير المختلفة.
إقرار تضارب المصالح
يعلن المؤلفون أن البحث قد أُجري في غياب أي علاقات تجارية أو مالية يمكن تفسيرها على أنها تضارب محتمل في المصالح.
المراجع
[1] ↑ Ishizaka, A., and Labib, A. 2011. Review of the main developments in the analytic hierarchy process. Expert Syst. Appl. 38:14336–45. doi: 10.1016/j.eswa.2011.04.143
[2] ↑ Ho, W., and Ma, X. 2018. The state-of-the-art integrations and applications of the analytic hierarchy process. Eur. J. Oper. Res. 267:399–414. doi: 10.1016/j.ejor.2017.09.007
[3] ↑ Contreras-Nieto, C., Shan, Y., Lewis, P., and Hartell, J. A. 2019. Bridge maintenance prioritization using analytic hierarchy process and fusion tables. Autom. Construct. 101:99–110. doi: 10.1016/j.autcon.2019.01.016
[4] ↑ Krejčí, J., and Stoklasa, J. 2018. Aggregation in the analytic hierarchy process: why weighted geometric mean should be used instead of weighted arithmetic mean. Expert Syst. Appl. 114:97–106. doi: 10.1016/j.eswa.2018.06.060