תַקצִיר
במאמר זה אנו מספקים סקירה קצרה של מדע הרשתות באמצעות הדגשת החשיבות של מודלים של רשתות. נדבר על המקור של הרשתות ונתאר מחקרים ראשונים. לאחר מכן נסביר על התפקיד החשוב של רשתות גֶּנִים בביולוגיה עבור הבנת האופן שבו גנים גורמים לתכונות פיזיקליות מסוימות באורגניזמים. מלבד ביולוגיה, אפשר למצוא רשתות באופן בסיסי בכל תחומי המדע כולל כימיה, רפואה, עסקים, ניהול כספים ומדעי החברה. החברה הדיגיטלית שלנו מייצרת כמויות גדולות של נתונים ואפשר ליצור רשתות מהנתונים האלה באמצעות שיטות סטטיסטיות. ניתן להשתמש ברשתות האלה כדי לסייע לנו להבין היבטים שונים של החברה, ובסופו של דבר לספֵּר את חיינו.
מהן רשתות ומהיכן הן מגיעות?
מגדל בבל מספר את הסיפור התנ“כי שאלוהים בלבל את שפת האנשים בניסיונם לבנות מגדל שמגיע לגן עדן, באמצעות יצירת שפות שונות ביניהם. באופן הזה, האנשים כבר לא יכלו להבין זה את זה והיו צריכים לוותר על השגת המשימה. במובן מסוים, רשתות מספקות שפה מתמטית שמאפשרת למדענים מתחומים רבים שונים להבין זה את זה. הדבר גורם לרשתות להיות כלים חשובים שמאפשרים לנו לעבוד על הבעיות הקשות ביותר שניתן לדמיין [1]. התחום שמשתמש ברשתות במטרה לפתור בעיות מורכבות נקרא מדע הרשתות [2].
המושגים ”גרף“ ו”רשת“ משמשים לעיתים קרובות בצורה חלופית. באופן מסורתי, גרף מתייחס לאובייקט מתמטי שאינו זקוק לייצוג בעולם האמיתי. אף על פי שמתמטיקאים חקרו רשתות יותר מ-200 שנים (עם אנשים כמו Cayley ו-Euler), הרעיון של גרף הוא הרבה יותר עכשווי ויכול להיות מאותר אחורה למתמטיקאי בשם König בשנות ה-30’, לפני פחות מ-100 שנים. בצורתו הפשוטה ביותר, גרף מוגדר מתמטית על-ידי ההגדרה הזו:
הגדרה 1.1: הזוג (V, E) = G שבו V מייצגת קבוצה של צמתים (vertices) ו-E מייצגת קבוצה של קשתות (edges), נקרא גרף סופי בלתי מכוון (finite undirected graph).
אפשר להבין את ההגדרה באופן הבא: גרף מורכב משתי ישויות, צמתים שנקראים vertices (שמיוצגים על-ידי האות V) וקשתות שנקראות edges (שמיוצגות על-ידי E). כאן V הוא קבוצה שמכילה אלמנטים, לדוגמה: V = {a, b, c, …}, ו-E היא קבוצה אחרת שמכילה מידע על הקשרים שבין האלמנטים ב-V, לדוגמה: E = {(a, b), (a, c), …}. המונח מציין קבוצה אחרת שמכילה את כל זוגות הצמתים האפשריים שאפשר ליצור מכל הצמתים שמוכלים בקבוצה V. לכן, המשמעות היא דומה למקדמים בינומיים אם V הייתה מספר חיובי שלם. הסמל ⊆ ב- משמעותו שכל האלמנטים בקבוצה E גם מוכלים בקבוצה , ולכן E הוא תת-קבוצה של . זה כולל את המקרה שבו כל האלמנטים שב- הם גם ב-E. באיור 1 (משמאל) אנו מראים דוגמה מוחשית של רשת.
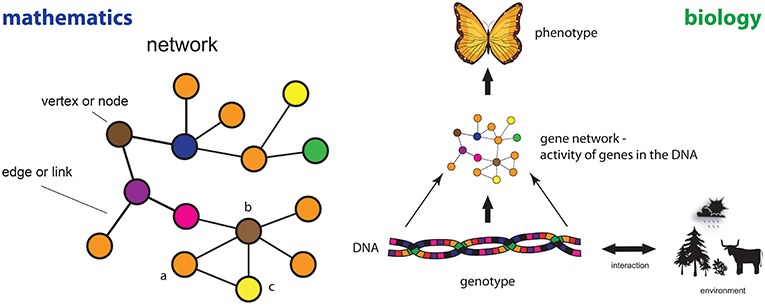
- איור 1 - משמאל: דוגמה של רשת מתמטית והחלקים שמגדירים אותה.
- מימין: העיקרון של נוף אפיגנטי (epigenetic landscape) שמתייחס לרשת של גנים בתור הקשר שבין גנוטיפ לבין אורגניזם (הדנ”א שלו) והפנוטיפ שלו (איך שהאורגניזם נראה).
אתם הקוראים עשויים לתהות לגבי האופן שבו נכתבת ההגדרה המתמטית של רשת. זה מה שנקרא הפשטה. אם רוצים לחקור רשתות באופן רציני, ניסוחים כאלה נמצאים בלב התחום, ובמערך הכישורים של החוקרים נדרש עניין להוט בהפשטה.
בין הרשתות המתמטיות הראשוניות שנחקרו היו רשתות אקראיות. Rényi ו-Erdös חקרו את הרשתות האלה בשנות ה-60. גרף אקראי עם N צמתים מתקבל על-ידי חיבור כל זוגות הצמתים עם הסתברות קבועה p. למרות הבנייה הפשוטה שלו, חקירת התכונות המתמטיות של הגרף הזה היא מורכבת באופן מפתיע, ודורות של מדענים עבדו על הבעיה הזו.
היכן מוצאים רשתות?
בביולוגיה, חשיבות של רשתות זוהתה מאחר שמערכות ותהליכים ביולוגיים צריכים להיחקר באופן הוליסטי (שמתייחס אל כל החלקים) [3]. משמעות הדבר היא שמערכות ביולוגיות לא יכולות להיות מצומצמות לחלקים קטנים אקראיים אלא שהגודל המינימלי של החלקים צריך להיות תפקודי במובן הזה שהאורגניזמים שנמצאים בבסיסו עובדים.
אחת התובנות הראשונות בהקשר הזה הייתה של Conrad Waddington, שהגה את הרעיון של נוף אפיגנטי בשנות ה-40 [4]. כאן אפיגנטיקה משמעותה חֵקֶר השינויים של פנוטיפ מורש (ראו איור 1) שלא משנה את הדנ“א. הרעיון הבסיסי מוצג באיור 1) (מימין). ברמה המולקולרית בתוך תא ביולוגי של אורגניזם (צמח, חיה או אדם), האינטראקציות שבין תוצרי גנים (חלבונים) יכולות להיות מיוצגות כרשת של גנים, כלומר כרשת שמווסתת תהליכי תעתוק, או רשת של חלבונים. ברשת הזו צמתים קשורים לגנים וקשתות קשורות לאינטראקציות שבין גנים. משמעות הדבר היא שרשתות מופיעות באופן טבעי בחקר אינטראקציות מולקולריות בתור הייצוג הגרפי והייצוג המתמטי שלהן [5]. כתלות בתכולת הדנ”א של אורגניזם והאינטראקציות שלו עם הסביבה (דיאטה, אורח חיים וכולי), מבנה רשת הגנים משתנה מאחר שתבניות הפעילות של הגנים משתנות, וכתוצאה מכך הפנוטיפ (ההופעה הפיזית, לדוגמה הצבע והצורה של כנפי פרפר) של אורגניזם מופיע.
אפשר להשתמש ברשתות בתחומים שונים רבים
רשתות הן כלים גמישים מאוד ואפשר להשתמש בהן בתחומים רבים מלבד ביולוגיה. הגמישות נובעת משלושה מאפיינים עיקריים של הרשתות. ראשית, הרשתות יכולות לקיים אינטראקציות מורכבות בין כל החלקים השונים של מערכת. שנית, רשתות יוצרות ייצוגים מתמטיים של המערכת שיכולים להיחקר ושאפשר לבצע עליהם מניפולציות. שלישית, רשת מייצגת מבנה נתונים שיכול להיות מאוחסן בנוחות על מחשב ומעובד בהרבה צורות שונות, לדוגמה באמצעות שיטות של מודלים סטטיסטיים למציאת קהילות צמתים שמחוברות באופן הדוק.
בשל הגמישות הזו משתמשים ברשתות בהרבה תחומים שונים כולל כימיה, פיזיקה, ביולוגיה, רפואה, עסקים, ניהול כספים ורשתות חברתיות. כאן ישנה רשימה של הרשתות החשובות ביותר מהתחומים האלה ומה אפשר לחקור בעזרתן:
- מבנים כימיים, במטרה לחקור תרכובות כימיות שקשורות זו לזו.
- רשתות מטאבוליות, במטרה לחקור כיצד אורגניזמים מבצעים פעולות כמו עיכול מזון, גדילה והתפתחות.
- רשתות תקשורת, במטרה לחקור את התקשורת המולקולרית בין חלבונים.
- רשתות לוויסות תהליכי תעתוק, במטרה לחקור אקטיבציה של גנים.
- רשתות של אינטראקציות בין חלבונים, במטרה לחקור היווצרות מורכבת.
- רשתות פיננסיות, במטרה לחקור תיקי עבודות (פורטפוליו) אופטימליים.
- מבני קבצים מבוססי גרפים, במטרה לחקור צורות כתיבה.
- רשתות של התנהגות צרכנים, במטרה לחקור הרגלי קנייה ברשת.
- רשתות כלכליות, במטרה לחקור תבניות סחר גלובלי.
- רשתות חברתיות, במטרה לחקור קשרים אנושיים.
באיור 2 אתם יכולים לראות שתי דוגמאות של רשתות אמיתיות. הרשתות האלה הן מסוג של רשת שנקרא bipartite network. רשת bipartite network מכילה שני סוגי צמתים, שמוצגים על-ידי שני צבעים (כחול וכתום). משמעות הצמתים האלה תלויה בבעיה שחוקרים. עבור הרשת החברתית שמוצגת באיור, הצמתים הכחולים קשורים לשחקנים והצמתים הכתומים קשורים לסרטים שבהם השחקנים שיחקו. לדוגמה, העובדה ש- Harrison Ford שיחק במלחמת הכוכבים מצוירת באיור 2. עבור רשת ניהול הכספים שמוצגת, הצמתים הכחולים קשורים למשקיעים והצמתים הכתומים קשורים למלאים שנקנו על-ידי המשקיעים. הראינו את הרשת החברתית ורשת ניהול הכספים כמשתרעות זו על זו מאחר שרצינו להדגיש שוב את האופי המופשט של הרשתות. בהקשר לשתי הרשתות האלה, אתם יכולים לתרגל את ההמחשה של המצב באמצעות התמקדות באחת מהרשתות כל פעם, והתעלמות מוחלטת מהשנייה. התרגיל הזה ילמד אתכם כיצד להתמודד עם המצב המופשט הזה.

- איור 2 - מוצגות שתי דוגמאות ליישום של הרשתות שמייצגות רשת חברתית ורשת ניהול כספים.
- כדי להפוך את הרשת שמשמאל למוחשית יותר התמקדו ראשית ברשת העליונה ואז התמקדו רק ברשת התחתונה. זה ייתן לכם שתי רשתות נפרדות. זה יבהיר לכם את המשמעות המופשטת של הרשת שמשמאל.
מה המשמעות של רשתות?
המשמעות המוחשית של רשתות והשימוש בהן תלוי בבעיות שהן מייצגות. לדוגמה, אנו עשויים להשתמש ברשת חברתית כדי להסתכל על שחקנים שקשורים זה לזה דרך סרטים שונים, במטרה לראות אלה שחקנים הופיעו יחד באותם הסרטים. באופן מעשי זה יכול להתקשר לשיוך שחקנים כתלות בז’אנרים של סרטים. עבור גרף שממדל חלבון אפשר לחקור את המודולים או קהילות המבנים של הצמתים. בפרט, אלה יכולים לייצג את מקטעי החלבונים שנשמרו במהלך האבולוציה. עבור רשת מחשבים אפשר לחקור כמה צמתים ניתן להסיר מהרשת ועדיין לשמור עליה מחוברת – באופן מעשי זה יכול להעיד על העמידות של רשת כזו ביחס להתקפות של האקרים. עבור רשת שמווסתת תהליכי תעתוק אפשר לזהות את הצמתים שיש להם יותר קשרים עם צמתים אחרים – באופן מעשי זה מגדיר גנים שמתפקדים כמו מרכזת, מה שעשוי להעיד על החשיבות שלהם.
אלה רק כמה דוגמאות שמתארות כיצד אפשר להשתמש ברשתות מופשטות במטרה לפתור בעיות מוחשיות בתחומי מחקר שונים.
כיצד אנו מקבלים את הרשתות?
בניגוד לרשתות שהוצגו באיור 2, שהן יחסית פשוטות וקלות להבנה, ישנן רשתות מורכבות. רשתות כאלה צריך להסיק מנתונים באמצעות יישום שיטות מסטטיסטיקה ומלמידת מכונה. באיור 3 אנו מספקים סקירה של היבטים בחברה הדיגיטלית שלנו שמאפשרים לנו לייצר כמויות אדירות של נתונים כמעט על כל היבט בחיים כולל בריאות (בדיקות רפואיות, סמארטפונים, שעונים חכמים וכולי); עסקים (שוק המניות, אמאזון וכולי), ורשתות חברתיות (טוויטר, פייסבוק וכולי). אפשר לנתח נתונים מהתחומים האלה בעזרתם של מחשבים במטרה להפיק מודלים של רשתות. מודלי הרשתות האלה יכולים לספק לנו תובנות חדשות על היבטים רבים בחברה שלנו כמו כלכלה, שיטות לטיפול רפואי במטופלים או התנהגות צרכנים, אשר אפשר להשתמש בהם כדי לשפר את חיינו.
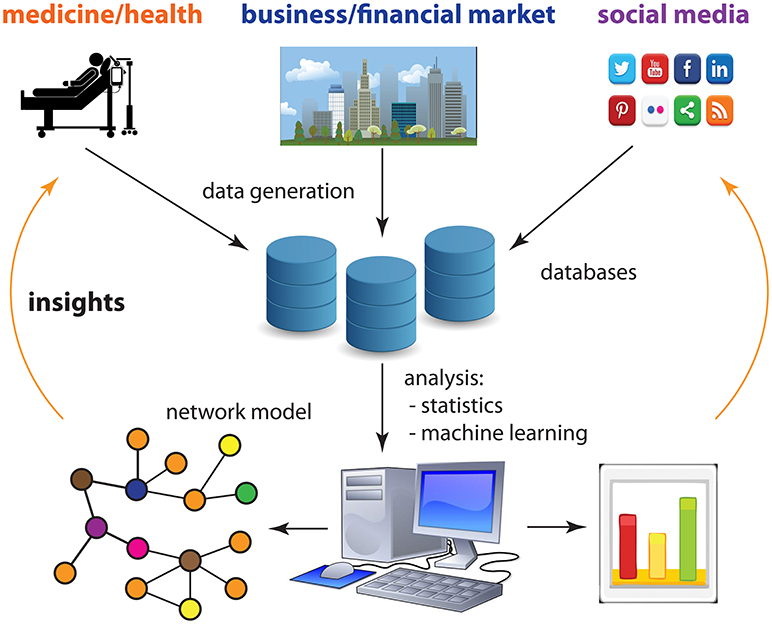
- איור 3 - החברה הדיגיטלית שלנו מאפשרת לנו לייצר כמויות אדירות של נתונים כמעט על כל היבט בחיים כולל בריאות, עסקים ורשתות חברתיות.
- אפשר לנתח את הנתונים האלה באמצעות מחשבים וליצור מודלים של רשת שילמדו אותנו דברים חדשים על החברה שלנו, ויאפשרו לנו לשפר את אותם התחומים בחברה.
מסקנות
אנו מקווים שהסקירה הקצרה שלנו הראתה לכם שרשתות מספקות שפה בסיסית שמאפשרת לנו להתמודד עם מרבית הבעיות המעניינות והחשובות בחברה שלנו ובמדע. אולם כדי להיות מסוגלים לחקור מודלים כאלה של רשתות נדרשת הבנה מתמטית חזקה.
המחברים
FE-S הגה את רעיון המחקר. כל הכותבים תרמו לכל ההיבטים של ההכנה והכתיבה של המאמר. כל הכותבים אישרו את הגרסה הסופית.
מילון מונחים
הגדרה מתמטית (Mathematical definition): ↑ תיאור שמבוטא בשפה מתמטית שהוא חשוב ויסודי מאוד במתמטיקה.
אפיגנטיקה (Epigenetics): ↑ חֵקֶר של שינויים בפנוטיפ המולד שלא מערבים שינויים בדנ“א. משמעות השם היא רכיבים שנמצאים על גבי (ביוונית הקידומת epi משמעותה ’על גבי’) הגנים.
דנ”א (DNA): ↑ חומצה דיאוקסיריבונוקלאית, חומר שמשכפל את עצמו ונוכח כמעט בכל האורגניזמים החיים כמרכיב הראשי של כרומוזומים, והוא נושא את המידע הגנטי.
הצהרת ניגוד אינטרסים
המחברים מצהירים כי המחקר נערך בהעדר כל קשר מסחרי או פיננסי שיכול להתפרש כניגוד אינטרסים פוטנציאלי.
מקורות
[1] ↑ Emmert-Streib, F., Dehmer, M., and Shi, Y. 2016. Fifty years of graph matching, network alignment and network comparison. Inform. Sci. 346–347:180–97. doi: 10.1016/j.ins.2016.01.074
[2] ↑ Barabási, A.-L. 2013. Network science. Philos. Trans. R. Soc. A 371:20120375. doi: 10.1098/rsta.2012.0375
[3] ↑ Emmert-Streib, F. and Dehmer, M. 2011. Networks for systems biology: conceptual connection of data and function. IET Syst. Biol. 5:185. doi: 10.1049/iet-syb.2010.0025
[4] ↑ Waddington, C. H. 1957. The Strategy of the Genes. London: George Allen & Unwin.
[5] ↑ Emmert-Streib, F. and Glazko, G. V. 2011. Network biology: a direct approach to study biological function. Wiley Interdiscipl. Rev. Syst. Biol. Med. 3:379–91. doi: 10.1002/wsbm.134
