תַקצִיר
איך אנו קובעים מי הדמויות החשובות בסרט כמו לשבור את הקרח? אנו יכולים לצפות בו, כמובן, אולם ישנן דרכים אחרות – באמצעות מתמטיקה ומחשבים – לראות מה חשוב בעולם החברתי של סיפור. הרעיון הוא לחשב מספרים הַמְּכֻנִּים מרכזיוּת (centrality), שמאפשרים למדוד מי האנשים החשובים ברשתות חברתיות. במאמר הזה נדבר על סוגים שונים של מדידת מרכזיוּת בדרכים שונות. נדון גם באופן שבו אנשים משתמשים במרכזיות כדי לחקור סוגים שונים של רשתות, לא רק רשתות חברתיות. מדענים מפתחים כיום מדידות מרכזיות שמביאות בחשבון גם שינויים לאורך זמן וסוגים שונים של קשרים.
הסרט לשבור את הקרח ורשתות חברתיות
האם ראיתם את הסרט לשבור את הקרח? הוא מספר את סיפורן של שתי אחיות יתומות, אלזה ואנה, שהן נסיכות בממלכת ארנדל. לאלזה יש כוח קסם שמאפשר לה ליצור שלג וקרח, אולם הקסם הזה מסוכן לאנשים שסביבהּ. כדי להגן על אנה, אלזה נמנעה ממנה מאז שהן היו קטנות מאוד. ביום ההולדת העשרים ואחד של אלזה, היא הוכתרה למלכת ארנדל. במסיבה לציון חגיגת ההכתרה שלה, היא מאבדת שליטה על יכולות הקסם שלה ומטילה על ארנדל כישוף שגוזר עליה חורף נצחי. אלזה נהיית מתוסכלת מאוד ועוזבת את ארנדל. אנה יוצאת למסע להשיב את אחותה ולשים קץ לכישוף החורף. לאורך הדרך היא פוגשת דמויות בלתי נשכחות כמו קריסטוף סוחר הקרח, חבריו הטרולים וכמובן איש השלג אולף. אנה גם הושפעה על-ידי הקסם של אלזה והיא מקוללת לקפוא ולהפוך בהדרגה לקרח, כך שחשוב מאוד עבור אנה וכל ארנדל לשבור את הקללה.
בלשבור את הקרח, דמויות רבות מכירות זו את זו, בין אם לפני שהסיפור התחיל ובין אם הן נפגשות במהלך הסרט. אלזה (כמובן) מכירה את אחותה אנה, שמכירה במהלך הסרט את קריסטוף, שמכיר את הטרולים. אוסף האנשים שמכירים זה את זה, בשילוב עם הקשרים שבין האנשים האלה, נקרא רשת חברתית. רשתות חברתיות הן חשובות. לדוגמה, הן מסייעות להפיץ ידע מאחר שאנשים מספרים זה לזה דברים כשהם מדברים או שולחים הודעות אחד לשני. בלשבור את הקרח, לדוגמה, אנה לומדת דרך רשת חברתית שהכישוף שלה יכול להירפא רק על-ידי מעשה של אהבת אמת. היא לומדת זאת מהטרולים, שאותם היא פגשה דרך קריסטוף.
רעיונות בסיסיים של מדידת מרכזיות
רשתות חברתיות יכולות להגיד לנו משהו על האנשים שבתוכן. כשמישהו נמצא במצב קשה הוא יכול להיעזר בחבריו. למי יש הכי הרבה חברים בלשבור את הקרח? קשה לקבוע זאת רק דרך צפייה בסרט, אולם אנו יכולים לחקור סוג אחר של רשת חברתית – הרשת של מי מדבר עם מי. הרשת הזו, שמוצגת באיור 1, אינה זהה לגמרי לרשת של חברויות, אולם קל הרבה יותר לקבוע במדויק מי מדבר עם מי בסרט מאשר להחליט בדיוק מי חבר של מי ועד כמה החברויות האלה חזקות. ברשת השיחות הזו אנה מדברת עם תשעה אנשים, אז אנו נניח שיש לה תשעה חברים. מתמטיקאים אומרים שאנה היא צומת ברשת הזו, שיש לה דרגה של תשע, ושתשעת החברים האלה הם השכנים שלה. באופן דומה, לאלזה יש דרגה של שמונה, מאחר שיש לה שמונה חברים; לקריסטוף יש דרגה של שש. חישוב הדרגה של מישהו היא דרך אחת למדוד את החשיבוּת שלו, אולם ישנן גם הרבה דרכים אחרות.
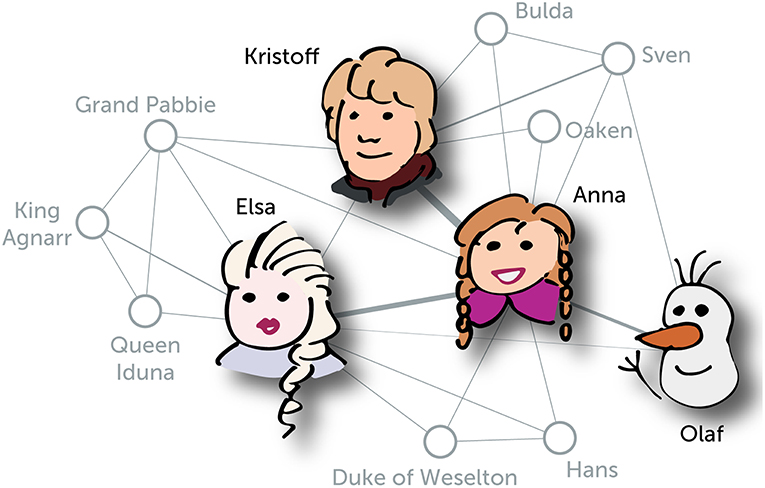
- איור 1 - רשת של שתי הדמויות הראשיות בלשבור את הקרח.
- הרשת הזו מראה מי מדבר עם מי בסרט. ככל ששתי דמויות מדברות יותר זו עם זו, כך הקו ביניהן עבה יותר. אנו מדגישים במיוחד את הדמויות החשובות בשחור. כל דמות, כמו אולף, היא “צומת” ברשת. אולף מדבר עם שלוש דמויות – אנה, אלזה וסוון – ברשת הזו, כך שאנו אומרים שיש לו “דרגה” של שלוש. אנה, אלזה וסוון הם ה“שכנים” של אולף ברשת.
התבוננו מקרוב באיור 1. האם אתם יכולים לפענח מי הדמות החשובה ביותר בלשבור את הקרח מהתבוננות ברשת שבתמונה הזו? לאנשים חשובים לעיתים קרובות יש הרבה חברים. יתרה מזו החברים של אנשים חשובים הם גם אנשים חשובים בעצמם. כדי למדוד את זה באמצעות מספר אנו מתחילים עם ההנחה שכל הדמויות (כלומר, הצמתים) חשובות באופן זהה, עם ערך ראשוני של 1. אנו מעדכנים את החשיבוּת (שנקראת מרכזיוּת בשפה של אנשים החוקרים רשתות) של כולם על-ידי סכימת החשיבויות של דמויות שאליהן הם מחוברים (במילים אחרות, השכנים שלהם). אחרי שעשינו זאת פעם אחת, התוצאה הראשונית זהה לדרגה – כלומר, למספר החברים של כל צומת. אנו מחלקים את המספרים האלה בסכום של החשיבויות של כל הצמתים (זה שומר על המספרים מהגעה לערך גבוה מדי) כדי לקבל קבוצה של חשיבויות חדשות. כשאנו חוזרים על זה שוב ושוב ומחליפים את החשיבות של כל צומת בסכום החשיבויות של השכנים שלו ומחלקים את התוצאה בסכום כל החשיבויות ברשת, החשיבויות בסופו של דבר מפסיקות להשתנות. נסו זאת בעצמכם באמצעות איור 2; עבור רשתות קטנות, המספרים בדרך כלל מפסיקים להשתנות במהרה. המספרים שאנו מקבלים בסוף החישוב נקראים מרכזיות וקטור עצמי, שם “מפוצץ” לסוג מסוים של חשיבות שאנו מחשבים. עבור הרשת באיור 1, אם אנו מביאים בחשבון באיזו תדירות דמויות מדברות זו עם זו, לאנה יש את הערך הכי גדול שעומד על 0.295. לפי המספרים האלה, אנה עדיין הדמות החשובה ביותר אולם כעת קריסטוף ממוקם מעל אלזה. אם אנו מתעלמים מהתדירות שבה דמויות מדברות זו עם זו, המספרים משתנים מעט: אנה עדיין ראשונה, עם 0.146; אלזה שנייה, עם 0.132; וקריסטוף כעת שלישי, עם 0.112.
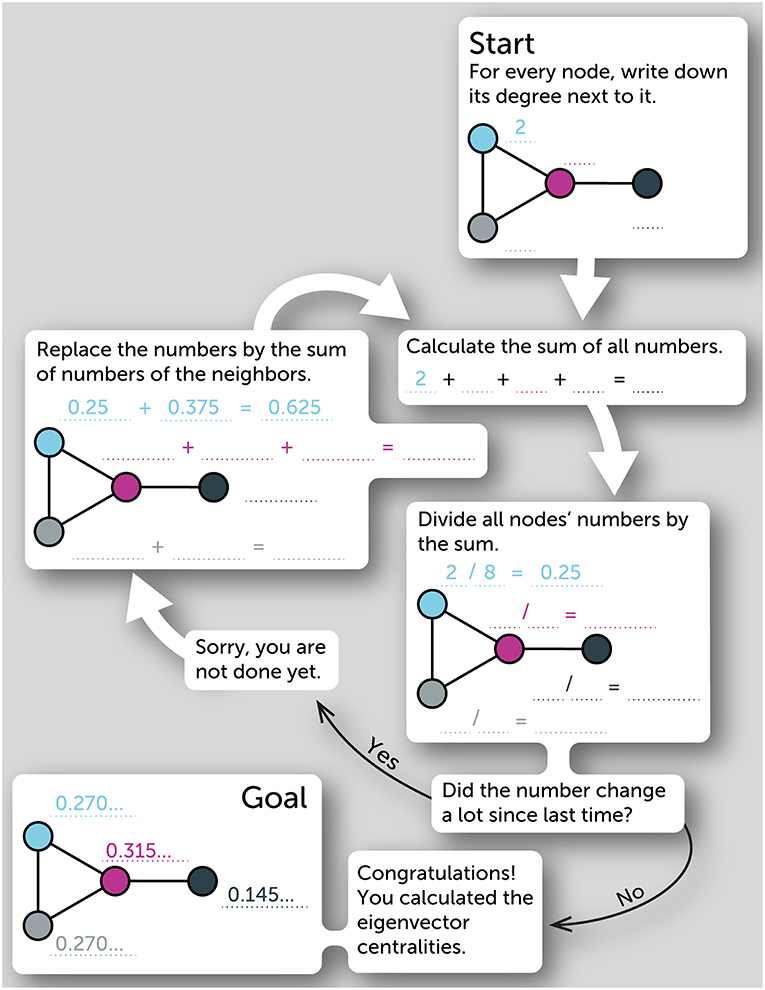
- איור 2 - תהליך של צעד אחר צעד לחישוב מרכזיות וקטור עצמי של הצמתים ברשת.
- הרשת הזו מראה מי מדבר עם מי בסרט. ככל ששתי דמויות מדברות יותר זו עם זו, כך הקו ביניהן עבה יותר. אנו מדגימים את התהליך הזה עם רשת פשוטה. אנו יכולים להשתמש בה כדרך אחת למדוד את החשיבויות של דמויות שונות בסרט לשבור את הקרח.
בשלב הזה אתם עשויים לתהות מדוע אנשים טורחים לחשב מספרים כמו מרכזיות וקטור עצמי כדי למדוד חשיבות. מצפייה בלשבור את הקרח ברור שמרבית הדברים קורים בגלל הקסם של אלזה, אז אולי היא צריכה להיות הדמות החשובה ביותר? אולם, התבוננו שוב ברשת באיור 1: זו רשת של אנשים שמדברים זה עם זה, לא של מי מבצע איזו פעולה שגורמת לאירוע מרכזי בסרט. הרשת באיור 1 מספרת לנו מי חשוב בסיפור הסרט לשבור את הקרח, יותר מאשר מי חשוב כגורם לאירועים עצמם בארנדל.
אנו יכולים לערוך חישוב דומה עבור רשת נרטיב, שהיא רשת של אלה אירועים גורמים לאירועים אחרים [1]. במקרה הזה, הרבה יותר קשה לבנות את הרשת. איור 3 הוא ניסיון להתחיל ליצור רשת כזו; אולי אתם תהיו מסוגלים להשלים אותה? ברשת כזו האירועים שנגרמים על-ידי אלזה עשויים להיות בעלי דרגות ומרכזיות וקטור עצמי גבוהות. זה אומר שאף על פי שאנה היא הדמות החשובה יותר עבור הסיפור של לשבור את הקרח, זו אלזה שהכי חשובה עבור האירועים שמרכיבים את הסיפור.
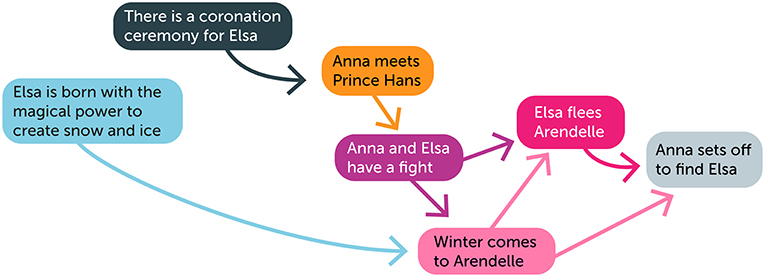
- איור 3 - נרטיב פשוט ולא שלם של רשת האירועים שלפני ההתחלה של לשבור את הקרח.
רשתות נמצאות בכל מקום
כעת משהדגמנו את הרעיון של חישוב מספרים כמו מרכזיות, בואו ניקח צעד אחורה. מדוע שיהיה לנו אכפת מהרשתות החברתיות והחישובים האלה? הסיבה היא שרשתות נמצאות בכל מקום בחיים שלנו, וחקירת הרשתות האלה מאפשרת לנו להבין מגוון רחב של דברים שונים [2, 3]. ניתן כמה דוגמאות.
דוגמה אחת חשובה מאוד של רשת היא האינטרנט. האינטרנט הוא רשת עולמית ענקית של מחשבים, טאבלטים, טלפונים ניידים ומכשירים אחרים שמחוברים על-ידי חוטים ודרך האוויר. אנו יכולים לחשוב על האינטרנט כמו רשת חברתית של מחשבים. לכל מחשב יש “חברים” (מחשבים אחרים שמחוברים אליו), והחברים האלה מרכיבים נתיבים לחלקים שונים ברשת, כמו ברשת החברתית של הדמויות בלשבור את הקרח. כשאתם שולחים הודעת טקסט מטלפון נייד, טאבלט או מחשב, היא מועברת הלאה לאחד החברים של המכשיר, לחבר של חברים שלו וכך הלאה, עד שבסופו של דבר ההודעה מגיעה למקבל (החבר שלכם). ידיעת התכונות של רשת המחשבים הענקית הזו חשובה מסיבות פרקטיות רבות. לדוגמה, מהנדסים רוצים לדעת אלה מכשירים חשובים יותר (מרכזיוּת) וכמה מכשירים בממוצע נדרשים כדי להגיע ממכשיר אחד לשני. ברשת גדולה כמו האינטרנט, האם ישנם צעדים רבים או מעטים לדעתכם [3]?
דוגמאות אחרות של רשתות הן אינטראקציות אקולוגיות בטבע. מינים ביולוגיים מְתַקְשְׁרִים זה עם זה בדרכים שונות רבות. אחת מהאינטראקציות החשובות ביותר היא מי אוכל את מי, מה שנקרא “טְרִיפָה”. אנו יכולים לבחור מין אחד (צפרדע, למשל) ולעשות רשימה של מינים אחרים שאוכלים אותו (למשל נחשים ורָקוּנים) ושהוא אוכל אותם (כמו זבובים ותולעים). אם אנו גם יוצרים את הרשימות האלה לכל אחד מהמינים, בסופו של דבר אנו מקבלים קבוצה גדולה של קשרים (שנקראת “רשת המזון”), אשר ממחישים את יחסי הטריפה בין מינים רבים שונים. זה די שונה מחברויות ומשיחות שדנו בהן קודם, אולם אנו יכולים ללמוד הרבה על אקולוגיה על-ידי חקירת סוג הרשת הזה. לדוגמה, המרכזיות של מינים עשויה להיות אינדיקציה לַמידה שבה היכחדות של מין מסוים יכולה לגרום לנזק אקולוגי.
הדוגמאות האלה ממחישות את הכוח של ייצוגים מתמטיים כמו רשתות. אנו יכולים להשתמש באותם הכלים המתמטיים לחקור הרבה רשתות שונות, אף על פי שרכיבים אמיתיים של רשת – כמו דמויות, מחשבים או מינים ביולוגיים – יכולים להיות שונים מאוד. ישנן הרבה דוגמאות אחרות של רשתות נוסף על אלה שדנו בהן כאן. האם אתם יכולים לחשוב על דוגמאות בעצמכם?
מה עוד אנו יכולים לחקור על רשתות?
בדוגמאות של רשתות שדנו בהן קודם, איננו נותנים לרשתות להשתנות אף על פי שאנשים יוצרים חברויות חדשות כל הזמן, כמו כשהם הולכים לבית ספר חדש. איננו מבחינים גם בין סוגים שונים של קשרים. בלשבור את הקרח, לדוגמה, אלזה ואנה הן אחיות, אולם אנה ואולף הם חברים.
כיום, מדענים חוקרים באופן אקטיבי דרכים להרחיב את החישובים למצבים מורכבים יותר, כמו למשל רשתות שבהן צמתים וחיבורים מתווספים, משתנים או מוּסָרִים במהלך הזמן [4]. בגלל שהרשת של מי מדבר עם מי בלשבור את הקרח מתפתחת עם הזמן עם התקדמות הסיפור, רצוי למדוד דמויות חשובות בדרכים שמאפשרות לחשיבויות להשתנות עם הזמן. סממן חשוב נוסף של רשתות חברתיות הוא שישנם הרבה סוגים של קשרים בבת אחת, לא רק חברויות; וחוקרים מפתחים באופן אקטיבי דרכים למדוד צמתים חשובים באופן שמשלב בין קשרים מרובים. זה מועיל לא רק לרשתות חברתיות אלא גם לסוגים אחרים של רשתות. בטבע, לדוגמה, חיות לא רק אוכלות זו את זו; הן גם מְתַקְשְׁרוֹת זו עם זו בדרכים שונות, והמבנים החברתיים המורכבים שלהן תלויים בקשרים המגוונים האלה [5].
חֵקֶר רשתות הוא תחום מחקר מרגש שמקשר בין רעיונות מתחומי המתמטיקה, מדעי החברה, פיזיקה, מדעי המחשב, אקולוגיה ונושאים רבים אחרים. בעיה אחת עיקרית בניתוח רשת היא קביעת הדרכים הטובות ביותר למדוד את חשיבותם של אנשים, חיות וישויות אחרות. דרך ההדגמה שלנו עם הסיפור של לשבור את הקרח, נתנו לכם חלון הצצה לתחום המחקר המרגש הזה.
מילון מונחים
רשת (Network): ↑ אוסף של צמתים והחיבורים שביניהם.
צומת (Node): ↑ הדברים ברשת שמחוברים לדברים אחרים. לדוגמה, ברשת החברתית של לשבור את הקרח הדמויות בסרט הן הצמתים.
דרגה (Degree): ↑ מספר השכנים של צומת.
שכנים (Neighbors): ↑ הצמתים שאליהם מחובר הצומת.
מרכזיוּת (Centrality): ↑ מספר שמבטא כמה צומת מסוים חשוב.
מרכזיות וקטור עצמי (Eigenvector Centrality): ↑ סוג של מרכזיות שבנוי על הרעיון שלצמתים חשובים יש שכנים חשובים.
הצהרת ניגוד אינטרסים
המחברים מצהירים כי המחקר נערך בהעדר כל קשר מסחרי או פיננסי שיכול להתפרש כניגוד אינטרסים פוטנציאלי.
תודות
אנו אסירי תודה ל-Nia Chiou, Maria Chrysafis, Ana Gershenson, Anthony Jin, Veda Montgomery, Martha New, Kate Van Hooser ו-Austin Wu עבור הערותיהם המועילות מאוד על טיוטת המאמר הזה. אנו מודים גם להורים ולמורים שלהם - Lyndie Chiou, Christina Chow, Carlos Gershenson, Marlon Montgomery, Steve New ו-Steve Van Hooser עבור הקישור בינינו והפצרה לקבל מהם משוב. אנו מודים לשני הסוקרים והמנטורים המדעיים שלהם על ההערות הבונות ויקרות הערך שלהם. לבסוף אנו מודים ל-Susan Debad על עריכה זהירה של כתב היד שלנו במטרה לגרום לו להיות נגיש יותר לקהל הצעיר שלנו.
מקורות
[1] ↑ Bearman, P., Moody, J., and Faris, R. 2003. Networks and history. Complexity 8:61–71. doi: 10.1002/cplx.10054
[2] ↑ NetSciEd. (Eds). 2015. Network Literacy: Essential Concepts and Core Ideas. Available online at: http://tinyurl.com/networkliteracy (Accessed 5 July, 2019)
[3] ↑ Newman, M. E. J. 2018. Networks, 2nd Edn. Oxford: Oxford University Press.
[4] ↑ Taylor, D., Myers, S. A., Clauset, A., Porter, M. A., and Mucha, P. J. 2017. Eigenvector-based centrality measures for temporal networks. Multiscale Model. Simul. 15:537–74. doi: 10.1137/16M1066142
[5] ↑ Finn, K. R., Silk, M. J., Porter, M. A., and Pinter-Wollman, N. 2019. The use of multilayer network analysis in animal behaviour. Anim. Behav. 149:7–22. doi: 10.1016/j.anbehav.2018.12.016