רעיון מרכזי מתמטיקה וכלכלה פורסם: 23 באפריל, 2025

למצוא את הדרך: מהו הנתיב הקצר ביותר ברשתות?

תַקצִיר

נסיעות ליעדים שונים הן חלק משמעותי בחיינו. אנו מבקרים במִּגוון מקומות, הן בחיי היומיום שלנו והן כשאנו בחופשה. כיצד באפשרותנו למצוא את הדרך המיטבית לנווט ממקום אחד לאחר? אומנם אנו יכולים לבחון את כל הדרכים השונות המְּחברות בין שני המקומות, אך שיטה אחרת היא להשתמש במתמטיקה ובחִשּׁוּבים כדי למצוא את המסלול הקצר ביותר ביניהם. במאמר זה, נדון בדרכים לבניית הנתיבים הקצרים ביותר, ונציג את אלגוריתם דייקסטרה (Dijkstra), המשמש לצמצום העלוּת הכוללת של מסלול מסוים. העלות מורכבת ממרחק הנסיעה, מזמן הנסיעה או מאַמַּת מידה אחרת. נדון גם בדרך שבה ניתן להשתמש במסלולים הקצרים ביותר בעולם האמיתי כדי לחסוך זמן ולייעל את המסע.

מהו מסלול?

מִדֵּי יום, אנו מחליטים באלה מסלולים להשתמש כדי לנוע בין מקומות שונים. בבית, אתם עשויים לעבור מחדר השינה אל המטבח. מחוץ לבית, אתם עשויים לעבור בין הבית לבית הספר. נניח שיש לנו רשת של מקומות, המחוברים זה לזה באמצעות רחובות ושבילים. כל אחד מהמקומות הללו מכונה צומת (או קודקוד), והרחובות והשבילים מכונים קשתות (מונח בתורת הגרפים). ה’שכנים’ של צומת מסוים הם הצמתים המחוברים אליו באמצעות קשת. מסלול הוא רֶצֶף של קשתות בין צומת המקור לצומת היעד [1, 2].

המסלולים הקצרים ביותר

במתמטיקה, חוקרים בוחנים את אורכי המסלולים כדי לבנות מסלולים קצרים. לעיתים קרובות ישנהּ תועלת במציאת המסלול הקצר ביותר. זהו מסלול בין שני צמתים, שבו מִספר הקשתות הוא המועט ביותר, אם העלות של תנועה לאורך כל קשת זהה (לדוגמה, אם כל קשת הוא רחוב באותו האורך). באופן כללי יותר, בהינתן צומת מקור וצומת יעד, מסלול קצר ביותר ביניהם הוא זה אשר לו העלות הכוללת הנמוכה ביותר מבּין כל המסלולים האפשריים מהמקור אל היעד [1]. כדי לחשֵּׁב את עלות המסלול, עָלֵינו לסכֹּם את העלויות הפרטניות של כל אחת מהקשתות שבו. ניתן למדוד עלות במרחק, בזמן או במדד אחר. לדוגמה, במפת העיר הקטנה שבאיור 1, מסלול קצר ביותר מהבית אל בית הספר עשוי להיות זה שהתנועה בו אורכת הכי מעט זמן מבּין המסלולים האפשריים. בין שני צמתים ברשת נתונה עשוי להיות יותר ממסלול אחד שהוא הקצר ביותר, כיוון שלכמה מסלולים עשויה להיות אותה עלות מינימלית. לכן אנו מתייחסים אליו בתור ’אחד המסלולים הקצרים ביותר’ בין שני צמתים (למרות שזה נשמע מוזר), ולא בתור ’המסלול הקצר ביותר’ ביניהם.

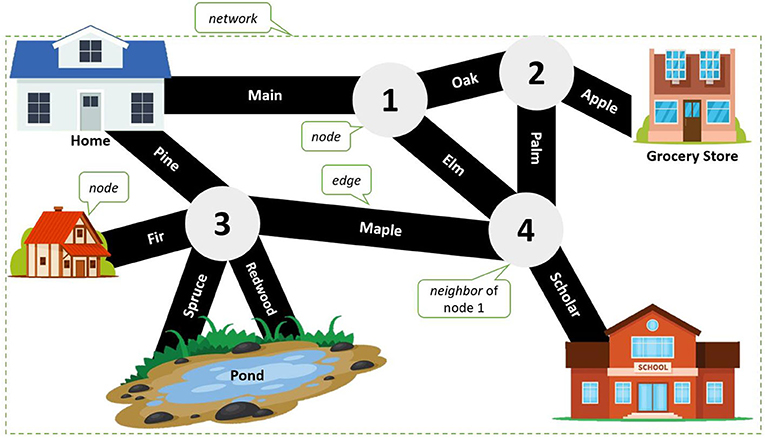
איור 1 - אתגר בחירת מסלולים.
  • איור 1 - אתגר בחירת מסלולים.
  • במפת העיר הקטנה הזו, המהווה דוגמה לרשת ,(network) מקומות (כלומר, צמתים) 4-1 נמצאים על הצמתים (node) בין הרחובות (שהם הגבולות המחבּרים - edge). כל אחד מהמקומות הללו (הבתים - Home הכחול והאדום, הבריכה הקטנה - Pond, בית הספר - School, וחנות המכולת - Grocery store), גם הם צמתים. פעילות 1: הַתְווּ מסלול מהבית הכחול אל בית הספר על המפה. באֵילו רחובות (כלומר, קשתות) באיור תבחרו? באיזה מסלול אתם בוחרים כדי להגיע מהבית אל בית הספר בחיים האמיתיים? (ההשראה לאיור זה נלקחה מהתמונה בקישור http://clipart-library.com/clipart/449476.htm. באיור נעשה שימוש גם באוסף תמונות ציבורי). מקרא: edge = קשת; neighbor of node 1 = בשכנות לצומת 1; הרחובות, המסומנים בשחור, נושאים שמות של עצים שונים.

אתם כבר ודאי חושבים על מסלולים קצרים ביותר בחיי היומיום, שמובילים אתכם למקומות שונים. בדוגמת חדר השינה-מטבח שהבאנו קודם, לא הגיוני ללכת מחדר השינה לחדר הכביסה, לאחר מכן לצאת החוצה לחצר האחורית, ולהגיע לבסוף למטבח, אם אתם רוצים בסך הכול לעבור מחדר השינה למטבח. יהיה הרבה יותר מהיר ללכת ישירות מחדר השינה למטבח, בלי לעצור בדרך בחדר הכביסה ובחצר האחורית. במסע בין מקומות הקרובים זה לזה, יש רק כמה צמתי רחובות (כלומר, צמתים), ואולי תצליחו לבדוק את רוב המסלולים השונים כדי לאתֵּר מסלול קצר ביותר. אך אם המקומות הללו רחוקים יותר – לדוגמה, ביתכם, בית הספר שלכם וחנות צעצועים בעיר אחרת – יהיה הרבה יותר קשה למצוא מסלול קצר ביותר. כיצד אמצעֵי ניווט כמו ’גוּגל מפות’ קובעים את הדרך המיטבית להגיע ליעד מסוים? אחת האפשרויות היא לפתור את בעיית המסלול הקצר ביותר. זוהי בעיה מתמטית העוסקת במציאת המסלול בין שני צמתים בצורה שמצמצמת את סכום העלויות של הקשתות במסלול1.

במתמטיקה, לעיתים קרובות אנו מסמנים צמתים כמִּספרים (רְאו הצמתים באיור 1), או כאותיות (רְאו איור 2). כדי לפשֵּׁט את הדברים, אנו גם מניחים שהכול דו-ממדי (כמו תרשים על פיסת נייר), כך שנוכל למדוד מרחק בדרך שבה אנו מודדים אותו בין שתי נקודות על רצפת הבית. איננו מביאים בחשבון משתנים כמו גובה, או קימור כדור הארץ. ברשת שבאיור 2, אם אנו רוצים למצוא את אחד המסלולים הקצרים ביותר מצומת A לצומת F, עלֵינו לבחור בקשתות בעלוֹת העלויות הנמוכות ביותר. לדוגמה, בּמְקום לבחור בקשת בעלוּת 4 מצומת A לצומת B, נבחר בקשת שעלותהּ 2 מצומת A לצומת C. בחירת הקשתות בעלוֹת העלויות הנמוכות ביותר כדי למצוא מסלול קצר ביותר, היא אחד מרעיונות המפתֵּח באלגוריתם דייקסטרה2,3.

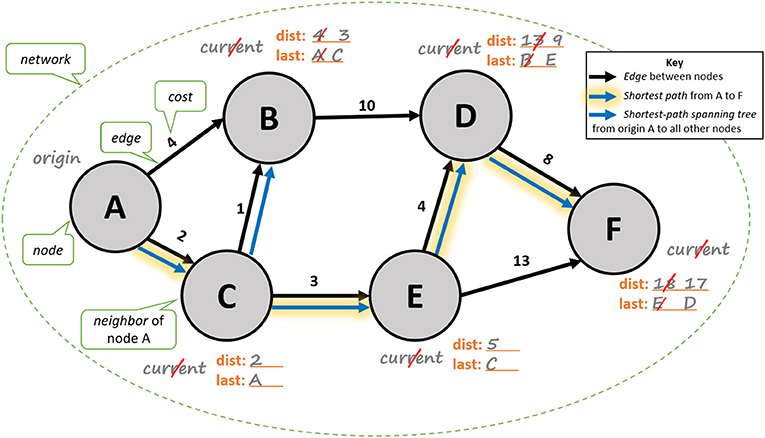
איור 2 - בחירה בנתיבים הקצרים ביותר.
  • איור 2 - בחירה בנתיבים הקצרים ביותר.
  • ברשת (network) הזו, החיצים הכחולים המודגשים מראים לנו מהו המסלול הקצר ביותר מצומת A לצומת F. המִּספרים מצביעים על עלויות (cost) הקשתות (שאינם מצוירים לפי קנה המידה). החיצים הכחולים מציגים את פרישׂת עץ הנתיבים הקצרים ביותר, כאשר A הוא צומת המקור (origin). שימו לב לכך שהמסלול מצומת A לצומת F מהווה חלק מפרישׂת עץ הנתיבים הקצרים ביותר. התווית ‘dist’ מתייחסת למרחק הכולל מצומת ה’מקור’ אל צומת מסוים, והתווית ’last’ מתייחסת לצומת האחרון שבו עברנו כדי להגיע לצומת יעד מסוים מה’מקור’ A. בפסקה הבאה במאמר, שכותרתה ’אלגוריתם דייקסטרה’, אנו מְספּקים הסבר מפורט לגבי הצעדים הנדרשים לקביעת מסלול קצר ביותר [ההשראה לאיור זה נלקחה מאיורים המצויים ברשת]1,3.

אלגוריתם דייקסטרה

’אלגוריתם’ הוא מַעֲרָךְ מדויק של צעדים שצריך לבצע כדי לפתור בעיה, כמו בעיית המסלול הקצר ביותר [1]. אלגוריתם דייקסטרה הוא אלגוריתם מפורסם למציאת אחד המסלולים הקצרים ביותר. הוא נקרא על שמו של ממציאו, אֶדְסְחֶר דֶיְיקְסְטְרָה, שהיה מדען מחשבים הולנדי מוכר4. אחד השימושים של אלגוריתם דייקסטרה הוא יצירה של פרישׂת עץ הנתיבים הקצרים ביותר (ראו איור 3). מטרת הפרישׂה היא למצוא מסלול קצר ביותר בין צומת מקור לכל צומת אחר ברשת, זאת על ידי חישוב בנפרד של המרחק מצומת המקור אל כל אחד מהצמתים האחרים. בדיון שלנו, העלות נמדדת במרחק, אך ניתן להשתמש באלגוריתם דייקסטרה עבור כל סוג של עלות.

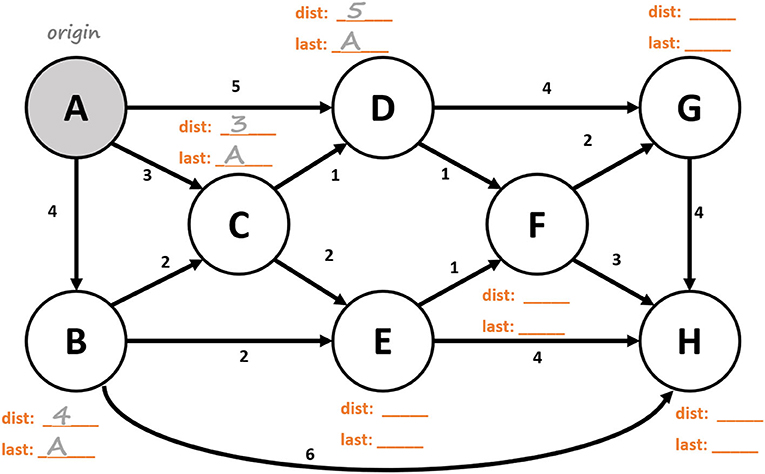
איור 3 - עכשיו תורכם! פעילות 2: השתמשו באלגוריתם דייקסטרה כדי למצוא פרישׂת עץ נתיבים קצרים ביותר מהמקור אל כל צומת אחר ברשת הזו5.
  • איור 3 - עכשיו תורכם! פעילות 2: השתמשו באלגוריתם דייקסטרה כדי למצוא פרישׂת עץ נתיבים קצרים ביותר מהמקור אל כל צומת אחר ברשת הזו5.
  • השלמנו עבורכם את השלב הראשון של אלגוריתם דייקסטרה [ההשראה לאיור זה נלקחה מפעילות המצויה ברשת1].

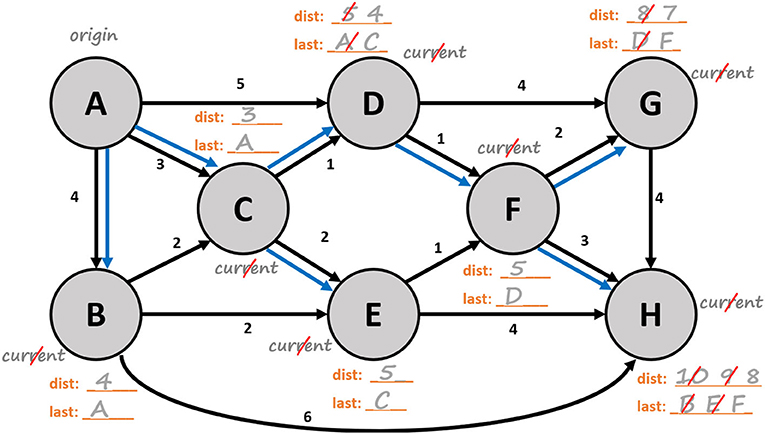
באיור 2, אנו מראים כיצד להשתמש באלגוריתם דייקסטרה כדי לבנות פרישׂת עץ נתיבים קצרים ביותר עבור רשת מחוברת. עִקבו אחר איור 2 בעוד אתם קוראים את ההסבר, וצְפו בסרטון 1 המציג הַנְפָּשָׁה של דוגמה זו.

  • בסרטון 1 - מקרא: : edge = קשת; node = צומת; neighbor of node A = בשכנוּת לצומת A; current = הצומת הנוכחי.
  • בתבנית המלבנית מצד ימין, לפי סדר החיצים מלמעלה למטה: קשת בין צמתים; הנתיב הקצר ביותר בין A ל-F; פרישׂת עץ נתיבים קצר ביותר מהמקור ב-A לכל הצמתים האחרים.

הסבר לאיור 2: עקבו אחר ההסבר המופיע בסרטון, לדוגמה של שימוש באלגוריתם דייקסטרה למציאת פרישת עץ הנתיבים הקצרים ביותר עבור הרשת באיור 2.

הנה הצעדים שאנו מְבצעים:

1. ’נמלֵּא’ (בְּצֶבַע) את צומת ה’מקור’ (רְאו צומת A באיור 2). עבור כל שָׁכֵן של צומת ה’מקור’, נקבע את הָעֵרֶךְ ההתחלתי של dist (מרחק) בתור המרחק מצומת ה’מקור’ אל אותו שכן, ואת הערך ההתחלתי של last (אחרון) כצומת ה’מקור’. בדוגמה שבאיור 2, בסוף הצעד הזה, נמלא את הערכים ל-dist ול-last, עבור הצמתים B ו-C. רשומות ה-dist וה-last עבור צמתים D, E ו-F עדיין ריקות.

2. נזהה את הצומת ה’ריק’ (מִצֶּבַע) בעל ערך ה-dist הנמוך ביותר (לא נכלול את אלו שאין להם ערך), ונתייג אותו כצומת ה’נוכחי’ שלנו. לדוגמה, אם אנו מתחילים עם צומת A כצומת ה’מקור’, הצומת ה’נוכחי’ הוא צומת C, כיוון שערך ה-dist בין A ל-C נמוך מערך ה-dist בין A ל-B. אם ערכי המרחק שווים, נבחר באחד מבּין הצמתים בעלי ערך ה-dist הנמוך ביותר.

3. נבצע את השלבים הבאים עבור כל אחד מהשכנים ה’ריקים’ של הצומת ה’נוכחי’:

a. נוסיף את ערך ה-dist של הצומת ה’נוכחי’ לעלוּת הקשת מהצומת ה’נוכחי’ לשכן.

b. אם ערך ה-dist משלב 3א קטן מערך ה-dist של השכן (או אם ערך ה-dist של השכן עדיין חסר), נעדכן את ערך ה-dist של השכן לערך ה-dist שחישבנו בשלב 3א, ונקבע את ערך של השכן כצומת ה’נוכחי’.

4. לאחר שנשלים את שלב 3 עבור כל השכנים ה’ריקים’ של הצומת ה’נוכחי’, ’נמלא’ (בצבע) את הצומת ה’נוכחי’ ונמחק את תיוג ה’נוכחי’.

5. אם כל הצמתים ’מלאים’, אנו ממשיכים לשלב אחרת, אנו חוזרים לשלב 2.

6. נדגיש את הקשת בין כל צומת לצומת שלו, כדי לחשוף פרישׂת עץ נתיבים קצרים ביותר מה’מקור’.

יישׂומים

בעזרת אלגוריתם דייקסטרה, באפשרותנו למצוא מסלול קצר ביותר מצומת המקור אל כל צומת אחר ברשת. אם תחשבו על ביתכם כצומת המקור, ועל היעד שלכם ככמה צמתים אפשריים ברשת, תוכלו למצוא נתיב טוב מהבית אל כל מקום שאליו תרצו להגיע. נניח שתרצו לבקֵּר בכמה מקומות לפני שאתם חוזרים הביתה. כיצד תמצאו את הדרך המיטבית לבקר בכל היעדים הללו תוך חיסכון בזמן וצמצום הוצאות כמו דלק ומלונות? באופן מופשט יותר, כיצד ביכולתנו למצוא מסלול קצר ביותר שעובר בכל הצמתים ברשת וחוזר אל הצומת ההתחלתי? בעיה זו, שהיא הרחבה של בעיית המסלול הקצר ביותר, ידועה כ’בעיית איש המכירות הנודד’6.

מציאת מסלולים קצרים ביותר חשובה לפתרון בעיות במגוון סוגי רשתות. לדוגמה, מסלולים קצרים ביותר עשויים לשפר את יעילוּת התכנון של עיר. מהנדסים אזרחיים יכולים ליצור ייצוג של עיר כרשת, ולקבוע מָהֵם המקומות המיטביים לבניית דרכים שיפחיתו את עומס התנועה, ומָהֵם המקומות המיטביים לצינורות שתייה שיְּסַפּקוּ מים לתושבים [2]. מציאת מסלולים קצרים ביותר גם מאפשרת להעביר נתונים ממחשב אחד לאחר במהירות גבוהה, מה שמאפשר זרימת כמויות מידע עצומות בתוך שניות [1, 2].

ישנן גם דוגמאות רבות של מסלולים קצרים בתקשורת וברשתות חברתיות. לדוגמה, נניח שכָּל אדם ברשת חברתית הוא צומת, ושכָּל קשת מייצגת חברוּת. תוכלו להבין איך ליצור קשר עם אדם שנמצא מחוץ לקבוצות החברים שלכם, דרך קשריהם של חבריכם. המסלולים הקצרים ביותר של קשרים (כמו חברויות), בין שני אנשים אקראיים בארה“ב עשויים להיות קצרים יותר משאתם מְשַׁעֲרִים. בממוצע, במסלול כזה יש פחות משישה שלבים בין אדם ה’מקור’ לאדם ה’יעד’ [3]! מסלולים קצרים בין אנשים ממחישׁים את ’תופעת העולם הקטן’, ואורכי המסלולים הקצרים הללו הם גם אלה שהיוו השראה למונח ’שש דרגות של הפרדה’ (רעיון במדעי החברה שלפיו כל שני אנשים בעולם מקושרים על ידי חמישה אנשים אחרים, לכל היותר) [1].

דוגמה נוספת מתייחסת לאירועים עכשוויים. במהלך מגפת נגיף הקורונה (קוֹבִיד-19), מציאת מסלולים קצרים הייתה יעילה להגבלת החשיפה לנגיף שגורם למחלה. בתקופה זו הרווחנו מחישוב מסלול קצר בשעה שערכנו קניות במרכּוֹל ואספנו מוצרים. זאת תוך שאנו נמנעים ממגע עם אנשים אחרים על ידי שמירת מרחק פיזי [4, 5].

סיכום

למציאת מסלולים קצרים ביותר נודעת חשיבוּת כדי להגיע ממקום אחד למקום אחר. למסלולים אלה יישׂומים רבים במגוון סוגי רשתות, וביכולתם לסייע לפתור מגוון בעיות בעולם האמיתי. מתכנון חופשה משפחתית ועד לגילוי הקְּשרים בעולמנו, מחקר מסלולים קצרים ביותר ברשתות הוא בעל חשיבות מכרעת, ומהווה בסיס למחקרים מורכבים יותר.

מילון מונחים

רשת (Network): ↑ אוסף של פריטים (אובייקטים, המכונים ’צמתים’) והחיבורים ביניהם (המכונים ’קשתות’).

צומת (Node): ↑ פריטים (אובייקטים) ברשת המחוברים לפריטים אחרים. לדוגמה, באיור 1, כל מיקום וכל צומת רחוב מהווים צומת.

קשת (Edge): ↑ פריט (אובייקט) המחבּר שני צמתים זה לזה. לדוגמה, כאשר אתם נעים מהבית לבית הספר, כל רחוב הוא קשת.

מסלול (Path): ↑ רֶצֶף של קשתות מצומת המקור לצומת היעד.

עלות (Cost): ↑ מידת המאמץ הנדרשת כדי לנוע לאורך קשת בתוך רשת. בחיים האמיתיים, עלות עשויה להימדד במרחק, בזמן, או במדד אחר.

מסלול קצר ביותר (Shortest Path): ↑ נתיב שמוביל מצומת המקור אל צומת היעד, שהוא בעל העלות הכוללת הנמוכה ביותר מבּין כל הנתיבים מהמקור אל היעד.

פרישׂת עץ נתיבים קצרים ביותר (Shortest-path Spanning Tree): ↑ חלק מרשת מחוברת שמתחיל מצומת מקור מסוים ומְפרט מסלול קצר ביותר מצומת זה לכל צומת אחר ברשת. לדוגמה, אם ברשת 6 צמתים, ישנם 5 מסלולים קצרים ביותר כאלה בעץ פרישׂת מסלולים קצרים ביותר. עץ כזה של רשת כולל את כל הצמתים שברשת. נוסף על כך, כיוון שעץ כזה הוא סוג רשת הידועה כ’עץ’, לכל זוג צמתים ברשת ישנוֹ בדיוק נתיב אחד המחבּר ביניהם.

הצהרת ניגוד אינטרסים

המחברים מצהירים כל המחקר נערך בהעדר כי קשר מסחרי או פיננסי שיכול להתפרש כניגוד אינטרסים פוטנציאלי.

תודות

אנו מודים לקוראים הצעירים שלנו – Nia Chiou, Taryn Chiou, Zoë Chiou, Tycho Elling ו- Sage Hansen– עבור הערותיהם המועילות הרבּות. אנו מודים גם לבני משפחותיהם – Tim Elling, Christina Chow, Lyndie Chiou ו- Sterling Hansen – על כך שחיברו בינינו, ועזרו לנו לקבל מהם משוֹב. נוסף על כך ברצוננו להודות ל- Michelle Lee, Lyndie Chiou, Thomas Rexin ו-Akrati Saxena עבור הערותיהם המועילות, וכן לסוקרים הצעירים שלנו ולמנחים שלהם עבור הצעותיהם המצוינוֹת הרבּות. MAP מודה על התמיכה מטעם הקרן הלאומית למדע (NSF, ארה”ב) – מענק מספר 1922952, באמצעות תוכנית האלגוריתמים לזיהוי אִיּוּמִים (ATD).

מקורות

[1] ↑ Newman, M. E. J. 2018. Networks, 2nd Edn. Oxford, UK: Oxford University Press.

[2] ↑ Cramer, C., Porter, M. A., Sayama, H., Sheetz, L., and Uzzo, S. (eds). 2015. Network Literacy: Essential Concepts and Core Ideas. Available online at: http://tinyurl.com/networkliteracy

[3] ↑ Milgram, S. 1967. The small-world problem. Psychol Today 1:61–7. doi: 10.1037/e400002009-005

[4] ↑ Brooks, H. Z., Kanjanasaratool, U., Kureh, Y. H., and Porter, M. A. 2021. Disease detectives: Using mathematics to forecast the spread of infectious diseases. Front. Young Minds 9:577741. doi: 10.3389/frym.2020.577741

[5] ↑ Ying, F., and O’Clery, N. 2021. Modelling COVID-19 transmission in supermarkets using an agent-based model. PLoS ONE 16:e0249821. doi: 10.1371/journal.pone.0249821

נספח

מפתח תשובות

פעילות 1: מסלול אפשרי אחד הוא )Main - ראשי, Elm - בּוּקִיצָה, Scholar - תלמיד). מסלול אפשרי נוסף הוא )Main - ראשי, Oak - אלון, Palm - דקל, Scholar - תלמיד). מסלול אפשרי שלישי הוא (Pine - אורן, Maple - אֶדֶר, Scholar - תלמיד).

פעילות 2: הנה דוגמה אחת לפרישׂת עץ נתיבים קצרים ביותר שלמה עבור הרשת באיור 3. עִקבו אחר ההסבר בסרטון 2.

לחצו כאן לצפייה בסרטון 2.

הערות שוליים

[1] ↑ ויקיפדיה. 2020. בעיית המסלול הקצר ביותר. זמין ברשת בכתובת: https://en.wikipedia.org/wiki/Shortest_path_problem (נפתח לגישה ב-20 באוגוסט, 2020).

[2] ↑ בהגייה של השם ,Dijkstra ה-J היא שקטה.

[3] ↑ Code.org. .2020 מדריך פעילות U2L07 – אלגוריתם מסלול קצר ביותר של דייקסטרה. זמין ברשת בכתובת: https://docs.google.com/document/d/15N7aHAoWG1\_9VIcDHNZRygzFK0hle-EHlmHu0PZI8D4/view (נפתח לגישה ב-20 באוגוסט, 2020).

[4] ↑ ויקיפדיה. 2020. Edsger W. Dijkstra. זמין ברשת בכתובת: https://en.wikipedia.org/wiki/Edsger\_W.\_Dijkstra (נפתח לגישה ב-20 באוגוסט, 2020).

[5] ↑ ניתן להוריד גרסה להדפסה של איור3 – איור 3 בכתובת https://drive.google.com/file/d/1rNONK-cmy4gq_aCJRnAYpe9Y2HSeq2A1/view.

[6] ↑ רְאו https://www.youtube.com/watch?v=q8nQTNvCrjE\&t=35s.