ملخص
يُعد السفر إلى وجهاتٍ مُختلفةٍ جزءًا مهمًا في حياتنا. إذ إننا نزور أماكن عديدة خلال حياتنا اليومية وفي خلال فترات العُطلة. فكيف يُمكننا العثور على الطريقة المُثلى للتنقل من مكان إلى آخر؟ رُبما يُمكننا تجربة جميع الطرق المُختلفة للتنقل بين مكانين، ولكن توجد طريقة أخرى تقوم على الرياضيات والإحصاء؛ للعثور على أقصر طريق بينهما. وفي هذا المقال، سنُناقش كيفية استنتاج أقصر الطُرُق، وشرح خوارزمية ديكسترا؛ لخفض إجمالي تكلفة أحد المسارات. وقد تكون التكلفة هي مسافة السفر أو وقته أو أمثلة أخرى. كما سنُناقش كيفية الاستفادة من أقصر الطرق للحفاظ على الوقت وزيادة جودة السفر.
ما المقصود بالمسار؟
نتخذ قرارات حول الطُرُق التي سنسلكها للتنقل بين الأماكن المُختلفة يوميًّا. وقد تتنقل في منزلك بين غرفة نومك والمطبخ.
وفي الخارج، قد تتنقل من منزلك إلى المدرسة. لذا، لنفترض أن لدينا شبكة من الأماكن التي ترتبط ببعضها البعض عبر الشوارع والممرات. ويُعرف كل مكان من هذه الأماكن باسم العقدة، وتُعرف الشوارع والممرات باسم الحواف. كما أن ''جيران'' العُقدة هم العقد التي تتصل بالحافة. لذا، فالمسار هو سلسلة من الحواف المُمتدة من عقدة البداية إلى عقدة الوجهة [1, 2].
المسارات الأقصر
يُستخدم علم الرياضيات لدراسة أطوال المسارات بغرض استنتاج المسارات الأقصر. وغالبًا ما يكون مُفيدًا في العثور على المسار الأقصر. ويُعرف المسار الأقصر بأنه المسار الموجود بين عُقدتين تمتلكان أقل عددٍ من الحوافِ، في حال تساوي تكلفة التنقل على طول كل حافة (على سبيل المثال، إذا كانت كل حافة شارعًا له نفس الطول). وبعبارة أعم، بالنظر إلى العقدة الأصلية وعقدة الوجهة، يُعدُ المسار الأقصر المُمتد من عقدة البداية إلى عقدة النهاية هو المسار الأقل تكلفة إجمالًا بين جميع المسارات الموجودة من البداية حتى الوجهة [1]. ولحساب تكلفة المسار، يجمع الشخص تكاليف كل حافة على حدة. ويُمكن استخدام التكلفة لقياس المسافة، أو الوقت، أو أي عامل آخر. على سبيل المثال، في خريطة المدينة الصغيرة في الشكل 1، يُمكن أن يكون المسار الأقصر من المنزل حتى المدرسة هو الطريق الذي يُمكن اجتيازه في أقل وقت من بين المسارات المُتاحة. ومن المُمكن تواجد أكثر من مسار قصير بين عقدتين في الشبكة؛ لاحتمالية امتلاك المسارات المتعددة الحد الأدنى ذاته من التكلفة. ولهذا السبب، نقول ''أحد'' أقصر المسارات بين عقدتين (حتى وإن بدا ذلك غريبًا)، بدلًا من أن نقول ''أقصر'' مسار بينهما.
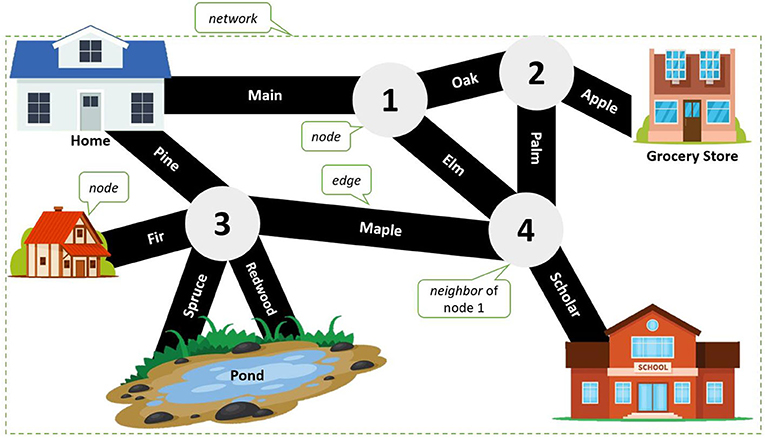
- شكل 1 - في خريطة المدينة الصغيرة هذه، والتي تُحاكي الشبكة، توجد الأماكن من 1 إلى 4 (العُقَد) عند تقاطعات الطُرُق (الحواف).
- وتُعدُ جميع الأماكن (المنازل الزرقاء والحمراء، والبركة، والمدرسة، والبقالة) نقاطًا للتلاقي. النشاط :1 تتبع أحد مسارات الخريطة التي تربط بين المنزل الأزرق والمدرسة. ما الطرق (الحواف) التي ستسلُكَها في الصورة؟ وما الطُرُق التي تسلكها عند التنقل بين منزلك والمدرسة في حياتك اليومية؟ (هذا الشكل مُستوحى من الشكل الموجود عبر الرابط: http://clipart-library.com/clipart/449476.htm ويستخدم شكلنا قصاصة فنية عامة).
ومن المُرجح أنك تُفكر بالفعل في المسارات الأقصر في حياتك اليومية عند ذهابك للأماكن المُختلفة. ففي مثالنا الذي طرحناه سابقًا عن التنقل من غرفة النوم إلى المطبخ، لن يكون منطقيًّا أن تسير من غرفة نومك، ثم إلى غرفة الغسيل، ثم تخرج إلى الفناء الخلفي لمنزلك، ثم تتجه أخيرًا إلى مطبخك، إذا أردتَ الانتقال من غرفة نومك إلى مطبخك.
سيكون من الأسرع السير مُباشرةً من غرفة نومك إلى مطبخك، دون التوقف أولًا في غرفة الغسيل والفناء الخلفي لمنزلك. وعند التنقل بين أماكن قريبة من بعضها البعض، لا تجد سوى القليل من تقاطعات الطرق (العُقد)، وربما يُمكنك تجربة معظم المسارات المُختلفة؛ للعثور على المسار الأقصر. ولكن إذا كانت الأماكن بعيدة عن بعضها البعض - على سبيل المثال، أن يقع منزلك، ومدرستك، ومتجر الألعاب في مدن مختلفة - فسيصعُب كثيرًا العثور على المسار الأقصر. والسؤال هنا: كيف تُحدد أدوات الملاحة؛ مثل خرائط جوجل، أفضل طريق للوصول إلى الوجهة؟ يُمثل حل مسألة المسار الأقصر إحدى هذه الطُرُق، وهي المسألة الرياضية المُتمثلة في تحديد مسار بين عقدتين بطريقة تُقلل مجموع تكاليف الحواف الموجودة في المسار1.
في الرياضيات، كثيرًا ما نُميز العقد باستخدام الأرقام (انظر تقاطعات الطُرُق في الشكل 1)، أو الحروف (انظر الشكل 2). وللتبسيط، نفترض أن جميع الأشياء تحتوي على بُعدين (كما هو الحال في الرسم على قطعة من الورق)؛ لذلك سنقيس المسافة بالطريقة التي تُقاس بها المسافة الموجودة بين نقطتين على أرضية منزلك. ولن نقلق حيال أشياء مثل ارتفاع، أو انحناء الأرض. وفي الشبكة الموجودة في الشكل 2، إذا أردنا العثور على المسار الأقصر المُمتد من العقدة A إلى العقدة ،F فينبغي أن نختار الحواف ذات التكلفة الأقل. وعلى سبيل المثال، نختار الحافة ذات التكلفة 2 المُمتدة من العقدة A إلى العقدة ،C بدلًا من اختيار الحافة ذات التكلفة 4 والمُمتدة من العقدة A إلى العقدة .C إذ يُعدُ اختيار الحواف ذات التكلفة الأقل للعثور على المسار الأقصر، إحدى الأفكار الرئيسية في خوارزمية ديكسترا (Dijkstra)2 ,3.
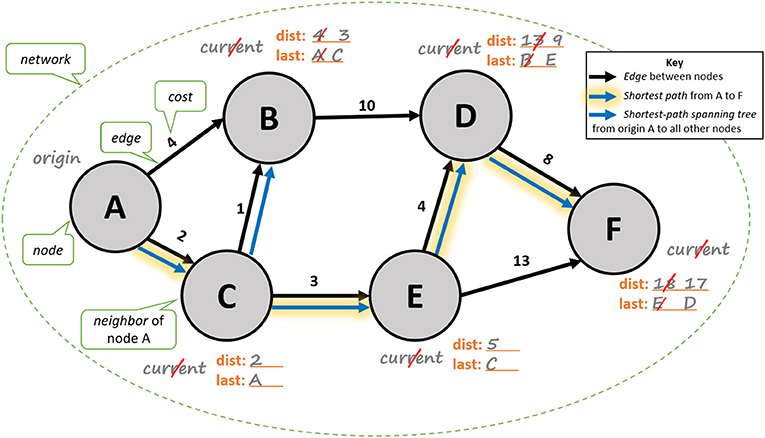
- شكل 2 - في هذه الشبكة، يُظهر لنا تتبُع الأسهم الزرقاء المسار الأقصر المُمتد من العقدة A إلى العقدة F.
- وتُشير الأعداد إلى تكلفة الحواف (لم يُشر إليها في مقياس الرسم). وتُظهر الأسهم الزرقاء ما يعرف بـ''شجرة امتداد المسار الأقصر''، التي تبدأ بالعقدة A. لاحظ أن أقصر مسار من العقدة A إلى العقدة F هو جزء من شجرة المسار الأقصر. وتُشير كلمة ''dist'' إلى المسافة الإجمالية من عقدة ''البداية'' إلى عقدة بعينها، وتُشير كلمة ''last'' إلى العقدة الأخيرة التي يمر بها الشخص؛ للوصول إلى عقدة وجهة بعينها، بدايةً من العقدة A. سنشرح بالتفصيل الخطوات اللازمة لتحديد المسار الأقصر في القسم المُسمى ''خوارزمية ديكسترا''. [هذا الشكل مُستوحى من الأشكال المُتاحة على الإنترنت1,3].
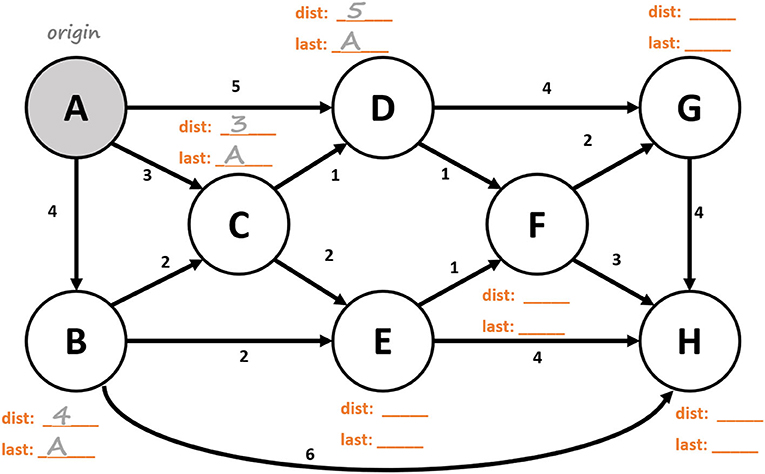
- شكل 3 - النشاط 2: حان دورك الآن! استخدم خوارزمية ديسكترا؛ للعثور على شجرة امتداد المسار الأقصر المُمتدة من عقدة البداية إلى العُقد الأخرى الموجودة في هذه الشبكة5.
- إذ أننا قد أنجزنا الخطوة 1 من خوارزمية Algorithm من أجلك. [هذا الشكل مستوحى من نشاطٍ مُتاحٍ عبر الإنترنت1].
خوارزمية ديكسترا
''الخوارزمية'' هي مجموعة مُحددة من الخطوات التي نتبعُها لحل مسألةٍ ما؛ مثل مسألة إيجاد المسار الأقصر [1]. وتعني خوارزمية ديسكترا الشهيرة بحل مسألة إيجاد المسار الأقصر، وسُميت بهذا الاسم نسبةً إلى مُخترعها عالم الحاسوب الهولندي إدسخر ديكسترا4.
ويُمكننا استخدام هذه الخوارزمية؛ لخلق شجرة امتداد للمسارات الأقصر (انظر الشكل 2)؛ للعثور على المسار الأقصر المُمتد من عقدة البداية إلى جميع العُقد الأخرى الموجودة في الشبكة. ويمكن تحقيق ذلك بحساب المسافة المُمتدة من عقدة البداية إلى جميع العُقد الأخرى على حدة. وفي هذه المُناقشة، نستخدم المسافة باعتبارها التكلفة، كما يُمكن استخدام خوارزمية ديكسترا لحساب أي نوع من التكلفة.
في الشكل 2، نوضح طريقة استخدام خوارزمية ديكسترا؛ لاستنتاج شجرة امتداد المسار الأقصر للحصول على شبكة مُترابطة. تابع الشكل 2 أثناء قراءة شرحنا هذا، وشاهد الفيديو 1؛ لتجد شرح هذا المثال بالرسوم المُتحركة.
فيما يلي الخطوات التي نتبِعُها:
1 .نُظلل عقدة ''البداية''. (انظر العقدة A في الشكل 2) بالنسبة لجميع العُقد المجاورة لعقدة البداية، نضع القيمة الأولية ''للمسافة''؛ لتكون هي المسافة المُمتدة من عقدة البداية إلى تلك العٌقد المجاورة، والقيمة الأولية للعقدة ''النهائية''؛ لتكون هي عقدة البداية. وفي المثال الموضح في الشكل 2، عند اكتمال هذه الخطوة، نضع قيم ''المسافة'' والعقدة ''النهائية'' الخاصة بالعقدتين ''B'' و''C''، في حين تظل مُدخلات ''المسافة'' والعقدة ''النهائية'' الخاصة بالعُقد ''D''، و''E''، و''F'' خالية.
2. نُماثل العقدة غير المُظللة مع أقل قيمة ''مسافة'' (باستثناء الخانات الخالية)، ونصنفها باعتبارها عُقدتنا ''الحالية''. على سبيل المثال، إذا بدأنا باعتبار العقدة A عقدة البداية، فستكون العقدة C هي العقدة الحالية؛ لأن ''المسافة'' المُمتدة من العقدة A إلى العقدة C أقل من ''المسافة'' المُمتدة من العقدة A إلى العقدة B. وإذا تواجدت أي صلة بينهما، فسنختار العقدة ذات قيمة ''المسافة'' الأقل.
3. نُنفذ الخطوات التالية لجميع العُقد المجاورة غير المُظللة للعقدة ''الحالية'':
a. نُضيف ''مسافة'' العُقدة ''الحالية'' لقيمة الحافة المُمتدة من العقدة ''الحالية'' إلى العقدة المجاورة.
b. إذا كانت ''المسافة'' المُمتدة من الخطوة 3a أقل من ''مسافة'' العُقدة المجاورة (أو إذا كانت ''مسافة'' العقدة المجاورة لا تزال خالية)، فسنُجدد ''مسافة'' العقدة المجاورة لتُصبح هي ''المسافة'' التي حسبناها في الخطوة 3a، ونُعين العقدة ''النهائية'' المجاورة؛ لتُصبح هي العقدة الحالية.
4. عندما نُطبق الخطوة 3 على جميع العقد المُجاورة للعقدة ''الحالية''، نُظلل العقدة ''الحالية''، ونشطُب وسم العقدة ''الحالية''.
5. إذا ظُلِلَت جميع العُقد، فسننتقل إلى الخطوة 6. عدا ذلك، نعود مرة أخرى إلى الخطوة 2.
6. نُسلط الضوء على الحافة المُمتدة بين كل عقدة وعقدتها ''النهائية''؛ لإظهار شجرة امتداد المسار الأقصر من عقدة البداية.
الاستخدامات
باستخدام خوارزمية ديكسترا يُمكننا تحديد المسار الأقصر المُمتد من عقدة البداية إلى أي عقدة أخرى في الشبكة. إذ يُمكنك تحديد طريق مُناسب من منزلك إلى أي مكان تريد الذهاب إليه، إذا نظرت إلى منزلك على أنه عقدة البداية، ونظرت إلى وجهتك بصفتها عقدة أخرى في الشبكة.
ولنفترض أنك تُريد زيارة أماكن عدة قبل العودة إلى المنزل. كيف تعثر على الطريق الأفضل للوصول إلى هذه الوجهات، مع تقليل النفقات؛ مثل البنزين، والفنادق، والوقت؟ وباختصار، كيف يُمكننا العثور على المسار الأقصر الذي يمُر بجميع العقد الموجودة في شبكة، ومن ثم العودة إلى عقدة البداية؟ تُعرف هذه المسألة باسم ''مسألة البائع المتجول''، وتُعدُ امتدادًا لمسألة إيجاد المسار الأقصر6.
يُعدُّ العثور على المسار الأقصر أمرًا مُهمًّا؛ لحل المسائل المُختلفة التي تظهر في العديد من أنواع الشبكات المختلفة. على سبيل المثال، يُمكن للمسارات الأقصر زيادة فاعلية تخطيط المدينة. إذ يُمكن للمُهندسين المدنيين تخطيط المدينة في صورة شبكة، وتحديد أفضل الأماكن لبناء طرق؛ للحد من الازدحام المروري، وأفضل الأماكن لتركيب أنابيب الري؛ لتوصيل المياه إلى السكان [2]. كما يسمح العثور على المسارات الأقصر بنقل البيانات من حاسوب إلى آخر بسرعاتٍ عاليةٍ؛ مما يسمح بانتقال كميات كبيرة من المعلومات في ثوانٍ معدودة [1, 2].
ويوجد أيضًا العديد من أمثلة المسارات الأقصر في شبكات الاتصال، والشبكات الاجتماعية. على سبيل المثال، لنفترض أن كل شخص في الشبكة الاجتماعية يُمثل عقدة، وأن كل حافة تمثل الصداقة. حينئذٍ، يُمكنك استنتاج طريقة التواصل مع شخصٍ خارج مجموعات صداقاتك؛ بواسطة الاتصالات التي يقوم بها أصدقاؤك. إذ إن المسارات الأقصر للاتصالات (كما هو الحال في الصداقات) بين شخصين عشوائيين في الولايات المتحدة الأمريكية، أقصر مما قد يعتقده المرء. وفي المتوسط، توجد أقل من ستِ خطوات بين الشخص الأول، والشخص النهائي في مثل هذا المسار [3]! ويوضح ذلك القِصَر المثالي للمسارات الأقصر الموجودة بين الأشخاص ''ظاهرة العالم الصغير''، كما ساعدت أطوال المسارات القصيرة هذه في وجود مصطلح ''ست درجات من التباعد'' [1].
فخلال جائحة كوفيد-19 الأخيرة، كان العثور على المسارات الأقصر مُفيدًا؛ لتقليل نسبة التعرُّض للفيروس كورونا. على سبيل المثال، عند الانتقال إلى مُجمع تُجاري على مدار العام ونصف العام الماضيين، استفاد الأشخاص من العثور على المسارات الأقصر؛ لشراء المواد الغذائية التي توجد في البقالة (بمراعاة تفادي مُلامسة أشخاص آخرين، بواسطة التباعُد الجسدي) [4, 5].
الخُلاصة
المسارات الأقصر مُهمة عند الانتقال من مكانٍ إلى آخر. إذ يُمكن استخدامها بطرق عديدة مع الأشكال المُختلفة من الشبكات، ويمكنها أن تُساعد في حل العديد من مشاكل العالم الحقيقي، من التخطيط لقضاء إجازة عائلية، إلى استكشاف كيفية ارتباط عالمنا، تعد دراسة أقصر المسارات على الشبكات مهمة للغاية، وتشكل الأساس لتحقيقات أكثر تعقيدًا.
مسرد للمصطلحات
الشبكة (Network): ↑ هي مجموعة من الأشياء (تُسمى العُقَد)، والروابط (تُسمى الحواف) القائمة بينها.
العُقدة (Node): ↑ هي الأشياء الموجودة في الشبكة، والتي تتصل بأشياء أخرى. على سبيل المثال، تُمثل الأماكن والطُرُق الموجودة في الشكل 1 المعنى الحقيقي للعقدة.
الحافة (Edge): ↑ هي عبارة عن أحد الأشياء التي تربط عقدتين ببعضهما. على سبيل المثال، الطريق من منزلك إلى المدرسة يمثل حافة.
المسار (Path): ↑ هو سلسلة من الحواف المُمتدة من عقدة البداية إلى عقدة الوجهة.
التكلفة (Cost): ↑ هي قياس كمية الجهد الذي يتطلبه التنقل على طول إحدى الحواف على الشبكة. وفي الواقع، قد تُستخدم التكلفة لقياس المسافة، أو الوقت، أو أي شيء آخر.
المسار الأقصر (Shortest Path): ↑ هو المسار المُمتد من إحدى عقدات البداية إلى عقدة الوِجهة، بأقل تكلفة إجمالية مقارنة بجميع المسارات المُمتدة من البداية حتى الوجهة.
شجرة امتداد المسار الأقصر (Shortest-Path Spanning Tree): ↑ عبارة عن جزء من شبكة مُتصلة، تبدأ من عقدة بداية مُحددة، وتُحدد المسار الأقصر المُمتد منها إلى العُقد الأخرى الموجودة في الشبكة. على سبيل المثال، إذا احتوت الشبكة على 6 عُقد، فسيُشير ذلك إلى وجود 5 من أقصر المسارات في شجرة امتداد المسار الأقصر. وتحتوي شجرة امتداد الشبكة على جميع عُقد الشبكة. بالإضافة إلى ذلك، نظرًا لأن شجرة الامتداد هي نوع من الشبكات يُعرف باسم ''الشجرة''؛ تمتلك أي عقدتين من العُقد الموجودة بها مسارًا واحدًا فقط بينهما.
إقرار تضارب المصالح
يعلن المؤلفون أن البحث قد أُجري في غياب أي علاقات تجارية أو مالية يمكن تفسيرها على أنها تضارب محتمل في المصالح.
إقرار
نُعرِبُ عن امتنانا للقُراء الصِغار نيا تشيو، وتارين تشيو، وزوي تشيو، وتيخوإلينغ، وحكيم هانسن على تعليقاتهم المُثمرة. ونشكُر أعضاء عائلاتهم - ليندي تشيو، وكريستينا تشاو، وتيم إلينغ، وستيرلينغ هانسن - لجعلنا على اتصال معهم، والتماس آرائهم. ونُعرب عن امتنانا لكلٍ من ليندي تشيو، وميشيل لي، وتوماس ريكسين، وأكراتي ساكسينا على تعليقاتهم المُثمرة. كما نشكُر مُراجعينا الصغار، ومُعلميهم؛ على اقتراحاتهم الرائعة. كما تقدَّر MAP الدعم المُقدم من المؤسسة الوطنية للعلوم (رقم المنح 1922952)، بواسطة برنامج Algorithms for Threat Detection (ATD).
المراجع
[1] ↑ Newman, M. E. J. 2018. Networks, 2nd Edn. Oxford, UK: Oxford University Press.
[2] ↑ Cramer, C., Porter, M. A., Sayama, H., Sheetz, L., and Uzzo, S. (eds). 2015. Network Literacy: Essential Concepts and Core Ideas. Available online at: http://tinyurl.com/networkliteracy
[3] ↑ Milgram, S. 1967. The small-world problem. Psychol Today 1:61–7. doi: 10.107/e400002009-005
[4] ↑ Brooks, H. Z., Kanjanasaratool, U., Kureh, Y. H., and Porter, M. A. 2021. Disease detectives: Using mathematics to forecast the spread of infectious diseases. Front. Young Minds 9:577741. doi: 10.3389/frym.2020.577741
[5] ↑ Ying, F., and O’Clery, N. 2021. Modelling COVID-19 transmission in supermarkets using an agent-based model. PLoS ONE 16:e0249821. doi: 10.1371/journal.pone.0249821
مُلحق
دليل الإجابة
النشاط 1: يُمثل (المسار الرئيسي، ومسار شجرة الدردار، ومسار الطالب) أحد المسارات المُمكنة. ويُمثل (المسار الرئيسي، ومسار شجرة البلوط، ومسار شجرة النخيل، ومسار الطالب) أحد المسارات الأخرى المُمكنة. ويُمثل (مسار شجرة الصنوبر، ومسار شجرة القيقب، ومسار الطالب) المسار الثالث المُمكن اتباعه.
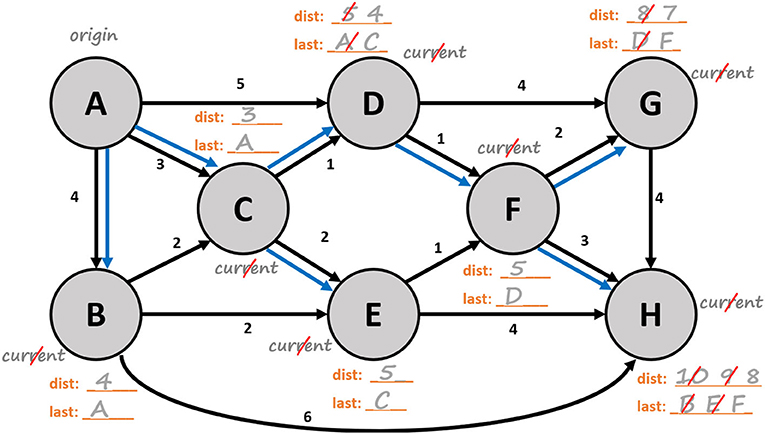
النشاط 2: يُعد هذا أحد أمثلة شجرة امتداد المسار الأقصر المُكتملة، للشبكة الموجودة في الشكل 3. تابع شرحنا في الفيديو 2.
- الفيديو 2 - مُراجعة الشكل 2: تابع شرح هذا الفيديو؛ للعثور على شجرة امتداد المسار الأقصر للشبكة الموجودة في الشكل 3.
- يُمكنك تنزيل نسخة قابلة للطباعة من الشكل 3 (تُسمى ''ورقة تدريبات النشاط 2'')، عبر الرابط https://drive.google.com/file/d/1rNONK-cmy4gq_aCJRnAYpe9Y2HSeq2A1/view.
الحواشي
[1] ↑ ويكيبيديا، الموسوعة الحرة. 2020. مسألة إيجاد المسار الأقصر. مُتاحة على الإنترنت عبر: https://en.wikipedia.org/wiki/Shortest_path_problem (اِطُلِعَ عليها بتاريخ 20 أغسطس 2020).
[2] ↑ عند نُطق كلمة DIJKSTRA بالإنجليزية، لا نلفظ حرف ''J''.
[3] ↑ موقع Code.org. 2020. دليل الأنشطة U2L07— خوارزمية ديكسترا لإيجاد المسار الأقصر. مُتاحة. على الإنترنت عبر: https://docs.google.com/document/d/15N7aHAoWG1_9VIcDHNZRygzFK0hle-EHlmHu0PZI8D4/view (اِطُلِعَ عليها بتاريخ 20 أغسطس 2020).
[4] ↑ ويكيبيديا، الموسوعة الحرة. 2020. Edsger W. Dijkstra. مُتاحة على الإنترنت عبر: https://en.wikipedia.org/wiki/Edsger_W._Dijkstra (اِطُلِعَ عليها بتاريخ 20 أغسطس 2020).
[5] ↑ يُمكنك تنزيل نسخة قابلة للطباعة من الشكل 3 عبر https://drive.google.com/file/d/1rNONK-cmy4gq_aCJRnAYpe9Y2HSeq2A1/view.
[6] ↑ طالع الرابط التالي https://www.youtube.com/watch?v=q8nQTNvCrjE&t=35s.
