ملخص
نقدم في هذا المقال عرضًا موجزًا لعلم الشبكات من خلال تسليط الضوء على أهمية نماذج الشبكات. سنناقش أصول الشبكات ونَصِف الدراسات المبكرة. ثم سنشرح الدور المهم الذي تلعبه الشبكات الجينية في علم الأحياء لفهم الطريقة التي تسبب بها الجينات بعض السمات الجسدية في الكائنات الحية. وإلى جانب علم الأحياء، يمكن العثور على الشبكات بشكل أساسي في جميع مجالات العلوم، بما في ذلك الكيمياء، والطب، والأعمال، والأموال والعلوم الاجتماعية. ينتج مجتمعنا الرقمي كميات كبيرة من البيانات ويمكن إنشاء الشبكات من هذه البيانات من خلال استخدام الأساليب الإحصائية. يمكن استخدام تلك الشبكات بعد ذلك لمساعدتنا على فهم العديد من مظاهر المجتمع ولتحسين حياتنا في نهاية المطاف.
ما الشبكات ومن أين تأتي؟
يحكي لنا برج بابل قصة الكتاب المقدس، حيث شتت الله ألسنة الناس الذين يحاولون بناء البرج للوصول إلى الجنة أو السماء، من خلال إدخال العديد من اللغات بينهم. بهذه الطريقة، لم يتمكن الناس من فهم بعضهم البعض مرة أخرى واضطروا إلى الاستسلام. بمعنى آخر، توفر الشبكات لغة رياضية تسمح للعلماء من مختلف المجالات بفهم بعضهم البعض. يجعل هذا الشبكات بمثابة أدوات مهمة تسمح لنا بالعمل على أصعب المشكلات التي يمكن تخيلها [1]. يُعرف مجال استخدام الشبكات لحل المشكلات المعقدة باسم علم الشبكات [2].
غالبًا ما يتم استخدام المصطلحين المخطط والشبكة بالتبادل. عادةً ما يشير المخطط إلى شكل رياضي لا يحتاج إلى تمثيله في العالم الحقيقي. فعلى الرغم من أن العلماء درسوا الشبكات لأكثر من 200 عام (بواسطة أشخاص مثل Euler وCayley)، فإن فكرة المخطط أحدث كثيرًا ويمكن تتبع جذورها إلى عالم الرياضيات König في فترة ثلاثينيات القرن الماضي، أي قبل أقل من 100 عام.
في أبسط أشكاله، يتم تعريف المخطط رياضيًا كالتالي:
التعريف1.1: الزوج G = (V, E) حيث v تمثل مجموعة منتهية من الرؤوس (نوع من النقاط الهندسية) وE مجموعة من الأضلاع حيث تعرف بالمخطط المنتهي غير الموجه.
يمكن فهم هذا التعريف بالطريقة التالية: يتكون المخطط من نوعين فقط، وهما العقد التي تسمى أيضًا الرؤوس (يمثلها الرمز V) والأضلاع وتسمى أيضًا الروابط (تمثلها E). تمثل V هنا مجموعة تحتوي على بعض العناصر، على سبيل المثال، V = {a, b, c, . . . }، وE هي مجموعة أخرى تحتوي على المعلومات حول الروابط بين العناصر في المجموعة V، على سبيل المثال، .E = {(a, b), (a, c), . . . } يشير المصطلح إلى مجموعة أخرى تحتوي على جميع الأزواج الممكنة من العقد التي يمكن تكوينها من العقد الموجودة في المجموعة V. وبالتالي، فإن المعنى يشبه العوامل الرياضية ثنائية التسمية إذا كانت V عددًا صحيحًا موجبًا. الرمز ⊇ في يعني أن جميع العناصر في المجموعة E مضمنة أيضًا في المجموعة وبالتالي، تكون E مجموعة فرعية من ويشمل ذلك الحالة التي تكون فيها جميع العناصر في موجودة أيضًا في E. في الشكل 1 (اليسار)، نعرض مثالًا ملموسًا للشبكة.
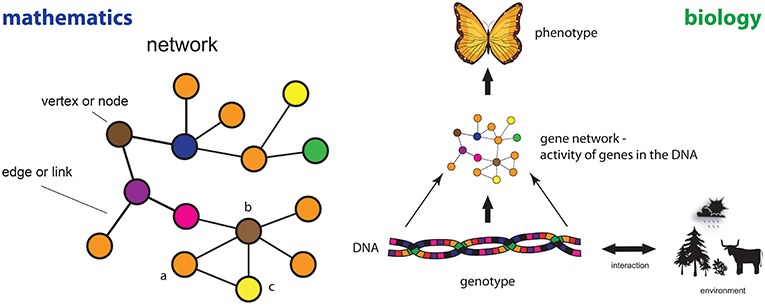
- شكل 1 - اليسار: مثال على إحدى الشبكات الرياضية والأجزاء التي تحددها.
- اليمين: شكل مبدأ الوراثة اللاجينية. يظهر إحدى الشبكات الجينية على هيئة اتصال بين النمط الجيني للكائن الحي (الحمض النووي الخاص به) والنمط الظاهري (الطريقة التي يظهر بها الكائن الحي).
قد يتساءل القارئ عن طريقة كتابة التعريف الرياضي للشبكة. وهذا ما يسمى المفهوم المجرد. فإذا أراد أحد الأشخاص دراسة الشبكات على مستوى متقدم، فإن هذه المعادلات مرتبطة بالمجال ويلزم الاهتمام الشديد بمبدأ التجرد بشكل عام في مجموعة مهارات الفرد.
من بين الشبكات الرياضية الأولى التي تمت دراستها الشبكات العشوائية. درس Erdös و Rényi هذه الشبكات في ستينيات القرن الماضي. حيث يتم الحصول على مخطط عشوائي يحتوي على عقد N من خلال ربط كل زوج من الرؤوس مع احتمالية ثابتة p. على الرغم من تركيبته البسيطة، فإن دراسة خصائصه الرياضية معقدة للغاية، وقد عمل أجيال من العلماء على حل هذه المشكلة.
أين نجد الشبكات؟
في علم الأحياء، تظهر أهمية الشبكات بسبب العمليات والأنظمة الحيوية التي تحتاج إلى الدراسة بشكل شامل (كل جزء على حدة) [3]. وهذا يعني أنه لا يمكن اختزال الأنظمة الحيوية إلى أجزاء صغيرة بشكل عشوائي، إلا أن الحجم الأدنى من هذا الجزء لا يزال بحاجة إلى أن يكون فعالًا بمعنى أن تنجح الكائنات الحية المعنية.
جاءت إحدى الأفكار الأولية في هذا الصدد من Conrad Waddington، الذي تصور فكرة مشهد الوراثة اللاجينية في فترة الأربعينيات [4]. الوراثة اللاجينية هنا تعني دراسة التغيرات التي تطرأ على النمط الظاهري الوراثي (انظر الشكل 1) والتي لا تغيّر الحمض النووي. تظهر فكرته الرئيسية في الشكل 1 (اليمين). على المستوى الجزيئي داخل إحدى الخلايا الحيوية بأحد الكائنات الحية (نبات أو حيوان أو إنسان)، يمكن تمثيل التفاعلات بين الجينات ونواتج الجينات (البروتينات) على هيئة شبكة جينية، على سبيل المثال، على هيئة شبكة نسخ تنظيمية أو شبكة بروتينات. تتوافق العقد في هذه الشبكة مع الجينات وتتوافق الحواف مع التفاعلات بين الجينات. يعني هذا أن الشبكات تظهر بشكل طبيعي في دراسة التفاعلات الجزيئية مثل تصورها التخطيطي وتمثيلها الرياضي [5]. استنادًا إلى محتوى الحمض النووي للكائن الحي وتفاعله مع البيئة (النظام الغذائي، ونمط الحياة، وغير ذلك)، يتغير هيكل الشبكة الجينية بسبب تغير أنماط نشاط الجينات وكنتيجة لذلك يظهر النمط الظاهري (المظهر المادي، مثل لون أجنحة الفراشة وشكلها) للكائن الحي.
إمكانية استخدام الشبكات في العديد من المجالات المختلفة
تعد الشبكات أدوات شديدة المرونة ويمكن استخدامها في العديد من المجالات بالإضافة إلى علم الأحياء. ترجع هذه المرونة إلى ثلاث خصائص رئيسية للشبكات. أولًا، يمكن للشبكات أن تجعل التفاعلات المعقدة بين جميع أجزاء النظام المختلفة مرئية. ثانيًا، تكوّن الشبكات تمثيلًا رياضيًا للنظام يمكن دراسته ومعالجته. ثالثًا، تمثل الشبكة هيكل البيانات التي يمكن حفظها بشكل ملائم على جهاز كمبيوتر وتحليلها بعدة طرق مختلفة، على سبيل المثال، استخدام الأساليب الإحصائية للعثور على مجتمعات العقد المتصلة اتصالًا وثيقًا.
ونظرًا لهذه المرونة، تُستخدم الشبكات في العديد من المجالات المختلفة، وتشمل الكيمياء، والفيزياء، والأحياء، والطب، والأعمال، والأموال ووسائل التواصل الاجتماعي. إليك قائمة بأهم الشبكات من بين هذه المجالات وفيمَ يمكن استخدامها للدراسة.
- البُنى الكيميائية، لدراسة الطريقة التي ترتبط بها المركبات الكيميائية ببعضها ببعض.
- شبكات التمثيل الغذائي، لدراسة كيفية قيام الكائنات الحية بأشياء مثل هضم الطعام، والنمو والتطور.
- شبكات تبادل الإشارات، لدراسة الاتصالات الجزيئية بين البروتينات.
- شبكات نسخ تنظيمية، لدراسة تنشيط الجينات.
- شبكات تفاعل البروتينات، لدراسة تكون المركبات المعقدة.
- الشبكات المالية لدراسة المحافظ الاستثمارية المثلى.
- تراكيب المستندات القائمة على المخططات، لدراسة أساليب الكتابة.
- شبكات خاصة بسلوكيات المستهلكين، لدراسة عادات التسوق عبر الإنترنت.
- شبكات اقتصادية، لدراسة الأنماط التجارية العالمية.
- شبكات اجتماعية، لدراسة العلاقات الإنسانية.
في الشكل 2، يمكنك رؤية مثالين عن الشبكات الحقيقية. هذه الشبكات من نوع خاص وتسمى شبكة ثنائية الأطراف. تتكون الشبكات ثنائية الأطراف من نوعين من العقد، مشار إليهما بلونين (الأزرق والبرتقالي). يستند معنى هذه العقد إلى المشكلات محل الدراسة. بخصوص الشبكة الاجتماعية المعروضة، تشير العقد الزرقاء إلى الممثلين والعقد البرتقالية إلى الأفلام التي مثّل فيها هؤلاء الممثلون. على سبيل المثال، يتم عرض حقيقة أن Harrison Ford قد لعب دورًا في فيلم Star Wars في الشكل 2. بخصوص الشبكة المالية المعروضة، تشير العقد الزرقاء إلى المستثمرين والعقد البرتقالية إلى الأسهم التي اشتراها المستثمرون. لقد عرضنا الشبكة الاجتماعية والشبكة المالية متراكبتين مع بعضهما بعضًا لأننا أردنا التأكيد مرة أخرى على السمات المجردة للشبكات. بالنسبة لهاتين الشبكتين، يمكنك التدرب على جعل الوضع محددًا من خلال التركيز على شبكة واحدة في كل مرة وتجاهل الأخرى تمامًا. يعلمك هذا التمرين كيفية التعامل مع هذا الوضع المجرد.

- شكل 2 - فيما يلي مثالين على تطبيقات الشبكات.
- يمثل الشكل شبكة اجتماعية وشبكة مالية. لجعل الشبكة على اليسار محددة، يتم التركيز أولا على الشبكة العلوية ثم على الشبكة السفلية فقط. يمنحنا ذلك شبكتين فرديتين. ويوضح ذلك المعنى المجرد للشبكة اليسرى.
ما الذي تعنيه الشبكات؟
يعتمد المعنى الملموس للشبكات واستخدامها على المشكلات التي تمثلها. على سبيل المثال، يمكننا استخدام شبكة اجتماعية لمشاهدة الممثلين المرتبطين بنفس الفيلم، ولمشاهدة أي من الممثلين ظهروا في الأفلام نفسها معًا. أما من الناحية العملية، فيمكن أن يتوافق هذا مع مجموعة من الممثلين وفقًا لأنواع الأفلام. بالنسبة إلى نموذج المخططات الخاص بالبروتينات، يمكن للشخص أن يدرس الوحدات أو الهياكل المجتمعية للرؤوس، والتي يمكن أن تتوافق عمليًا مع النطاقات التطورية المحفوظة للبروتينات. بالنسبة إلى شبكة الكمبيوتر، يمكن للشخص دراسة عدد الرؤوس التي يمكن إزالتها من الشبكة مع الحفاظ عليها متصلة، ويمكن أن تشير من الناحية العملية إلى قوة مثل هذه الشبكات فيما يتعلق بهجمات المخترقين. بالنسبة إلى شبكة النسخ التنظيمية، يمكن للشخص تحديد العقد التي تحتوي على أعلى عدد من التوصيلات بالعقد الأخرى، ويحدد ذلك عمليًا الجينات المحورية ويمكن أن يشير إلى مدى أهمية مثل هذه الجينات.
هذه بضع أمثلة فقط توضح كيف يمكن استخدام الشبكات المجردة لحل المشكلات الملموسة في العديد من مجالات الأبحاث.
كيف نحصل على الشبكات؟
على عكس الشبكات الموضحة في الشكل 2، والتي تعد بسيطة وسهلة الفهم إلى حد ما، يوجد المزيد من الشبكات المجردة.
تحتاج هذه الشبكات إلى الاستدلال عليها من البيانات من خلال استخدام أساليب من الإحصائيات وتعلّم الآلة. في الشكل 3، نستعرض مظاهر مجتمعنا الرقمي الذي يسمح لنا بإنتاج كميات هائلة من البيانات حول كافة مظاهر الحياة تقريبًا، بما في ذلك الصحة (الفحوص الطبية، والهواتف الذكية، والساعات الذكية وغير ذلك)، والأعمال (سوق البورصة، وموقع أمازون وغير ذلك) ووسائل التواصل الاجتماعي (Twitter، وFacebook وغير ذلك). يمكن تحليل البيانات الواردة من هذه المجالات بمساعدة أجهزة الكمبيوتر لإنتاج نماذج الشبكات. يمكن أن توفر لنا نماذج الشبكات هذه رؤى جديدة حول العديد من مظاهر مجتمعنا، مثل الاقتصاد، أو أساليب رعاية المرضى، أو سلوك المستهلكين، والتي يمكن استخدامها بعد ذلك لمساعدتنا على تحسين حياتنا.
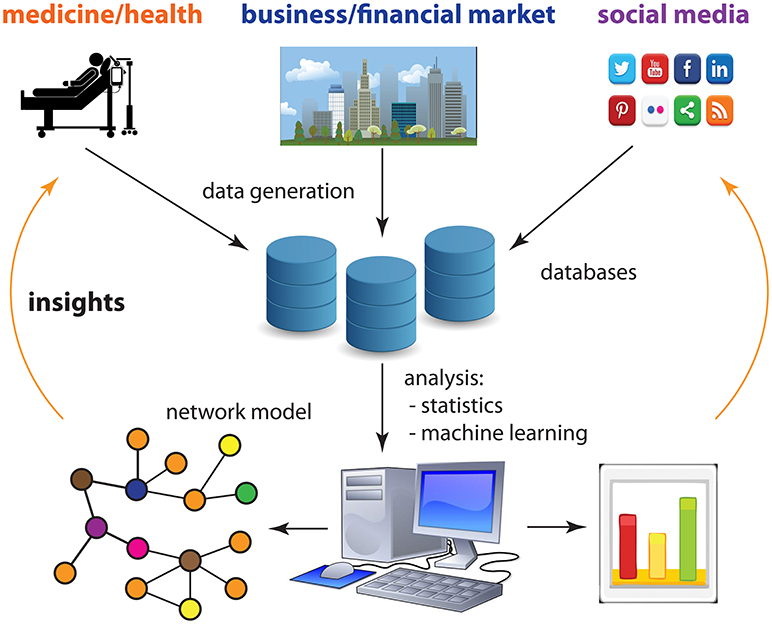
- شكل 3 - يسمح لنا مجتمعنا الرقمي بإنتاج كميات هائلة من البيانات حول كافة مظاهر الحياة تقريبًا، بما في ذلك الصحة، والأعمال ووسائل التواصل الاجتماعي.
- يمكن تحليل هذه البيانات بواسطة أجهزة الكمبيوتر لإنشاء نماذج شبكات تعلمنا أشياء جديدة حول مجتمعنا وتسمح لنا بإدخال تحسينات على تلك المجالات المجتمعية.
الخلاصة
نتمنى أن يكون عرضنا الموجز قد أظهر أن الشبكات توفر لغة أساسية تسمح لنا بمعالجة المشكلات الأكثر إثارة للاهتمام وأهمية في المجتمع والعلوم. ومع ذلك، يلزم أن نتسلح بفهم قوي للرياضيات حتى تتمكن من دراسة نماذج الشبكات هذه.
مساهمة المؤلف
قام FE-S بتصور الدراسة. أسهم جميع المؤلفين في كافة مظاهر إعداد الورقة البحثية هذه وكتابتها. اعتمد جميع المؤلفين النسخة النهائية.
مسرد للمصطلحات
التعريف الرياضي (Mathematical definition): ↑ هو وصف يتم التعبير عنه بلغة الرياضيات ويكون مهمًا للغاية.
الوراثة اللاجينية (Epigenetic): ↑ هي دراسة التغيرات التي تطرأ على النمط الظاهري الوراثي والتي لا تنطوي على تغييرات في الحمض النووي. ويعني ذلك المكونات الموجودة أعلى الجينات (السابقة اليونانية "epi" تعني "أعلى").
الحمض النووي (Dna): ↑ حمض الديوكسي ريبونيوكليك، هو مادة ذاتية النسخ تتواجد في جميع الكائنات الحية تقريبًا كمكون رئيسي للكروموسومات وحامل للمعلومات الوراثية.
إقرار تضارب المصالح
يعلن المؤلفون أن البحث قد أُجري في غياب أي علاقات تجارية أو مالية يمكن تفسيرها على أنها تضارب محتمل في المصالح.
المراجع
[1] ↑ Emmert-Streib, F., Dehmer, M., and Shi, Y. 2016. Fifty years of graph matching, network alignment and network comparison. Inform. Sci. 346–347:180–97. doi: 10.1016/j.ins.2016.01.074
[2] ↑ Barabási, A.-L. 2013. Network science. Philos. Trans. R. Soc. A 371:20120375. doi: 10.1098/rsta.2012.0375
[3] ↑ Emmert-Streib, F. and Dehmer, M. 2011. Networks for systems biology: conceptual connection of data and function. IET Syst. Biol. 5:185. doi: 10.1049/iet-syb.2010.0025
[4] ↑ Waddington, C. H. 1957. The Strategy of the Genes. London:: George Allen & Unwin.
[5] ↑ Emmert-Streib, F. and Glazko, G. V. 2011. Network biology: a direct approach to study biological function. Wiley Interdiscipl. Rev. Syst. Biol. Med. 3:379–91. doi: 10.1002/wsbm.134
