Abstract
This article is based on an interview between the two authors.
Small particles, such as single photons, electrons, atoms or charged atoms (called ions), can experience a very different world from that which we usually perceive. While in our daily life, things seem to be reasonably predictable, continuous, and well-defined, in the “quantum” world of single or small numbers of particles, there are surprises and many unexpected “non-classical” behaviors. In addition to its complexity, the world of small particles opens up some very interesting possibilities for applications to practical problems. To take advantage of the amazing properties of small particles, scientists and other researchers have developed various techniques for holding and isolating photons, electrons, atoms, and ions and manipulating their behavior. In this article, we will try to give you a glance into the fascinating lives of small particles, tell you about techniques for working with them, and mention exciting new potential applications that take advantage of their unique behaviors.
Prof. David Wineland shared the 2012 Nobel Prize in Physics with Prof. Serge Haroche, Collège de France, Paris “for ground-breaking experimental methods that enable measuring and manipulation of individual quantum systems”.
The Lives of Small Particles
The world of atoms and subatomic particles is extremely rich and fascinating. In it, we encounter many peculiar phenomena and find that our daily intuition about how things work does not apply in the atomic and subatomic world. One interesting feature of this world, which is often called the quantum world, is its apparent discreteness. Unlike our daily world, the world of particles appears to not be continuous, as if there are sudden jumps between different conditions. For example, we know that electrons in atoms can occupy only specific regions around the nucleus, called atomic orbitals. (In quantum mechanics, we learn that the electrons do not act like point particles orbiting the nucleus (like planets orbiting the sun); rather, they are described by “wavefunctions” where, in effect, their position is spread out in space.). In each of these atomic orbitals, electrons have a certain amount of energy, called their energy level. When an atom releases energy by emitting a light particle called a photon, the energy of an electron inside the atom appears to instantaneously jump from one energy level to another, lower energy level. Similarly, when an atom gains energy by absorbing a photon, an electron appears to suddenly jump from an initial orbital to a final orbital with a higher energy level. In fact, the “jumps” are not instantaneous but in some cases, they take only a very short time, on the order of 1 billionth of a second.
The theory in physics that best explains the wonderous world of atoms and subatomic particles is called quantum mechanics. Although the foundations of quantum mechanics were laid almost a century ago, there are still some puzzles that we do not yet fully understand about the fundamental behavior of particles, which are the building blocks of the material world. However, many techniques have been developed that help us to better understand and control the behavior of particles. Next, we will briefly tell you about two such techniques—one for trapping particles (even a single particle) in a specific location, and the other for slowing down their motion, or cooling them.
Trapping Many Particles
Particles typically move around a lot. When we work with particles, we often want them to be confined in a specific location. We often study electrons and atomic ions, which are affected by electric fields. By arranging electrodes in a specific geometry, and applying voltage to them, we can produce electric fields that trap our electrons or ions in a specific location [1, 2]. An analogy is to think about marbles in a bowl: our particles are the marbles and the electric fields effectively provide the bowl (Figure 1A). The center of the bowl is like the center of the electric field “trap”: if the particles move in any direction away from the bottom of the trap (or bowl) they will experience a “push” back toward the center. Much like gravity keeps marbles in the bottom of the bowl, the electric field keeps the particles confined—near the center of the trap. Professors Wolfgang Paul and Hans Dehmelt shared half of the 1989 Nobel Prize in physics for their development of traps for ions and electrons [1, 2].
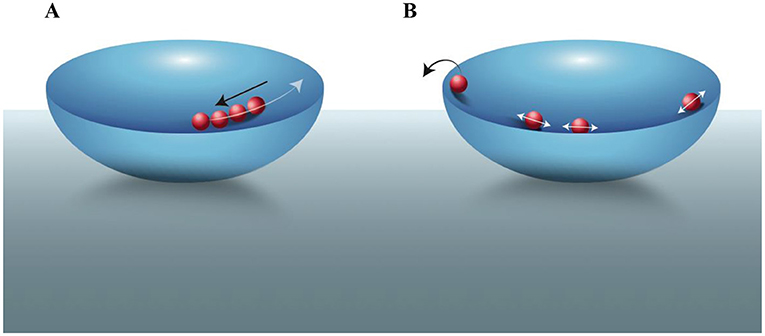
- Figure 1 - Trapping particles–the bowl-and-marbles analogy.
- Electrons and ions moving in an electric field “trap” can be viewed as marbles in a bowl. (A) When particles move away from the center of the electric field bowl (white arrow), they are pushed back toward the center (black arrow), keeping them trapped inside the bowl. (B) If we want to trap only a single particle, we can for example, first trap multiple particles and, by applying oscillating electric fields and increasing the movement of particles, we can eliminate particles one-by-one, by “evaporating” them out of the bowl (black arrow), until only a single particle is left [3].
Trapping a Single Particle
Sometimes we need to control particles very precisely. Working with groups, or “ensembles,” of particles is sometimes more convenient, both because it is easier to trap many particles at once and because it is easier to measure the larger signals (the electric currents induced in the electrodes by the movement of the charges) generated by many particles together compared to the small signals of a single particle. But when working with many particles, it is harder to control them as precisely as we can control one particle. Think of this like trying to keep an eye on one kid in a class compared to keeping an eye on many kids at once—you can imagine how much harder the second case is.
We can control the speed of one particle with high precision, including bringing the particle to nearly a complete stop, but it is more difficult to control the speeds of many individual particles in a group with the same precision (When particles in a group collide, it can perturb their internal energy levels in an uncontrolled way.). Therefore, if we need very high control and precision (as we need for atomic clocks, as you will see below), we sometimes need to work with single particles to finely control the particle’s motion and minimize errors that occur when working with many particles [3].
To trap a single charged particle, we can first trap several particles as in Figure 1A. Then, we apply an oscillating electric field to the particles, so that occasionally a particle will “fly out” of the trap. In our bowl-and-marbles analogy, you can think about this as increasing the motion of the marbles inside the bowl, until a marble “jumps over” the edge of the bowl (Figure 1B). Each time a particle jumps out of the bowl, we can measure a sudden, discrete reduction in the total oscillating electrical current induced in the electrodes (as in [3]). We repeat this process until the current of the system is equal to the current of a single particle so that we know we are left with only one trapped particle [1]. Then, we can either study its properties, and/or use its known properties for specific applications [1, 2]. When working with certain atomic ions we can scatter laser light from them; the total observed scattering is proportional to the number of ions, which enables us to tell when we have a single ion in the trap.
Cooling Atoms With Laser Beams
Another important technique for controlling particles is slowing or cooling them to very low temperatures using lasers, so that they are barely moving. This is called laser cooling. As you have learned, electrons move around the nucleus only in specific energy levels. When a photon approaches an atom, it is absorbed by the atom only if it has exactly the right amount of energy to transfer electrons from one energy level to another; otherwise, the light just passes through the atom. As you might know, the energy that photons carry is directly related to another property of light called frequency (the number of cycles that a wave completes in 1 s), such that photons with higher energy have higher frequencies, and vice versa (to learn more about frequency and energy, see here).
When an atom moves against the direction of light such as that in a laser beam, the frequency of the light experienced by the atom has higher frequency and therefore is “more energetic,” compared to the case when the atom moves away from the light source (Figure 2). This is called the Doppler effect. Therefore, if we tune the laser frequency slightly below the frequency (or energy) required for the transition between two electron orbits when the atom is at rest, then when the atom moves toward the laser, it will experience it as having a higher frequency and will absorb the light (red atom in Figure 2). Absorbing the light will slow down the atom due to the photon momentum imparted to the atom which reduces the atom’s momentum thereby reducing its speed. Think of it like two rugby players running toward each other, slowing down after they bump into each other. On the other hand, if the atom moves away from the laser (green atom in Figure 2), the laser beam frequency experienced by the atom will be shifted low and the probability that the laser beam photon will be absorbed by the atom will be reduced. Consequently, the atom will keep moving at approximately the same speed (to learn more about laser cooling, see this video). This differential effect between the atom moving toward vs. away from the laser means that we have a way to slow down the motion of an atom moving in a specific direction (toward the laser). Combining several lasers projecting from different directions, we can slow the atoms that are moving in all directions.
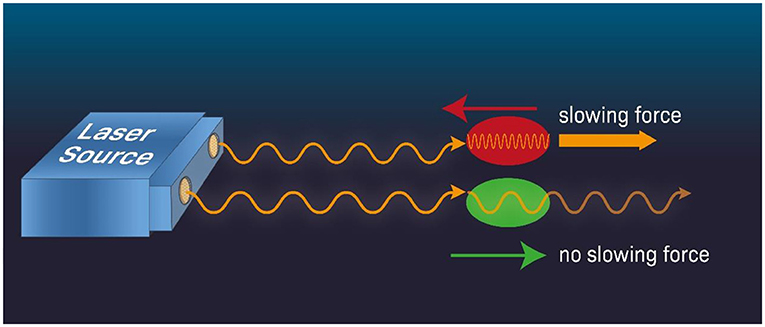
- Figure 2 - Laser cooling.
- When an atom moves against a laser beam (red) it experiences higher beam frequency (that is, photons of a higher frequency). If we tune the laser’s frequency slightly below the specific frequency that the atom absorbs when it is at rest, then the atom moving against the beam direction will experience, through the Doppler effect, photons of a higher frequency and absorb the laser’s light and slow down (think of the laser photon as if it is a hard object moving toward the atom and when they collide, the atom slows down). In contrast, an atom moving in the same direction as the laser beam (green) will only weakly absorb the laser photons, as the photon frequency is lower than the frequency for maximum absorption by the atom. Therefore, the atom will continue moving without its speed changing appreciably. Combining a few laser beams that project from different directions, atoms can be slowed down to very low speeds in all directions.
Atomic Clocks: Telling Time Accurately
Clocks are such a common part of our daily lives that we rarely stop to think about fundamental questions, such as how time is measured and what limits the accuracy of telling time. For scientists and engineers at laboratories like the Time and Frequency Division of the US National Institute of Standards and Technology (NIST), this is what they think about all day long! Their mission is to keep improving the accuracy of clocks, and to measure time more and more precisely. As for most experimental physicists, these scientists act like detectives, carefully identifying all the important factors and environmental effects that limit the accuracy of telling time. They then try to reduce these effects as much as possible to continually improve the accuracy of measuring time. These clock scientists have been working on this task since the 1950s when the first atomic clocks were demonstrated (to learn more about the history and operation of atomic clocks, see this article).
In general, to measure time intervals, we actually count the number of cycles of a reference frequency source, such as the oscillations of a mechanical pendulum or a piezoelectric quartz crystal oscillator (a device found in cell phones whose mechanical oscillations are driven by the electrical voltage applied on it.). If we know the frequency of our frequency source, we know how much time has passed by counting how many cycles were completed in a certain time interval (i.e., duration between two points in time). For example, if we know that the frequency of our source is 100 Hz (cycles per second), then we know that the duration of each cycle is 1/100 (or 0.01) second. The higher the frequency of the source, the more precisely we can define time intervals.
We can measure time internals very accurately using atomic clocks as our frequency source. This means that instead of using the low frequency of a mechanical pendulum, or the frequency of quartz crystal oscillator, we can use the very high frequency that corresponds to the frequency of photons that cause transitions between discrete energy levels of atoms. For example, we could shine a laser beam on atoms that have first been placed in their lowest energy electronic state and we observe the amount of absorption of the laser beam. When the absorption is maximized, we know that the laser beam frequency matches the frequency of photons that correspond to the energy difference between the two atomic energy levels. If the laser beam is not maximally absorbed, we change its frequency a little bit until the absorption is maximized, and satisfy this condition. Then, by counting the number of cycles of the laser oscillation we can precisely determine time intervals (Figure 3).
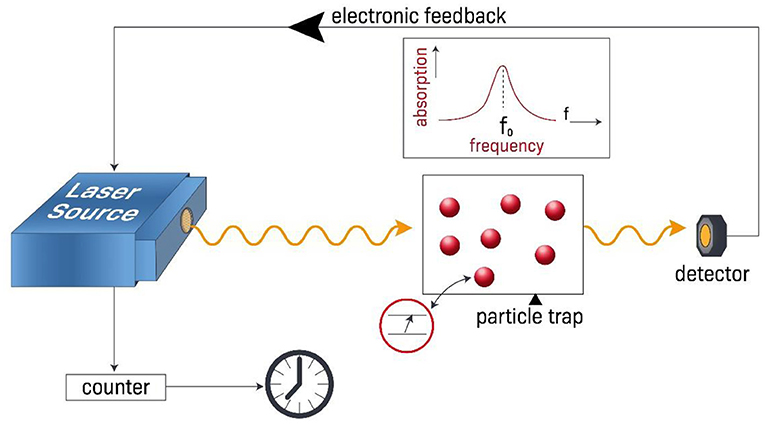
- Figure 3 - Principles of atomic clocks.
- When a laser beam is maximally absorbed by trapped and cooled atoms (red balls), it means that the laser’s frequency equals the frequency of photons required for electrons to “jump” from a lower energy level to a higher energy level (schematic in red circle). We tune the laser frequency using an electronic feedback system until the laser beam is maximally absorbed by the atoms. We then use a device count how many cycles the laser beam makes, which we then use together with the atom’s transition frequency to calculate how much time has passed. Because the laser has a very high frequency, the time for each oscillation cycle is very short and we can measure time intervals with very high precision.
Atomic clocks are used in satellites to detect your location using the GPS in your smartphone, for example. Knowing the speed of light and using synchronized atomic clocks to measure the time it takes for light to travel from the satellite to your smartphone enables the software to accurately compute your distance from the satellite. Using a network of time-synchronized satellites, your three-dimensional location can be determined. The atomic clocks in satellites must be very accurate, since very small errors in their time measurement, even on the scale of one millionth of a second, result in large errors of hundreds of meters in determining your location using GPS.
For many years, the best atomic clocks were based on a particular transition in a specific element (the “hyperfine” microwave transition in neutral atomic cesium which has a frequency of about 9.2 GHz, or about 9.2 x 109 Hz.). But for the last few years the most precise frequency standards are based on transitions that have frequencies near those of light waves corresponding to the colors of light we see with our eyes) around 1015 cycles per second [4] (To learn more about optical atomic clocks, see this article). Uncertainties in these frequencies due to environmental perturbations are at around 1 part in 1018 which implies that clocks based on these transitions would be uncertain to less than a second over the age of the universe (~13.7 billion years).
An important potential application that can utilize advanced techniques of laser cooling is called quantum computation. Quantum computation uses the quantum characteristics of atoms and ions or more macroscopic devices to perform certain complex computations much more efficiently than classic digital computers. For a brief introduction, see the Appendix.
Recommendations For Young Minds
We feel that the work we do is more like a hobby because we would probably be interested in the same things even if they were not part of our profession. That is something that we wish for you, too. We believe that you should find something that you really like, and if you like it, you will be willing to work hard and spend a lot of time on it, and then you are likely to be successful. Even if you change your mind about what you like, or what is interesting for you, that is fine. You obviously do not want to spend your time on something too far off from what you like to do anyway. Of course we also, think it is important to keep your eyes open and course-correct your decisions when needed.
For those of you who chose a career in science, it is also important to know that patience and perseverance will be required. In science, and specifically in scientific research, the fruits of your efforts are often not immediate. It takes time to develop the knowledge and skills required to perform high-quality research and gain new insights about the world. You must be able to endure some difficulty and persevere even when things do not go your way. If you do, you will eventually enjoy the fruits of your efforts and enjoy the wonder of discovery.
We want to also emphasize that, in our opinion, choosing a career or a path based on making money is a mistake. You are not likely to be very satisfied or successful if you focus only on supporting yourself financially. On a similar note, if you chase after prizes and awards, that would most likely not be a successful path either. We advise you to choose something you like and invest the hard work needed to progress toward a meaningful goal, instead of focusing on salary of social recognition.
Finally, we have some advice for those of you who intend to go to college. When you go to graduate school, you will be assigned to work on a particular project. From our experience, it is always useful not only to just focus on the exact topic that you are working on, but also to branch out a little bit and read some broader, related materials. This is exactly how David got the idea for laser cooling—by reading additional papers on topics not directly related to his project at that time. This eventually became a major milestone in his scientific career.
Appendix: Future Advances and Applications
The performance of atomic clocks will continue to improve. Frequency shifts due to many environmental perturbations on the atoms such as stray local electric and magnetic fields must be accounted for with increased precision. Two additional effects that must be included in clock comparisons come from Einstein’s theory of relativity and are separate forms of what is called “time dilation”—the slowing of time in one reference frame relative to another.
First, Einstein taught us that in a reference frame that is moving relative to us, say the frame attached to a moving atom or ion, time runs slower compared to us, as stationary observers in a lab. This shift is proportional to the average energy of motion of the ions, so that one of the benefits of laser cooling is that we can reduce the shift by about a factor of a million compared to room-temperature ions or atoms.
The second kind of time-dilation that Einstein taught us is that time runs slower in the presence of gravitation [the so-called “gravitational potential red shift” [5–7]]. This is not a big effect in our normal daily experience as can be illustrated by the following example: Suppose you and a twin sibling were separated at birth. You live at sea level; your twin has lived 1.6 km above sea level (for example, in Boulder, Colorado). After 80 years, your twin will only be about 0.001 s older than you.
This is of course a negligible effect in terms of typical human activities, but it can be observed with accurate clocks and needs to be taken into account when comparing clocks at different locations as in navigation via GPS.
As a simple demonstration of the effect, two separate clocks based on the same atomic transition in an ion were compared at the National Institute of Standards and Technology in Boulder, Colorado [5]. Initially the two clocks were at the same height but separated laterally by a few meters. The frequency ratio of the two clocks was unity to about 1 part in 1018. One of the clocks was then raised by 33 cm and the ratio of the frequencies of the two clocks was measured again. The frequency of the raised lock increased by about 4 parts in 1017, close to the expected result.
Even more dramatic demonstrations of the gravitational potential red shift were recently demonstrated by two groups using neutral atoms where the gravitational red shift was observed at millimeter scale [6, 7].
In addition to improved clocks, another important potential application based on controlling and manipulating individual quantum systems, is quantum information processing, which includes quantum computation (computer calculations performed using quantum elements) and quantum simulation (computer simulations that use quantum effects to understand physical phenomena). Although this topic is beyond the scope of this paper, we can give you an idea of this important field and where it is heading.
To do so, we first need to explain another peculiar phenomenon in the world of quantum particles, called superposition. Superposition refers to the fact that particles can represent two different energy levels at the same time. Consider the example of a single trapped ion being like a marble in a bowl. We can excite the ion’s motion with an oscillating electric field and create a classical-like condition where the marble rolls back and forth say between the left side and right side of the bowl. However, with our quantum tools we can also make a situation where at certain times the marble is simultaneously on the left and right side of the bowl in a ”superposition“ state. This is very counterintuitive and makes no sense in our everyday classical world, but it is the world quantum scientists live in.
Extending this idea to the energy levels of a single atom, we can make a superposition state where the atom is simultaneously in its lower and higher energy state. In practice, this is relatively easy to do. Previously, we spoke about a single atomic ion absorbing a single photon and making a transition from its lower to higher energy level. It turns out that if our laser beam is composed of many photons that are spread out in space in all directions perpendicular to the direction of the laser beam and we apply the laser for a particular duration, we can realize a situation where the atom is excited only ”half-way.“ That is, after the laser beam is switched off, the atom is in a superposition of its lower electron energy level and its higher energy level. So, superposition means a particle can simultaneously exist in multiple states (two in the above example) at any given moment.
The field of quantum computation is based in part on superposition of two states of a quantum system, atomic ions in the above example. As you might know, a normal computer is composed of basic units called ”bits,“ that can be in one of two states, which we call ”0“ and ”1.“ This two-state system, when combined with other similar two-state systems, can perform all the calculations of a conventional computer. The idea of quantum computation is that every basic unit, called a ”qubit“ (short for quantum bit) can be in a superposition of states, or multiple states at once.
To represent the state of a qubit as a superposition of the quantum states ”0“ and ”1“, we often use the notations “|0〉” and “|1〉.” We write the general superposition state of a qubit as α|0〉 + β|1〉, where |α|2 is the probability of the qubit being measured in state “0” and |β|2 is the probability of the qubit being measured in state “1.” When these probabilities are equal, what we call an equal superposition of states, one possible superposition state of the qubit can be |0〉 + ||1〉 (where |α|2 = |β|2 ).
Now, let’s see what happens in a larger system. If we look at a classical system with two bits, each being in one of the states “0” or “1”, we can represent a total of 22 = 4 numbers, which are: 00, 10, 01, or 11. The general state of an equivalent 2-qubit system would be α|00〉 + β|01〉 + γ |10〉 + δ|11〉, where the probability of measuring the states |00〉, |01〉, |10〉 and |11〉 are |α|2, |β|2,| γ| 2, and |δ|2, respectively. One example of a superposition of the four states the state would be the state |00〉 + |01〉 + |10〉 + |11〉 with a measurement probability of for each state). As you can see, a superposition of a 2-qubit system contains, or stores four (22) two-bit numbers simultaneously. In contrast, a classical two-bit system can only store one two-bit number (one of either 00, 10, 01, or 11).
Scaling this to even larger systems, we can see that a classical n-bit system can store one n-bit binary number comprised of “0”s and “1”s. However, a superposition of n qubits can store 2n n-bit numbers at once (that is 2n times more numbers compared to a classical system of the same size). This then indicates that when we perform an operation on one of the qubits in our n-qubit superposition, we operate on all 2n n-qubit states simultaneously. This suggests that a quantum computer can store and process a much greater amount of information than a classical computer with the same size, and is an example of “exponential scaling.” A dramatic example is that if we have 300 qubits we can store 2300 300-bit numbers simultaneously. A classical memory of this size would require more particles than exist in the universe! It is relatively easy to make such a state with trapped ions, but to make useful logic gates for a system this size is much harder [Implementation of quantum logic gates is beyond the scope of this paper, but some of the basic ideas can be found in [8]].
Therefore, for certain problems, in principle, quantum computers could be much more efficient and faster than classical computers and could solve problems that current conventional computers are incapable of solving. Beyond efficient number factoring (as proposed by Peter Shor), one anticipated application of quantum computers, then, is the ability to simulate the dynamics or behaviors of complex quantum systems, such as the action of molecules in a chemical that might be used in drug therapy, and study them using computer simulations without having to synthesize them in the lab. Similar simulations could also potentially teach us new things about physics, or they could solve difficult physics problems that classical computers cannot.
Many people are wondering when we will have the first quantum computer. The answer is that we already have quantum computers; but so far, the problems they solve can be solved by classical computers (maybe not as efficiently) or they solve problems that are not of practical interest. Building and improving quantum computers will likely be a gradual process—the first quantum computers will only be able to solve simple useful problems and, but as the field progresses, they will be able to do more complicated things. Perhaps in the next 10 years, we will be able to do something useful with quantum computers, like discovering something we did not know before, or simulating an interesting system for practical applications. That is something exciting for us to look forward to.
Additional Materials
The transcript of the interview between Prof. David Wineland and Noa Segev can be found here.
Glossary
Energy Level: ↑ Specific discrete energy value that a quantum system can have such as those of electrons in an atom.
Quantum Mechanics: ↑ A theory in physics describing the behavior and properties of atoms and other particles as well as more macroscopic systems like the vibrations of miniature mechanical oscillators.
Electrons: ↑ Fundamental particles in atoms which have a negative charge.
Electrodes: ↑ Typically metal structures that conduct electricity and can be used to create electric fields.
Laser Cooling: ↑ A technique that uses laser beams for slowing down and cooling atoms and ions.
Photons: ↑ Particles of light carrying a specific, discrete amount of energy proportional to their frequency. This was Max Planck’s idea and was followed subsequently by Einstein.
Momentum: ↑ A physical quantity defined as the product of the mass of a particle and its velocity. The higher a particle’s momentum is, the stronger the force it can impart on other particles.
Acknowledgments
We wish to thank Sharon Amlani for the illustrations in this article.
Conflict of Interest
The author NS declared that they were an employee of Frontiers, at the time of submission. This had no impact on the peer review process and the final decision.
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
[1] ↑ Paul, W. 1990. Electromagnetic traps for charged and neutral particles. Rev. Modern Phys. 62:531. doi: 10.1103/RevModPhys.62.531
[2] ↑ Dehmelt, H. 1990. Experiments with an isolated subatomic particle at rest. Rev. Modern Phys. 62:525. doi: 10.1103/RevModPhys.62.525
[3] ↑ Wineland, D., Ekstrom, P., and Dehmelt, H. 1973. Monoelectron oscillator. Phys. Rev. Lett. 31:1279. doi: 10.1103/PhysRevLett.31.1279
[4] ↑ Diddams, S. A., Bergquist, J. C., Jefferts, S. R., and Oates, C. W. 2004. Standards of time and frequency at the outset of the 21st century. Science. 306:1318–24. doi: 10.1126/science.1102330
[5] ↑ Chou, C. W., Hume, D. B., Rosenband, T., and Wineland, D. J. 2010. Optical clocks and relativity. Science. 329:1630–3. doi: 10.1126/science.1192720
[6] ↑ Bothwell, T., Kennedy, C. J., Aeppli, A., Kedar, D., Robinson, J. M., Oelker, E., et al. 2022. Resolving the gravitational redshift across a millimetre-scale atomic sample. Nature. 602:420–4. doi: 10.1038/s41586-021-04349-7
[7] ↑ Zheng, X., Dolde, J., Lochab, V., Merriman, B. N., Li, H., and Kolkowitz, S. 2022. Differential clock comparisons with a multiplexed optical lattice clock. Nature. 602:425–30. doi: 10.1038/s41586-021-04344-y
[8] ↑ Monroe, C. R., and Wineland, D. J. 2008. Quantum computing with ions. Sci. Am. 299:64–71. Available online at: https://www.scientificamerican.com/article/quantum-computing-with-ions/
