תַקצִיר
מאמר זה מבוסס על ראיון בין שני הכותבים. חלקיקים קטנים, כמו פוֹטוֹנִים בודדים, אלקטרונים, אטומים ואטומים שנושאים מטען חשמלי (הנקראים יוֹנִים), חווים עולם שונה מאוד מהעולם כפי שהוא נגלה לנו בדרך כלל. בעוד שחיי היום-יום שלנו צפויים למדי, המשכיים ומוגדרים היטב, ב'עולם הקְוָונְטִי' – עולמם של חלקיקים בודדים או ספורים – יש הפתעות והתנהגויות בלתי צפויות ו'לא רגילות' רבות. בנוסף למורכבותו, עולם החלקיקים הקטנים מציע אפשרויות מעניינות מאוד שאפשר ליישם על בעיות מעשיות. כדי לנצל את התכונות המדהימות של החלקיקים הקטנים, מדענים וחוקרים שונים פיתחו טכניקות מגוונות שנועדו לבודד ו'ללכוד' פוטונים, אלקטרונים, אטומים ויונים, ולהשפיע על התנהגותם. במאמר הזה ננסה לספק לכם הצצה אל חייהם המרתקים של החלקיקים הקטנים, נספר לכם על טכניקות העבודה איתם, ונציין איך אפשר לרתום את התנהגויותיהם הייחודיות לשימושים חדשים ומלהיבים בעתיד.
פרופסור דיוויד וָיְנְלֶנְד זכה בפרס נובל לפיזיקה לשנת 2012, במשותף עם פרופסור סֶרְז' הָרוֹש, מהקולז' דה-פראנס, פריז, ''עבור שיטות ניסוי פורצות דרך המאפשרות מדידה של מערכות קוואנטיות בודדות והשפעה עליהן''.
חייהם של החלקיקים הקטנים
עולמם של האטומים והחלקיקים התת-אטומיים הוא עשיר ומרתק. בעולם הזה, אנחנו נתקלים בהרבה תופעות מוזרות ומגלים שאי אפשר להחיל את האינטואיציה היום-יומית שלנו לגבי הדרך שבה דברים עובדים על העולם האטומי והתת-אטומי. אחת התכונות המעניינות של העולם הזה, שבדרך כלל נקרא 'העולם הקְוָונְטִי', היא הדִיסְקְרֶטִיוֹת (חוסר הרצף) המובחנת שלו. בניגוד לעולם היום-יומי שלנו, נראה שעולם החלקיקים אינו רציף – כאילו יש קפיצות פתאומיות בין מצבים שונים. לדוגמה, אנחנו יודעים שאלקטרונים הנמצאים באטומים יכולים לאכלס רק אזורים מסוימים סביב הגרעין, הנקראים מסלולים אטומיים [במכניקת הקוונטים, אנו לומדים שהאלקטרונים לא מתנהגים כמו חלקיקים נקודתיים שמקיפים במסלולם את הגרעין (כמו כוכבי הלכת המקיפים את השמש) ולכן כדי לתאר אותם, משתמשים ב'פונקציית גל', שמשמעותה למעשה שהמיקום שלהם מתפרש בחלל]. בכל אחד מהמסלולים האטומיים הללו, לאלקטרונים יש כמות מסוימת של אנרגיה, שנקראת רמת אנרגיה. כשאטום משחרר אנרגיה על ידי פליטת חלקיק אור הנקרא פוטון, נראה שהאנרגיה של אלקטרון בתוך האטום עוברת מיד מרמת אנרגיה התחלתית לרמת אנרגיה נמוכה יותר. באופן דומה, כאשר אטום צובר אנרגיה על ידי קליטת פוטון, נראה שאלקטרון קופץ לפתע ממסלולו ההתחלתי למסלול סופי שבו רמת האנרגיה גבוהה יותר. למעשה, ה'קפיצות' אינן מיידיות, אך במקרים מסוימים הן אורכות זמן קצר מאוד, בסדר גודל של מיליארדית השנייה.
התיאוריה הפיזיקלית שמסבירה את העולם המופלא של האטומים והחלקיקים התת-אטומיים בצורה הטובה ביותר נקראת מכניקת הקוונטים. למרות שהיסודות של מכניקת הקוונטים הוצגו לפני כמעט מאה שנה, יש כמה חידות שעדיין לא פתרנו לגמרי, הנוגעות להתנהגות הבסיסית של החלקיקים – אבני הבניין של העולם החומרי. עם זאת, פיתחנו טכניקות רבות שעוזרות לנו להבין טוב יותר את התנהגותם של החלקיקים ולהשפיע עליהם. בהמשך המאמר נספר לכם בקצרה על שתי טכניקות כאלה – האחת מטרתה ללכוד חלקיקים (אפילו חלקיק בודד) במיקום מסוים, והשנייה מיועדת להאט את תנועתם, או לקרר אותם.
איך לוכדים הרבה חלקיקים?
חלקיקים נוטים לנוע הרבה במרחב וכשאנחנו עובדים איתם, אנחנו בדרך כלל רוצים 'ללכוד' את החלקיקים במיקום מסוים. אנחנו חוקרים לעיתים קרובות אֶלֶקְטְרוֹנִים ויונים אטומיים, שמושפעים משדות חשמליים. כשמסדרים אֶלֶקְטְרוֹדוֹת (מוליכים חשמליים) במבנים גיאומטריים מסוימים ומפעילים עליהן מתח חשמלי, ניתן לייצר שדות חשמליים הלוכדים את האלקטרונים ואת היונים במיקום מסוים [1, 2]. תוכלו לחשוב על כך כמו על גולות בקערה: החלקיקים שלנו הם הגולות, והשדות החשמליים מהווים את הקערה (איור 1A). מרכז הקערה הוא כמו מרכז ה'מלכודת' של השדה החשמלי: אם החלקיקים זזים מתחתית המלכודת (או הקערה), הם 'נדחפים' חזרה לכיוון המרכז. בדומה לכוח הכבידה שמשאיר את הגולות בתחתית הקערה, השדה החשמלי כולא את החלקיקים ליד מרכז המלכודת. הפרופסורים ווֹלְפְגָנְג פָּאוּל והָנְס דֶמֶלְט זכו יחד בפרס נובל לפיזיקה לשנת 1989 על פיתוח טכניקה של מלכודות יונים ואלקטרונים [1, 2].
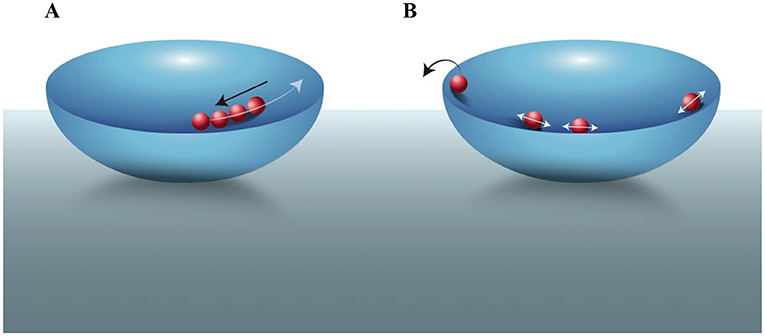
- איור 1 - לכידת חלקיקים – אנלוגיית הקערה והגולות.
- ניתן לחשוב על האלקטרונים הנעים ב'מלכודת' השדה החשמלי כעל גולות בקערה. (A) כאשר החלקיקים מתרחקים ממרכז 'קערת' השדה המגנטי (חץ לבן), הם נדחפים חזרה לכיוון המרכז (חץ שחור), כך שהם נשארים לכודים בתוך הקערה. (B) אם בכוונתנו ללכוד חלקיק בודד, אנחנו יכולים ללכוד תחילה מספר חלקיקים, ולאחר מכן להפעיל על ה'קערה' שדות חשמליים מתנודדים שמגבירים את תנועת החלקיקים. כך אנחנו 'מסלקים' חלקיקים מהקערה (חץ שחור), אחד אחרי השני, עד שנשאר בה רק חלקיק אחד [3].
איך לוכדים חלקיק בודד?
לעיתים אנחנו צריכים לשלוט בחלקיקים בצורה מדויקת מאוד. לפעמים נוח יותר לעבוד עם קבוצות חלקיקים, גם משום שנוח יותר ללכוד חלקיקים רבים יחד, וגם משום שקל יותר למדוד אותות (הזרמים החשמליים הנוצרים באלקטרודות עקב תנועת המטענים החשמליים) גדולים יותר, המיוצרים על ידי כמה חלקיקים יחד, בהשוואה לאותות קטנים יותר של חלקיק בודד. עם זאת, כשעובדים עם כמות של חלקיקים, קשה יותר לשלוט בהם באותה רמת דיוק שבה אנחנו יכולים לשלוט בחלקיק אחד, כמו שקל יותר להשגיח על ילד אחד בכיתה, לדוגמה, מאשר על כמה ילדים בו-זמנית. אתם ודאי יכולים לתאר לעצמכם שהתרחיש השני מאתגר הרבה יותר.
אנחנו יכולים לשלוט במהירותו של חלקיק בודד בדיוק רב, כמעט עד לכדי עצירה מוחלטת של תנועתו. עם זאת, קשה יותר לשלוט באותה רמת דיוק במהירותם של חלקיקים רבים בקבוצה (כאשר החלקיקים בקבוצה מתנגשים, רמות האנרגיה הפנימית שלהם יכולות להשתנות בצורה לא מבוקרת). מסיבה זו, אם אנחנו צריכים להשיג שליטה ודיוק גבוהים מאוד (כמו שנדרש בשעונים האטומיים, כפי שתראו בהמשך), עלינו לעבוד לפעמים עם חלקיקים בודדים, כדי לשלוט ברמת דיוק גבוהה בתנועת החלקיק וכדי למזער טעויות שעלולות להתרחש כשעובדים עם חלקיקים רבים [3].
כדי ללכוד חלקיק טעון אחד, אנחנו יכולים ללכוד תחילה כמה חלקיקים, כפי שמוצג באיור 1A. לאחר מכן, אנחנו יכולים להפעיל שדה חשמלי מתנודד על החלקיקים, כך שמדי פעם חלקיק 'עף' מהמלכודת. אם נחזור לאנלוגיית הקערה והגולות שלנו, אתם יכולים לדמיין שאנחנו מגבירים את תנועת הגולות שבקערה, עד שגולה אחת 'קופצת' מעבר לשפת הקערה (איור 1B). בכל פעם שחלקיק 'קופץ' מהקערה, אנחנו רואים במדידות שלנו הפחתה פתאומית ודיסקרטית של סך הזרם החשמלי המתנודד שנוצר באלקטרודות (כמו ב-[3]). אנחנו חוזרים על התהליך הזה עד שהזרם של המערכת שווה לזרם של חלקיק בודד. כך אנחנו יודעים שנשארנו רק עם חלקיק אחד במלכודת [1]. לאחר מכן, אנו יכולים לחקור את המאפיינים שלו, ו/או לרתום את המאפיינים המוכרים לנו לטובת שימושים ספציפיים [1, 2]. כשאנחנו עובדים עם יונים אטומיים מסוימים, ביכולתנו להקרין עליהם אור לייזר שמתפזר. סך הפיזור שאנחנו רואים הוא פרופורציונלי למספר היונים, וכשאנחנו בודקים אותו אנחנו יכולים לדעת מתי יש לנו יון בודד במלכודת.
איך מקררים אטומים באמצעות קרני לייזר?
עוד טכניקה חשובה המאפשרת לשלוט בחלקיקים היא האטה או קירור שלהם לטמפרטורות נמוכות מאוד באמצעות לייזרים, עד שהם בקושי זזים. טכניקה זו נקראת קירור באמצעות לייזר. כפי שלמדתם, האלקטרונים נעים סביב הגרעין רק ברמות אנרגיה מסוימות. כאשר פוטון מתקרב לאטום, הוא נבלע באטום רק אם יש לו בדיוק את כמות האנרגיה המתאימה להעברת אלקטרונים מרמת אנרגיה אחת לאחרת; אחרת, האור פשוט עובר דרך האטום. אולי אתם יודעים שהאנרגיה שהפוֹטוֹנִים נושאים קשורה ישירות לתכונה אחרת של אור, הנקראת תֶּדֶר (מספר המחזורים שגל משלים תוך שניה אחת), כך שלפוטונים בעלי אנרגיה גבוהה יותר יש תדרים גבוהים יותר, ולהיפך (מידע נוסף, באנגלית, על תדר ואנרגיה, זמין כאן).
כאשר אטום נע נגד כיוון האור, כמו זה שבקרן הלייזר, תדר האור שחווה האטום הוא בעל תדירות גבוהה יותר ולכן הוא 'אנרגטי יותר' בהשוואה למקרה שבו האטום מתרחק ממקור האור (איור 2). התופעה הזו נקראת אפקט דוֹפְּלֶר. אם נכוון את תדר הלייזר מעט מתחת לתדר (האנרגיה) הנדרש למעבר בין שני מסלולי אלקטרונים כשהאטום במנוחה, אז כשהאטום ינוע לכיוון הלייזר, הוא יחווה את תדר הלייזר כגבוה יותר והאור יבלע בו (האטום האדום באיור 2). בליעת האור מאטה את האטום בשל התֶּנַע של הפוטון המועבר לאטום. מפגש זה מפחית את המומנטום של האטום, כלומר – מאט את מהירותו. דמיינו שני שחקני רוגבי הרצים אחד לעבר השני, שההתקלות ביניהם מאטה את תנועתם. מצד שני, אם האטום נע הרחק מהלייזר (האטום הירוק ב(איור 2), התדר של קרן הלייזר שהאטום חווה נמוך יותר, והסבירות שהפוטון של קרן הלייזר ייבלע באטום יורדת. בעקבות זאת, האטום ממשיך לנוע בערך באותה מהירות (למידע נוסף, באנגלית, על קירור באמצעות לייזר, ראו סרטון זה). ההשפעה של ההפרש הזה, בין תנועת האטום לכיוון הלייזר לעומת התנועה שלו הרחק מהלייזר, משמעה שיש לנו דרך להאט אטום שנע בכיוון מסוים (לכיוון הלייזר). כשאנחנו משלבים מספר לייזרים המוקרנים מכיוונים שונים, אנחנו יכולים להאט את האטומים הנעים בכל הכיוונים.
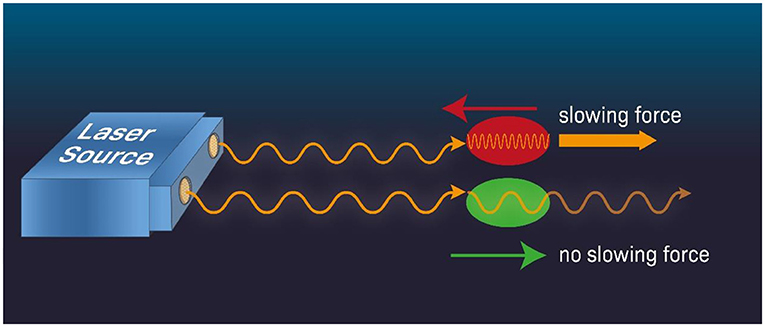
- איור 2 - קירור באמצעות לייזר.
- כאשר אטום נע נגד קרן לייזר (אדום) הוא חווה תדר גבוה יותר של הקרן (כלומר, פוטונים בתדר גבוה יותר). אם אנחנו מכוונים את תדר הלייזר מעט מתחת לתדר הספציפי שנבלע באטום כשהוא במצב מנוחה, אז לפי אפקט דופלר, האטום שנע נגד כיוון הקרן יתקל בפוטונים בתדר גבוה יותר, יבלע את אור הלייזר ויאט את הקצב. (דמיינו שפוטון הלייזר הוא כמו עצם קשה שנע לעבר האטום וכשהם מתנגשים, האטום מאט). לעומת זאת, אטום שנע באותו הכיוון של קרן הלייזר (ירוק) יבלע את פוטוני הלייזר רק במידה מוגבלת, שכן תדירות הפוטונים נמוכה מהתדר שנבלע באטום בצורה מרבית. לכן, האטום ימשיך לנוע מבלי שמהירותו תשתנה באופן ניכר. כאשר אנחנו משלבים כמה קרני לייזר המוקרנות מכיוונים שונים, אנחנו יכולים להאט את האטומים למהירויות נמוכות מאוד בכל כיווני התנועה שלהם.
שעונים אטומיים: איך יודעים מה השעה בצורה המדויקת ביותר?
שעונים כל כך נפוצים בחיי היום-יום שלנו שאנחנו כמעט ולא עוצרים לחשוב על סוגיות בסיסיות, כמו איך מודדים זמן ומה עלול להגביל את הדיוק של מדידת הזמן. מדענים ומהנדסים במעבדות דוגמת המעבדה של חטיבת הזמן והתדר של המכון הלאומי לתקנים ולטכנולוגיה בארה''ב (NIST), עוסקים בסוגיות הללו כל היום! המשימה שלהם היא להמשיך ולשפר את רמת הדיוק של השעונים, ולמדוד את הזמן בצורה יותר ויותר מדויקת. כמו רוב הפיזיקאים הניסיוניים, המדענים האלה הם ממש כמו בלשים: הם מזהים בקפידה את כל הגורמים החשובים וההשפעות הסביבתיות שבגללן אנחנו לא יכולים לדייק לגמרי בקביעת הזמן ואז הם מנסים להפחית את ההשפעות הללו ככל הניתן, כדי לשפר ללא הרף את רמת הדיוק של מדידת זמן. 'מדעני השעונים' האלה עובדים על המשימה הזו מאז שנות ה-50 של המאה ה-20; מאז שהציגו את השעונים האטומיים הראשונים (למידע נוסף על ההיסטוריה ודרך הפעולה של שעונים אטומיים, ראו מאמר זה).
באופן כללי, כדי למדוד מרווחי זמן, אנחנו מתייחסים למקור תדר מסוים וסופרים את המחזורים שלו. אנחנו יכולים לספור, למשל, תנודות של מטוטלת מכנית, או של מַתְנֵד גבישי קוורץ פְּיֶזוֹאֶלֶקְטְרִי (מכשיר שנמצא בטלפונים סלולריים. התנודות המכניות שלו נגרמות על ידי המתח החשמלי המופעל עליו). אם אנחנו יודעים מהו התדר של המקור שלנו, אפשר לספור כמה מחזורים הושלמו במרווח זמן מסוים (כלומר, המֶשֶׁךְ בין שתי נקודות בזמן), ומכך להסיק כמה זמן עבר. אנחנו יודעים כמה זמן עבר על ידי ספירה של כמה מחזורים הושלמו במרווח זמן מסוים (כלומר, משך בין שתי נקודות זמן). לדוגמה, אם אנחנו יודעים שהתדר של המקור שלנו הוא 100 הרץ (מחזורים לשנייה), אפשר להסיק שמשך כל מחזור הוא מאית (0.01) השנייה. ככל שתדר המקור גבוה יותר, אנחנו יכולים להגדיר את מרווחי הזמן בצורה מדויקת יותר.
כשאנחנו משתמשים בשעונים אטומיים כמקור התדר שלנו, ביכולתנו למדוד מרווחי זמן בצורה מדויקת מאוד. כלומר, במקום להשתמש בתדר נמוך של מטוטלת מכנית או בתדר של מתנד גבישי קוורץ, אפשר להשתמש בתדר גבוה מאוד, המתאים לתדר של אותם פוטונים הגורמים למעברים בין רמות אנרגיה דִיסְקְרֶטִיוֹת (מופרדות) של אטומים.
לדוגמה, אנחנו יכולים לשדר קרן לייזר על אטומים שהושמו במצב האנרגיה האלקטרונית הנמוכה ביותר שלהם, ולראות כמה מקרן הלייזר נבלעת בהם. כאשר קרן הלייזר נבלעת בצורה מקסימלית, אנחנו יודעים שהתדר של קרן הלייזר תואם את תדר הפוטונים. משמעות הדבר היא שאותו תדר תואם להפרש האנרגיה בין שתי רמות האנרגיה האטומית. אם קרן הלייזר לא נבלעת בצורה מקסימלית, נשנה מעט את התדר שלה עד למקסימום הקליטה, ונוודא את קיומו של תנאי זה. לאחר מכן, נספור את המחזורים של תנודת הלייזר וכך נוכל לקבוע במדויק את מרווחי הזמן (איור 3).
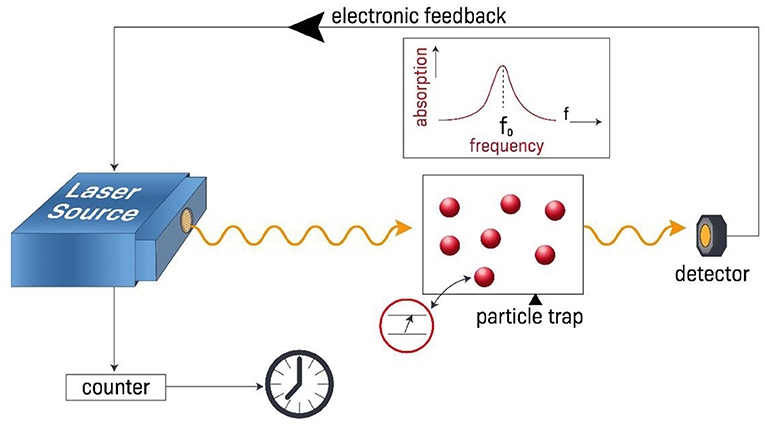
- איור 3 - עקרונות השעון האטומי.
- כאשר אטומים לכודים מקוררים (הכדורים האדומים) סופגים בצורה מקסימלית קרן לייזר, המשמעות היא שתדר הלייזר שווה לתדר הפוטונים הנדרש ל'הקפצה' של אלקטרונים מרמת אנרגיה נמוכה לרמת אנרגיה גבוהה יותר (התרשים שבעיגול האדום). אנחנו מכוונים את תדר הלייזר באמצעות מערכת המספקת משוב אלקטרוני, עד שקרן הלייזר נבלעת בצורה מקסימלית באטומים. לאחר מכן אנחנו משתמשים במכשיר שסופר כמה מחזורים קרן הלייזר משלימה. אז אנחנו משתמשים בתוצאה, יחד עם תדר המעבר של האטום, כדי לחשב כמה זמן עבר. מכיוון שללייזר יש תדר גבוה מאוד, הזמן לכל מחזור תנודות הוא קצר מאוד, לכן אנחנו יכולים למדוד מרווחי זמן ברמת דיוק גבוהה מאוד.Laser source = מקור הלייזר Particle trap = מלכודת חלקיקים Absorption = בליעה Frequency = תדר Detector = גלאי Electronic feedback = משוב אלקטרוני Counter = מוֹנֶה.
נעשה שימוש בשעונים האטומיים בלוויינים, לדוגמה, כדי לאתר את מיקומכם דרך מערכת האיכון (GPS) שבטלפונים החכמים. עושים זאת על ידי מדידה באמצעות שעונים אטומיים מסונכרנים של הזמן שלוקח לאור (מהירות האור היא נתון ידוע) לנוע מהלוויין לטלפונים החכמים שלכם. אז, ניתן להשתמש בתוכנה כדי לחשב את המרחק המדויק שלכם מהלוויין. באמצעות רשת של לוויינים מסונכרנים בזמן, ניתן לקבוע את המיקום התלת ממדי שלכם. השעונים האטומיים בלוויינים חייבים להיות מדויקים מאוד, שכן טעויות קטנות מאוד במדידת הזמן שלהם, אפילו בקנה מידה של מיליונית השנייה, גורמות לשגיאות גדולות של מאות מטרים בקביעת מיקומכם באמצעות מערכת האיכון.
במשך שנים רבות, השעונים האטומיים הטובים ביותר התבססו על מעבר מסוים המתרחש ביסוד כימי ספציפי (מעבר גלי המיקרו ה'על-דקים' (hyperfine) באטומים ניטרליים של היסוד צֶסיוּם, בעלי תדר של כ-9.2 גיגה-הרץ, שהם כ-9.2 X 109 הרץ). בשנים האחרונות, תקני התדר המדויקים ביותר מתבססים על מעברים שיש להם תדרים קרובים לאלו של גלי אור התואמים לצבעי האור שאנחנו יכולים לראות – בסביבות 1015 מחזורים לשנייה [4] (למידע נוסף על שעונים אטומיים אופטיים, ראו מאמר זה). חוסר הדיוק בתדרים אלה עקב הפרעות סביבתיות הוא בערך 1 חלקי 1018, מה שאומר ששעונים המבוססים על מעברים אלה 'יזייפו' בפחות משנייה על פני פרק זמן שקרוב לגיל היקום (בערך 13.7 מיליארד שנים).
ניתן לרתום את הטכניקות המתקדמות של קירור באמצעות לייזר ליישומים אפשריים חשובים. אחד מהם נקרא מִחְשוּב קוונטי. ביישום זה, משתמשים במאפיינים הקוונטיים של אטומים ושל יונים או באמצעים מַקְרוֹסְקוֹפִּיים כדי לבצע סוג מסוים של חישובים מורכבים ביעילות רבה יותר מאשר במחשבים דיגיטליים 'רגילים'. כדי להבין קצת יותר תוכלו לעיין בנספח שבהמשך.
המלצות למוחות צעירים
מבחינתנו, העבודה שאנחנו עושים היא יותר כמו תחביב, כי גם אם לא היינו עוסקים במקצוע הזה, כנראה שהיינו מתעניינים באותם התחומים. זה מה שאנחנו מאחלים גם לכם. אנחנו מאמינים שכדאי לכם למצוא משהו שאתם אוהבים באמת – כך תהיו מוכנים לעבוד קשה ולהשקיע בו זמן רב, וסביר להניח שתזכו להצלחה. גם אם תשנו את דעתכם לגבי מה שאתם אוהבים או לגבי מה שמעניין אותכם, זה בסדר. כמובן שאין צורך לבזבז את הזמן על משהו שלא כל כך קשור למה שאתם אוהבים. לדעתנו חשוב גם לראות את המציאות כפי שהיא ולהתאים את החלטותיכם לרצונותיכם בעת הצורך.
לאלו מכם שבוחרים בקריירה מדעית, חשוב גם לדעת שצריך סבלנות ויכולת התמדה. במדע, ובמיוחד במחקר מדעי, מאמצים לרוב לא יניבו פרי באופן מיידי. לוקח זמן לפתח את הידע והמיומנויות הנדרשות לביצוע מחקר באיכות גבוהה, ולהגיע לתובנות חדשות על העולם. עליכם לפתח יכולת לעמוד בקשיים ולהתמיד בעבודה גם כשהדברים לא קורים כפי שתכננתם. אם תעשו זאת, בסופו של דבר עבודתכם תניב פרי ותוכלו ליהנות מנפלאות הגילוי.
אנחנו רוצים גם להדגיש שלדעתנו, אין זה נכון לבחור בקריירה או במסלול מסוימים רק כי אתם מצפים להרוויח מהם כסף. לא סביר שתהיו מאוד מרוצים או שתצליחו במיוחד אם תתמקדו רק בצורך הכלכלי. בדומה לכך, אם תשקיעו את מרצכם במרדף אחר פרסים, סביר להניח שגם זו לא תהיה דרך מוצלחת במיוחד. אנחנו ממליצים לבחור משהו שאתם אוהבים ולהשקיע בעבודה קשה שתקדם אתכם לעבר מטרה משמעותית, במקום להתמקד בשכר או בהכרה מצד הסביבה.
לסיום, יש לנו עצה לאלו מבינכם שמתכוונים ללמוד תואר אקדמי. אם תמשיכו ללימודי התואר השני והשלישי, ישבצו אתכם לעבודה על פרויקט מסוים. מניסיוננו, עדיף תמיד לא להתמקד בנושא המדויק שעליו אתם עובדים, אלא גם 'להתפזר' קצת ולקרוא חומרים קשורים, אך רחבים יותר. כך בדיוק עלה במוחו של דיוויד הרעיון לקירור באמצעות לייזר – הוא קרא מאמרים נוספים בנושאים שלא היו קשורים ישירות לפרויקט שלו באותה תקופה. בסופו של דבר, אותו הרעיון הפך לאבן דרך מרכזית בקריירה המדעית שלו.
נספח: פיתוחים ושימושים עתידיים
הביצועים של השעונים האטומיים ימשיכו להשתפר. יש לחדד את התייחסותנו לשינויים בתדר עקב הפרעות סביבתיות רבות המשפיעות על האטומים, כגון שדות חשמליים ומגנטיים מקומיים מזדמנים. ישנן שתי השפעות נוספות שעלינו לכלול בהשוואות בין השעונים. מקורן בתורת היחסות של איינשטיין והן צורות נפרדות של מה שנקרא 'הרחבת זמן' – זוהי תופעה של האטת הזמן במערכת ייחוס אחת ביחס לאחרת.
ראשית, איינשטיין לימד אותנו שבמערכת ייחוס שנעה ביחס אלינו, לדוגמה, המערכת הקשורה לאטום או ליון הנמצאים בתנועה, הזמן נע לאט יותר בהשוואה אלינו, כצופים נייחים במעבדה. הסחה (סטייה) זו היא פרופורציונלית לאנרגיית התנועה הממוצעת של היונים, כך שאחד היתרונות של קירור באמצעות לייזר הוא שאנחנו יכולים להפחית את התזוזה בפקטור של כמיליון בהשוואה ליונים או לאטומים בטמפרטורת החדר.
העיקרון השני של הרחבת זמן שאותו למדנו מאיינשטיין הוא שהזמן נע לאט יותר בנוכחות כוח הכבידה [הידוע בתור 'הסחה כבידתית פוטנציאלית לאדום' [5–7]]. אין לכך השפעה גדולה על החוויה היום-יומית הרגילה שלנו, כפי שניתן להמחיש בדוגמה הבאה: נניח שאת או אתה, הופרדתם בלידתכם מתאום או תאומה. אתם חיים בגובה פני הים; התאומה או התאום שלכם חיים בגובה של 1.6 ק''מ מעל פני הים (בבולדר, קולורדו שבארה''ב, לדוגמה). אחרי 80 שנה, התאומה או התאום שלכם יהיו מבוגרים מכם בכ-0.001 שניות בלבד.
זוהי כמובן השפעה זניחה מבחינת פעילויות אנושיות טיפוסיות, אך ניתן לצפות בה בשעונים מדויקים ויש לקחת אותה בחשבון כשמשווים בין שעונים במקומות שונים, כמו במקרה של ניווט באמצעות GPS.
הנה דוגמה פשוטה של השפעה זו: במכון הלאומי לתקנים וטכנולוגיה בבולדר, קולורדו, ערכו השוואה בין שני שעונים נפרדים, המבוססים על אותו מעבר אטומי ביוֹן [5]. תחילה, שני השעונים מוקמו באותו גובה, אך במרחק של כמה מטרים אחד מהשני. הסטייה ביחס התדרים של שני השעונים הייתה שווה ל1 חלקי1018. לאחר מכן, הגביהו את אחד השעונים ב-33 ס''מ ומדדו שוב את יחס התדרים של שני השעונים. תדר השעון המוגבה עלה בכ-4 חלקי1017, קרוב לתוצאה הצפויה.
דוגמאות דרמטיות אף יותר של ההסחה הכבידתית הפוטנציאלית לאדום הוצגו לאחרונה על ידי שתי קבוצות המשתמשות באטומים ניטרליים שבהם ההסחה הכבידתית לאדום נצפתה בקנה מידה של מילימטרים [6, 7].
בנוסף לשעונים משופרים, עוד שימוש פוטנציאלי חשוב המבוסס על שליטה ומניפולציה של מערכות קוונטיות בודדות הוא עיבוד מידע קוונטי, הכולל חישוב קוונטי (חישובים המבוצעים על ידי מחשב באמצעות אלמנטים קוונטיים) וסימולציה קוונטית (סימולציות ממוחשבות המשתמשות באפקטים קוונטיים להבנת תופעות פיזיקליות). למרות שנושא זה הוא מעבר למסגרת המאמר, אנחנו יכולים לתאר לכם בקצרה את התחום החשוב הזה ואת כיווני ההתפתחות העתידיים שלו.
לשם כך, ראשית עלינו להציג לכם עוד תופעה מוזרה בעולם החלקיקים הקוונטיים, הנקראת סוּפֶּרפּוֹזִיצְיָה. סופרפוזיציה מתייחסת לעובדה שחלקיקים יכולים לייצג שתי רמות אנרגיה שונות בו-זמנית. נשתמש שוב בהשוואה בין היון הלכוד הבודד לבין הגולה בקערה. אנחנו יכולים לעורר את תנועת היון עם שדה חשמלי מתנודד וליצור מצב 'רגיל' שבו הגולה מתגלגלת קדימה ואחורה בתוך הקערה, למשל בין הצד השמאלי לבין צד הימני שלה. עם זאת, באמצעות הכלים הקוונטיים שלנו, אנחנו יכולים גם ליצור מצב שבו בזמנים מסוימים הגולה נמצאת בו-זמנית גם בצד שמאל וגם בצד ימין של הקערה – כלומר, במצב 'סוּפֶּרפּוֹזִיצְיָה'. זה מאוד מנוגד לאינטואיציה ולא הגיוני בעולם היום-יומי ה'רגיל' שלנו, אבל זה העולם שבו חיים מדעני הקוונטים.
אם נרחיב את הרעיון הזה ונחיל אותו על רמות האנרגיה של אטום בודד, נוכל ליצור מצב סופרפוזיציה שבו האטום נמצא בו-זמנית במצב האנרגיה הנמוך והגבוה יותר שלו. בפועל, קל יחסית לעשות זאת. בעבר דיברנו על יון אטומי בודד שסופג פוטון בודד ועובר מרמת האנרגיה הנמוכה שלו לרמת אנרגיה גבוהה יותר. מסתבר שכאשר קרן הלייזר שלנו מורכבת מפוטונים רבים הפרוסים בחלל לכל הכיוונים בניצב לכיוון הקרן, ואנחנו מפעילים את הלייזר למשך זמן מסוים, אנחנו יכולים לממש מצב בו האטום רק חצי מְעוֹרָר (בעל אנרגיה גבוהה יותר). כלומר, לאחר שמכבים את קרן הלייזר, האטום נמצא בסופרפוזיציה של רמת האנרגיה האלקטרונית הנמוכה שלו ורמת האנרגיה הגבוהה שלו. כפי שניתן לראות בדוגמה זו, סופרפוזיציה פירושה שחלקיק יכול להתקיים בו-זמנית במספר מצבים בכל רגע נתון.
תחום החישוב הקוונטי מבוסס בחלקו על סופרפוזיציה של שני מצבים של מערכת קוונטית, כמו היונים האטומיים בדוגמה שלעיל. אולי אתם יודעים שמחשב רגיל מורכב מיחידות בסיסיות הנקראות 'בִּיטִים'. הביטים יכולים להיות באחד משני מצבים, אנחנו להם קוראים '0' ו-'1'. כאשר משלבים את המערכת הדואלית הזו עם מערכות דואליות דומות, ניתן לבצע את כל החישובים של מחשב רגיל. הרעיון של המחשב הקוונטי הוא שכל יחידה בסיסית, המכונה 'קיוּבִּיט' (קיצור של ביט קוונטי) יכולה להיות בסופרפוזיציה של מצבים, כלומר, במספר מצבים בו-זמנית.
כדי לייצג את המצב של קיוביט כסופרפוזיציה של המצבים הקוונטיים '0' ו-'1', אנחנו משתמשים לעתים קרובות בסימונים '〉1|' ו- '〉0|'. כך אנחנו מבטאים את מצב הסופרפוזיציה הכללית של הקיוביט: 〈1|β+ 〈0|α, כאשר α|2| היא ההסתברות למדוד קיוביט במצב '0', ו- β|2| היא ההסתברות למדוד קיוביט במצב '1'. כאשר ההסתברויות הללו שוות, אנחנו קוראים לזה 'סופרפוזיציה שווה של מצבים'.
במסגרת זו, אחד ממצבי הסופרפוזיציה האפשריים של הקיוביט יכולה להיות
, כאשר .
כעת, בואו נראה מה קורה במערכת גדולה יותר. אם אנחנו בוחנים מערכת 'רגילה' של שני ביטים כאשר כל אחד מהם יכול להיות במצב '0' או '1', אנחנו יכולים לייצג סכום של 22 = 4 מספרים. המספרים הללו הם: 01 ,10 ,00 ו-11. המצב הכללי של מערכת מקבילה של שני קיוביטים הוא α|00〉 + β|01〉 + γ |10〉 + δ|11〉, בעוד שההסתברות למדוד את המצבים 〈11|, 〈10|, 〈01|, ו- 〈00| היא |α|2 ,|β|2, |γ|2 -ו |δ|2, בהתאמה. אחת הדוגמאות לסופרפוזיציה של ארבעת המצבים תהיה המצב . עם הסתברות מדידה של עבור כל מצב. כפי שאתם יכולים לראות, סופרפוזיציה של מערכת של שני קיוביטים מכילה (או כפי שאנחנו אומרים, 'מאחסנת'), ארבעה (22) מספרים בעלי שני ביטים בו-זמנית. בניגוד לכך, מערכת 'רגילה' של שני ביטים יכולה לאחסן רק מספר אחד בזמן נתון (00, 10, 01, או 11).
כאשר מחילים זאת על מערכות גדולות אף יותר, אפשר לראות שמערכת 'רגילה' המכילה מספר ביטים מסוים (הנקראת מערכת n-bit), יכולה לאחסן מספר מסוים (n) של זוגות ביטים (המורכבים מביטים של '0' ושל '1'). עם זאת, סופרפוזיציה של מספר מסוים (n) של קיוביטים, יכולה לאחסן 2n מספרים בעלי n ביטים בבת אחת (כלומר פי 2n יותר מספרים בהשוואה למערכת 'רגילה' באותו גודל). זה מעיד על כך שכאשר אנחנו מבצעים פעולה על אחד מהקיוביטים בסופרפוזיציה שלנו, של -qubitn, אנחנו מבצעים את הפעולה על כל 2n המצבים של n קיוביטים בו-זמנית. כלומר, מחשב קוונטי יכול לאחסן ולעבד כמות הרבה יותר גדולה של מידע מאשר מחשב 'רגיל' באותו גודל. זוהי דוגמה ל'קנה מידה מעריכי' (כלומר, שמעלים אותו בחזקה). חשבו על ההפרש העצום! אם יש לנו 300 קיוביטים למשל, אנחנו יכולים לאחסן בו-זמנית 2300 מספרים בעלי 300 ביטים. זיכרון 'רגיל' בגודל כזה ידרוש יותר חלקיקים משקיימים ביקום! קל יחסית ליצור מצב כזה עם יונים לכודים, אך קשה הרבה יותר ליצור שערים לוגיים שימושיים למערכת בגודל כזה. [יישום של שערים לוגיים קוונטיים הוא מעבר לתחום של מאמר זה, אך אתם יכולים לקרוא על כמה מהרעיונות הבסיסיים ב-[8]].
באופן עקרוני, מחשבים קוונטיים יכולים להיות הרבה יותר יעילים ומהירים ממחשבים 'רגילים' עבור בעיות מסוימות, ויכולים לפתור בעיות שהמחשבים הקונבנציונליים הנוכחיים אינם מסוגלים לפתור. מעבר לפירוק יעיל של מספרים לגורמים (כפי שהציע פיטר שור), אחד השימושים הצפויים של המחשבים הקוונטיים הוא היכולת לדמות דינמיקה או התנהגויות של מערכות קוונטיות מורכבות. באמצעותו יהיה ניתן, לדוגמה, לדמות את פעולתן של מולקולות בחומר כימי המיועד לשמש בטיפולים רפואיים ולחקור אותן באמצעות הדמיות ממוחשבות ללא צורך לסנתז אותן במעבדה. סימולציות דומות יכולות גם ללמד אותנו דברים חדשים על פיזיקה, או לפתור בעיות פיזיקליות מסובכות שמחשבים 'רגילים' לא יכולים לפתור.
אנשים רבים תוהים מתי ייבנה המחשב הקוונטי הראשון. התשובה היא שכבר יש לנו מחשבים קוונטיים, אבל נכון לעכשיו, מחשבים 'רגילים' מסוגלים לפתור את הבעיות שגם הם פותרים (למרות שאולי לא באותה יעילות), או שהבעיות שהם פותרים אינן מעניינות מבחינה פרקטית. כנראה שבנייה ושיפור של המחשבים הקוונטיים יתרחשו בהדרגה – המחשבים הקוונטיים הראשונים יוכלו לפתור רק בעיות 'מעניינות' פשוטות, אך ככל שהתחום יתקדם, הם יוכלו לעשות דברים מורכבים יותר. אולי בעשר השנים הבאות נוכל לרתום את המחשבים הקוונטיים לדברים שימושיים, כמו לגילוי של משהו שלא ידענו קודם, או להדמיית מערכת מעניינת שיהיה לה יישום מעשי. יש לנו למה לצפות!
חומרים נוספים
כאן תוכלו לקרוא את תַּעְתִּיק הריאיון שנערך בין פרופ' דיוויד וינלנד לבין נועה שגב.
מילון מונחים
רמת האנרגיה (Energy level): ↑ ערך אנרגטי דִיסְקְרֶטִי (בָּדִיד) אפשרי של מערכת קוונטית, כמו של אלקטרונים באטום.
מכניקת הקוונטים (Quantum Mechanics): ↑ תיאוריה בפיזיקה המתארת התנהגות ואיכויות של אטומים ושל חלקיקים שונים, כמו גם של מערכות מַקְרוֹסְקוֹפִּיות יותר, כמו וִיבְּרַצְיוֹת (תנודות) של מַתְנֵדִים מכניים זעירים.
אֶלֶקְטְרוֹנִים (Electrons): ↑ חלקיקי יסוד באטום בעלי מטען שלילי.
אֶלֶקְטְרוֹדוֹת (Electrodes): ↑ מבנים העשויים בדרך כלל ממתכת המוליכים חשמל ויכולים לשמש ליצירת שדות חשמליים.
קירור באמצעות לייזר (Laser Cooling): ↑ טכניקה להאטת תנועתם של אטומים ושל יונים באמצעות קרני לייזר.
פוֹטוֹנִים (Photons): ↑ חלקיקי אור שנושאים כמות ספציפית ודיסקרטית של אנרגיה, התואמת את התדר שלהם. רעיון זה הוצע על ידי מקס פְּלָאנְק ואומץ לאחר מכן על ידי אלברט איינשטיין.
תֶּנַע (מוֹמֶנְטוּם) (Momentum): ↑ גודל פיזיקלי המוגדר כתוצר של מסת החלקיק ושל מהירותו. ככל שיש לחלקיק יותר תנע, כך הכוח שהוא יכול להפעיל על חלקיקים אחרים גדול יותר.
הצהרת ניגוד אינטרסים
הכותבת NS מצהירה שהייתה מועסקת של פרונטירז בזמן הגשת המאמר. לא הייתה לכך השפעה על תהליך ביקורת העמיתים ועל ההחלטה הסופית.
המחברים מצהירים כל המחקר נערך בהעדר כי קשר מסחרי או פיננסי שיכול להתפרש כניגוד אינטרסים פוטנציאלי.
תודות
ברצוננו להודות לשרון עמלני עבור האיורים במאמר זה.
מקורות
[1] ↑ Paul, W. 1990. Electromagnetic traps for charged and neutral particles. Rev. Modern Phys. 62:531. doi: 10.1103/RevModPhys.62.531
[2] ↑ Dehmelt, H. 1990. Experiments with an isolated subatomic particle at rest. Rev. Modern Phys. 62:525. doi: 10.1103/RevModPhys.62.525
[3] ↑ Wineland, D., Ekstrom, P., and Dehmelt, H. 1973. Monoelectron oscillator. Phys. Rev. Lett. 31:1279. doi: 10.1103/PhysRevLett.31.1279
[4] ↑ Diddams, S. A., Bergquist, J. C., Jefferts, S. R., and Oates, C. W. 2004. Standards of time and frequency at the outset of the 21st century. Science. 306:1318–24. doi: 10.1126/science.1102330
[5] ↑ Chou, C. W., Hume, D. B., Rosenband, T., and Wineland, D. J. 2010. Optical clocks and relativity. Science. 329:1630–3. doi: 10.1126/science.1192720
[6] ↑ Bothwell, T., Kennedy, C. J., Aeppli, A., Kedar, D., Robinson, J. M., Oelker, E., et al. 2022. Resolving the gravitational redshift across a millimetre-scale atomic sample. Nature. 602:420–4. doi: 10.1038/s41586-021-04349-7
[7] ↑ Zheng, X., Dolde, J., Lochab, V., Merriman, B. N., Li, H., and Kolkowitz, S. 2022. Differential clock comparisons with a multiplexed optical lattice clock. Nature. 602:425–30. doi: 10.1038/s41586-021-04344-y
[8] ↑ Monroe, C. R., and Wineland, D. J. 2008. Quantum computing with ions. Sci. Am. 299:64–71. Available online at: https://www.scientificamerican.com/article/quantum-computing-with-ions/
