Abstract
Mathematics is the most logical and unbiased scientific field there is. What is true in mathematics today will forever stay true, and mathematical arguments will always clearly indicate which side “wins”. These are some of the characteristics of mathematics that I have liked very much since I was young. In this article, I will try to demonstrate the beauty of mathematics and show you that it appears in many situations in our daily lives—including places we might not expect. Then, I will give you a taste of two studies I conducted in a mathematical field called combinatorics, and I will explain how they are related to everyday problems. One of these problems is how to perform accurate mathematical analyses of large streams of data that we cannot save in a computer’s memory. Finally, I will try to give you an idea of my life as a mathematician—the challenges and difficulties, alongside the immense enjoyment and satisfaction I derive from them. Join me to an extended dive into my work on the wonders of combinatorics.
Professor Noga Alon was awarded the 2005 Gödel Prize, jointly with Prof. Yossi Matias and Prof. Mario Szegedy, for the work that laid the foundations of the analysis of data streams using limited memory. In 2022, Prof. Alon was awarded the Shaw Prize in Mathematical Sciences, jointly with Prof. Ehud Hrushovski, for their remarkable contributions to discrete mathematics and model theory with interaction notably with algebraic geometry, topology, and computer sciences.
Introduction to the Beauty of Mathematics
Mathematics is an academic discipline that can provoke strong feelings —some people love it, and some people hate it. Some of the people who love math recognize that love from a very young age. For example, I knew from the age of 8 or 9 that I wanted to be a mathematician. I do not think that everyone should like mathematics or be mathematicians (in fact, I do not think that humanity would do very well if most people were mathematicians). Still, mathematics contains much beauty, and I think that everyone can learn to see and appreciate it—from close up or from further away.
For me, mathematics is primarily a logical and objective way of thinking, with which I try to understand various types of processes. One of the things I especially like about mathematics is its objectivity. In mathematical arguments, one side can convince the other side that its argument is right, and the other side will actually be convinced by the mathematics itself. This does not normally occur in other situations in which there is a difference of opinions. For example, think about political arguments—it is very rare for one side to convince the other side to change its mind. Mathematics also has a dimension of stability to it—what is true now will always stay true; and what is untrue will forever stay untrue. In other scientific disciplines, including physics, this is not necessarily true—theories describing reality may, and often do, change throughout time.
I also like the challenge that mathematics holds. As a mathematician, I try to solve puzzles. Sometimes, I know in advance that the puzzle has a solution and I try to find it. For other puzzles, I am not even sure that a solution exists. When encountering a puzzle, I quite often feel that I have no chance of solving it. But then I think about it a lot, try various strategies, and I suddenly experience an insight. I do not always know what sparked the insight, or why it happened when it did—sometimes half an hour after I start thinking about the problem, and other times months later—but suddenly I know something new that I did not know beforehand. I find this process of deciphering mathematical challenges very satisfactory.
Sometimes I even think of mathematics as an art because it has a special beauty. There are practical parts of mathematics that are used in other scientific disciplines such as physics, chemistry, and biology, to explain our reality. Other parts of mathematics are more abstract and contain mathematical structures that do not necessarily have any direct connection to the reality we are familiar with; or sometimes such connections are only realized much later. However, in my view, the value of mathematics is independent from whether it describes something in our reality. Like abstract art, which does not deal with concrete physical objects but is nonetheless pleasant to look at, abstract math has its own beauty.
Math Appears in Surprising Places
Mathematics is not limited to problems we solve on paper in algebra and geometry classes. Often, it appears in the midst of everyday phenomena. As an example, let me tell you the story of a Hungarian sociologist named Sandor Szalai, who lived in the twentieth century. Szalai conducted experiments on friendships between children. He asked every pair of children whether they were friends, where the relation was symmetric (meaning that both members of the pair said they were friends or both said they were not friends; there was no situation in which one said “yes” and the other said ”no”). Szalai discovered that, each time there were at least 18 children in a group, there were always four children for which each pair (six pairs overall) were all friends, or not friends. Szalai thought this was a new and exciting sociological discovery. But, after talking to his mathematician colleagues, it became clear that this was not a sociological discovery but rather a mathematical fact! The situation Szalai was studying is a special case of a mathematical theory called Ramsey’s theorem. Ramsey’s theorem claims that, in general situations, it is not possible to have complete disorder—every system that is large enough contains a sub-system that is very organized.
Using our example, we can represent every kid as a dot on paper, and connect every two dots with a blue line to represent a friendship, or a red line to represent no friendship. In a group of 18 children, we will get 18 points among which every two points are connected by a blue or a red line. According to Ramsey’s theorem, no matter how we color these lines, there will always be four dots for which all the lines are colored in red or four dots for which all lines are colored in blue. So, this result is a mathematical one, not a sociological one.
Try to see what happens in a similar situation with six children. Connect every pair of six dots on paper using blue and red lines. You will find that, no matter which color lines you use, you will get a blue triangle or a red triangle, or both blue and red triangles (Figure 1). The curious amongst you can try to prove that, if you take five children, this is not the case—you do not always end up with a blue or a red triangle.

- Figure 1 - Social mathematics.
- If we look at six children, for which every pair can be friends (blue line) or not friends (red line), we will necessarily get three children that are all friends (blue triangle) and/or three children that are not friends (red triangle). This is a mathematical result that influences social structures.
Combinatorics—Two Examples on Thieves and Forgetters
One of the main mathematical fields I study is called combinatorics. Combinatorics is the mathematics of finite structures (opposed to continuous mathematics, which deals with infinite structures) [1]. For simplicity, think about these structures as collections of objects. In combinatorics, we deal with finite groups of objects and we try to understand their properties. In the previous example of the children, a group is the collection of all points (children), some of which are connected with blue lines and others with red lines. Classical combinatorics deals with questions like: how many ways are there to organize 10 children if we line them up one next to the other in one line? Or: how many options are there to choose 10 children out of a group of 50? We can also ask more complex questions, like: can we choose seven triples from a group of seven children, such that every possible pair of triples will have exactly one shared kid between them, and every two kids in the group will be contained in exactly one triple? Another example of a combinatorial question on a structure that you might know is related to Sudoku. We could, for example, ask how many possible unique Sudoku games could be made for 30 × 30 Sudoku board?
In modern combinatorics, we often deal with problems in which we must determine the largest or smallest size of a combinatorial structure that satisfies certain properties. These questions have many applications in computer science, and in other areas of mathematics, such as geometry and number theory.
Combinatorics Example 1: Fair Thieves
One of the problems I delved into in my career deals with the fair splitting of a necklace. Think of a situation in which two (mathematically skilled) thieves steal a necklace with two types of gems—diamonds and rubies (Figure 2). These thieves are fair, and they decide that they will each receive an equal number of diamonds and rubies. To distribute their treasure, they want to cut the necklace using the fewest possible cuts. What is the smallest number of cuts they must perform to split the necklace fairly between them?

- Figure 2 - Fair splitting of a necklace made of diamonds and rubies.
- Let us assume that two thieves are stealing a necklace made of diamonds and rubies, and they want to split the treasure evenly. What is the least number of cuts they could perform to split the treasure equally? Can you see that, in this example, one cut is sufficient?
If all the diamonds are located on one side of the necklace and all the rubies are on the other side, it is easy to see that two cuts are enough to split the treasure equally (Figure 3A). Now we will prove that, even if the gems are arranged randomly in the necklace, two cuts are still sufficient to split the treasure fairly. Let us assume that the necklace contains eight diamonds and six rubies. For a fair split, each thief must receive four diamonds and three rubies.
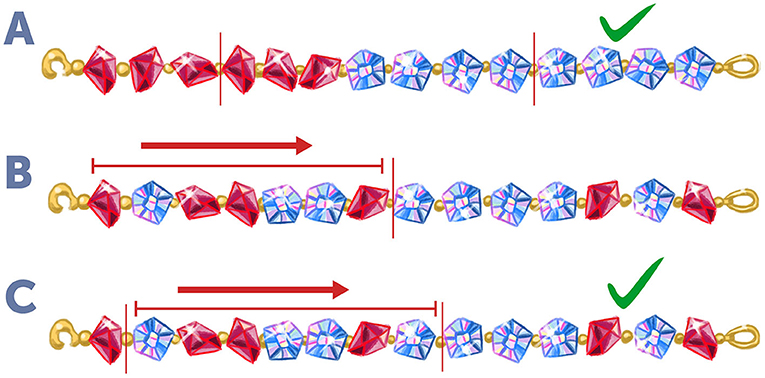
- Figure 3 - Fair splitting of a necklace with two types of gems.
- (A) If a necklace has six rubies on the left and eight diamonds on the right, it is easy to see that two cuts (red vertical lines) are sufficient to split the necklace fairly. (B) If the same gems were randomly organized, one cut in the middle creates a situation in which there are too many rubies and too few diamonds on the left, and too few rubies and too many diamonds on the right. (C) If we shift the cut one gem to the right and add another cut after the first gem from the left, we add one diamond and remove one ruby from the middle section. In this situation, both sections contain three rubies and four diamonds. Thus, even for a randomly organized necklace, two cuts are sufficient to split the gems equally between two people.
We will start with a situation in which the diamonds and rubies are randomly organized along the necklace (Figure 3B). First, we will cut the necklace in the middle and notice that we have too many rubies on the left side (four gems), and too few rubies on the right side (two gems). But if we shift our cut section one place to the right, we will gain one diamond from the right and lose one ruby from the left (Figure 3C). If we count the number of stones between the two red lines (the first thief’s treasure) and outside the two red lines (the second thief’s treasure), we will see that in both cases there is an equal number of gems: four diamonds and three rubies. Thus, we succeeded at splitting the necklace fairly using two cuts!
Now we will look at an example of a necklace with an equal number of gems of each type, organized randomly. We first choose a cut section between the end and the middle of the necklace (as in Figure 3B). Each time we shift our cut section to the right, we lose one gem on the left and gain one gem on the right, because the number of gems in both pieces of the necklace should stay equal. One of four options will happen when we shift the cut section:
- We will lose a ruby on the left and gain a ruby on the right;
- We will lose a diamond on the left and gain a diamond on the right (in both 1 and 2 the number of rubies in the cutting section will not change);
- We will lose a ruby on the left and gain a diamond on the right (we will have one less ruby than we had before the shift); or
- We will lose a diamond on the left and gain a ruby on the right (we will have one more ruby than we had before the shift).
You can see that, in each case, the number of rubies we have can change only by one after the shift. If we start from a situation in which we have too many rubies on the left side of the necklace, and we shift the cut section all the way to the right side of the necklace, we will inevitably end up with too few rubies—because we are back to the initial situation, in which we had too many rubies on the left and too few rubies on the right. If we start from a situation in which we have too many rubies on one side and end in a situation in which we have too few rubies on that side, when we change the situation by no more than one ruby each time, then surely at some point along the way the number of rubies on both sides will be equal (which will also make the number of diamonds equal on both sides). This is the result of a mathematical theorem called the discrete intermediate value theorem, which states that if something starts with a value that is too high, ends with a value that is too low, and shifts only a little bit each time, then along the way we will inevitably get the desired value.
For the general case of the same problem, we can think about some number of thieves, which we will call “k,” and some number of gem types, which we will call “t.” I proved that, in every case in which we want to split a necklace with t types of gems equally between k thieves, it is sufficient to perform (k – 1) • t cuts to split the treasure fairly [2]. In the simple case we previously saw, there were k = 2 thieves and t = 2 types of gems, and we could split the treasure using (2 – 1) • 2 = 2 cuts. In the same way, if there were four thieves and two types of gems, we could split the treasure fairly using (4 – 1) • 2 = 6 cuts (A more detailed example of the case of four thieves and two gem types, and a further explanation of the proof for the general case can be seen in this video). It is important to understand that the proof for the general case is complex. It is not derived simply and directly from the proof used for the cases of two or four thieves. This is often the case in mathematics—it is not enough to think logically and make intelligent claims; we must also use methods and tools that require a lot of knowledge and understanding. In our case, the proof for fairly splitting a necklace requires the use of advanced mathematical methods, including tools from a mathematical field called topology.
The problem I described using the fair splitting of a necklace also applies to everyday situations. For example, think about cutting a long cake that has various parts—chocolate, sweets, and other surprises—and we want to split it among several people such that each will get the same components of the cake. Or, we can think about a situation in which a piece of land must be split between several people, and the land has a mixture of uses (agricultural land, natural land, and land for construction). In this case, we want each person to get the biggest possible plot of land while also equally dividing up the land in terms of usage types.
Splitting of resources is another example. In this case, we might have a collection of resources to be split between people, but each person has a unique preference and opinion about the value of each resource. Our aim is to split the resources between the people such that everyone feels like they received an equal share. For example, one person will get the share of resources they prefer, which might be undesirable to another person. In this way, no one will envy the others, and everyone will be pleased about what they got. These questions, among others, are studied using a mathematical area called algorithmic game theory.
Combinatorics Example 2: Sophisticated Forgetters
Another problem I studied is an interesting issue in computer science, related to algorithms for dealing with data streams. In such cases, we receive a large collection of data, so big that we cannot save it in a computers’ memory, but can only read it as it passes through the computer. One of the questions I studied was: which statistical properties of these data can we know, despite not being able to save it [3]? Without saving the data, there are some things we can know about it and other things we cannot know—and this is not always evident at first glance. Here is an example: I will tell you all the numbers between 1 and 100 in a random order, except one number, which I will omit on purpose. You cannot write the numbers down as I say them, and you will not be able to remember all of them. Is there a way that you could tell me which number I omitted, without remembering the numbers themselves? Take some time to think about this.
The answer is yes—you can find out which number was omitted without remembering all the numbers. Here is how: for every number I tell you, add it to the previous number I mentioned, and you will get a sum. If I tell you 7 and then 8, you sum 7 + 8 and remember 15. Then I tell you 22, you add it to 15, and remember 37, and so on. At the end of this process, you will get the sum of all the numbers I told you. You can subtract this sum from the sum of all the numbers between 1 and 100 [which you can calculate relatively easily as the sum of 50 pairs, each having a value of 101 (100 + 1, 99 + 2, 98 + 3, … 50 + 51)]. This means the sum of all numbers from 1 to 100 is 50 • 101 = 5,050. The difference you get when you subtract the sum of the numbers I told you from 5,050 is exactly the number I omitted from the series! In this case, you were able to answer an important question related to the data you received, without having to remember those data.
The questions I study relate to very large collections of numbers—even trillions of them (one trillion is a million millions, or 1,000,000,000,000). Such large collections of numbers cannot be stored in a computers’ memory, so we must find out what we can know about them without saving them. For example, if we want to know whether there is a number that appears twice in the collection, we cannot know this without remembering all the numbers. But if we want to know approximately how many distinct numbers are in the collection, there is a way we can do it without remembering the numbers (Figure 4) [3]. I will not elaborate on how to do so, since it is a bit complicated, but I will mention that we can estimate it in a way that gives us a result that is very likely to be very close to the actual result. For example, it is possible that, with a probability of 99% (meaning 99 cases of out 100) we will get a result that is <1% incorrect compared to the real result; and with 1% probability (meaning 1 case out of 100) we will get a result that is not close to the real result. As you see, the mathematics I study allows us to get to surprising and unpredictable results, and that is part of its beauty—it allows us to expand our ideas beyond what we originally thought to be true.

- Figure 4 - Algorithms for dealing with data streams.
- There are situations in which we must deal with immense amounts of data, and we are not capable of saving it all in a computer—like constantly streaming data on the internet (illustrated here as the flow of many balls). To conclude something important about these data without saving them, we must use different mathematical “tricks” (bottom right) that allow us, with high probability, to get a result that is close to the actual result that we are unable to compute accurately without saving the data.
These studies laid the foundation for an organized mathematical analysis of large data streams (called big data) using limited computer memory. This way, users can extract their desired data with very high accuracy, without having to save all the numbers. These studies also have important implications for several other areas of mathematics, including information theory and graph theory.
Recommendations for Young Minds
A Mathematician’s Life
For people who are not mathematicians, it is hard to imagine what the life of a mathematician looks like. Even as an undergraduate in mathematics, the meaning of conducting mathematical research was not clear to me. As a mathematician at a university, I must fulfill all sorts of demands and requirements: teach courses, mentor students, and publish papers. Sometimes I must write letters of recommendation for my colleagues, or review articles written by other mathematicians dealing with areas that fall within my expertise. When I arrive at the office in the morning, I open my computer and read emails. Often, people write to me with mathematical questions and ask if I can help or direct them to relevant resources. Sometimes the questions I receive are related to something I already know, or to something very similar to what I know—then I know how to answer them. Other times, I get questions about something I do not know but am interested in thinking about, and then I ponder the question for a while to see if any solutions come up.
At other times during the day, I think about mathematical problems related to my personal research. Sometimes I read articles that other people published on mathematical questions that I am interested in, and sometimes I sit and think about how to solve a certain open problem. In contrast to what non-mathematicians might think, direct work with equations and computations is not a big part of solving mathematical problems. The common image of a mathematician as someone who does long computations and eventually gets a result is not accurate. Most of the time, I am occupied with finding potential ways of solving a problem, and I ask myself questions like, “what sort of computation should be performed here?” or “what can advance my understanding of this problem?” Sometimes, at the end of the process, there will be an equation that I will need to solve or a calculation that I must perform, but that is only a small part of the process—it is often the product of an idea that occurred to me first.
It is important to note that researchers—both mathematical and otherwise—often experience frustration from failing to solve the problems we are trying to solve. If we succeed at solving our problems too frequently, that means our problems are too simple and not interesting enough! This ongoing lack of success, which is a substantial part of good research, is often accompanied by nagging thoughts such as “this was probably the last time I could solve something… from now on I will not succeed.” My experience proves that this thinking is not true, and part of the confidence you build along the way comes from learning how to avoid believing these self-doubting thoughts. Part of my willingness to deal with the struggles of mathematical research comes from the hope that I will successfully understand something I did not understand before, or solve a problem that has never been solved. I learned to enjoy the challenges in this process—the moments I do not enjoy are important because they make the enjoyment more meaningful and satisfying when it happens. Also, when I feel “stuck” in my work, I make sure to do something to change my internal state, so that I am more likely to have new and different ideas. Sometimes I will choose to think about another mathematical problem, and sometimes I will do something else entirely—read a book, watch a movie, or play a sport. Occasionally, a new idea will be generated from something I hear or read. Most times, I do not know what sparked my new ideas. Although I do not know how to track the sources of my ideas, my experience has taught me that changing what I am doing frequently supports the appearance of new ideas.
On Young Mathematicians
It might interest you to know that young researchers have a certain advantage over experienced researchers, because they are less hesitant about investigating hard problems that many people have failed to solve. As an experienced researcher, I know of a variety of unsolved mathematical problems, and I know how to estimate their level of difficulty. On one hand, a beginning student might not know the history of a certain mathematical problem and not know how to estimate how difficult it is. Sometimes this lack of knowledge might serve them, and they eventually succeed at solving an important, previously unsolved problem. On the other hand, it is important to emphasize—especially to those of you who find school mathematics extremely easy—that you cannot do and know everything yourself. Even if you are very skilled and intelligent, you will still need to learn a lot of the knowledge accumulated by whole generations of smart mathematicians who spent much of their time developing mathematical methods. New students can acquire this knowledge by studying scientific literature, listening to lectures, and having discussions with other mathematicians interested in the same areas.
Thoughts About Prizes and Achievements
I have received quite a few prizes over the course of my career. Each time, I was happy to have my work recognized, and each prize proved to me that what I do interests other people as well. The prizes I received positively impacted my career and allowed me flexibility in my academic choices. Although I enjoy receiving prizes, I must emphasize that they are not the aim of my research. Prizes are not guaranteed—they are dependent on factors that I cannot control. In many cases, I can only recognize in retrospect the importance of the things I have worked on. My research on the properties of data streams is a good example—it turned out to be important later on, and it opened a new area of mathematics called streaming algorithms. My first aim in my research is to do what most interests me. This relates to my general recommendation: do what you love, and love what you do. These are two sides of the same coin, and both are important. Instead of doing something that does not interest you very much, thinking that it will eventually lead you to success, choose to do what you love to do. Sometimes it will lead to success and sometimes it will not, but at least you will spend your life engaged in work that is meaningful for you.
Glossary
Objective: ↑ Not influenced by personal opinion and unable to be argued about.
Sociologist: ↑ A person who studies society, including both the groups and individuals that make it up and society as a whole.
Combinatorics: ↑ An area of mathematics that studies the properties of finite groups of objects.
Topology: ↑ A branch of mathematics dealing with conserved properties of space.
Algorithmic Game Theory: ↑ A combination of game theory, which studies interactions between factors with different interests, and computational theory, which deals with models of computation and algorithms for performing computations.
Information Theory: ↑ A branch of mathematics that studies the transfer of information between a source and a target.
Graph Theory: ↑ An area of mathematics dealing with graphs—combinatorial structures appearing in many contexts.
Acknowledgments
I wish to thank Or Raphael for conducting the interview which served as the basis for this paper and for co-authoring the paper and Alex Bernstein for providing the figures.
Conflict of Interest
The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
[1] ↑ Van Lint, J. H., and Wilson, R. M. 2001. A Course in Combinatorics. Cambridge: Cambridge University Press.
[2] ↑ Alon, N. 1987. Splitting necklaces. Adv. Math. 63, 247–53.
[3] ↑ Alon, N., Matias, Y., and Szegedy, M. 1999. The space complexity of approximating the frequency moments. J. Comput. Syst. Sci. 58:137–47.
