Abstract
Noise pollution can reduce the quality and even the length of our lives, causing around 12,000 early deaths in Europe each year. Devices called resonators can be used to reduce unwanted noise from engines and fans, by cancelling out sound waves. However, the sound waves of low-pitched noises are difficult to cancel because they are very big: sometimes as long as 17 m! To cancel such large sound waves would require an impractically large resonator. One solution to this problem is to make the resonator from a special class of material called a metamaterial. Metamaterials have specially designed structures that give them properties that are not found in ordinary materials. This article explains how we used mathematics to design a metamaterial that slows down sound waves. Slowing the sound allows us to use smaller resonators, so we can cancel lower-pitched noises than we can with ordinary materials.
Have you ever tried to do your homework or read a book while somebody nearby is mowing a lawn or using a hairdryer? The noise can make it difficult to concentrate! Now imagine living close to a busy airport. The European Environment Agency estimates that aircraft noise has harmed the learning of 12,500 European schoolchildren [1]. Unwanted noise can damage our health, too, leading to around 12,000 early deaths in Europe each year, due to an increase in stress-related heart disease.
One way to reduce noise from engines and fans is to include noise cancellation in their design, but noise-cancelling devices can be bulky and impractical. In this article, we describe how we use mathematics to tackle this problem, by designing a material that we can use to make smaller noise-cancelling devices. First, we will look at sound waves and what happens when they combine. Next we will describe how a simple noise-cancelling device works, and why the size of the device matters. Then we will show how our new material, designed using mathematics, lets us shrink the size of a noise-cancelling device.
The Characteristics of Sound Waves
Sounds are caused by vibrations. When an object vibrates, the air around the object vibrates too. The vibrating air molecules make other air molecules around them vibrate and so on, all the way to our ears. Inside our ears, tiny bones vibrate, and our brains understand this as sound. In a sound wave, it is the vibrational movement that travels along, and not the air particles.
Air particles in a sound wave are squashed together and stretched apart like the coils in a slinky being stretched and released. Although the particles move back and forth along the direction the wave is traveling, we often draw sound waves as wavy lines going up and down, more like ocean waves (Figure 1A). The height of the line tells us the pressure—how squashed together the particles are at any point. The highest points (peaks) show where the particles are most compressed, and the lowest points (troughs) where they are the most separated.
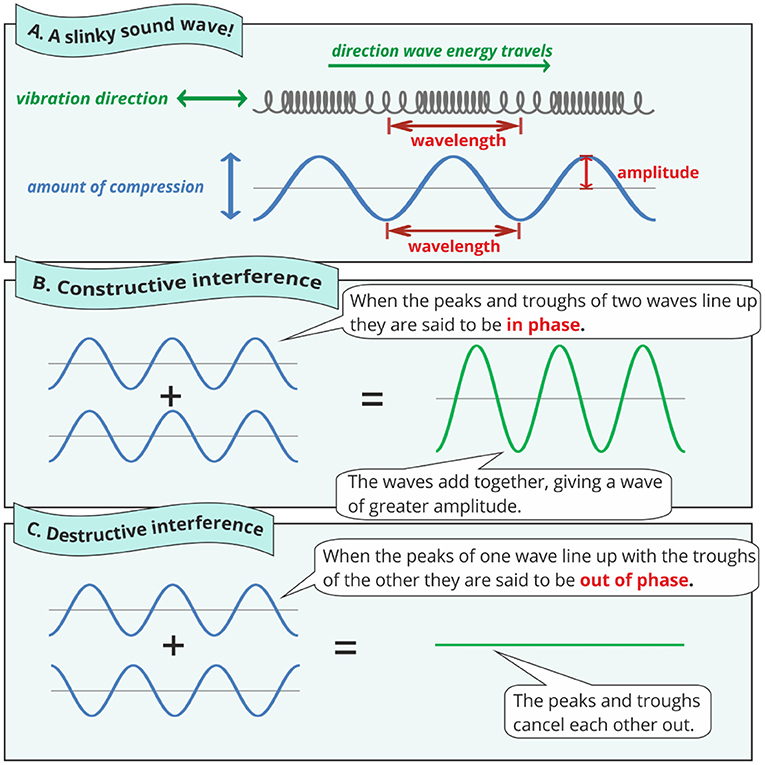
- Figure 1 - (A) Sound waves are characterised by their wavelength and amplitude.
- The larger the amplitude, the louder the sound. (B) Constructive interference produces a wave of greater amplitude, making the sound louder. (C) In destructive interference, waves cancel each other out, making sound quieter.
In our wave drawing, the distance from the highest or lowest point to the center is called the amplitude. Amplitude is a way of measuring loudness. It tells us how close together or spaced out the particles are, compared to their resting positions. The bigger the difference, the louder the sound. We measure loudness in units called decibels (dB).
As well as the amplitude, we also measure the wavelength and frequency of a sound. The wavelength is the distance from a point on one wave to the same point on the next; for example, the distance from the peak of one wave to the peak of the next. The frequency is the number of waves that pass a fixed point in 1 s . It is measured in hertz (Hz), or waves per second. Remember the slinky: if you stretch and release the slinky rapidly, you will create a high-frequency wave. Reducing the number of movements per second lowers the frequency. Frequency tells us about the pitch of a sound—the higher the frequency, the higher-pitched the sound.
How Can Adding Sounds Together Result in Less Sound?
When waves meet, they affect each other in different ways. We call this interference. The type of interference depends on how the waves line up. Figure 1B shows two waves, positioned so that their peaks line up exactly. We say the waves are in phase. Waves that are in phase add together to give a wave with higher peaks and a bigger amplitude. For sound waves, this gives a louder sound. We call this constructive interference.
Now look at Figure 1C. Here, the peaks of one wave line up with the troughs of the other. We call this being out of phase. The result is that the two waves cancel each other out and you end up with no wave at all! We call this destructive interference. For sound waves, destructive interference results in a quieter sound.
Noise Cancellation: The Quarter-Wavelength Resonator
Many gadgets rely on destructive interference to reduce unwanted noise. For example, noise-cancelling headphones play sound waves that are out of phase with the unwanted sounds. When the waves meet, they cancel. Other devices rely on their geometry to do the work. These include the quarter-wavelength resonator (QWR), which can be used to reduce noise made by engines and fans [2, 3].
The exhaust pipe on a vehicle takes fumes away from the engine and releases them into the air. But noise also travels along the pipe! A QWR is an extra bit of pipe that branches off the main exhaust. It traps and reflects sound waves. Figure 2 shows how it works. Sound travels down the pipe, some of it enters the side branch, is reflected, and meets up again with the original sound wave. The reflected and original waves are out of phase when they recombine, so destructive interference happens, making the sound quieter.
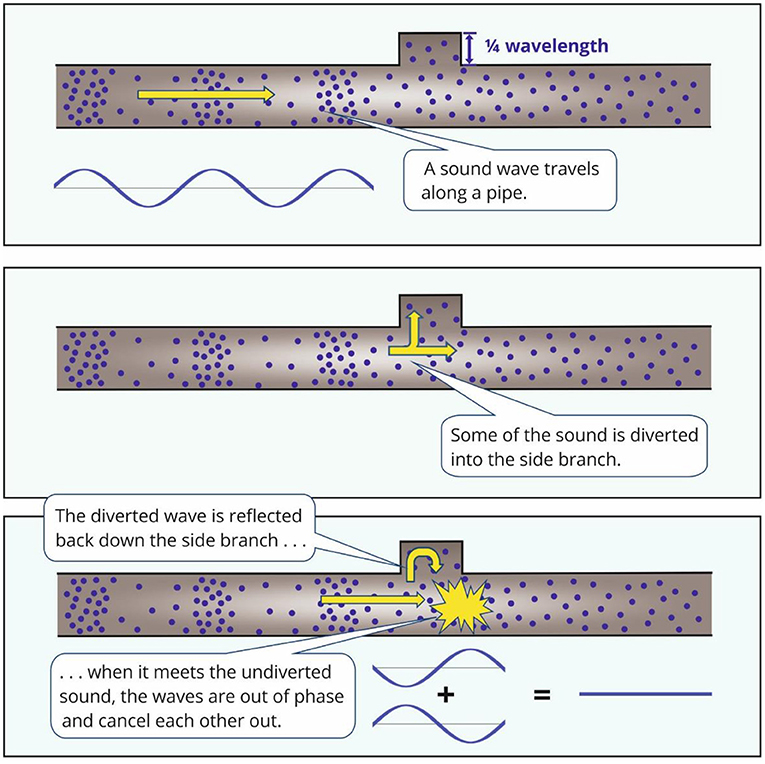
- Figure 2 - The quarter-wavelength resonator can make sounds quieter by diverting some of the sound.
- The diverted and undiverted sound waves recombine with destructive interference, quieting the sound that exits the pipe.
The length of the side branch is important: for the two waves to be out of phase when they meet, its length must be one quarter of the wavelength of the sound we want to cancel. This is why we call it a quarter-wavelength resonator.
The Problem of Low-Frequency Noise
So far so good. But what if the sound waves are very long? The side branch must be one quarter as long as the sound wave, so the bigger the wavelength, the bigger our QWR needs to be. And sound waves can be very large! Low frequency sounds have the longest wavelengths, and high frequency the shortest. Humans can hear frequencies as low as 20 Hz, which corresponds to a 17-m-long wave!
The noise from engines can include frequencies with wavelengths longer than 3 m [4]. A QWR would need to be 75 cm long to eliminate a 3 m long sound wave by destructive interference. Large devices add weight and cost, not to mention being difficult to fit!
Designing Materials With Maths
We used mathematical modelling to design special materials to help solve this problem. Our materials are called metamaterials. The properties of metamaterials depend on their shape and structure, rather than the stuff they are made of. Metamaterials interact with waves in ways not seen in ordinary materials [5]. We used a 3D printer to make QWRs with metamaterial structures inside them (Figures 3B,C). Both are 4 cm long with thin, oval shapes stacked inside. One has a very narrow gap at each side, while the other has a slightly wider gap in the centre. We also made a normal QWR without a metamaterial structure inside (Figure 3A).
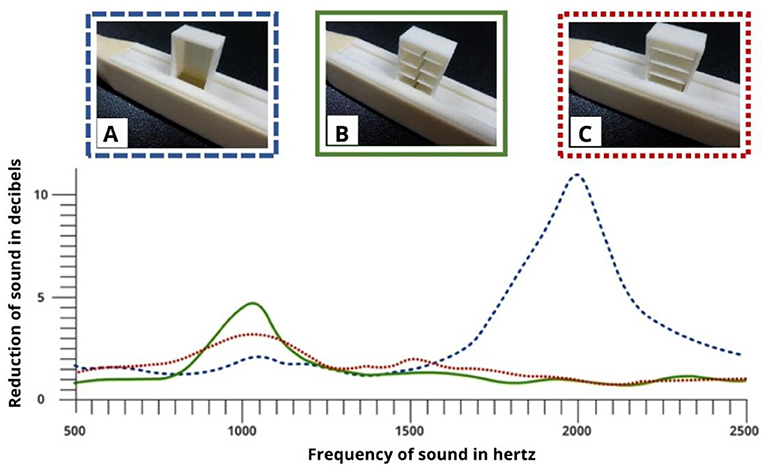
- Figure 3 - Comparing metamaterial QWRs (B,C) with “normal” QWR (A).
- (A) The normal QWR (blue) has a peak at 2,000 Hz, reducing sound at that frequency by about 10 dB. (B) This QWR (green) shows a 5 dB sound reduction peak at 1,000 Hz. (C) This QWR (red) also reduces sound at 1,000 Hz, but less effectively. The decibel scale is not linear: a reduction of 3 dB reduces the sound energy by half and 10 dB is a 10-fold reduction. The reductions measured in dB are the same however loud the initial sound is.
Our metamaterials slow down sound to about half its normal speed. They do this by stretching out the space through which the sound wave travels. Slowing down the sound has an effect you might not expect: it makes the metamaterial resonators cancel sound at lower frequency than the normal QWR does. This is because of the mathematical relationship between wavelength, frequency, and the speed of sound:
For a QWR we can rearrange this equation so that:
Where the wavelength is four times the length of the QWR. In this equation if we halve the speed of sound, the frequency of sound reduced will be halved. So we expect our metamaterial resonators to cancel sound at half the frequency compared to a normal QWR.
Our Results
Figure 3 shows what happened when we tested the three QWRs. We measured how much loudness was lost at a range of frequencies. We expected the metamaterial QWRs to reduce sound at half the frequency compared to the normal resonator, and indeed, both metamaterial QWRs did so! The metamaterial in Figure 3B has the wider gap in its centre rather than two narrower gaps at the edges, and this small difference makes it more effective than the metamaterial in Figure 3C; it reduces sound by 5 decibels. This is a significant difference, similar to the drop in loudness you would get by increasing your distance from the source of a sound by 1.8 times (for example, if you are 100 m away, it would be like moving to 180 m away).
Why Does Halving the Frequency Mean Smaller Devices?
We know that the lower the frequency of a sound wave, the longer its wavelength. If we halve the frequency of a sound in the air, we double its wavelength. QWRs normally eliminate sounds with wavelengths four times their length, but our metamaterial QWRs eliminate sounds with wavelengths eight times their length. Instead of quarter-wavelength resonators, we could call them eighth-wavelength resonators! So, with a metamaterial, we can halve the length of the noise-cancelling device needed for a given frequency. This could save space and resources and allow us to reduce nuisance noise at lower frequencies than possible with everyday materials. Our research is a step toward a quieter future!
Glossary
Amplitude: ↑ The maximum distance of a particle in a wave from its resting position. Sound waves with large amplitudes are loud and low amplitude sound waves are quiet.
Wavelength: ↑ The length of one wave, measured in metres from a point on one wave to the same point on the next wave.
Frequency: ↑ The number of waves that pass a fixed point in 1 s , or the number of oscillations per second. Measured in Hertz (Hz, or S−1).
Constructive Interference: ↑ When waves add together so that their peaks and troughs line up, the result is a higher amplitude wave.
Destructive Interference: ↑ When waves add together so that the peaks of one line up with the troughs of another and the peaks and troughs cancel each other out.
Quarter-Wavelength Resonator: ↑ A noise-cancelling device that operates via destructive interference.
Metamaterial: ↑ A special material with unusual properties that are normally determined by its geometrical structure.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Original Source Article
↑Rowley, W. D., Parnell, W. J., Abrahams, I. D., Voisey, S. R., Lamb, J., and Etaix, N. 2018. Deepening subwavelength acoustic resonance via metamaterials with universal broadband elliptical microstructure. Appl Phys Lett. 112:251902. doi: 10.1063/1.5022197
References
[1] ↑ European Environment Agency. 2020. Environmental Noise in Europe 2020. EEA. Report No: 22/2019. doi: 10.2800/686249
[2] ↑ Wu, C., Chen, L., Ni, J., and Xu, J. 2016. Modeling and experimental verification of a new muffler based on the theory of quarter-wavelength tube and the Helmholtz muffler. SpringerPlus 5:1366. doi: 10.1186/s40064-016-3060-1
[3] ↑ Field, C. D., and Fricke, F. R. 1998. Theory and applications of quarter-wave resonators: a prelude to their use for attenuating noise entering buildings through ventilation openings. Appl Acoustics. 53:117–32. doi: 10.1016/S0003-682X(97)00035-2
[4] ↑ Ih, J. G., Choi, C. Y., Kim, T. K., Jhang, S. H., and Kim, H. J. 2011. Optimal design of the exhaust system layout to suppress the discharge noise from an idling engine. Int. J Automot. Technol. 12:617–30 doi: 10.1007/s12239-011-0072-2
[5] ↑ Cummer, S. A., Christensen, J., and Alù, A. 2016. Controlling sound with acoustic metamaterials. Nat Rev Mater. 1:16001. doi: 10.1038/natrevmats.2016.1
