Abstract
Human behavior is a diverse, complex, and highly interesting phenomenon. Despite the many differences that exist between any two people, we can find patterns that characterize typical behaviors in various situations, such as in a classroom or at a family dinner. The research field called behavioral economics studies human behavior in financial situations. In this article, I will present the main findings of the prospect theory, which I developed together with the late Amos Tversky. Prospect theory explains human choices in situations that involve gambling, and it answers questions such as whether people consider gains and losses equally and how a person’s initial financial situation influences the value they give to gains and losses. At the end of the article, I will share important insights from my scientific career and explain why happiness has two faces.
Professor Daniel Kahneman won the Nobel Prize in Economic Sciences in 2002 for having integrated insights from psychological research into economic science, especially concerning human judgment and decision-making under uncertainty.
Prospect Theory
Imagine that one of your friends suggests playing the following game: she will toss a coin and you need to guess whether it will land heads up or tails up. If the coin lands heads up you gain $3, and if it lands tails up you lose $3. In this situation, the amount you would gain or lose is the same, and there is a 50% chance of each happening, because the chances of heads and tails are equal. Would you choose to play this game? What if your friend changed the rules so that you would get $5 if the coin lands heads up but lose $3 if it lands tails up? In this situation the gain and loss are different, but there is still a 50% probability for each case (Figure 1).

- Figure 1 - Coin toss with gains and losses.
- (A) A gamble with equal (50%) chance for a gain or a loss. Would you play this game if you would gain $3 (USD) if the coin lands on the elephant’s head up and lose $3 if it lands elephant’s tails up? (B) A gamble with a 50% chance for a gain or a loss, but with different gain and loss amounts. In this version, you would receive $5 if the coin lands heads up and lose $3. if it lands tails up. Would you choose to play this game?
Now imagine another situation where your friend suggests playing a different game: she will roll an ordinary six-sided dice. If she rolls any number from one to four, you will receive $3. But, if she rolls a five or a six, you will lose $3. In this situation, an equal amount would be gained or lost, but there are different probabilities: a 66% chance of winning (4 out of 6) and a 33% chance of losing (2 out of 6). Would you play this game (Figure 2)?
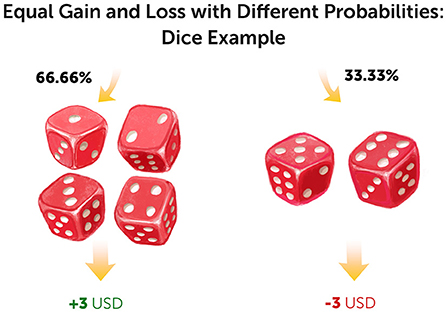
- Figure 2 - Dice throwing with equal gain and loss but different probabilities.
- In this game, if you roll a dice and get any number from one to four, you win $3 (USD, left side), but if you roll a five or a six, you lose $3 (right side). Would you want to play this game?
These are examples of simple gambling games with different situations of gain vs. loss. Now think about situations where there are only gains of various sizes—for example, if someone asks you to choose between getting a guaranteed $3 or having an 80% chance of receiving $6. Which option would you choose now? Or, if you were offered $3 now or $10 if you wait 2 weeks, which would you choose?
The prospect theory that I developed with my late friend, Amos Tversky, deals with the situations described above. Prospect theory is a theory of behavioral economics, which studies the choices that people make in uncertain situations, like when they are gambling [1–3]. Prospect theory aims to explain why and how people make their choices. In the next part of the article I will present two central findings of prospect theory, and explain their implications and how they are related to the situations you have seen above.
What do People Think of When they Gamble?
In the past, it was believed that when people think about the financial implications of gambling, they evaluate what their financial status will be if they win or if they lose. For example, a merchant that sends his goods (perfumes, for example) in a ship from Amsterdam to Saint Petersburg knows that there is a 5% probability that the ship will sink along its route and will not reach its destination. The merchant therefore thinks about two options. In the first, there is 95% probability that the ship will arrive safely to its destination. If this happens, he could sell the perfumes and make a predictable profit.
In the second option, there is a 5% probability that that the ship will sink, and the merchant will lose the money he spent on the perfumes. The merchant needs to decide whether to purchase insurance for the contents of the ship. Should he decide to invest an amount of money that will cover the cost of the perfumes if the ship sinks, or should he take the risk and not pay the insurance, hoping that the ship will arrive safely?
The famous scientist Daniel Bernoulli (1700–1782) studied this problem. Bernoulli theorized that people think about the future state of their assets. Namely, when people make an economic decision (gamble), they estimate what their financial situation will be if they win the bet, and what their financial situation will be if they lose. At this point, Amos Tversky and I entered the picture. We noticed that, when it comes to gambles that people make in everyday life (which usually do not involve gambling on a big merchandise that could get lost on the way as in the case of the ship described above), people think about gains and losses and not about the overall financial state they will be in after the gamble [2–4]. Recall the games we described above: when you choose whether to take the gamble, you probably thought about how much money you would gain if you won and how much money you would spend if you lost. Chances are you did not think about the overall amount of money you would have in your private cash box in each of these cases. In other words, people focus on changes in their financial state resulting from the gamble. This insight is usually presented using a curve called the value function (Figure 3) [2]. These changes are measured relative to the person’s financial status before the bet, which we call the “zero state,” portrayed by the 0 at the origin of the axes in Figure 3.
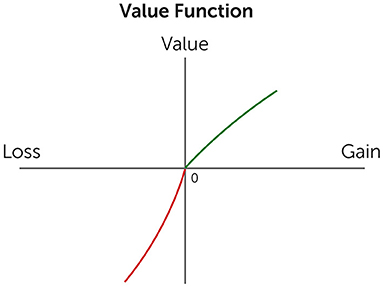
- Figure 3 - The value function.
- A major innovation of prospect theory is the shift from the emphasis on the final financial situation of the gambler, after the realization of the bet, to the emphasis on the gains (Gains) and losses (Losses) with respect to the initial financial status of the gambler before the bet, represented here by the origin of the axes (“0”). The gain or loss is measured relative to it, and is associated with a subjective value (Value) of the person making the bet. Each person decides for themselves how important profit (gain) is to them and how much loss “hurts” them. Prospect theory says that losses hurt more than does an equivalent amount of gain (the red curve is steeper than the green curve) (Adapted from [2]).
Loss Aversion
Now that we understand that it is the changes in a gambler’s financial state that carry value, we can ask whether gains and losses have the same “weight” or importance to the gambler. Let us go back to the game in Figure 1. The first version of the game, in which there are equal chances for gain and loss and the gain and loss are equal, is a type of gamble that people do not like to take. People much prefer the gamble offered in the second version, in which the value of the gain is higher than the value of the loss and the chances for gain and loss are equal. In other words, people need the “compensation” of a potentially greater gain to allow for the risk of losing. The important conclusion is that people’s attitudes toward gains and losses are not equal. People are averse to loss (meaning they dislike it) more than they are attracted to gain. We called this loss aversion [5].
Loss aversion is graphically displayed in Figure 3. Look at the green curve on the right side of the graph, representing the value people attribute to gains, and compare it to the red curve on the left, representing the value people attribute to losses. You can see that the gain curve rises more slowly, it is more moderate, than the loss curve, which is steeper. This means that, for the same actual value of gain and loss (like +$3 and –$3), people will experience the loss as more negative than they will experience the gain as positive. Test this on yourself: would you be more excited from gaining $3 than you would be upset by losing $3? Most of you will say that it is more upsetting to lose $3 than it is exciting to gain $3. This human characteristic shows up in many cultures, and we believe it has an evolutionary basis (Challenge: could you think how this characteristic of increased aversion to loss serves humans from an evolutionary perspective?). It is interesting to note that, although awareness of loss aversion increased following our studies, loss aversion itself did not decrease. But our studies enabled us to understand people’s behavior in financial situations, which earlier theories had failed to explain.
Recommendation for Young Minds—The Two Faces of Happiness
Finally, I would like to share with you some important insights from my research career that are not directly related to the world of economics. The first insight comes from behavioral psychology and arises from the question: “what makes people happy?” The other insight emerged from my own observations of myself as a scientist.
Happiness is a meaningful and elusive quality in every person’s life. The road to happiness is highly individual and it depends on many factors. Nonetheless, you should be aware that there are two types of happiness—being happy in your life, and being happy about your life1 (Figure 4) [6, 7]. Being happy in your life, also called experienced happiness, relates to the momentary experience in life: Is it pleasant to be myself? Do I feel good at the moment? This type of happiness is closely related to our moods. It turns out that, on average, people are the happiest when they spend time with people they love and who love them. In contrast, being happy about your life, also called life satisfaction, relates to general satisfaction from life: Is my life successful? Am I proud of my achievements? In other words, satisfaction results from looking back at your life and weighing it in terms of success and failure2.

- Figure 4 - The two faces of happiness.
- Overall happiness is made up of two types of happiness—being happy in your life (experienced happiness) and being happy about your life (life satisfaction). (A) Being happy in your life relates to momentary enjoyment, which is usually caused by spending time with people you love. (B) Being happy about your life, i.e., satisfaction, is related to looking back at your life and feeling that your goals were accomplished. Wisdom lies in finding the way to fulfill both types of happiness, which does not always happen at the same time [6].
My recommendation, therefore, is that you should think about two different aspects of happiness: how you would like to spend your time (being happy in life), and what your life goals are (being happy about life). These two aspects do not always go hand-in-hand at any specific moment. But if you pay attention to both, your chances of experiencing both increases. Another important thing for you to know is that, in additional studies, we found that the relationship between financial wealth and happiness is not as simple and clear as people tend to think [8]. So, to be happy, my recommendation is not to focus your attention too much on financial wealth. Instead, participate in various enjoyable activities throughout your life and choose a variety of goals—not only financial ones.
The Scientist is Like a Kid who Likes to Change Her Mind
To me, being a scientist is kind of like deciding to remain a child and maintaining a high level of curiosity. Of course, scientists do not fully understand the world around them, but they do make great efforts to try to understand it. As a scientist, I also like to change my mind. There are scientists who find it hard to change their opinions—they cling on to it and do not let go. For me, it is the opposite—only when I change my mind do I feel that I really learned something new. In this sense, working in science is an ongoing cycle. Again and again, there are moments of, “oh, how could I have been such a fool and not seen this earlier?” This experience of seeing things anew repeats over and over during life of a scientist. It continues throughout your life if you decide to become a scientist. It still happens to me at the age of 88 (my current age).
Glossary
Prospect Theory: ↑ A theory dealing with human behavior in situations of financial gambles. This theory is part of a branch in economics called behavioral economics.
Behavioral Economics: ↑ A branch of economics that explores the factors influencing people’s choices in financial situations.
Value Function: ↑ A function describing the connection between the subjective value that people attribute to gain or loss, and the objective value of the gain and loss.
Loss Aversion: ↑ A greater dislike of losses compared to the attraction of comparable gains. For example, people tend to avoid gambles in which the amount and probability of loss are equal to the amount and probability of gain.
Conflict of Interest
The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
I wish to thank Noa Segev for conducting the interview which served as the basis for this paper, and for co-authoring the paper. Thanks to Alex Bernstein for the figures.
Footnotes
1. ↑For more information, see: Daniel Kahneman: Moving to California Will Not Make You Happy.
2. ↑For more information, see: The riddle of experience vs. memory | Daniel Kahneman.
References
[1] ↑ Tversky, A., and Kahneman, D. 1974. Judgment under uncertainty: heuristics and biases: biases in judgments reveal some heuristics of thinking under uncertainty. Science 185:1124–31. doi: 10.1126/science.185.4157.1124
[2] ↑ Kahneman, D., and Tversky, A. 1979. Prospect theory: an analysis of decision under risk. Econometrica 47:363–91. doi: 10.2307/1914185
[3] ↑ Kahneman, D., and Tversky, A. 2013. “Prospect theory: an analysis of decision under risk,” in Handbook of the Fundamentals of Financial Decision Making: Part I, eds L. C. MacLean and W. T. Ziemba (World Scientific Press). p. 99–127. doi: 10.1142/9789814417358_0006
[4] ↑ Kahneman, D., and Tversky, A. 2013. “Choices, values, and frames,” in Handbook of the Fundamentals of Financial Decision Making: Part I, eds L. C. McLean and W. T. Ziemba (World Scientific Press). p. 269–78. doi: 10.1142/9789814417358_0016
[5] ↑ Tversky, A., and Kahneman, D. 1991. Loss aversion in riskless choice: a reference-dependent model. Quart. J. Econ. 106:1039–61. doi: 10.2307/2937956
[6] ↑ Kahneman, D., and Riis, J. 2005. Living, and thinking about it: two perspectives on life. Sci. Wellbeing 1:285–304. doi: 10.1093/acprof:oso/9780198567523.003.0011
[7] ↑ Kahneman, D., Schkade, D. A., Fischler, C., Krueger, A. B., and Krilla, A. 2010. “The structure of well-being in two cities: Life satisfaction and experienced happiness in Columbus, Ohio; and Rennes, France,” in International Differences in Well-Being, eds E. Diener, J. F. Helliwell, and D. Kahneman (Oxford University Press). p. 16–33. doi: 10.1093/acprof:oso/9780199732739.003.0002
[8] ↑ Kahneman, D., Krueger, A. B., Schkade, D., Schwarz, N., and Stone, A. A. 2006. Would you be happier if you were richer? A focusing illusion. Science 312:1908–10. doi: 10.1126/science.1129688
