Abstract
Traveling to different destinations is a major part of our lives. We visit a variety of locations both during our daily lives and when we are on vacation. How can we find the best way to navigate from one place to another? Perhaps we can test all of the different ways of traveling between two places, but another method is to use mathematics and computation to find a shortest path between them. In this article, we discuss how to construct shortest paths and introduce Dijkstra’s algorithm to minimize the total cost of a path, where the cost may be the travel distance, the travel time, or some other quantity. We also discuss how to use shortest paths in the real world to save time and increase traveling efficiency.
What Is a Path?
Every day, we make decisions about which routes we use to travel between different places. In your home, you may travel from your bedroom to your kitchen. Outside your home, you may travel from your home to school. Suppose that we have a network of places that are connected to each other by streets and walkways. Each of these locations is called a node, and the streets and walkways are called edges. The “neighbors” of a node are the nodes to which it is connected by an edge. A path is a sequence of edges between an origin node and a destination node [1, 2].
Shortest Paths
In mathematics, people study the lengths of paths to construct short paths. It is often useful to find a shortest path. A shortest path is a path between two nodes that has the fewest edges if the cost of traveling along each edge is the same (for example, if each edge is a street of the same length). More generally, given an origin node and a destination node, a shortest path from the origin node to the destination node is a path that has the lowest total cost among all paths from the origin to the destination [1]. To calculate the cost of a path, one sums the individual costs of all of its edges. A cost can measure distance, time, or something else. For example, in the small city map in Figure 1, a shortest path from home to school may be one that takes the least amount of time among the possible paths. There can be more than one shortest path between two nodes in a network because multiple paths can have the same minimum cost. That is why we refer to “a” shortest path between two nodes (even though it sounds weird) rather than “the” shortest path between them.
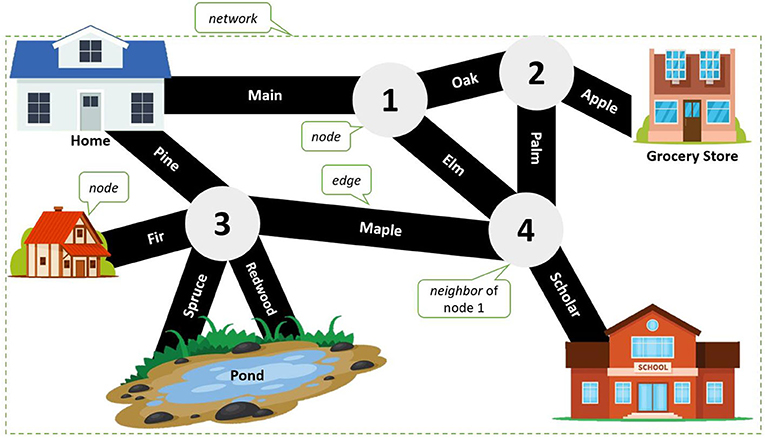
- Figure 1 - In this small city map, which is an example of a network, locations (i.e., nodes) 1–4 occur at the intersections between streets (i.e., edges).
- Each of the locations (the blue and red houses, the pond, the school, and the grocery store) is also a node. Activity 1: Trace a path from the blue house to the school on the map. Which streets (i.e., edges) do you take in the picture? Which streets do you take when you travel from your home to school in real life? (This figure is inspired by the figure at http://clipart-library.com/clipart/449476.htm. Our figure also uses public clip art.)
You probably already think about shortest paths in your daily life when you are going to different places. In our bedroom-to-kitchen example, it would not make much sense to walk from your bedroom, then to the laundry room, then outside to your backyard, and finally to your kitchen if you only want to travel from your bedroom to your kitchen. It would be much faster to walk directly from your bedroom to your kitchen without stopping in the laundry room and your backyard first. In a trip with locations that are close to each other, there are only a few street intersections (i.e., nodes) and you may be able to try out most of the different paths to find a shortest path. But if the locations are farther apart—for example, your home, your school, and a toy store in a different city—then finding a shortest path is much more difficult. How do navigation tools like Google Maps determine the best way to reach a destination? One way is to solve the shortest-path problem, which is the mathematical problem of finding a path between two nodes in a way that minimizes the sum of the costs of the edges in the path1.
In mathematics, we often label nodes using numbers (see the intersections in Figure 1) or letters (see Figure 2). For simplicity, we also suppose that everything is two-dimensional (as in a drawing on a piece of paper), so we will measure distance in the way that we would measure it between two spots on the floor in your home. We will not worry about things like height or the curvature of the Earth. In the network in Figure 2, if we want to find a shortest path from node A to node F, we should choose the edges with the lowest costs. For example, instead of choosing the edge with cost 4 from node A to node B, we choose the edge with cost 2 from node A to node C. Choosing the edges with the lowest costs to find a shortest path is one of the key ideas in Dijkstra’s algorithm2,3.
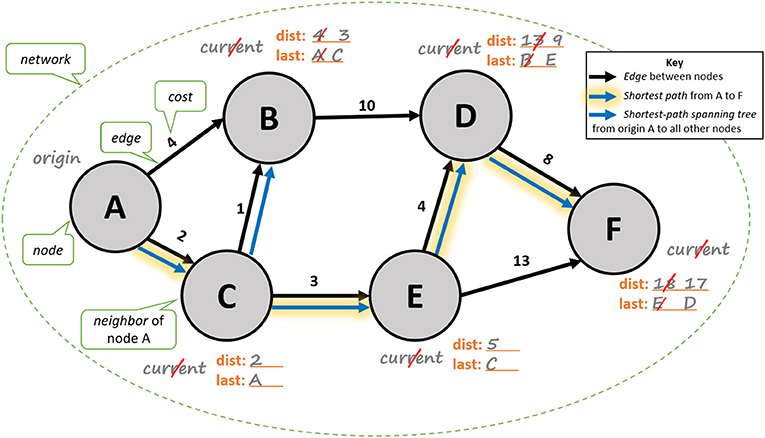
- Figure 2 - In this network, following the highlighted blue arrows shows us the shortest path from node A to node F.
- The numbers indicate the costs of the edges (which are not drawn to scale). The blue arrows show the shortest-path spanning tree that has A as the origin node. Observe that the shortest path from node A to node F is part of the shortest-path spanning tree. The label “dist” indicates the total distance from the “origin” node to a particular node, and the label “last” indicates the last node that one passes through to reach a particular destination node from the “origin” A. In the section called “Dijkstra’s Algorithm,” we give a detailed explanation of the steps to determine a shortest path. [This figure is inspired by figures that are available online1,3.]
Dijkstra’s Algorithm
An “algorithm” is a precise set of steps to follow to solve a problem, such as the shortest-path problem [1]. Dijkstra’s algorithm is a famous shortest-path algorithm; it is named after its inventor Edsger Dijkstra, who was a well-known Dutch computer scientist4. One can use Dijkstra’s algorithm to create a shortest-path spanning tree (see Figure 2) to find a shortest path from an origin node to each other node in a network by separately calculating the distance from the origin to each of the other nodes. In this discussion, we are using distance as our cost, but one can use Dijkstra’s algorithm for any type of cost.
In Figure 2, we show how to use Dijkstra’s algorithm to construct a shortest-path spanning tree for a connected network. Follow along in Figure 2 as you read our explanation, and watch Video 1 for an animation of this example.
Here are the steps that we take:
1. We shade in the “origin” node. (See node A in Figure 2.) For each of the origin node’s neighbors, we set the initial value of “dist” to be the distance from the origin node to that neighbor and the initial value of “last” to be the origin node. In the example in Figure 2, by the end of this step, we fill in values for “dist” and “last” for nodes B and C. The “dist” and “last” entries for nodes D, E, and F are still blank.
2. We identify the unshaded node with the lowest “dist” value (excluding blanks) and label this as our “current” node. For example, if we begin with node A as the origin, then the current node is node C because the “dist” from A to C is less than the “dist” from A to B. If there is a tie, we choose any of the nodes with the smallest “dist” value.
3. We do the following steps for each unshaded neighbor of “current”:
a. We add the “dist” of “current” to the cost of the edge from “current” to the neighbor.
b. If “dist” from Step 3a is smaller than the neighbor’s “dist” (or if the neighbor’s “dist” is still blank), we update the neighbor’s “dist” to the “dist” that we calculated in Step 3a and set the neighbor’s “last” to be the current node.
4. After we complete Step 3 for all unshaded neighbors of “current,” we shade in “current” and cross out the label “current.”
5. If all nodes are shaded, we go to Step 6. Otherwise, we return to Step 2.
6. We highlight the edge between each node and its “last” node to reveal a shortest-path spanning tree from the origin.
Applications
Using Dijkstra’s algorithm, we can find a shortest path from an origin node to any other node in a network. If you think of your home as the origin node and your destination as some other node in a network, you can determine a good route from your home to any place that you want to go. Suppose that you want to visit several places before returning home. How do you find the best way to visit all of these destinations while minimizing expenses, such as gas, hotels, and time? More abstractly, how can we find a shortest path that passes through all of the nodes in a network and returns to the starting node? This problem, which is an extension of the shortest-path problem, is known as the “Traveling Salesperson Problem”6.
Finding shortest paths is important for solving problems in many different types of networks. For example, shortest paths can improve the efficiency of city planning. Civil engineers can represent a city as a network and determine the best locations to build roads to reduce traffic congestion and the best locations to place irrigation pipes to distribute water to a population [2]. Finding shortest paths also enables the transfer of data from one computer to another at high speeds, allowing massive amounts of information to travel in seconds [1, 2].
There are also many examples of short paths in communication and social networks. For instance, suppose that each person in a social network is a node and that each edge represents a friendship. You can figure out how to connect to a person outside of your friendship groups through the connections of your friends. The shortest paths of connections (such as friendships) between two random people in the United States are shorter than one may think. On average, there are fewer than six steps between an origin person and a destination person in such a path [3]! The typical shortness of shortest paths between people illustrates the “small-world phenomenon,” and these short path lengths also inspired the term “six degrees of separation” [1]. A second example relates to current events. During the COVID-19 pandemic, finding short paths has been useful for limiting exposure to the virus that causes COVID-19. For instance, when moving in a supermarket over the past year and a half, it has been beneficial to find short paths to pick up groceries (while avoiding contact with other people through physical distancing) [4, 5].
Conclusion
Shortest paths are important when traveling from one place to another. They have numerous applications in many types of networks and can help solve a variety of real-world problems. From planning a family vacation to exploring how our world is connected, the study of shortest paths on networks is incredibly important and forms the basis for more complex investigations.
Glossary
Network: ↑ A collection of objects (called “nodes”) and the connections (called “edges”) between them.
Node: ↑ The objects in a network that are connected to other objects. For example, in Figure 1, each location and each street intersection is a node.
Edge: ↑ An object that connects two nodes to each other. For example, when traveling from your home to school, each street is an edge.
Path: ↑ A sequence of edges from an origin node to a destination node.
Cost: ↑ A measure of how much effort it takes to travel along an edge in a network. In real life, a cost may measure distance, time, or something else.
Shortest Path: ↑ A path from an origin node to a destination node that has the lowest total cost among all paths from the origin to the destination.
Shortest-path Spanning Tree: ↑ A portion of a connected network that starts from a given origin node and specifies a shortest path from it to each other node in the network. For example, if a network has 6 nodes, there are 5 such shortest paths in the shortest-path spanning tree. A spanning tree of a network includes all of the network’s nodes. Additionally, because a spanning tree is a type of network known as a “tree,” any pair of nodes in it has exactly one path between them.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
We are grateful to our young readers—Nia Chiou, Taryn Chiou, Zoë Chiou, Tycho Elling, and Sage Hansen—for their many helpful comments. We also thank their family members—Lyndie Chiou, Christina Chow, Tim Elling, and Sterling Hansen—for putting us in touch with them and soliciting their feedback. We are also grateful to Lyndie Chiou, Michelle Lee, Thomas Rexin, and Akrati Saxena for their helpful comments. We also thank our young reviewers and their mentors for their many excellent suggestions. MAP acknowledges support from the National Science Foundation (Grant Number 1922952) through the Algorithms for Threat Detection (ATD) program.
References
[1] ↑ Newman, M. E. J. 2018. Networks, 2nd Edn. Oxford, UK: Oxford University Press..
[2] ↑ Cramer, C., Porter, M. A., Sayama, H., Sheetz, L., and Uzzo, S. (eds). 2015. Network Literacy: Essential Concepts and Core Ideas. Available online at: http://tinyurl.com/networkliteracy
[3] ↑ Milgram, S. 1967. The small-world problem. Psychol Today 1:61–7. doi: 10.1037/e400002009-005
[4] ↑ Brooks, H. Z., Kanjanasaratool, U., Kureh, Y. H., and Porter, M. A. 2021. Disease detectives: Using mathematics to forecast the spread of infectious diseases. Front. Young Minds 9:577741. doi: 10.3389/frym.2020.577741
[5] ↑ Ying, F., and O’Clery, N. 2021. Modelling COVID-19 transmission in supermarkets using an agent-based model. PLoS ONE 16:e0249821. doi: 10.1371/journal.pone.0249821
Appendix
Answer Key
Activity 1: One possible path is (Main, Elm, Scholar). Another possible path is (Main, Oak, Palm, Scholar). A third possible path is (Pine, Maple, Scholar).
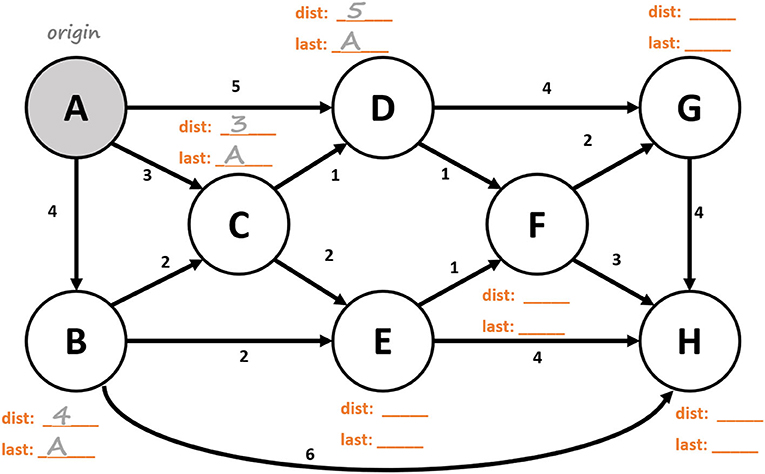
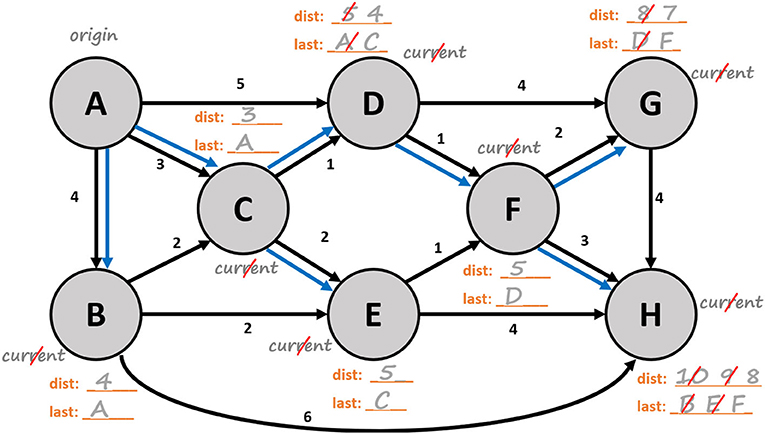
Activity 2: Here is one example of a completed shortest-path spanning tree for the network in Figure 3. Follow along with our explanation in Video 2.
- Video 2 - Activity 2 Walkthrough: Follow along with this video explanation of finding a shortest-path spanning tree for the network in Figure 3.
- You can download a printable version of Figure 3 (it is called “Activity 2 Worksheet”) from https://drive.google.com/file/d/1rNONK-cmy4gq_aCJRnAYpe9Y2HSeq2A1/view.
Footnotes
[1] ↑ Wikipedia. 2020. Shortest path problem. Available online at: https://en.wikipedia.org/wiki/Shortest_path_problem (accessed August 20, 2020).
[2] ↑ When pronouncing the name Dijkstra, the “j” is silent.
[3] ↑ Code.org. 2020. U2L07 Activity guide—Dijkstra’s shortest path algorithm. Available online at: https://docs.google.com/document/d/15N7aHAoWG1_9VIcDHNZRygzFK0hle-EHlmHu0PZI8D4/view (accessed August 20, 2020).
[4] ↑ Wikipedia. 2020. Edsger W. Dijkstra. Available online at: https://en.wikipedia.org/wiki/Edsger_W._Dijkstra (accessed August 20, 2020).
[5] ↑ You can download a printable version of Figure 3 from https://drive.google.com/file/d/1rNONK-cmy4gq_aCJRnAYpe9Y2HSeq2A1/view.
[6] ↑ See https://www.youtube.com/watch?v=q8nQTNvCrjE&t=35s.
