תַקצִיר
מחקרים מראים שאדם ממוצע שואל כ-20 שאלות ביום! כמובן, חלק מהשאלות האלה יכולות להיות פשוטות, כמו לשאול את המורה שלכם אם אתם יכולים ללכת לשירותים, אולם חלק יכולות להיות מאתגרות יותר. זה המקום שבו סטטיסטיקה נכנסת לתמונה! סטטיסטיקה מאפשרת לנו להסיק מסקנות מאוסף נתונים, ולעיתים קרובות היא מכונה “מדע הנתונים”. היא גם יכולה לסייע לאנשים בתעשייה לענות על שאלות המחקר או השאלות העסקיות שלהם, ויכולה לחזות תוצאות, כמו למשל להראות מה הדבר הבא שתרצו לראות ביישׂומון הווידיאו שלכם. עבור מדענים חברתיים, כמו פסיכולוגים, סטטיסטיקה היא כלי שמסייע לנו לנתח נתונים ולענות על שאלות המחקר שלנו.
שאילת שאלות מחקר
מדענים שואלים מגוון שאלות שאפשר לענות עליהן בעזרת סטטיסטיקה. לדוגמה, חוקרים בפסיכולוגיה יכולים להתעניין באופן שבו מבחנים משפיעים על כמות השינה של תלמידים בלילה שלפני המבחן. פסיכולוגים, ביולוגים והרבה מדענים אחרים מתעניינים במענה על שאלות לגבי אוכלוסייה, או קבוצה של פרטים. לדוגמה, ביולוגים יכולים להתעניין בחקירת סוג מסוים של ציפור כאוכלוסיית מחקר, פסיכולוגים התפתחותיים יכולים להתעניין בחקירת ילדים בני 3 עד 6, ומדענים קליניים יכולים להתעניין במטופלים עם מגוון מחלות. סוג הניתוח הסטטיסטי שצריך לעשות תלוי בשאלה שנשאלת, ובאלה משתנים נמדדים. משתנים הם גורמים, תכונות, או מצבים שיכולים להתקיים בכמויות או בסוגים שונים, כמו גובה, גיל, או טמפרטורה.
דגימה מאוכלוסייה
כאשר עונים על שאלות מחקר, לעיתים קרובות אי אפשר לאסוף מידע מכל הפרטים באוכלוסייה שאנו מתעניינים בה. לדוגמה, כשבוחנים את ההשפעות של שינה על ביצועים במבחנים, איננו יכולים לאסוף מידע על השינה ועל תוצאות המבחנים של כל התלמידים בעולם! זו הסיבה לכך שאנו אוספים מידע מדגימה של פרטים שמייצגים בצורה הטובה ביותר את האוכלוסייה הרלוונטית. חשוב שהמאפיינים בדגימה שלנו יהיו דומים למאפיינים של כל האוכלוסייה. מדענים חברתיים מוודאים שהדגימות שלהם בעלות אותו גיל או קבוצה אתנית שהם טיפוסיים לכל האוכלוסייה. אם איננו מוודאים שלדגימות שלנו יש את אותו סוג המאפיינים שיש לכל האוכלוסייה, יכולות להיות בעיות בתשובה על שאלות המחקר שלנו (ראו איור 1).
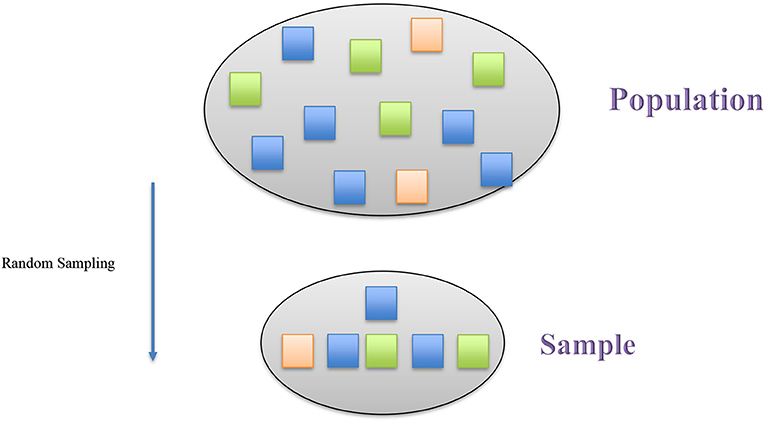
- איור 1 - דגימה אקראית היא דרך לבחור דגימה כך שהיא תייצג את האוכלוסייה בצורה מדויקת.
- בדגימה אקראית, לכל פרט באוכלוסייה יש סיכוי זהה להיבחר לדגימה. בדוגמה הזו, כל צבע בתוך האוכלוסייה גם נמצא בדגימה, והיחסים של כל צבע מיוצגים בדגימה גם כן.
לדוגמה, בואו נגיד שווטרינרית רוצה לחשב את ממוצע המשקל של כל הכלבים. היא אוספת דגימות משקל מחמישה כלבים, מוצאת את ממוצע המשקל של הדגימה שלה, ומסיקה שהמשקל הממוצע של כל הכלבים הוא בין 5 ל-10 קילוגרמים. אם אתם אוהבים כלבים, אתם עשויים לחשוב שמשהו לא בסדר עם המספר הזה. חלק מהכלבים גדולים יותר, אז אתם יכולים לצפות שהממוצע יהיה גבוה יותר. מה אם הווטרינרית אספה דגימה של כלבי צ’יוואווה בלבד? במקרה הזה, בהחלט איננו יכולים להגיד שכל הכלבים שוקלים בין 5 ל-10 קילוגרמים; הדגימה הכילה רק סוג כלבים אחד, ולא ייצגה את כל סוגי הכלבים. אם הווטרינרית הייתה מבצעת דגימה שמייצגת טוב יותר את האוכלוסייה של כל הכלבים, ממוצע המשקל שהיא הייתה מודדת מהדגימה היה ככל הנראה שונה מאוד.
שיטת מפתח לבחירת פריטים לדגימה כדי שייצגו הכי טוב את האוכלוסייה נקראת דגימה אקראית. מדענים משתמשים בדגימה אקראית במטרה להבטיח שלכל פרט באוכלוסייה יש סיכוי שווה להיבחר, וזה מבטיח שהדגימה הכי דומה לאוכלוסייה הכללית.
הערכה מדגימה
ברגע שמדענים מבצעים את הדגימה הם רוצים להסיק מסקנות על הדגימה שלהם, ולהכליל את הממצאים לאוכלוסייה הרחבה יותר. לדוגמה, מדען עשוי לרצות לדעת את מספר שעות השינה הממוצע בלילה של ילדים בני 12, או את ממוצע הגובה של תיכוניסטים בארצות הברית. כדי להעריך את הערך של משתנה באוכלוסייה (כמו גובה ממוצע), מדענים מחשבים אומד נקודתי לדגימה. אומד נקודתי הוא מספר שמעריך את הערך האמיתי של משתנה באוכלוסייה, ולעיתים קרובות האומד הנקודתי הוא ממוצע. לדוגמה, אם אנו רוצים למצוא את מספר הילדים הממוצע בכל בית בעיר שיקגו, אנו צריכים לבצע דגימה אקראית של משפחות בשיקגו, ולשאול כל משפחה כמה ילדים גרים בבית. לאחר מכן, באמצעות המידע הזה, אנו צריכים לחשב את מספר הילדים הממוצע בבתים האלה כדי לחשב את האומד הנקודתי שלנו. אנו יכולים להניח שמספר הילדים הממוצע בדגימה שלנו דומה מאוד לממוצע הילדים בכל הבתים בשיקגו (איור 2).

- איור 2 - במקום ללכת לכל בית בשיקגו כדי להבין מהו מספר הילדים הממוצע בבית, מדענים מבצעים דגימה.
- כאן, מספר הילדים בכל בית בדוגמה נאסף, וממוצע הדגימה חושב. מדענים מצאו באמצעות מה שנקרא אומד נקודתי, שבשיקגו יש בממוצע שני ילדים בכל בית.
מדידות ושיטות דגימה לעולם לא יכולות להיות מדויקות, כך שמדענים לעיתים קרובות משתמשים ברווח בר-סֶמֶך סביב לאומד הנקודתי, כדי להראות טווח ערכים שככל הנראה מכילים את הממוצע של משתנה באוכלוסייה. כדי לחשב את הרווח בר-סמך, מדענים צריכים קודם כל לחשב את שׁוּלֵי הטעות. שולי הטעות הם כמות מחושבת שמחוברת לאומד נקודתי ומחוסרת ממנו. זו דרך לייצג בצורה מספרית את טעויות החישוב בדגימה מהאוכלוסייה (כמו למשל כשהדגימה לא לחלוטין מייצגת את האוכלוסייה).
בואו נתרגל חישוב של רווח בר-סמך! דמיינו שאנו אוספים דגימה של 49 תלמידים למחקר על שינה, ואנו מוצאים ממוצע של כמות שעות שינה בלילה שעומד על 10.5 שעות (זהו האומד הנקודתי שלנו). לאחר מכן, אנו צריכים להבין מהי סטיית התקן, שהיא ממוצע המרחקים בין כל נקודת מידע של בן אדם לבין הממוצע הכולל. כאשר סטיית התקן קטנה, משמעות הדבר שמרבית הנקודות קרובות לערך של הממוצע, וסטיית תקן גדולה משמעותה שהנתונים מפוזרים יותר על פני ערכים שונים. בדוגמה שלנו, בואו נגיד שסטיית התקן היא 1.5 שעות. עכשיו אנו צריכים לחשב את שולי הטעות, באמצעות הנוסחה:

בנוסחה הזו, s מייצגת את סטיית התקן (1.5 שעות), ו-n מתייחסת למספר נקודות הנתונים בדגימה שלנו (49 אנשים). אנו מחליפים את הסמלים בערכים המתאימים, ומחשבים את שולי הטעות שלנו שיוצאת 0.42 שעות שינה. כדי להשלים את חישוב הרווח בר-סמך, אנו מוסיפים את שולי הטעות לאומד הנקודתי שלנו ומחסירים אותם ממנו, כדי לקבל את הגבולות העליון והתחתון של הרווח בר-סמך. פסיכולוגים בדרך כלל משתמשים ברווח בר-סמך של 95% כדי לחשב את שולי הטעות, מה שאומר שאנו יכולים להיות בטוחים שב-95% מהזמן הרווח בר-סמך שלנו מכיל את ממוצע האוכלוסייה האמיתי. הרווח בר-סמך שלנו עבור אומד נקודתי בדוגמה הזו יהיה 10.5 ± 0.42 שעות, או 10.08 ו-10.92. משמעות הדבר היא שב-95% מהזמן מספר שעות השינה שתלמידים ישנים באוכלוסייה הכללית הוא בין 10.08 לבין 10.92 שעות (איור 3).
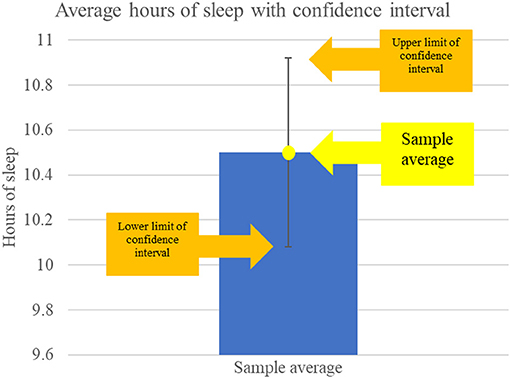
- איור 3 - רווח בר-סמך מראה לנו את טווח הערכים שככל הנראה מכילים את הערך האמיתי של משתנה באוכלוסייה.
- הדוגמה הזו מראה את ממוצע שעות השינה בדגימה שלנו (10.5 שעות). הסרגל מראה רווח בר-סמך של 95% סביב לממוצע, עם 0.42 שעות שחוברו לממוצע וחוסרו ממנו כדי לקבל את שולי הטעות. הרווח בר-סמך מראה שממוצע שעות השינה האמיתי של תלמידים בכל האוכלוסייה הוא בין 10.08 לבין 10.92 שעות.
מדענים יכולים להקטין את שולי הטעות בכמה דרכים, כדי לוודא שההערכה של האוכלוסייה מדויקת יותר. דרך אחת היא לקחת יותר פרטים בדגימה, כך שהדגימה תהיה מייצגת יותר ביחס לאוכלוסייה. דרך אחרת להקטין את שולי הטעות היא לוודא שאיסוף הנתונים הוא כמה שניתן חסר טעויות, כדי להפחית את שוֹנוּת הנתונים, כמו למשל לוודא שכל מכשירי המדידה (כמו משקלים, סקרים וסרגלים) מדויקים במדידה שלהם. ככל שהדגימה מייצגת טוב יותר את האוכלוסייה, באמצעות שימוש בדגימה אקראית ובשיטות טובות לאיסוף נתונים, כך שולי הטעות קטנים והרווח בר-סמך היה מדויק יותר בהערכת הערך האמיתי באוכלוסייה.
שאילת שאלות מחקר מורכבות יותר
לעיתים מדענים רוצים להתקדם מעבר לתיאור חישובים פשוטים כמו ממוצע גבהים או גילאים באוכלוסיות שלהם, כדי להבין היבטים מורכבים יותר באוכלוסיות שלהם. בואו נגיד שאנו מתעניינים לא רק לראות כמה שעות תלמידים ישנים, אלא אנו גם רוצים לדעת בכמה תוצאות המבחנים ירדו אחרי אובדן מספר שעות שינה בלילה הקודם. גדלי אפקט הם ערכים שמעריכים את גודל התופעה, או את המידה שבה משתנה אחד (כמו כמות שעות השינה) משפיע על משתנה אחר (כמו התוצאות במבחן). לדוגמה, אם שינה של 3 שעות מורידה את ציון המבחן בכמה נקודות בהשוואה ל-9 שעות שינה, אתם יכולים שלא לדאוג יותר מדי לגבי אובדן שעות שינה. אומנם יש הבדל בתוצאה, אך לא הבדל גדול. אולם אם אחרי שאיבדתם 6 שעות שינה תוצאת המבחן ירדה משמעותית, זה יכול להשפיע מאוד על הציון הסופי שלכם. במקרה הזה, אתם ככל הנראה תסכימו שההשפעה של אובדן שינה על הציון במבחן היא חשובה.
ישנן דרכים שוֹנוֹת לחשב את גודל האפקט, כתלות בשאלת המחקר ובאיזה סוג סטטיסטיקה המדענים משתמשים. ברגע שמדענים מחשבים את גודל האפקט, הם יכולים להעריך אם האפקט קטן, בינוני, או גדול. גדלי האפקט מאפשרים למדענים, כמו גם לאנשים אחרים, לסקור את הממצאים, ולהבין טוב יותר את ההשפעות של משתנים מסוימים על משתנים אחרים באוכלוסייה.
מסקנות
מדענים שואלים הרבה סוגי שאלות שונים, וישנן הרבה דרכים שבהן סטטיסטיקה יכולה לענות על השאלות האלה. דוגמאות של סטטיסטיקה שדיברנו עליהן במאמר הזה הן דרכים שבהן מדענים חברתיים יכולים לענות על שאלות פשוטות ממדגמים. אולם סטטיסטיקה לא מוגבלת רק לתחום או לנושא מחקר מדעי אחד. סטטיסטיקה סייעה למדענים לדעת אם תרופות צפויות לרפא מחלות, וסייעה למהנדסים להבין את רמת הבטיחות של הרכב שאתם נוסעים בו. זה לא נעצר כאן; ישנן שאלות רבות מִסְפוֹר שאנו יכולים לענות עליהן באמצעות סטטיסטיקה.
מילון מונחים
אוכלוסייה (Population): ↑ קבוצה מובחנת של פרטים שמדענים רוצים לענות על שאלות לגביה.
משתנה (Variable): ↑ גורם, תכונה או מצב שקיים בכמויות שונות או בסוגים שונים, ושנמדד במחקר.
דגימה אקראית (Random Sampling): ↑ דרך לבחור פרטים מאוכלוסייה, שמבטיחה כי הסיכוי לבחור כל פרט הוא שווה.
אומד נקודתי (Point Estimate): ↑ הערכה של ערך מסוים באוכלוסייה, כמו למשל ממוצע.
רווח בר-סמך (Confidence Intervals): ↑ טווח ערכים סביב לאומד נקודתי שככל הנראה מכיל את הערך האמיתי של משתנה באוכלוסייה.
שולי הטעות (Margin of Error): ↑ כמות מחושבת שמחוברת לאומד נקודתי או מחוסרת ממנו, אשר מובאת בחשבון עבור טעויות חישוב.
סטיית תקן (Standard Deviation): ↑ ממוצע המרחקים שבין כל נקודת מידע לבין הממוצע הכולל.
גודל האפקט (Effect Size): ↑ אומר לנו כמה הבדל יש בין ממוצעים של משתנים.
הצהרת ניגוד אינטרסים
המחברים מצהירים כי המחקר נערך בהעדר כל קשר מסחרי או פיננסי שיכול להתפרש כניגוד אינטרסים פוטנציאלי.
קריאה נוספת
Cumming, G. 2013. Understanding the New Statistics: Effect Sizes, Confidence Intervals, and Meta-Analysis. New York, NY: Routledge.
