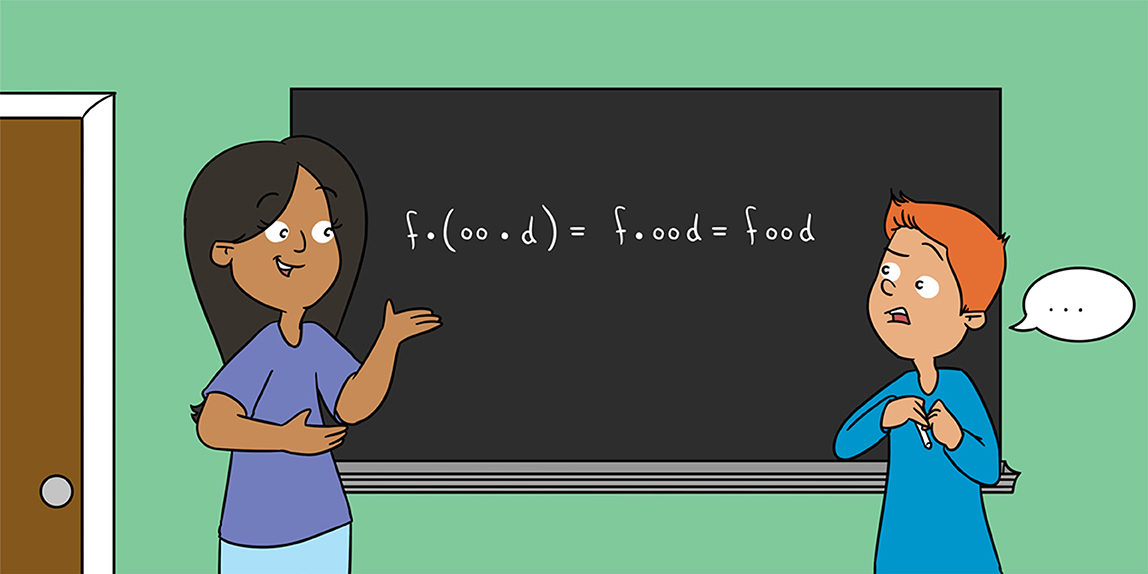Abstract
Algebra is often introduced as arithmetic done with letters. In this article, we follow this analogy and see where it takes us. We ask questions, such as: If “SNAPE = SNAKE,” can we conclude that “P = K”? Here is the spoiler: the path takes us into what mathematicians call group theory, a subfield of algebra that studies symmetry, and allows us to say interesting things about various languages like English and Swedish (and one very important fact about algebra itself).
What Is Algebra Really?
Everybody is introduced to algebra at some point in school mathematics. Algebra comes to us gradually. First, we solve basic arithmetic problems. For example, we might be offered the expression:
We think about our arithmetic facts and fill in the square with 8. Pretty soon, the square changes places and we see:
We know what is going on, and we say the square has to be 5 this time.
When teachers, textbook writers, and curriculum developers decide we are ready for it, the boxes disappear, getting replaced by letters. So, in a class called Algebra, a student might see:
To solve this problem, one “isolates the variable,” applying the same mathematical operation on both sides of the equality sign (“subtract 3”). This might sound fancy, but the problem is actually the very same as the one before it. The box is now a letter; that is the only difference.
In some very basic sense then, school algebra is doing arithmetic with letters. This is actually an incomplete, and somewhat inaccurate, definition of algebra, but it will suffice for now.
If Algebra is About Letters, What Can it Tell us About English?
In algebra class, we are soon working with more and more complicated expressions involving variables and numbers together, such as:
“Isolating the variables” gives us:
If we are told that x = 3, we can plug in the value for x and see:
Dividing both sides by 3 yields y = 2.
Eventually, we get really good at noticing common factors on both sides of the equality sign and canceling them out: 4x = 16 becomes x = 4, 11y = 33 becomes y = 3, and so on.
Could we do all of algebra with only letters, the way we do arithmetic with only numbers? In that case, letters could even be actual letters, not placeholders. What would it mean to say that two expressions are equal to one another in this scenario? For example, Professor Severus Snape of Hogwarts is a famous Slytherin, so it makes sense to say that “SNAPE = SNAKE.” We could also say:
or,
This last one is tricky, because “my” is always context dependent. For example, if Gizem is reading this sentence, “my favorite food” will mean “Gizem’s favorite food” and the resulting sentence will be a true statement. However, if her sister were reading the same sentence, she would be asserting that Gizem’s sister’s favorite food is ice cream, which is definitely not a true statement (Yes, there are people who just do not like ice cream. Weird, we know!). One could even consider pronouns to be the ultimate variables. After all, each pronoun takes the place of a noun determined by the context of the earlier conversation.
Another thing we could do using only letters is to make two expressions equal if they sound the same. For example, in English, the letter collection “you” sounds the same as the single letter “u.” So, we could set them equal to one another:
Does your eager algebra eye want to do some cancellations? Do you think you can cancel the “u”s on both sides and get “yo = 1”? Why not? But then “dye = die” gives you “y = i” and so on. How far can you go? And just what does “y = i” mean?
What is Going on? A Group Theory Primer
In mathematics, group theory is the field of algebra that studies symmetry using certain algebraic structures called groups. A group is a bag of objects (see also [1]) together with a way of taking two objects from the bag to make another object that is also in the bag. The objects can be anything: numbers, words, or even ice cream cones. The “way” is called an operation and is often written “•”: if object1 and object2 are two objects in the bag,
is the object in the bag we make from object1 and object2 with the operation “•.” We can form yet another object by first taking the object object1 • object2 and then the object object3 from the bag, to get the object
But what if we took instead object1 first and then
In a group, the resulting object is the same! In other words, we require that what is called the associative law holds:
We also require that there is a special object in the bag, let us call it theone, since it is so special, such that for any object object in the bag,
Our last requirement is that we should be able to cancel objects on both sides of “=” to get the resulting object theone. This can be expressed as follows: we want any object object in the bag to have a buddy in the bag called an inverse, say inverseobject, such that
That’s it! A bag of objects with an operation that satisfies these three requirements is called a group.
Example 1 We could take the bag of objects to be all the numbers (positive, negative, and zero) and “•” to be “+.” For example, 3 + 4 = 7 and 7 + 2 = 9, so (3 + 4) + 2 = 7 + 2 = 9. We also have 4 + 2 = 6 and 3 + 6 = 9, so 3 + (4 + 2) = 3 + 6 = 9. In other words, (3 + 4) + 2 = 3 + (4 + 2). This holds true for all numbers in our bag. Our special object theone turns out to be the number 0. Since 7 + (-7) = 0, the inverse of 7 has to be - 7. Can you figure out what the inverse of any number must be?
Example 2 Let us try to make a group out of the letter x. We start by putting x in our bag of objects. In order to make this a group, we also need to add the special object theone to our bag. Instead of writing theone, which is a bit cumbersome, we use the symbol 1. Last, we also need to add the inverse of x. We put a hat on x and simply say that this new letter, , is the inverse of x. This means that with x, , and 1 in our bag, x • =1. Is this a group? No, not yet. For example, x • x also needs to be in our bag, so we simply add it and its inverse • as well. Continuing like this and assuming that the associative law holds, we get the so-called group generated by x.
Example 3 Suppose that we take the group generated by x as described in Example 2 and add the rule x = 1. If we replace x by 1 in x • = 1, we get 1 • = =1. We also get x • x = 1 • 1 = 1. In fact, all objects in our bag must be equal to 1. In other words, our bag contains only one object, 1. From the definition, the bag in a group needs to have at least one object in it, theone. Therefore, this must be the smallest group possible, so it is called the trivial group.
Example 4 - Let us explore a more visual example. Consider the Scrabble tile for the letter R:

Photo: Per Bäck.
This tile can be rotated 90° clockwise to give us

Photo: Per Bäck.
If you rotate it 90° more, you get:
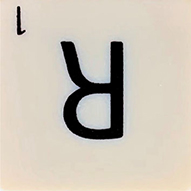
Photo: Per Bäck.
Another 90° rotation gives you:

Photo: Per Bäck.
and a final 90° rotation will get you back to the original tile. This is a nice example of a group. Each of these operations can be reconstructed from the single clockwise rotation by 90°. If we set x to be the “rotate clockwise by 90°” operation, then the group we get is the bag containing x, x2, x3, and x4; this last one is the same as theone, or in this context, the “do-nothing” operation. Do you see what the inverses are?
Homophonic Groups
Can we make a group out of the whole alphabet? The English alphabet consists of 26 letters a,b,c,…,z. We invent the inverse English alphabet to be the letters of the English alphabet with hats on them, ,,,…,. We form all possible words from the letters in the two alphabets and put them in a bag. By a word, we mean any combination of letters, so qwrtasdf, brain, d, and foo are all words in our bag. Whenever a letter lies immediately next to its inverse letter in a word, we cancel the two letters. This means that
and
We also invent an operation • on the bag of words to be that of gluing two words together to make a new word, so that
and
This also means that
the word consisting of no letters at all—the empty word! Continuing, the operation • obeys the associative law. For example,
and
This almost looks like a group where the special object is the empty word! However, we need not only the letters to have inverses, but all the words as well. This works if we say that the inverse of a word is the word spelled backwards and with a hat on each letter. For example, the inverse of yo is since then
Just as in Example 2, we could use the symbol 1 for the special object (the empty word in this case), so that
The above group is called the free group on the English alphabet. Free, because it is the freest way one can make a group out of the English alphabet.
Now, suppose that we add the rule that two words are equal if they sound the same, as we suggested at the end of the second section. Then this means that
We can cancel the “u”s by using the operation • together with on each side. On the left-hand side, we get
and on the right-hand side
so yo = 1.
Words that sound the same are called homophones, and the free group on the English alphabet where homophones are equal is called the homophonic group of English. The word you and the letter u are therefore the same in the homophonic group of English, and by the above calculations, so are yo and the empty word (for which we used the symbol 1). Mathematicians have shown that the homophonic groups of English and French are the groups with just the empty word in them—the trivial group [2]. Other authors have shown that the homophonic group of German is the trivial group, while those of Korean and Turkish are not [3].
Swedish, Anyone?
Why not learn Swedish while doing group theory? In fact, we will see that it is trivial! The Swedish alphabet has 29 letters in it: the 26 letters that form the English alphabet together with the three funny-looking letters å,ä, and ö. By using a standard dictionary like [4], we will see that the homophonic group of the Swedish language is the trivial group. First, we use something that cannot be found in the Swedish Academy’s dictionary [4], but is well-known to all Swedish mathematicians, namely that om and omm are pronounced the same. In other words,
so by canceling om on both sides, m = 1. Continuing,
so e = h = l = n = o = 1. We also have
which gives us b = d = g = p = v = 1. Since
we have f = v = 1, j = g = 1, å = o = 1, ä = e = 1. Now,
and so a = 1a = oa = å = 1, i = i1 = ig = ej = 1, k = j = 1, and r = 1rr gives us r = 1. Moreover,
so we must have c = c1 = ch = k = 1, w = w1 = wie = vi = 1, and y = 1y = ay = ej = 1. Now,
and so s = c = 1, t = t1 = tj = ch = 1. We have
which gives us x = ks = 1, z = z1 = zo = s = 1. We also have
so we get u = 1u1 = sioux = so = 1. At last,
and therefore q = q1 = qu = ck = 1 and ö = oeu = 1. We have shown that all the 29 letters must be equal to 1. Since the only word we can form from 1 is 1, we have shown that the homophonic group of Swedish is trivial!
So What?
Why is all of this important? Here is an argument that might appeal to many mathy folks: Since any word in the trivial group is the empty word 1 and English is trivial, algebra = 1 and awesome = 1. Therefore, algebra = awesome. Now isn’t that something?
On a more serious note, the homophonic group of a language tells us how well the alphabet represents what the language sounds like. English, French, German, and Swedish, whose homophonic groups are all trivial, have many words where different letters are pronounced the same. Korean and Turkish, whose homophonic groups are non-trivial, have younger alphabets whose letters sound more similar to what they do in actual words. In other words, just playing around with letters in fun and seemingly meaningless ways can actually tell us something interesting about languages and their writing systems. Maybe the next time someone asks you what algebra is good for, you can tell them that it can help us understand something as human as language!
If you are excited by this article and want to learn more about groups, there are many books out there that might be good next steps. Alternatively, you might check out this interesting article on more examples of groups [5], or this neat online exploration of one of the most ambitious group theory projects of the twentieth century [6].
Glossary
Group: ↑ A bag of objects together with an operation that takes two objects from the bag to make another object that is also in the bag. The operation needs to obey the associative law, and the special object theone must be in the bag. Last, all objects in the bag must have an inverse that is also in the bag.
Operation: ↑ A way of taking two objects from a bag to form a new object that is also in the bag.
Associative Law: ↑ If “•” is an operation and object1, object2, and object3 are objects in some bag, the associative law says that the object (object1 • object2) • object3 is the same object as object1 • (object2 • object3).
Inverse: ↑ If “•” is an operation and object an object in some bag, the inverse of object, let us call it inverseobject, is an object in the bag such that object • inverseobject = inverseobject • object = theone. Here, theone is the special object in the bag.
Trivial Group: ↑ The smallest group possible, the bag of objects containing only one object, theone.
Empty Word: ↑ The word with no letters in it.
Free Group: ↑ The group made from some alphabet by using the operation of gluing letters together to form words, and then gluing words together to form new words. In the bag of objects are all words possible, including the empty word, which is the special object theone.
Homophonic Group: ↑ The free group on some alphabet where words that sound the same are equal.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
[1] ↑ Bouyer, F. 2018. Infinity and trying to do maths with it. Front. Young Minds 6:61. doi: 10.3389/frym.2018.00061
[2] ↑ Mestre, J. F., Schoof, R., Washington, L., and Zagier, D. 1993. Homophonic quotients of free groups [Quotients homophones des groupes libres]. Exp. Math. 2:153–5. doi: 10.1080/10586458.1993.10504275
[3] ↑ Gangl, H., Karaali, G., and Lee, W. 2019. Homophonic quotients of linguistic free groups: German, Korean, and Turkish. Involve 12:463–74. doi: 10.2140/involve.2019.12.463
[4] ↑ The Swedish Academy. 2020. Svenska Akademiens Ordböcker. Available online at: https://svenska.se/ (accessed October 20, 2020).
[5] ↑ Roney-Dougal, C. 2006. The Power of Groups. Plus Magazine. Available online at: https://plus.maths.org/content/os/issue39/features/colva/index.
[6] ↑ Elwes, R. 2006. An Enormous Theorem: The Classification of Finite Simple Groups. Plus Magazine. Available online at: https://plus.maths.org/content/os/issue41/features/elwes/index