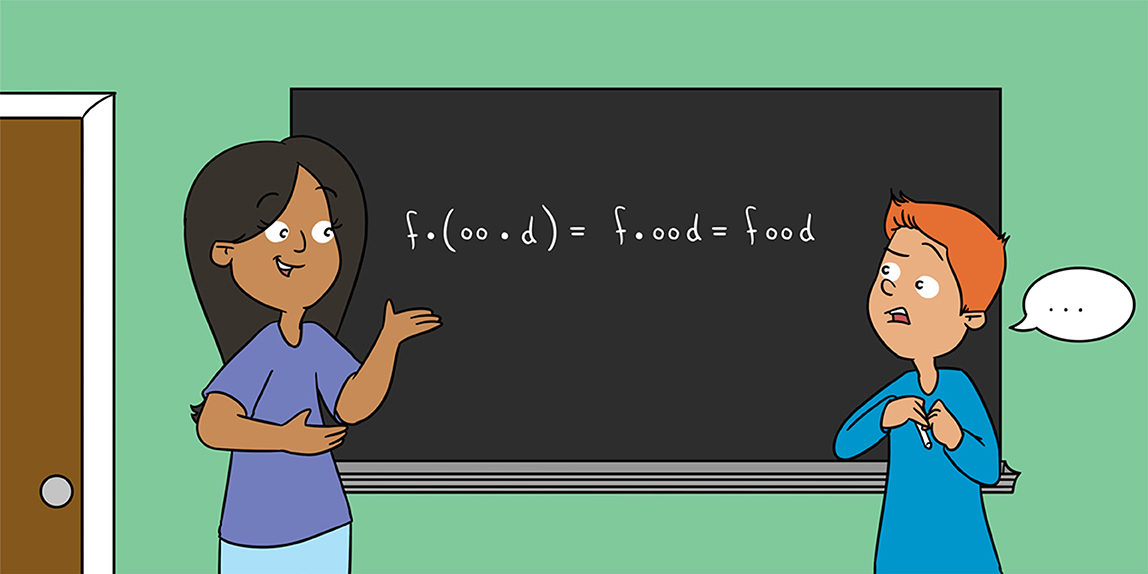תַקצִיר
לעיתים קרובות, אלגברה מוצגת כאריתמטיקה שמבוצעת עם אותיות. במאמר זה נעקוב אחר האנלוגיה הזו, ונראה לאן היא מובילה אותנו. אנו שואלים שאלות כמו: אם “SNAPE = SNAKE,” האם אנו יכולים להסיק ש “P = K?” הנה ספוילר: הדרך תוביל אותנו אל מה שמתמטיקאים מכנים ’תורת החבורות’, תת-תחום של אלגברה שחוקר סימטריה, ומאפשר לנו לומר דברים מעניינים על שפות שונות כמו אנגלית ושוודית, ועובדה אחת חשובה מאוד על האלגברה עצמה.
מהי אלגברה, בעצם?
כולם נתקלים באלגברה בשלב מסוים במתמטיקה של בית הספר. אלגברה מגיעה אלינו בהדרגה. ראשית, אנו פותרים בעיות אריתמטיות בסיסיות. לדוגמה, עשויים להציג לנו את הביטוי:
אנו חושבים על העובדות המתמטיות, וממלאים את הריבוע בספרה 8. מהר מאוד, הריבוע משנה את מיקומו, ומציגים בפנינו את התרגיל:
אנו מבינים את המהלך, ואומרים שהריבוע צריך להיות 5 הפעם.
כאשר מורים, כותבי ספרי לימוד ומפתחי תכני לימודים מחליטים שאנו מוכנים לכך, הריבועים נעלמים, ומוחלפים באותיות. אז, בשיעור שנקרא אלגברה, תלמיד יכול לקבל את התרגיל:
כדי לפתור את הבעיה הזו, צריך “לבודד את המשתנה”, ולבצע את אותה הפעולה המתמטית בשני צידי המשוואה (“להפחית 3”). זה עשוי להישמע מסובך, אולם הבעיה היא אותה בעיה בדיוק כמו הקודמת. הריבוע הוא עכשיו אות; זה ההבדל היחיד.
במובן בסיסי ביותר, אם כן, אלגברה בבית הספר מבצעת אריתמטיקה עם אותיות. זוהי הגדרה לא שלמה ודי לא מדויקת של אלגברה, אך היא בכל זאת מספיקה לעכשיו.
מה אלגברה, המשתמשת באותיות, יכולה לומר לנו על השפה האנגלית?
בשיעור אלגברה, אנו עובדים במהרה עם יותר ויותר ביטויים מסובכים שמערבים משתנים ומספרים יחד, כמו למשל:
“בידוד המשתנים” נותן לנו:
אם אומרים לנו ש- x = 3, אנו יכולים להציב את הערך שלו במשוואה, ולקבל:
חלוקת שני הצדדים פי 3 נותנת y = 2.
בסופו של דבר, אנו נעשים טובים מאוד בהבחנה בגורמים משותפים בשני צידי המשוואה, וביטולם: 4x = 16 נהפך ל-x = 4, 11y = 33 נהפך ל-y = 3, וכן הלאה.
האם נוכל לבצע את האלגברה כולה באמצעות אותיות בלבד, באופן שבו אנו פותרים אריתמטיקה עם מספרים בלבד? במקרה כזה, אותיות יכולות להיות אותיות אמיתיות, ולא רק שומרות מקום. מהי המשמעות של שני ביטויים השווים זה לזה במקרה האמור? לדוגמה, פרופסור סוורוס סנייפ (דמות בסדרת ספרי הארי פוטר) מהוגוורטס (בית הספר לכישוף וקוסמות בספרים) הוא איש סלית’רין מפורסם (אחד הבתים בהוגוורטס), ולכן הגיוני לומר ש-“SNAPE = SNAKE” (סנייפ = נחש). אנו יכולים גם לומר:
או:
המשוואה האחרונה היא מורכבת, מאחר ש“עליי” הוא תלוי הֶקְשֵׁר. לדוגמה, אם Gizem קוראת את המשפט הזה, משמעותו של “המזון האהוב עליי” תהיה “המזון האהוב על Gizem,” ותוצאת המשפט תהיה הצהרה נכונה. אולם אם אחותה הייתה קוראת את אותו המשפט, המשמעות הייתה שהמזון האהוב על אחותה של Gizem הוא גלידה, וזו בהחלט לא הצהרה נכונה (כן, מוזר ככל שזה יישמע, יש אנשים שלא אוהבים גלידה!). מישהו יכול אפילו לשקול כינויי גוף כמשתנים אולטימטיביים. אחרי הכול, כל כינוי גוף מחליף את מקומו של שם עצם שנקבע על ידי ההקשר מהשיח הקודם.
דבר נוסף שאנו יכולים לעשות באמצעות אותיות בלבד הוא להשוות בין ביטויים על בסיס איך שהם נשמעים. לדוגמה, באנגלית אוסף האותיות “you” נשמע אותו דבר כמו האות הבודדת .“u” לכן, אנו יכולים להשוות אותם זה לזה:
האם העין האלגברית שלכם רוצה לערוך ביטולים? האם אתם חושבים שאתם יכולים לבטל את ה-“u” בשני הצדדים ולקבל “yo = 1?” מדוע לא? אולם אז, “dye = die” נותן לכם “y = i,” וכן הלאה. כמה רחוק תוכלו ללכת? ומה המשמעות של “y = i?”
היכרות בסיסית עם תורת החבורות
במתמטיקה, תורת החבורות היא תחום באלגברה שחוקר סימטריה באמצעות מבנים אלגבריים מסוימים, שנקראים חבורות. חבורה היא שק של אובייקטים (ראו גם [1]), בשילוב דרך לקחת שני אובייקטים מהשק ולהפוך אותם לאובייקט אחר שגם הוא נמצא בשק. האובייקטים יכולים להיות כל דבר: מספרים, מילים, או אפילו גביעי גלידה. ה“דרך” נקראת פעולה, והיא לעיתים קרובות נכתבת בתור “•:” אם object1 ו-object2 הם שני אובייקטים בשק,
הוא האובייקט בשק שנוצר מ- object1 ו-object2 עם הפעולה “•.” אנו יכולים ליצור אובייקט אחר על ידי לקיחת האובייקט object1 • object2 ואז את האובייקט object3 מהשק, ולקבל את האובייקט:
אולם מה אם ניקח קודם את object1 ואז את:
בחבורה, האובייקט שמתקבל הוא זהה! במילים אחרות, אנו דורשים את קיומו של מה שנקרא חוק אסוציאטיביות:
אנו גם דורשים שיהיה אובייקט מיוחד בשק, בואו נקרא לו theone (“האחד”), מאחר שהוא כל כך מיוחד, כך שעבור כל אובייקט object בשק:
הדרישה האחרונה שלנו היא שנוכל להיות מסוגלים לבטל אובייקטים משני צידי ה“=” כדי לקבל את האובייקט theone. אפשר לבטא זאת באופן הבא: אנו רוצים שלכל אובייקט object בשק יהיה חבר בשק שנקרא הופכי, שנכנה אותו inverseobject (“אובייקט הופכי”), כך ש:
זהו זה! שק של אובייקטים עם פעולה שמקיימת את שלוש הדרישות האלה נקרא חבורה.
דוגמה 1: אנו יכולים לקחת שק של אובייקטים בתור כל המספרים (חיוביים, שליליים ואפס) עם הפעולה “•” שהיא “+.” לדוגמה, 3 + 4 = 7, ו-7 + 2 = 9, אז (3 + 4) + 2 = 7 + 2 = 9. אנו יכולים שגם יהיה לנו 4 + 2 = 6 ו- 3 + 6 = 9, ואז 3 + (4 + 2) = 3 + 6 = 9. במילים אחרות, (3 + 4) + 2 = 3 + (4 + 2) +. זה נכון לכל המספרים בשק שלנו. האובייקט המיוחד theone הופך להיות המספר 0. מאחר ש 7 + (-7) = 0, ההופכי של 7 צריך להיות 7.- האם תוכלו לפענח מה צריך להיות ההופכי של כל מספר?
דוגמה 2: בואו ננסה לייצר קבוצה מהאות x. אנו מתחילים בכך שאנו שׂמים את ה- x בשק האובייקטים שלנו. כדי להפוך זאת לקבוצה, אנו צריכים להוסיף גם את האובייקט המיוחד theone לשק שלנו. במקום לכתוב theone, שזה קצת מסורבל, אנו משתמשים בסמל 1. לבסוף, אנו צריכים להוסיף גם את ההופכי של x. אנו שמים כובע על x ופשוט אומרים שהאות החדשה הזו, , היא ההופכית של x. משמעות הדבר היא שעם x, , ו-1 בשק שלנו, . האם זוהי חבורה? עדיין לא. לדוגמה, x • x גם צריך להיות בשק שלנו, ולכן אנו פשוט מוסיפים אותו, וגם את ההופכי שלו . אם ממשיכים כך ומניחים שחוק האסוציאטיביות שלנו תקף, אנו מקבלים חבורה שנוצרת על ידי x.
דוגמה 3: נניח שאנו לוקחים חבורה שנוצרת על ידי x כפי שתואר בדוגמה 2, ומוסיפים את החוק 1 = x. אם נציב את x במקום 1 במשוואה , נקבל . אנו מקבלים גם x • x = 1 • 1 = 1. למעשה, כל האובייקטים בשק שלנו צריכים להיות שווים ל-1. במילים אחרות, השק שלנו מכיל רק אובייקט אחד, 1. מתוך ההגדרה, השק הוא קבוצה שצריכה שיהיה בה לפחות אובייקט אחד, theone. לפיכך זו צריכה להיות הקבוצה הקטנה ביותר האפשרית, ולכן היא נקראת קבוצה טריוויאלית.
וידאו 1. דוגמה 4. בואו נחקור דוגמה ויזואלית יותר. הסתכלו על אריח השבץ-נא עבור האות R:

(תמונה: Per Bäck)
אפשר לסובב את האריח הזה ב-90 מעלות ימינה, ולקבל:

(תמונה: Per Bäck)
אם תסובבו אותו מעלות נוספות, תקבלו:
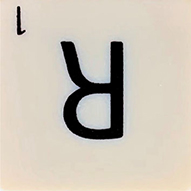
(תמונה: Per Bäck)
וסיבוב נוסף ב-90 מעלות ייתן לכם:

(תמונה: Per Bäck)
סיבוב אחרון מעלות יחזיר אתכם חזרה לאריח המקורי. זוהי דוגמה נחמדה של חבורה. כל אחת מהפעולות האלה יכולה להיות מורכבת מסיבוב בודד מעלות עם כיוון השעון. אם נגדיר את x להיות הפעולה “סיבוב מעלות עם כיוון השעון”, אז החבורה תהיה שק שמכיל את האובייקטים, x2, x x3, ו-x4; האובייקט האחרון זהה או בהקשר הזה פעולת “עשה-כלום”. האם אתם רואים מהם ההופכיים במקרה הזה?
קבוצות הומופוניות
האם אנו יכולים ליצור חבורה מהאלפבית כולו? האלפבית האנגלי מכיל 26 אותיותa, b, c…, z. אנו ממציאים את האלפבית האנגלי ההופכי להיות האותיות באלפבית האנגלי עם כובע מעליהן, . אנו יוצרים את כל המילים האפשריות מהאותיות בשני האלפביתים, ושמים אותן יחד בשק. ב“מילה”, אנו מתכוונים לכל צירוף של אותיות, כך ש-, brain, d, ו-foo, כולן מילים בשק שלנו. בכל פעם שאות מופיעה מייד ליד האות ההופכית שלה במילה, אנו מבטלים את שתי האותיות. זה אומר ש:
ו-
אנו גם ממציאים פעולה • על שק המילים להיות הפעולה שמדביקה שתי מילים יחד כדי ליצור מילה חדשה, כך ש:
ו-
זה גם אומר ש:
המילה שאינה מכילה אותיות כלל – המילה הריקה! ממשיכים, כך שהאופרטור • מקיים את חוק האסוציאטיביות. לדוגמה:
ו-
זה כמעט נראה קבוצה שבה האובייקט המיוחד הוא מילה ריקה! אולם אנו צריכים שלא רק לאותיות יהיו הופכיים, אלא גם לכל המילים. זה עובד אם אנו אומרים שכל הופכי של מילה היא מילה שמאויתת לאחור עם כובע על כל אות. לדוגמה, ההופכי של yo הוא מאחר שאז:
ממש כמו בדוגמה 2, אנו יכולים להשתמש בסמל 1 עבור האובייקט המיוחד (המילה הריקה במקרה הזה), כך ש:
החבורה שלמעלה נקראת החבורה החופשית של האלפבית האנגלי. חופשית, מאחר שהיא האופן החופשי ביותר שבו אפשר ליצור קבוצה מכל האלפבית האנגלי.
כעת, נניח שאנו מוסיפים את החוק שלפיו שתי מילים שוות אם הן נשמעות אותו הדבר, כפי שהצענו בסוף החלק השני קודם לכן. משמעות הדבר היא ש:
אנו יכולים לבטל את ה-“u”-ים באמצעות שימוש בפעולה • עם בכל צד. מצד שמאל, אנו מקבלים:
ומצד ימין אנו מקבלים:
ולכן yo = 1.
מילים שנשמעות אותו הדבר נקראות הומופונים, והחבורה החופשית של האלפבית האנגלי שבה הומופונים זהים, נקראת חבורה הומופונית של אנגלית. המילה you והאות u הן זהות, לכן, בחבורה ההומופונית של אנגלית, ולפי החישובים שלעיל כך גם yo והמילה הריקה (שעבורה השתמשנו בסמל 1). מתמטיקאים הראו שהחבורות ההומופוניות של אנגלית ושל צרפתית הן חבורות שמכילות את המילה הריקה בלבד – קבוצה טריוויאלית [2]. מחבּרים אחרים הראו שהחבורה ההומופונית של גרמנית היא קבוצה טריוויאלית, בעוד אלה של קוריאנית ושל טורקית הן לא [3].
שוודית, מישהו?
למה לא ללמוד שוודית בזמן שמכירים את תורת החבורות? למעשה, נגלה שזה טריוויאלי! האלפבית השוודי מכיל 29 אותיות: 26 האותיות מהאלפבית האנגלי, עם שלוש אותיות שנראות מצחיק: å, ä, ו-ö. באמצעות שימוש במילון סטנדרטי כמו [4], נראה שהחבורה ההומופונית בשפה השוודית היא קבוצה טריוויאלית. ראשית, נשתמש במשהו שלא נמצא במילון של האקדמיה השוודית [4], אולם הוא ידוע לכל המתמטיקאים השוודים, וזה ש-om ו-omm מבוטאים אותו הדבר. במילים אחרות,
לכן, על ידי ביטול om בשני הצדדים, m = 1. אם ממשיכים:
ולכן: e = h = l = n = o = 1. יש לנו גם:
מה שנותן לנו: b = d = g = p = v = 1. מאחר ש:
ישלנו: f = v = 1, j = g = 1, å = o = 1, ä = e = 1. כעת:
וגם 1a = a = å = oa = ,1 ej = ig = i1 = i = ,1 j = k = 1, ו-r = 1rrנותן לנו r = 1.
ולכן עלינו לקבל c = c1 = ch = k = 1, w = w1 = wie = vi = 1, -ו y = 1y = ay = ej = 1. כעת:
ולכן s = c = 1, t = t1 = tj = ch = 1. יש לנו:
מה שנותן לנו x = ks = 1, z = z1 = zo = s = 1. יש לנו גם:
ולכן אנו מקבלים u = 1u1 = sioux = so = 1. לבסוף:
ולכן q = q1 = qu = ck = 1 ו-ö = oeu = 1. הראינו שכל 29 האותיות צריכות להיות שוות ל-1. מאחר שהמילה היחידה שאנו יכולים ליצור מ-1 היא 1, הראינו שהחבורה ההומופונית של השפה השוודית היא טריוויאלית!
מהי המשמעות של תורת החבורות?
למה כל זה חשוב? הנה טיעון שעשוי לדבר אל הרבה אנשי מתמטיקה: מאחר שכל מילה בקבוצה הטריוויאלית היא המילה הריקה 1 ואנגלית היא טריוויאלית, algebra = 1 ו-awesome = 1. לכן, algebra = awesomes (אלגברה היא מדהימה). נכון שזה משהו?
בטון מעט רציני יותר, הקבוצה ההומופונית של שפה אומרת לנו כמה טוב האלפבית מייצג את האופן שבו השפה נשמעת. אנגלית, צרפתית, גרמנית ושוודית, שהקבוצות ההומופוניות שלהן טריוויאליות כולן, מכילות מילים רבות שבהן אותיות שונות מבוטאות אותו הדבר. קוריאנית וטורקית, שהחבורות ההומופוניות שלהן אינן טריוויאליות, הן בעלות אלפבית צעיר יותר שהאותיות שלו נשמעות הרבה יותר דומות לאיך שהן פועלות במילים עצמן. במילים אחרות, משחק עם אותיות בצורה כיפית שנראית חסרת משמעות יכול לומר לנו משהו מעניין על השפות ועל מערכות הכתיבה שלהן. אולי בפעם הבאה שמישהו ישאל אתכם למה אלגברה מועילה, תוכלו לומר לו שהיא יכולה לסייע להבין משהו אנושי כמו שפה!
אם אהבתם את המאמר הזה, ואתם רוצים ללמוד עוד על חבורות, ישנם ספרים רבים שיכולים להיות טובים לצעד הבא. לחלופין, תוכלו לקרוא את המאמר המעניין הזה על דוגמאות של חבורות [5], או להסתכל על החקירה המגניבה הזו ברשת של אחד מפרויקטי תורת החבורות השאפתניים ביותר במאה העשרים [6].
מילון מונחים
חבורה (Group): ↑ שק של אובייקטים עם פעולה שלוקחת שני אובייקטים מהשק כדי ליצור אובייקט אחר שגם הוא נמצא בשק. הפעולה צריכה לעקוב אחר החוק האסוציאטיבי, והאובייקט המיוחדtheone צריך להיות בשק. לבסוף, כל האובייקטים בשק צריכים להיות עם הופכי שגם הוא נמצא בשק.
פעולה (Operation): ↑ דרך ללקיחת שני אובייקטים משק כדי ליצור אובייקט חדש שגם הוא נמצא בשק.
חוק אסוציאטיביות (Associative Law): ↑ אם “•” היא פעולה ו-object1, object2, ו- object3הם אובייקטים באותו השק, החוק האסוציאטיבי אומר שהאובייקט (object1 • object2) • object3 זהה לאובייקט object1 • (object2 • object3).
הופכי (Inverse): ↑ אם “•” היא פעולה ו-object הוא אובייקט באיזשהו שק, ההופכי של object, בואו נקרא לו inverseobject, הוא אובייקט בשק כך ש-object • inverseobject = inverseobject • object = theone. כאן, theone הוא האובייקט המיוחד בשק.
חבורה טריוויאלית (Trivial Group): ↑ החבורה הקטנה ביותר האפשרית, שק האובייקטים שמכיל מילה אחת בלבד, theone.
מילה ריקה (Empty Word): ↑ מילה שלא מכילה אותיות.
חבורה חופשית (Free Group): ↑ חבורה שמורכבת מאיזשהו אלפבית באמצעות הפעולה של הדבקת אותיות יחד כדי ליצור מילה, ואז הדבקת מילים יחד כדי ליצור מילים חדשות. בשק האובייקטים כל המילים אפשריות לרבּות מילה ריקה, שהיא האובייקט המיוחד theone.
חבורה הומופונית (Homophonic Group): ↑ חבורה חופשית על אלפבית כלשהו שבה מילים שנשמעות אותו הדבר הן זהות.
הצהרת ניגוד אינטרסים
המחברים מצהירים כי המחקר נערך בהעדר כל קשר מסחרי או פיננסי שיכול להתפרש כניגוד אינטרסים פוטנציאלי.
מקורות
[1] ↑ Bouyer, F. 2018. Infinity and trying to do maths with it. Front. Young Minds 6:61. doi: 10.3389/frym.2018.00061
[2] ↑ Mestre, J. F., Schoof, R., Washington, L., and Zagier, D. 1993. Homophonic quotients of free groups [Quotients homophones des groupes libres]. Exp. Math. 2:153–5. doi: 10.1080/10586458.1993.10504275
[3] ↑ Gangl, H., Karaali, G., and Lee, W. 2019. Homophonic quotients of linguistic free groups: German, Korean, and Turkish. Involve 12:463–74. doi: 10.2140/involve.2019.12.463
[4] ↑ The Swedish Academy. 2020. Svenska Akademiens Ordböcker. Available online at: https://svenska.se/ (accessed October 20, 2020).
[5] ↑ Roney-Dougal, C. 2006. The Power of Groups. Plus Magazine. Available online at: https://plus.maths.org/content/os/issue39/features/colva/index.
[6] ↑ Elwes, R. 2006. An Enormous Theorem: The Classification of Finite Simple Groups. Plus Magazine. Available online at: https://plus.maths.org/content/os/issue41/features/elwes/index