Zero, a Hard-Working Hero!

Imagine for a minute what your life would be like without that little circle we use to represent zero!

While we take zero for granted, it is a relatively recent invention. The Babylonians and Romans did not have a way to represent zero with a distinct symbol; nor did the Greeks, who did not think “nothing” was a number. The Mayans living in Central America used the idea of zero [1]¹ in their calendar system, but because they were isolated from other people, their zero did not travel beyond their own civilization. To find the source of zero, we must look elsewhere.

Let us look at numerals used in ancient Babylon, where there was a sophisticated mathematical system over 5,000 years ago. This system was developed and refined from even older systems of writing numbers and making calculations! We know a lot about the Babylonian system, because they wrote on clay tablets that have survived. The Babylonians were good mathematicians and astronomers who used a complicated base 60 system, rather than our base 10 system². In modern mathematics, we still use base 60 for certain functions. For example, think of how we keep time: 60 s in a minute, 60 min in an hour. The Babylonians, like us, used positions (like our base 10 ones, tens, hundreds, thousands) to represent numbers. But using the base 60 system meant that calculations and keeping track of places was exceedingly complicated. In the base 60 system, positions become sixes, sixties, six hundreds, six thousands. Imagine that you are trying to keep track of positions with no symbol for zero to mark the space. That little symbol for zero is very helpful. The Babylonians eventually began to mark the empty column with a space, but just think how easy it must have been to miss a space in columns of numbers. With their complicated system, the Babylonians had to rely on context to understand the meaning of a number. As an example of using context, if someone tells you that something costs four-fifty, you could assume $4.50, if you were thinking about ordering an ice cream, rather than $450, which might seem logical if you were buying an airline ticket.

The Greeks knew of zero as a concept but did not think of it as a number with the same usefulness in mathematics as the numbers 1–9. According to Aristotle, it was not possible to divide by 0 and get a meaningful result, so the Greek system was based on 9 numbers—no zero.

The Romans did not use numerals for calculations, so they did not have the need for a zero to hold a place or keep a column empty. The Roman numeral system was used for trade and they did not need to represent zero with a special symbol. They used a counting board for computations and their numerals were used only for writing down the results. This does not mean they did not understand nothingness. They had a word to mean nothing but no symbol.

Super Zero!

Why do we care about zero? Zero can be used as a placeholder, with no value on its own, or as a mathematical number. For example, when we name a year, such as 2019, each numeral has its own well-defined place. We call the zero a placeholder, as it tells us that there are zero 100s. We can represent our system, in base 10, with columns as seen below:

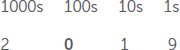
That 0 keeps the 1s on either side “in place” so we know their value. Take that placeholder away, and it is no longer clear what number we mean.

Zero can be more than a placeholder. Zero also marks the dividing point between positive numbers and negative numbers. If we count backwards with whole numbers, we reach zero. Similarly, if we count forward with negative numbers, we also arrive at 0.

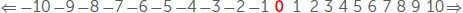
As long as you only want to count and measure, you can do it without zero. But with no zero, advanced mathematics would be impossible: no algebra, no calculus. And we would not have computers, because computers use a binary, or base 2 system, meaning that information is recorded and read as a series of 0s and 1s.

Who Invented Zero?

Arabs in the Middle Ages—centuries after the greatest age of Greek mathematics—were both remarkable mathematicians and important transmitters of ancient knowledge, including mathematics. Muhammad ibn Musa al-Khwarizmi was a famous Persian mathematician, astronomer, and geographer who contributed much to our modern understanding of mathematics, especially in the areas of algebra and trigonometry. His name—Al-Khwarizmi—eventually became Algorithmi when translated into Latin. From that Latinized version of his name, we got the word algorithm, which means the set of rules we follow when we do calculations. In the early ninth century CE, Al-Khwarizmi was head astronomer and librarian in the famous House of Wisdom in Baghdad, where he studied scientific and mathematical manuscripts, including those of the ancient Greeks and Hindus.

In Al’Khwarizmi on the Hindu Art of Reckoning, he describes a Hindu, or Indian, number system, based on 10 numerals: 1–9, and 0. He gives credit for this zero, saying that he had discovered it when he translated the mathematical works of the seventh century CE Indian scholar Brahmabgupta. This useful system was soon adopted by the Arab world.

Zero Travels a Long Road to Europe

Europeans in the Middle Ages were still conducting business using Roman numerals. But trade routes did more than move silks and spices from the East to the West—they also moved knowledge. Fibonacci, the son of an Italian merchant, often traveled for his father’s business. In North Africa he discovered that Arab traders were using an accounting system based on 10 numbers, 1–9 + 0. He quickly understood that this system could improve bookkeeping and accounting in Europe. In 1202, he published a book called Liber Abaci, which spread the idea of this new number system that had a zero “to keep the rows.” The book talked about the system’s practical applications: how to convert one currency to another, calculations of profits and losses, and other important business needs [2].

The Search Moves to India and Cambodia

Georges Cœdès was in his early 20s when he visited the Near East Collection at the Louvre, the famous museum in Paris near where he lived. He was intrigued an ancient Babylonian inscription in a display. This early experience led him to study ancient languages and to spend his life uncovering ancient mysteries contained in inscriptions from Southeast Asia.

Cœdès had an intriguing theory. He believed that numerals had originated in civilizations throughout Asia that shared a common culture based in the religions of Buddhism or Hinduism. Other scholars at the time assumed that numbers had to have come from Greece or Arabia, but Cœdès felt that this belief failed to value the intellectual developments of the East. At this point, Cœdès had no proof for his theory. Then, in the course of his work, he came across an untranslated inscription found on a stone that he called K-127, from an ancient temple at Sambor on Mekong in Cambodia. Translating the writing, he was stunned to discover that it contained the elusive zero that he had hoped to find! (Figures 1, 2).

The inscription describes a merchant’s transactions and includes a date with a zero—a placeholding zero—represented as a small dot! Whoever carved the inscription conveniently added the date: 605 of the çaka era. Converting the çaka date to our own calendar system was not difficult. Cœdès knew that the first king of the çaka era began his rule in the year 78, so by adding 78 to the 605 on the stone he knew that the inscription had been made in the year 683 CE. Cœdès had his proof, which he published in a 1931 scientific paper [3]. This proved that zero had originated in the East, because this zero found in Cambodia was carved before the work of Arab mathematicians. This early finding proved that our written digits and the zero had an Eastern, Asian origin [4].

Another Twist to Our Number Theory

About 40 years before Cœdès translated K-127, a manuscript written on birch bark, called the Bakhshali Manuscript, was found in Bakhshali, in what is now Pakistan. This text contained an ancient zero represented by a small circle. The age of this zero was not known, but some experts believed it was very old. Unlike K-127, this manuscript did not conveniently include a date in the text, so it was hard to determine when it was written. Also, scholars believed that parts of the manuscript had been written at different times.

Today, the Bakhshali is in the Bodleian Library of Oxford University. In 2017 [5], the Bodleian permitted a small piece of the bark material to be removed for radiocarbon dating. Results indicated that the portion containing the zero dates from the third or fourth century. If this is correct, the Bakhshali manuscript is older than K-127, and older than any inscription containing zero yet discovered. Some experts are not convinced. Their argument is that the section removed for testing did not contain any writing—and because the pages are believed to have been written at different times, this presents a problem. Scientists are hoping the Bodleian Library will conduct further tests on other parts of the manuscript. Many questions remain—how accurate is the method of dating used on the manuscript? Will other, older zeros be discovered? And finally, how did the idea of zero move from India to Cambodia and Indonesia and then spread to the rest of the world? What we do know is that the zero we use today was born in Southern Asia! We hope future historians of mathematics will fill in more pieces of this intriguing puzzle.

End of Story?

So why did an Indians civilization invent zero? While the Greeks believed zero was nothing, nothingness was very important in certain religions of the East, including Buddhism and Hinduism. Perhaps Indian religion and philosophy hold a clue. In any event, mathematics—and the numbers—have many questions just waiting for you to explore.

Glossary

Base 60 (Sexagesimal) System: ↑ An ancient number system that uses sixty as its base. This system was used by the ancient Sumerians in the third millennium BCE, was passed down to the ancient Babylonians, and is still used today for measuring time, angles, and geographic coordinates.

Base 10 (Decimal) System: ↑ Our current number system is a base-10 system, which has 10 digits and uses place value and a decimal point to separate whole numbers from decimal fractions.

Placeholder: ↑ A number with no value on its own, used in decimals and number lines to show the value of other numbers.

Whole Numbers: ↑ Non-decimal or non-fraction numbers, such as 1, 2, 3 onwards.

Base 2 (Binary) System: ↑ A system in which information can be expressed by combinations of the digits 0 and 1.

Middle Ages: ↑ The time period in European history from the fall of the Roman Empire in the West (around 1100) to the fall of Constantinople (1453).

Radiocarbon Dating: ↑ A scientific method used to determine the age of an object based on a radioactive isotope of carbon.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Footnotes

1. ↑ Ifrah [1] is a good introduction to the full history of numbers from “prehistory to the computer”!

2. ↑ http://www.amathsdictionaryforkids.com/qr/b/base10system.html.