תַקצִיר
בעוד שהבּבלים, היוונים והרומאים היו מסוגלים לבצע חישובים מתוחכמים להפליא, ההתפתחות המתמטית הייתה מוגבלת עד להכרת האפס האמיתי. במאמר זה אנו נסביר מדוע האפס הוא התפתחות חשובה כל כך. ננסה לענות על השאלה: מהיכן הגיע האפס, ובן כמה הרעיון של אפס? ישנן ראיות חזקות לכך שהאפס הוא התפתחות מזרחית שהגיע למערב מהודו או מציוויליזציה עם שורשים בהודו, כמו למשל קמבודיה. משמעות הדבר היא שהאפס הוא לא המצאה יוונית או מערבית, כפי שמשכילים נהגו לחשוב. מתמטיקה היא מסתורין נפלא – הרבה שאלות נותרו לגבי כיצד ומדוע האפס התפתח במערב, וכיצד הוא הגיע לאירופה.
האפס – גיבור אמיתי!
דמיינו לרגע כיצד החיים שלכם היו נראים ללא העיגול הקטן הזה שאנו משתמשים בו לייצוג האפס!
בעוד שבדרך כלל אנו לוקחים את האפס כמובן מאליו, זו המצאה חדשה יחסית. לבבלים ולרומאים לא הייתה דרך לייצג את האפס עם סמל מובחן; וגם לא ליוונים, שלא חשבו ש“כלום” הוא מספר. בני המאיה שחיו במרכז אמריקה השתמשו ברעיון של אפס [1]1 במערכת לוח השנה שלהם, אולם מאחר שהם היו מבודדים מאנשים אחרים, האפס שלהם לא הגיע מעבר לציוויליזציה שלהם. כדי למצוא מקור לאפס, עלינו לחפש במקום אחר.
בואו נסתכל על מספרים ששימשו בבבל העתיקה, שם הייתה מערכת מתמטיקה מתוחכמת לפני יותר מ-5,000 שנים. המערכת הזו התפתחה ושוכללה ממערכות עתיקות עוד יותר של כתיבת מספרים וביצוע חישובים! אנו יודעים על המערכת הבבלית מאחר שהם כתבו על לוחות חימר ששרדו עד היום. הבבלים היו מתמטיקאים ואסטרונומים טובים, שהשתמשו במערכת בסיס 60 מורכבת, ולא במערכת בסיס 10i כמו שלנו2. במתמטיקה המודרנית, אנו עדיין משתמשים בבסיס 60 לתפקודים מסוימים. לדוגמה, חשבו על האופן שבו אנו מודדים זמן: 60 שניות הן דקה אחת, 60 דקות הן שעה אחת. הבבלים, כמונו, השתמשו במיקומים (כמו אלה שבבסיס 10 שלנו, שמציינים אחדוֹת, עשרות, מאות, אלפים וכן הלאה) כדי לייצג מספרים. אולם שימוש במערכת בסיס 60 משמעותו שהחישובים והמעקב אחרי מיקומים היו מורכבים יותר. במערכת בסיס 60, מיקומים ייצגו 6 אחדות, שישים, שש מאות, שישה אלפים, וכולי. דמיינו שאתם מנסים לעקוב אחרי מיקומים בלי שיש לכם את סמל האפס שמסמן רווח. סמל האפס הקטן הזה שימושי ביותר. הבבלים בסופו של דבר החלו לסמן את הטור הריק באמצעות רווח, אולם חשבו עד כמה קל לפספס רווח בטורים של מספרים. עם המערכת המורכבת שלהם, הבבלים היו צריכים להסתמך על ההקשר כדי להבין את משמעות המספר. כדוגמה לשימוש בהקשר, אם מישהו אומר לכם שמשהו עולה ארבע וחמישים, אתם תניחו שמדובר ב-4.50 שקלים, אם אתם חושבים על הזמנת גלידה, ולא 450 שקלים, מה שעשוי להיות הגיוני אם הייתם קונים כרטיס טיסה.
היוונים הכירו את האפס כרעיון, אולם לא חשבו עליו כמספר עם אותה השימושיות במתמטיקה כמו הספרות 9-1. לפי אריסטו, לא היה אפשרי לחלק ב-0 ולקבל תוצאה משמעותית, אז המערכת היוונית הייתה מבוססת על 9 מספרים – בלי 0.
הרומאים לא השתמשו במספרים לחישובים, לכן לא היה להם צורך במספר אפס כשומר מקום או כמייצב עמודה ריקה. מערכת המספרים הרומית שימשה למסחר, והם לא היו צריכים לייצר את המספר אפס באמצעות סמל מיוחד. הם השתמשו בלוח ספירה עבור חישובים, והמספרים שלהם שימשו רק לכתיבת תוצאות. זה לא אומר שהם לא הבינו את מושג הכלום. הייתה להם מילה שמשמעותה כלום, אולם לא היה לה סמל.
סוּפֶּר אפס!
מדוע אכפת לנו מהאפס? אפס יכול לשמש כשומר מקום, ללא ערכים משל עצמו, או כמספר מתמטי. לדוגמה, כשאנו משׁיימים שנים, כמו למשל 2019, לכל מספר יש את המקום המוגדר שלו. אנו קוראים לאפס שומר מקום מאחר שהוא אומר לנו כמה שנים יש. אנו יכולים לייצג את המערכת שלנו, בבסיס 10, באמצעות עמודות כפי שאפשר לראות כאן:
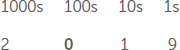
ה-0 שומר על כל ספרת 1 במקום שלה, כך שנדע מה הערך שלה (1, 10, 100, 1,000). אם תמחקו את שומר המקום הזה, כבר לא יהיה ברור לאיזה מספר מתכוונים.
אפס יכול להיות יותר מאשר רק שומר מקום. אפס גם מסמל את נקודת החלוקה בין מספרים חיוביים ושליליים. אם אנו סופרים לאחור באמצעות מספרים שלמים, אנו מגיעים לאפס. באופן דומה, אם אנו סופרים קדימה עם מספרים שליליים, אנו גם מגיעים ל-0.
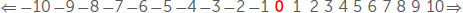
כל עוד אתם רק רוצים לספור ולמדוד, אתם יכולים לעשות את זה בלי אפס. אולם בלי אפס, מתמטיקה מתקדמת לא תהיה אפשרית: אין אלגברה, אין חשבון אִינְפִינִיטֶסִימָלִי, ולא היו לנו מחשבים, מאחר שמחשבים משתמשים בבסיס בינרי, או מערכת בסיס 2, מה שאומר שהמידע נרשם ונקרא כסדרה של הספרות 0 ו-1.
מי המציא את האפס?
ערבים בימי הביניים – מאות רבות אחרי העידן המתקדם ביותר של מתמטיקה יוונית – היו גם מתמטיקאים יוצאי דופן וגם מעבירים חשובים של ידע עתיק, כולל מתמטיקה. מוחמד איבן מוסא אל-קווריזמי היה מתמטיקאי פרסי ידוע, אסטרונום וגיאוגרף אשר תרם רבות להבנה המודרנית שלנו של מתמטיקה, במיוחד לתחומים של אלגברה וטריגונומטריה. שמו – אל-קווריזמי – בסופו של דבר נהפך לאלגוריתמי כשהוא תורגם ללטינית. מהגרסה הלטינית של השם שלו אנו מקבלים את המילה אלגוריתם, שמשמעותה סֶט של חוקים שאנו עוקבים אחריהם כשאנו מבצעים חישובים. בתחילת המאה התשיעית אחרי הספירה, אל-קווריזמי היה אסטרונום מוביל וספרן בבית החוכמה המפורסם בבגדד, שם הוא חקר כתבי יד מדעיים ומתמטיים, כולל אלה של היוונים וההודים הקדומים.
בכתבו Al’Khwarizmi on the Hindu Art of Reckoning, הוא תיאר מערכת מספרים הודית או אינדיאנית שמבוססת על 10 מספרים: 9-1, ו-0. הוא נותן קרדיט למספר אפס, ואומר שהוא גילה אותו כשהוא תרגם את העבודות המתמטיות של משכיל הודי מהמאה השביעית בשם ברהמהבגופטה. המערכת השימושית הזו אומצה במהרה על-ידי העולם הערבי.
האפס עושה דרך ארוכה לאירופה
אירופאים בימי הביניים עדיין קיימו עסקים באמצעות מספרים רומיים. אולם דרכי מסחר עשו יותר משינוע של משי ותבלינים מהמזרח למערב – הם גם שינעו יֶדַע. פיבונאצ’י, בנו של סוחר איטלקי, לעיתים קרובות טייל עבור העסק של אביו. בצפון אפריקה, הוא גילה שהסוחרים הערבים השתמשו במערכת ספירה שמבוססת על 10 מספרים, 1-9 + 0. הוא הבין במהרה שהמערכת הזו תשפר את ראיית החשבון ואת החשבונאות באירופה. ב-1202 הוא פרסם ספר שנקרא Liber Abaci, שהפיץ את הרעיון של מערכת המספרים החדשה הזו שהיה בה 0 כדי “לשמור על השורות”. הספר דיבר על היישומים השימושיים של המערכת הזו: כיצד להמיר מטבע אחד לאחר, חישובים של רווחים והפסדים וצרכים עסקיים חשובים אחרים [2].
החיפוש עובר להודו ולקמבודיה
ג’ורג’ס קודס היה בשנות ה-20 המוקדמות שלו כשהוא ביקר באוסף ’המזרח הקרוב’ במוזיאון הלובר, המוזיאון המפורסם בפריז ליד מקום מגוריו. הוא התעניין בכתובת הבבלית העתיקה בתצוגה. החוויה מוקדמת הזו הובילה אותו לחקור שפות עתיקות, ולבלות את חייו בחשיפת תעלומות שנכללו בכתובות מדרום-מזרח אסיה.
לקודס הייתה תיאוריה מסקרנת. הוא האמין שמספרים הגיעו מציוויליזציות דרך אסיה, שחלקוּ תרבות משותפת שהתבססה על דתות הבודהיזם וההינדואיזם. משכילים אחרים באותו הזמן הניחו שמספרים הגיעו מיוון או מערב הסעודית, אולם קודס הרגיש שהאמונה הזו כשלה בהערכת ההתפתחויות האינטלקטואליות במזרח. בנקודה הזו, לקודס לא הייתה הוכחה לתיאוריה שלו. לאחר מכן, במהלך עבודתו, הוא נתקל בכתובת לא מתורגמת שנמצאה על אבן שהוא קרא לה K-127, ממקדש עתיק בסאמבור שבמקונג, קמבודיה. בעת תרגום הכתוב, הוא היה המום לגלות שהיא הכילה את האפס החמקמק שהוא קיווה למצוא! (איורים 1, 2).

- איור 1 - אפס בתפקיד נקודה ב-K-127.
- הגדלה של תאריך שמוצג על K-127 עם אפס שמיוצג כנקודה.

- איור 2 - העתקה לנייר של K-127 שבוצעה על-ידי המוזיאון הלאומי של קמבודיה ב-2015.
- K-127, כתובת עתיקה שנמצאה בקמבודיה עם אחד מהאפסים העתיקים ביותר שידועים.
הכתובת תיארה העברה של סחורה, וכללה תאריך עם אפס – אפס שומר מקום – שיוצג כנקודה קטנה! מי שחקק את הכתובת, הוסיף באופן נוח את התאריך: 605 של עידן çaka. המרת עידן çaka למערכת לוח השנה שלנו לא הייתה קשה. קודס ידע שהמלך הראשון בעידן çaka התחיל למלוך בשנת 78, אז על-ידי חיבור 78 ל-605 שעל האבן, הוא ידע שהכתובת נוצרה בשנת 683 אחרי הספירה. קודס מצא את ההוכחה שלו, שפורסמה בשנת 1931 בעיתון מדעי [3]. זה הוכיח שהאפס התחיל במזרח, מאחר שהאפס הזה נמצא בקמבודיה ונחקק לפני עבודתם של מתמטיקאים ערבים. הממצא המוקדם הזה הוכיח שלספרוֹת הכתובות שלנו ולאפס היה מקור מזרחי, אסיאתי [4].
תפנית נוספת בתיאוריית המספרים שלנו
כ-40 שנים לפני שקודס תרגם את K-127, כתב יד שנכתב על ידי בירץ’ בארק, שנקרא כתב יד בקשהלי, נמצא בבקשהלי, שכיום נמצאת בפקיסטן. הטקסט הזה הכיל אפס ישן שיוצג על-ידי עיגול קטן. גילו של האפס הזה לא היה ידוע, אולם מומחים מסוימים מאמינים שהוא עתיק מאוד. שלא כמו K-127, כתב היד הזה לא כלל באופן נוח תאריך בתוך הטקסט, ולכן היה קשה לקבוע מתי הוא נכתב. נוסף על כך משכילים האמינו שחלקים מכתב היד נכתבו בזמנים שונים.
כיום, בקשהלי נמצא בספריית הבודליאנה באוניברסיטת אוקספורד. בשנת 2017 [5], בודליאנה אישרה שפיסה קטנה מחומר כתב היד של בארק תוסר עבור תארוך פחמן 14. התוצאות הצביעו על כך שהחלק בכתב היד שהכיל את האפס מתוארך לזמן שבין המאה השלישית לרביעית. אם זה נכון, כתב היד בקשהלי עתיק יותר מ-K-127, ועתיק יותר מכל כתובת שמכילה אפס שהתגלתה עד היום. חלק מהמומחים אינם משוכנעים. הוויכוח הוא שהחלק הזה שהוסר עבור בדיקה לא הכיל כתב – ומאחר שמאמינים שהעמודים נכתבו בזמנים שונים, זה עורר בעיה. מדענים מקווים שספריית בודליאנה תערוך מבחנים נוספים על חלקים אחרים של כתב היד. שאלות רבות נותרות – עד כמה השיטה שמשמשת לתארוך כתב היד מדויקת? האם יתגלו אפסים אחרים, עתיקים יותר? ולבסוף, כיצד הרעיון של האפס זז מהודו לקמבודיה ולאינדונזיה, ואז התפשט לשאר העולם? מה שאנו יודעים זה שהאפס שאנו משתמשים בו כיום נולד באסיה הדרומית! אנו מקווים שהיסטוריונים של המתמטיקה יחברו בעתיד עוד פיסות בפאזל המסקרן הזה.
סוף הסיפור?
אז מדוע התרבות ההודית המציאה את האפס? בעוד שיוונים האמינו שאפס הוא כלום, הכלום היה חשוב מאוד לדתות מזרחיות מסוימות, כולל בודהיזם והינדואיזם. אולי הדת והפילוסופיה ההודית מהוות רמז. בכל מקרה, מתמטיקה – ומספרים – כוללים הרבה שאלות שרק מחכות שתחקרו אותן.
מילון מונחים
מערכת בסיס 60 – סקסגסימלי [Base 60 (Sexagesimal) System]: ↑ מערכת מספרים קדומה שהשתמשה בשישים כבסיס שלה. המערכת שימשה את הסומריאנים הקדומים באלף השלישי לפני הספירה, הועברה הלאה לבבלים הקדומים, ונמצאת כיום בשימוש למדידת זמן, זוויות, וקואורדינטות גיאוגרפיות.
מערכת בסיס 10 – דצימלי [Base 10 (Decimal) System]: ↑ מערכת המספרים הנוכחית שלנו היא מערכת בסיס 10, שמכילה 10 ספרות ומשתמשת בערך מיקום ובנקודה עשרונית כדי להפריד מספרים שלמים משברים עשרוניים.
שומר מקום (Placeholder): ↑ מספר שאין לו ערך משלו, והוא משתמש במספרים דצימליים ובקווי מספרים כדי להראות את הערך של מספרים אחרים.
מספרים שלמים (Whole Numbers): ↑ מספרים לא עשרוניים, או לא שברים, כמו למשל 1, 2, 3 וכן הלאה.
מערכת בסיס 2 – בינרי [Base 2 (Binary) System]: ↑ מערכת שבה המידע יכול להיות מיוצג על-ידי שילובים של הספרות 0 ו-1.
ימי הביניים (Middle Ages): ↑ תקופת זמן בהיסטוריה האירופית מנפילתה של האימפריה הרומית במערב (בסביבות שנת 1100) עד לנפילתה של קונסטנטינופול (1453).
תארוך פחמן-14 (Radiocarbon Dating): ↑ שיטה מדעית שמשמשת לקביעת הגיל של אובייקט, בהתבסס על איזוטופ רדיואקטיבי של פחמן.
הצהרת ניגוד אינטרסים
המחברים מצהירים כי המחקר נערך בהעדר כל קשר מסחרי או פיננסי שיכול להתפרש כניגוד אינטרסים פוטנציאלי.
הערות שוליים
1. ↑ המאמר של Ifrah [1] הוא הקדמה טובה להיסטוריה המלאה של מספרים “מפרהיסטוריה למחשבים”!
2. ↑ http://www.amathsdictionaryforkids.com/qr/b/base10system.html.
מקורות
[1] ↑ Ifrah, G. 2000. The Universal History of Numbers. New York, NY: John Wiley & Sons, Inc.
[2] ↑ Walker Publishing Co. 2011. The Man of Numbers: Fibonacci’s Arithmetic Revolution. London: Walker Publishing Co.
[3] ↑ Coedès, G. 1931. A propos de l’origine des chiffres arabes. Bull. School Orient. Stud. 6:323–8.
[4] ↑ Coedès,G. 1968. The Indianized States of Southeast Asia. Honolulu, HI: University of Hawaii Press.
[5] ↑ Oxford University News. 2017. Earliest Recorded Use of Zero Is Centuries Older Than First Thought. Available online at: http://www.ox.ac.uk/news/2017-09-14-earliest-recorded-use-zero-centuries-older-first-thought
