الصفر بطل متفانٍ!

تخيل لدقيقة كيف ستكون حياتك بدون تلك النقطة الصغيرة التي نستخدمها لتمثيل الصفر!

في حين أننا نعتبر الصفر أمرًا مسلمًا به، إلا أنه اكتشاف حديث نسبيًا. إذ لم يكن لدى البابليين والرومان طريقة للتعبير عن الصفر برمز مميز؛ مثلهم في ذلك مثل اليونانيين الذين لم يكن يخطر ببالهم أن “اللا شيء” يعتبر رقمًا. أما شعب المايا الذين كانوا يعيشون في أمريكا الوسطى، فقد استخدموا فكرة الصفر [1]¹ في نظام التقويم الخاص بهم، ولكن نظرًا لانعزالهم عن الآخرين، فقد اقتصر الصفر الخاص بهم عليهم فقط ولم ينتقل خارج حضارتهم. ومن أجل العثور على مصدر اكتشاف الصفر، علينا أن نبحث في أماكن أخرى.

دعونا نلق نظرة على الأرقام المستخدمة في بابل القديمة، حيث كان هناك نظام رياضي متطور قبل أكثر من 5000 عام. وقد خضع هذا النظام للتطوير والتحسين من خلال أنظمة قديمة لكتابة الأرقام وإجراء الحسابات! يُذكر أننا نعرف الكثير عن النظام البابلي، حيث اعتادوا الكتابة على ألواح طينية لا زالت باقية إلى الآن. وقد كان البابليون علماء رياضيات وفلكيين ماهرين استخدموا نظام عد ستينيًا معقدًا، بدلًا من نظام العد العشري² الخاص بنا. في الرياضيات الحديثة، ما زلنا نستخدم نظام العد الستيني لأداء وظائف معينة. على سبيل المثال، فكر في كيفية حساب الوقت: 60 ثانية في الدقيقة، و60 دقيقة في الساعة. وقد استخدم البابليون، مثلنا، المواضع أو الخانات لتمثيل الأرقام (مثل نظام العد العشري للآحاد والعشرات والمئات والآلاف). إلا أن استخدام نظام العد الستيني يعني أن الحسابات وعملية تتبع الأماكن كانت معقدة للغاية. ففي نظام العد الستيني، تصبح المواضع هي مضاعفات الستة والستين والستمائة والستة آلاف. وتخيل أنك تحاول تتبع المواضع بدون وجود رمز للصفر لتمييز المكان. فهذا الرمز الصغير الذي يمثل الصفر مفيد للغاية. في النهاية، بدأ البابليون في تمييز الخانة الفارغة بمسافة، الأمر الذي يجعلنا نفكر في مدى سهولة ترك مساحة في خانات الأرقام. ومع نظامهم المعقد، كان على البابليين الاعتماد على السياق لفهم معنى الرقم. وكمثال على استخدام السياق، إذا أخبرك أحدهم أن شيئًا ما يكلف أربعة وخمسين، فيمكنك الاعتقاد أنهم 4.50 من الدولارات، إذا كنت تفكر في طلب آيس كريم، بدلًا من الاعتقاد أنهم 450 دولارًا، وهو الأمر الذي قد يبدو منطقيًا إذا كنت تشتري تذكرة طيران.

أما الإغريق فقد عَرَفوا الصفر باعتباره أحد المفاهيم لكنهم لم يفكروا فيه باعتباره رقمًا له نفس الفائدة في الرياضيات مثل الأرقام من 1 إلى 9. فوفقًا لأرسطو، لم يكن من الممكن القسمة على 0 والحصول على نتيجة ذات معنى، لذلك كان النظام اليوناني قائمًا على 9 أرقام - بدون الصفر.

من ناحية أخرى، لم يستخدم الرومان الأرقام في الحسابات، لذلك لم يكونوا بحاجة إلى الصفر لشغل خانة ما أو لإبقاء إحدى الخانات فارغة. استُخدم نظام الأرقام الرومانية في التجارة ولم تكن هناك حاجة لتمثيل الصفر برمز خاص. كما استخدموا لوحة عد للحسابات واستخدمت أرقامهم فقط لتدوين النتائج. وهذا لا يعني أنهم لم يفهموا معنى العدم أو اللا شيء؛ فقد كانت لديهم كلمة تعني لا شيء ولكن بدون أي رمز.

الصفر الخارق!

لماذا نولي الصفر أهمية؟ يمكن استخدام الصفر باعتباره عنصرًا نائبًا، مع عدم وجود قيمة له بمفرده، أو باعتباره عددًا رياضيًا. فعلى سبيل المثال، حين نسمي سنة ما، مثل 2019، يكون لكل رقم مكانه الخاص. ونسمي الصفر عنصرًا نائبًا، لأنه يخبرنا أنه يوجد صفر في خانة المئات. ويمكننا تمثيل نظامنا، نظام العد العشري، بالخانات على النحو الموضح أدناه:

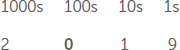
يحافظ العدد 0 على الآحاد على أحد الجانبين ”في مكانها” حتى نعرف قيمتها. وإذا مسحت هذا العنصر النائب، فلن يعد الرقم الذي نعنيه واضحًا.

قد يكون الصفر أكثر من مجرد عنصرًا نائبًا؛ فالصفر يشير أيضًا إلى النقطة الفاصلة بين الأرقام الموجبة والأرقام السالبة، فإذا قمنا بالعد تنازليًا بالأعداد الصحيحة، فسنصل إلى الصفر. وبالمثل، إذا قمنا بالعد تصاعديًا بأرقام سالبة، فإننا نصل أيضًا إلى 0.

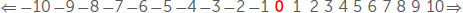
وطالما أنك تريد العد والقياس فقط، فيمكنك القيام بذلك بدون الصفر. ولكن في ظل غياب الصفر، فإن الرياضيات المتقدمة ستكون مستحيلة: فلن يكون هناك جبر، ولا حساب تفاضل وتكامل. فضلًا عن ذلك، لن يكون لدينا أجهزة كمبيوتر، لأن أجهزة الكمبيوتر تستخدم نظامًا ثنائيًا أو نظام القاعدة الثنائية، مما يعني أن المعلومات يتم تسجيلها وقراءتها على شكل سلسلة من الصفر والواحد.

من اخترع الصفر؟

كان العرب في العصور الوسطى - بعد قرون من أعظم عصر للرياضيات اليونانية - علماء رياضيات بارزين وناقلين مهمين للمعرفة القديمة، بما في ذلك الرياضيات. وقد كان محمد بن موسى الخوارزمي عالمًا فارسيًا مشهورًا في الرياضيات وعلم الفلك والجغرافيا، وقد قدم إسهامات كثيرة في فهمنا الحديث للرياضيات، خاصةً في مجالي الجبر وعلم المثلثات. وحين تُرجم اسمه - الخوارزمي - إلى اللاتينية أصبح خوارزمية. ومن تلك النسخة اللاتينية من اسمه، حصلنا على كلمة “خوارزمية” (Algorithmi)، والتي تعنى مجموعة القواعد التي نتبعها عندما نقوم بالحسابات. وفي أوائل القرن التاسع الميلادي، كان الخوارزمي كبير علماء الفلك وأمين مكتبة في بيت الحكمة الشهير في بغداد، حيث درس المخطوطات العلمية والرياضية، بما في ذلك المخطوطات اليونانية والهندوسية القديمة.

وفي كتابه: “الفن الهندوسي في الحساب” (Hindu Art of Reckoning) للخوارزمي، وصف نظام العد الهندوسي أو الهندي، استنادًا إلى 10 أعداد: من 1 إلى 9 والعدد 0. وقد أعطى الفضل لهذا الصفر، قائلًا إنه اكتشفه عندما ترجم الأعمال الرياضية للعالم الهندي Brahmabgupta من القرن السابع الميلادي. وسرعان ما تبنى العالم العربي هذا النظام المفيد.

رحلة الصفر الطويلة وصولًا إلى أوروبا!

كان الأوروبيون في العصور الوسطى لا يزالون يمارسون الأعمال التجارية باستخدام الأرقام الرومانية، لكن طرق التجارة تخطت مجرد نقل الحرير والتوابل من الشرق إلى الغرب - فقد نقلت هذه الطرق المعرفة أيضًا. كان Fibonacci، ابن أحد التجار الإيطاليين، كثير الترحال من أجل عمل والده. وفي شمال إفريقيا اكتشف أن التجار العرب يستخدمون نظام حساب قائمًا على 10 أعداد، من 1 إلى 9 + العدد 0. وسرعان ما أدرك أن هذا النظام يمكن أن يحسن من نظام إدارة الحسابات والمحاسبة في أوروبا. وفي عام 1202، نشر كتابًا بعنوان “ليبر أباتشي” (Liber Abaci)، والذي نشر فكرة هذا النظام الجديد للأعداد الذي يحتوي على العدد صفر “للحفاظ على الخانات”. كما تحدث الكتاب عن التطبيقات العملية للنظام مثل: كيفية تحويل عملة إلى أخرى، وحسابات الأرباح والخسائر، وغيرها من احتياجات العمل المهمة [2].

انتقال البحث إلى الهند وكمبوديا

كان Georges Coedès في أوائل العشرينيات من عمره عندما زار مجموعة الشرق القريب في متحف اللوفر، المتحف الشهير في باريس بالقرب من محل سكنه، وقد كان مفتونًا بأحد النقوش البابلية القديمة المعروضة. حيث قادته هذه التجربة المبكرة إلى دراسة اللغات القديمة وقضاء حياته في الكشف عن الألغاز القديمة الموجودة في النقوش من جنوب شرق آسيا.

كان لدى Coedès نظرية مثيرة للاهتمام، حيث كان يعتقد أن الأرقام نشأت في الحضارات الموجودة في جميع أنحاء قارة آسيا التي تتشارك ثقافة مشتركة تستند إلى ديانات البوذية أو الهندوسية. بينما افترض علماء آخرون في تلك الفترة أن الأعداد كان يجب أن تأتي من اليونان أو الجزيرة العربية، لكن شعر Coedès أن هذا الرأي قد فشل في تقدير التطورات الفكرية في الشرق. وفي هذه المرحلة، لم يكن لدى Coedès أي دليل على نظريته. وفيما بعد، أثناء عمله، صادف نقشًا غير مترجم عُثر عليه على حجر أسماه K-127، من معبد قديم في سامبور على نهر ميكونغ في كمبوديا. وعند ترجمة الكتابة، صُدم عندما اكتشف أنها تحتوي على الصفر صعب المنال الذي كان يأمل في العثور عليه! (الشكلين 1 و2).

كان النقش يصف معاملات أحد التجار ويتضمن تاريخًا به العدد صفر - كنقطة تعويضية - في شكل نقطة صغيرة للغاية! أيًا كان من نحت النقش، فقد أضاف التاريخ بصورة ملائمة: 605 من عصر شاكا. لم يكن تحويل تاريخ الشاكا إلى نظام التقويم الخاص بنا أمرًا صعبًا، فقد عرف Coedès أن أول ملك من عصر الشاكا قد بدأ حكمه في عام 78، لذلك بإضافة 78 إلى 605 على الحجر، عرف أن النقش قد تم في عام 683 م. كان لدى Coedès دليله الذي نشره في ورقة علمية عام 1931 [3]. أثبت هذا أن الصفر قد نشأ في الشرق، لأن هذا الصفر الموجود في كمبوديا تم نحته قبل عمل علماء الرياضيات العرب. وأثبت هذا الاكتشاف المبكر أن الأرقام المكتوبة والصفر من أصل آسيوي شرقي [4].

جدل آخر في نظرية الأعداد الخاصة بنا

تم العثور على مخطوطة مكتوبة على لحاء شجرة البتولا، سُميت مخطوطة بخشالي، قبل ما يقرب من 40 عامًا من ترجمة Coedès لحجر K-127، في بخشالي، وهي الآن باكستان. احتوى هذا النص على صفر قديم في صورة دائرة صغيرة. لم يتم التعرّف على عمر هذا الصفر، لكن بعض الخبراء اعتقدوا أنه كان قديمًا للغاية. وعلى النقيض من حجر K127، لم تتضمن هذه المخطوطة تاريخًا ملائمًا في النص، لذا كان من الصعب تحديد وقت كتابتها. فضلًا عن ذلك، اعتقد العلماء أنه تمت كتابة أجزاء من المخطوطة في أوقات مختلفة.

وفي وقتنا الحالي، تتواجد مخطوطة بخشالي في مكتبة بودلي بجامعة أوكسفورد. وفي عام 2017 [5]، سمحت مكتبة بودلي بإزالة جزء من مادة اللحاء من أجل إجراء علمية التأريخ باستخدام الكربون المشع. وأشارت النتائج إلى أن الجزء الذي يحتوي على الصفر يعود إلى القرن الثالث أو الرابع الميلادي. إذا كان ذلك صحيحًا، فإن مخطوطة بخشالي أقدم من الحجر K-127، وأقدم من أي نقش يحتوي على صفر تم اكتشافه حتى الآن. لم يقتنع بعض العلماء، وكانت حجتهم هي أن القسم الذي تمت إزالته لم يحتو على أي كتابة، ولأنهم يعتقدون أنه تمت كتابة الصفحات في أوقات مختلفة، ويمثل ذلك مشكلة. يأمل العلماء أن تجري مكتبة بودلي المزيد من الاختبارات على أجزاء أخرى بالمخطوطة. باتت هناك العديد من الأسئلة المطروحة؛ من ضمنها، ما مدى دقة أسلوب التأريخ المتبع في المخطوطة؟ هل سيتم اكتشاف أصفار أخرى أقدم؟ وأخيرًا، كيف انتقلت فكرة الصفر من الهند إلى كمبوديا وإندونيسيا ومن ثم الانتشار إلى بقية أنحاء العالم؟ ما نعرفه هو أن الصفر الذي نستخدمه اليوم ظهر في جنوب آسيا! ونأمل أن يجد مؤرخو الرياضيات في المستقبل حلًا لهذا اللغز المثير للجدل.

هل هذه نهاية القصة؟

السؤال المطروح هنا هو لماذا اخترعت الحضارة الهندية الصفر؟ فبينما اعتقد اليونانيون أن الصفر لا يعني شيئًا، كان اللا شيء من أهم المفاهيم في بعض الديانات بالشرق، بما في ذلك البوذية والهندوسية. ربما تحمل الديانة والفلسفة الهندية دليلًا. على أي حال، تتضمن الرياضيات، والأرقام، العديد من الأسئلة التي تنتظرك لاستكشافها.

مسرد للمصطلحات

نظام العد الستيني (النظام الستيني) (Base 60 (sexagesimal) system): ↑ هو نظام عد قديم يستخدم الرقم 60 كأساس له. وقد استُخدم هذا النظام من قبل السومريين القدماء في الألفية الثالثة قبل الميلاد، ونُقل إلى البابليين القدماء، ولا يزال يستخدم حتى اليوم لقياس الوقت والزوايا والإحداثيات الجغرافية.

نظام العد العشري (النظام العشري) (Base 10 (decimal) system): ↑ إن نظام العد الحالي لدينا هو نظام العد العشري، والذي يتكون من 10 أعداد ويستخدم القيمة المكانية والفاصلة العشرية لفصل الأعداد الصحيحة عن الكسور العشرية.

العنصر النائب (Placeholder): ↑ هو عدد ليس له قيمة في حد ذاته، ويستخدم في الكسور العشرية وخطوط الأرقام لإظهار قيمة الأعداد الأخرى.

الأعداد الصحيحة (Whole numbers): ↑ هي أرقام غير عشرية أو غير كسرية، مثل 1 و2 و3 وما إلى ذلك.

نظام القاعدة الثنائية (النظام الثنائي) (Base 2 (binary) system): ↑ هو نظام يمكن من خلاله التعبير عن المعلومات من خلال مجموعات من العددين: 0 و 1.

العصور الوسطى (Middle ages): ↑ الفترة الزمنية في التاريخ الأوروبي بداية من سقوط الإمبراطورية الرومانية في الغرب (في عام 1100 تقريبًا) وحتى سقوط القسطنطينية (عام 1453).

التأريخ باستخدام الكربون المشع (Radiocarbon dating): ↑ أسلوب علمي يُستخدم لتحديد عمر شيء ما استنادًا إلى أحد النظائر المشعة للكربون.

إقرار تضارب المصالح

يعلن المؤلفون أن البحث قد أُجري في غياب أي علاقات تجارية أو مالية يمكن تفسيرها على أنها تضارب محتمل في المصالح.

الحواشي

1. ↑ "إفراح" [1] (Ifrah) هو مقدمة جيدة للتاريخ الكامل للأعداد من "عصور ما قبل التاريخ حتى عصر الحاسب الآلي"!

2. ↑ http://www.amathsdictionaryforkids.com/qr/b/base10system.html.