Abstract
How do we determine the important characters in a movie like Frozen? We can watch it, of course, but there are also other ways—using mathematics and computers—to see who is important in the social network of a story. The idea is to compute numbers called centralities, which are ways of measuring who is important in social networks. In this paper, we talk about how different types of centralities measure importance in different ways. We also discuss how people use centralities to study many kinds of networks, not just social ones. Scientists are now developing centrality measures that also consider changes over time and different types of relationships.
The Movie Frozen and Social Networks
Have you seen the movie Frozen? It tells the story of two orphaned sisters, Elsa and Anna, who are princesses of the kingdom of Arendelle. Elsa has a magical power that allows her to create snow and ice, but this magic is dangerous to her and the people around her. To protect Anna, Elsa has been avoiding her since they were very young. At Elsa’s twenty-first birthday, she is crowned queen of Arendelle. At the party to celebrate her coronation, she loses control of her magic, casting Arendelle into a spell of eternal winter. Elsa gets very upset and leaves Arendelle. Anna sets off on a quest to bring back her sister and end the spell of winter. Along the way, she meets many memorable characters, like the ice harvester Kristoff, his troll friends, and of course the snowman Olaf. Anna has also been affected by Elsa’s magic and is cursed to gradually freeze to ice, so it is really important for Anna and all of Arendelle to break the spell.
In Frozen, many of the characters know each other, either before the story starts or after they meet during the movie. Elsa (of course) knows her sister Anna, who gets to know Kristoff, who knows the trolls. A collection of people who know each other, in combination with the relationships between those people, is called a social network. Social networks are important. For example, they help spread knowledge, because people tell each other things when they talk to each other or message each other. In Frozen, for example, Anna learns through a social network that her spell can be cured only by an act of true love. She learns this from the trolls, who she met through Kristoff.
Basic Ideas of Centrality Measures
Social networks can tell us something about the people in them. When somebody is in a difficult situation, they can use a little help from their friends. Who has the most friends in Frozen? That is difficult to tell just from watching the movie, but we can study another kind of social network—the network of who talks to whom. This network, which we show in Figure 1, is not exactly the same as a friendship network, but it is much easier to accurately determine who talks to whom in the movie than it is to decide exactly who is friends with each other and how strong those friendships are. In this network of conversations, Anna speaks to nine people, so we will suppose that she has nine friends. Mathematicians say that Anna is a node in this network, that she has a degree of nine, and that those nine friends are her neighbors. Similarly, Elsa has a degree of eight, because she has eight friends; and Kristoff has a degree of six. Calculating somebody’s degree is one way to measure their importance, but there are also many other ways.
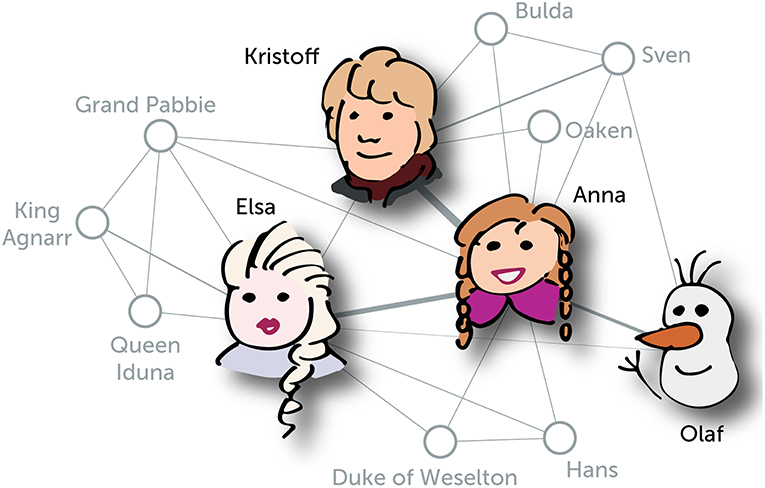
- Figure 1 - A network of the main characters of Frozen.
- This network shows who talks to whom in the movie. The more two characters say to each other, the thicker the line between them. We highlight particularly important characters in black. Each character, such as Olaf, is a “node” in the network. Olaf talks to three characters—Anna, Elsa, and Sven—in this network, so we say that he has a “degree” of three. Anna, Elsa, and Sven are Olaf’s “neighbors” in the network.
Take a close look at Figure 1. Can we figure out who is the most important character in Frozen from looking at the network in this picture? Important people often have many friends. Moreover, the friends of important people are often also important people themselves. To measure this with a number, we start by assuming at first that all characters (that is, nodes) are equally important, with an initial value of 1. We then update the importance (called centrality by people who study networks) of everyone by summing the importances of the characters to whom they are connected (in other words, their neighbors). After doing this once, the initial result is equal to the degree—that is, to the number of friends of each node. We divide these numbers by the sum of the importances of all nodes (this keeps the numbers from getting too large) to get a new set of importances. As we repeat this over and over again, replacing each node’s importance by the sum of its neighbors’ importances and dividing the results by the sum of all importances in the network, the importances eventually stop changing. Please try this yourself using Figure 2 as a worksheet; for small networks, the numbers usually stop changing quickly. The numbers that we get at the end of the calculation are called eigenvector centralities, a fancy name for the particular type of importance that we are calculating. For the network in Figure 1, if we take into account how often the characters talk to each other, Anna has the largest value, with 0.295; Kristoff comes in second, with 0.210; and Elsa comes in third, with 0.151. According to these numbers, Anna is still the most important character, but now Kristoff is ranked above Elsa. If we ignore how often characters talk to each other, the numbers change a bit: Anna is still first, with 0.146; Elsa is second, with 0.132; and Kristoff is now third, with 0.112.
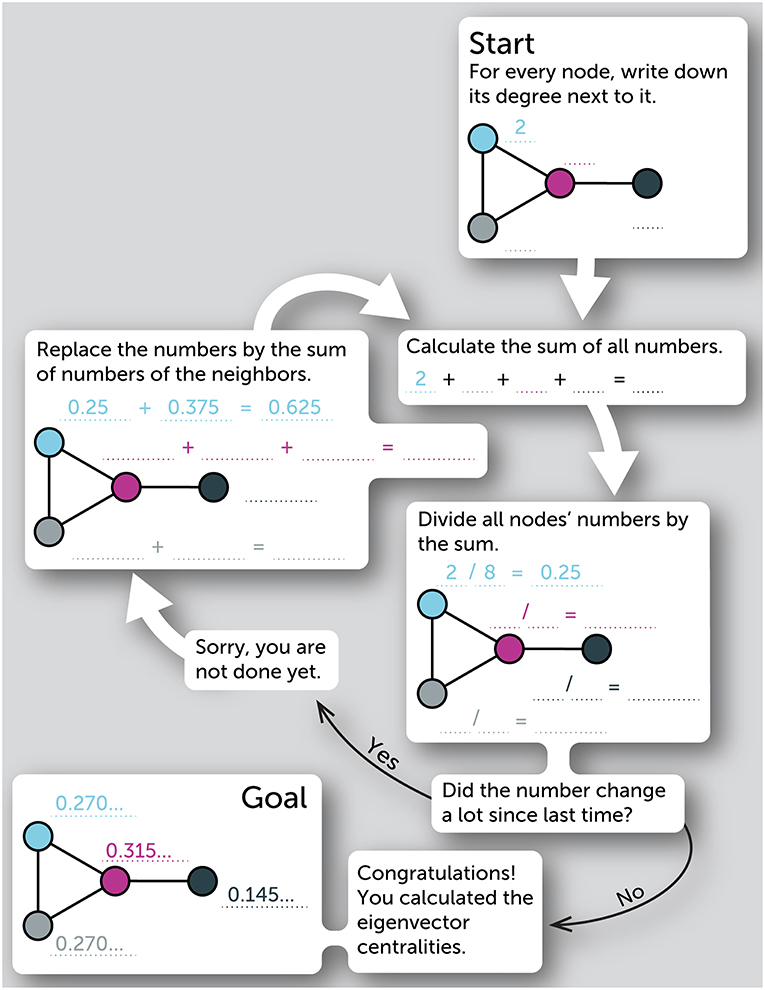
- Figure 2 - A step-by-step procedure for calculating the eigenvector centralities of the nodes in a network.
- We illustrate this procedure with a simple network. We can use it as one way to measure the importances of different characters in the movie Frozen.
At this point, you may be wondering why anybody bothers calculating numbers like eigenvector centrality to measure importance. It is clear from watching Frozen that most things happen because of Elsa’s magic, so perhaps she should be the most important character? However, take another look at the network in Figure 1: it is a network of who talks to whom, not of who performs what action that causes what major event. The network in Figure 1 tells us about who is important for the storytelling in the movie Frozen, rather than about who is important for causing the events themselves in Arendelle.
We can do a similar calculation for a narrative network, which is a network of which events cause which other events [1]. In this case, it is much more difficult to construct the network. Figure 3 is an attempt to start making such a network; maybe you will be able to complete it? In such a network, the events caused by Elsa may have really large degrees and eigenvector centralities. This means that, although Anna is most important character for telling the story of Frozen, it is instead Elsa who is most important for the events that make up the story.
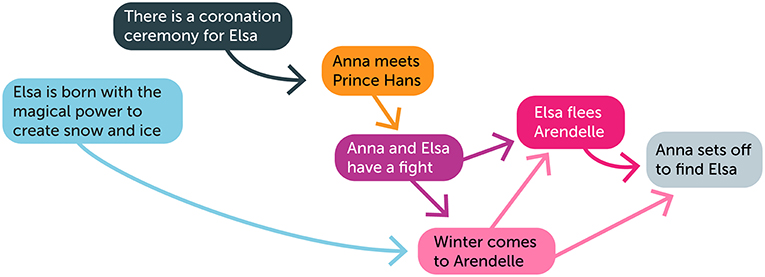
- Figure 3 - A simple but incomplete narrative network of events near the beginning of Frozen.
Networks Are Everywhere
Now that we have illustrated the idea of calculating numbers like centralities, let us step back a bit. Why should we care about these social networks and calculations? The reason is that networks are everywhere in our everyday lives, and learning about networks helps us understand a wide variety of different things [2, 3]. We will give a few examples.
One really important example of a network is the Internet. The Internet is a huge, worldwide network of computers, tablets, phones, and other devices that are interconnected by wires and wireless connections. We can think of the Internet as a social network of computers. Each computer has “friends” (other computers that are connected to it), and those friends are gateways to different parts of the network, like in the social network of Frozen characters. When you send a text message from a phone, a tablet, or a computer, it is passed on to one of its friends, to a friend of its friends, and so on, until the message eventually reaches the recipient (your friend). Knowing the properties of this gigantic network of computers is important for many practical reasons. For instance, engineers want to know which devices have greater importance (centrality) and how many steps on average are necessary to go from one device to another. In a large network like the Internet, are there a lot of steps or are there very few of them [3]?
Other examples of networks are ecological interactions in nature. Biological species interact with each other in many different ways. One of the most important interactions is who eats whom, which is called “predation.” We can pick one species (a frog, for example) and make a list of other species that eat it (like snakes and racoons) and that are eaten by it (like insects and worms). If we also make these lists for each of the species, we eventually get a large set of relationships (called a “food web”), illustrating predation relationships between many species. This is rather different from the friendships and conversations that we discussed earlier, but we can learn a lot about ecology by studying this kind of network. For example, the centrality of a species may indicate how much ecological damage would result if that species becomes extinct.
These examples illustrate the power of mathematical representations like networks. We can use the same mathematical tools to study lots of different networks, even though the real components of the network—like characters, computers, or biological species—can be very different. There are many other examples of networks in addition to those that we discussed here. Can you think of any?
What Else Can We Study About Networks?
In the examples of networks that we discussed above, we did not let the networks change, even though people make new friends all of the time, like when they go to a new school. We also did not distinguish between different types of relationships. In Frozen, for example, Elsa and Anna are sisters, but Anna and Olaf are friends.
Nowadays, scientists are actively researching ways to extend calculations to more complicated situations, such as networks in which nodes and connections are added, modified, or removed over the course of time [4]. Because the network of who talks to whom in Frozen develops over time with the flow of the story, it is desirable to measure important characters in ways that allow importances to change over time. Another prominent feature of social networks is that there are many types of relationships at once, not just friendships; and researchers are actively developing ways of measuring important nodes in a way that combines multiple relationships. This is helpful not just for social networks, but also for other kinds of networks. In nature, for instance, animals do not just eat each other; they also interact with each other in other ways, and the complex social structures of animals depend on these diverse relationships [5].
The study of networks is an exciting area of research that links ideas from mathematics, social science, physics, computer science, ecology, and many other subjects. One of the major problems in network analysis is determining the best ways to measure the importance of people, animals, and other entities. Through our illustration with the story of Frozen, we have given you a window into this exciting area of study.
Glossary
Network: ↑ A collection of nodes and the connections between nodes.
Node: ↑ The things in a network that are connected to other things. For instance, in the Frozen social network, the characters in the movie are the nodes.
Degree: ↑ The total number of neighbors of a node.
Neighbors: ↑ The nodes to which a node is connected.
Centrality: ↑ A number that expresses how important a node is.
Eigenvector Centrality: ↑ A type of centrality that is built on the idea that important nodes have important neighbors.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
We are grateful to Nia Chiou, Maria Chrysafis, Ana Gershenson, Anthony Jin, Veda Montgomery, Martha New, Kate Van Hooser, and Austin Wu for their very helpful comments on a draft of this paper. We also thank their parents and teachers—Lyndie Chiou, Christina Chow, Carlos Gershenson, Marlon Montgomery, Steve New, and Steve Van Hooser—for putting us in touch with them and soliciting their feedback. We thank the two reviewers and their Science Mentors for their valuable, constructive comments. Finally, we thank Susan Debad for carefully editing our manuscript to make it more accessible to our young audience.
References
[1] ↑ Bearman, P., Moody, J., and Faris, R. 2003. Networks and history. Complexity 8:61–71. doi: 10.1002/cplx.10054
[2] ↑ NetSciEd. (Eds). 2015. Network Literacy: Essential Concepts and Core Ideas. Available online at: http://tinyurl.com/networkliteracy. (Accessed 5 July, 2019).
[3] ↑ Newman, M. E. J. 2018. Networks, 2nd Edn. Oxford: Oxford University Press.
[4] ↑ Taylor, D., Myers, S. A., Clauset, A., Porter, M. A., and Mucha, P. J. 2017. Eigenvector-based centrality measures for temporal networks. Multiscale Model. Simul. 15:537–74. doi: 10.1137/16M1066142
[5] ↑ Finn, K. R., Silk, M. J., Porter, M. A., and Pinter-Wollman, N. 2019. The use of multilayer network analysis in animal behaviour. Anim. Behav. 149:7–22. doi: 10.1016/j.anbehav.2018.12.016