Abstract
Imagine that every time you experience a beautiful sunset, you post a picture of it on Instagram. Your first few photos get tons of “likes,” but then one day you post another one and it only gets “liked” by a few people—do you post a picture of the next sunset you see? Making choices and seeing what happens helps us learn things about the world around us, which influences the future choices that we make. Neuroscience researchers have developed mathematical models to explain how people learn from the good and bad outcomes of their past choices. These models are generally referred to as reinforcement learning models. In this article, we explain situations in which we might use reinforcement learning in the real world, how math equations can help us understand this process, and how researchers study the way the brain learns from experience to make good choices.
What is Reinforcement Learning?
Reinforcement learning is a process in which we use our past experiences to help us make choices that are likely to lead to good outcomes. Let us return to the example described in the article abstract, of posting sunset pictures on Instagram, and go through it in more detail. The first time you post a sunset picture, you get a ton of “likes,” which makes you really happy—the positive experience of receiving all those “likes” makes you more likely to post another picture. You post a second sunset picture and get just as many “likes”; you post a third one and the “likes” keep pouring in. One day though, you post what you think is a nice picture and receive almost no “likes.” Instead, someone writes a mean comment on your photo. Suddenly, not all your associations with posting sunset pictures are positive. You need to update what you have learned to take into account the negative experience of receiving a mean comment. The next time you have a chance to post a sunset picture, you might be a little less likely to do so.
The outcomes of our choices can be thought of as reinforcement signals. If we make a choice and experience something good—a positive reinforcement signal—we will be more likely to repeat that choice in the future. But if we make a decision and experience something bad, we might choose a different option next time. This process is called reinforcement learning.
Why Use Math Equations to Understand Learning and Decision-Making?
In general, positive experiences (like receiving lots of “likes” on social media) cause our expectation about how rewarding something will be to increase, and negative experiences (like receiving mean comments) cause our expectation about how rewarding something will be to decrease. However, this general description of the learning process does not help us make specific predictions about how much an experience will cause us to change our expectations. For example, imagine you post nine pictures that receive many “likes” and one picture that receives a nasty comment. How much will one nasty comment change your estimate of how rewarding it is to post a picture? How much less likely will you be to post similar pictures in the future? Without a mathematical equation to describe the learning process, we cannot answer these questions.
Additionally, researchers can write equations with different sections, where each section represents a different process involved in thinking or decision-making. Then, we can see what happens when we change each part of the equation to understand how different thought processes contribute to learning.
The Rescorla–Wagner Model
Over the years, researchers have come up with different math equations—or “computational models”—to explain how people learn from positive and negative experiences. One of the first of these models, which is still useful, is called the Rescorla–Wagner Model [1,2].
Researchers Robert Rescorla and Allan Wagner wanted to better understand a famous series of experiments that had been conducted by another researcher, Ivan Pavlov. In these experiments, Pavlov repeatedly rang a bell (it actually was a different sound-making device—a metronome—but for simplicity we call it a bell), and then gave dogs food. At first, the dogs did not associate the reward of food with the sound of the bell. But Pavlov found that, after several repetitions of this procedure, the dogs would begin to salivate when they heard the sound, even if no food was given to them. These findings suggest that, over time, the dogs learned to associate the bell with the delivery of food, such that they would anticipate the food (and salivate!) whenever they heard the bell.
As mentioned earlier, however, learning is often an incremental process. That means that each time Pavlov’s dogs heard the bell and were given food, the strength with which they associated the bell with the food increased a little bit, and they became more likely to salivate at the sound of the bell.
Can we predict how strongly a dog expects food when it hears the bell? Can we know how the dog’s predictions will change after each experience? Rescorla and Wagner wanted to come up with a math equation to answer these questions. But they could not just write any equation—they needed to write one that would accurately reflect the learning process. To do so, they first needed to understand situations in which animals learned to form associations between their experiences.
Rather than experimenting with dogs, bells, and food, Rescorla and Wagner carried out most of their experiments with rats, using a sound and electric shocks. In these experiments, rats would hear a sound and then receive an electric shock. Normally, rats run around their cages. But rats do not like being shocked, so they often freeze when they think a shock is about to happen. The strength with which a rat associates a sound with a shock can be measured by how much the rat freezes when it hears the sound. For example, the very first time the rat hears the sound, the rat will not expect a shock, so it will continue to move around its cage normally. But if it hears the sound and is then shocked, the rat will begin to learn that the sound and the shock are connected. The next time it hears the sound, the rat will move less and freeze more.
Rescorla and Wagner noticed that early on, when the rats were first learning the relationship between the sound and the shock, they showed bigger changes in how often and for how long they froze. After being shocked many times, they reached a more stable pattern of behavior—they continued to freeze, but the amount that they froze only increased a little bit after each shock.
This observation—as well as many other experiments—led Rescorla and Wagner to discover that reinforcement learning is driven by surprise. In other words, animals learn more when they encounter something they do not expect. They called this type of surprise during learning “prediction error,” because it represents the extent to which an animal’s prediction about what would happen was different than what it experienced. For example, the very first time Pavlov’s dogs heard a bell, they had no reason to expect to get any food. When they received food, they experienced surprise, or a large prediction error, because the event that actually happened (food!) differed greatly from what they predicted would happen (nothing!). This prediction error then caused them to learn that they might receive food when they hear a bell. When they did receive food the next time they heard the bell, their prediction error was lower, because they were a little less surprised at the result. As they continued to hear the bell and receive food, their expectation about the bell predicting food continued to increase, but it did not increase as much as it did the first few times, when they were more surprised by the delivery of food.
We experience “prediction errors” all the time. For example, you might think that you do not like to eat broccoli. But one day, you may decide to try it, and discover that it actually tastes pretty good! In this case, your experience of eating tasty broccoli would differ from your prediction that broccoli is gross. You would experience a prediction error, and this would cause you to learn something about broccoli and change your belief about how tasty it is.
Without prediction errors, we do not learn anything through reinforcement. For example, you might love eating pizza. One day, you might stop and get pizza on your way home from school. It is delicious! In this case, your experience of eating tasty pizza did not differ from your prediction. You would not experience a prediction error and so you would not learn anything. You would continue to think pizza tasted delicious.
Rescorla and Wagner wrote a math equation to describe this learning process. Their equation states that the increase in the strength with which an animal associates something with reward (like a bell with food) is computed by taking the difference between how much reward the animal received and how much reward the animal predicted it would receive (Figure 1).
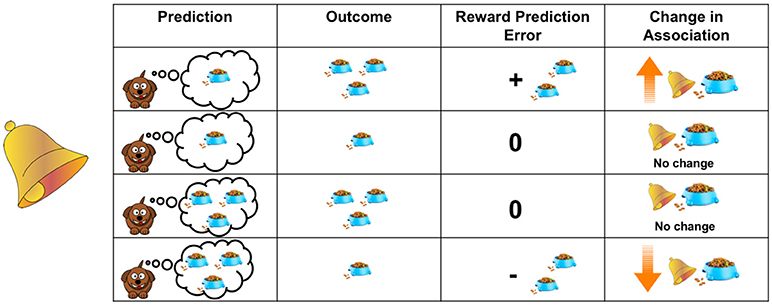
- Figure 1 - Learning is driven by prediction errors.
- The table shows different examples of how a dog’s predictions and experienced outcomes influence what it learns. The amount that a dog will increase its association between a bell and food (shown in the “Change in Association” column) is determined by the difference between how much food it receives when it hears the bell (shown in the “Outcome” column) and how much food it predicted it would receive (shown in the “Prediction” column). This difference is referred to as the “Reward Prediction Error” and is shown in that column.
This equation can tell us how strongly an animal associates two things or how much reward a certain decision, like posting a picture on Instagram, is likely to bring about.
In addition to the important prediction error term in the equation, there is also another term called the “learning rate.” The learning rate just tells us how much the animal updates its estimates after each experience and is multiplied by the prediction error. We can think of the learning rate as representing how quickly each animal learns. If an animal has a high learning rate, then it updates its estimates a lot when it experiences a prediction error. But if an animal has a lower learning rate, then it might rely to a greater extent on all of its past experiences, and only change its estimate a little bit each time it experiences a prediction error.
How Does the Brain Learn from Reinforcement?
Reinforcement learning models have been useful in helping us understand how the brain learns. The brain is made up of around 100 billion brain cells called neurons. Neurons release chemicals called neurotransmitters, which help neurons send (transmit) messages to each other. Dopamine is one important neurotransmitter in the brain. Dopamine neurons respond to the rewards we experience in our environments.
Using experiments like the ones described earlier, scientists have shown that the activity of dopamine neurons plays a key role in representing prediction errors in the brain. After learning, dopamine neurons show increased activity in response to something that predicts a reward, like a bell, before an animal even receives a reward. If an animal expects to receive a reward, but then does not, dopamine neurons will decrease their activity. In terms of the reinforcement learning model, we can think of dopamine as a prediction error signal—activity of dopamine neurons signals differences between how much reward you think you will get vs. how much reward you actually get [3]. This helps us learn from reinforcement and ultimately helps us use our previous experiences to make choices that we think will lead us to rewards (Figure 2).
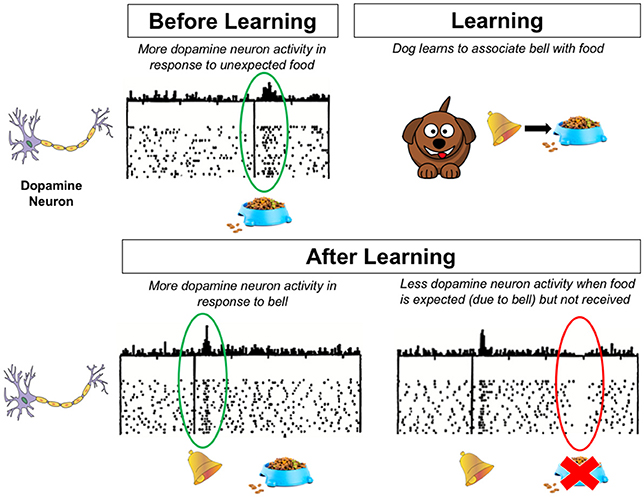
- Figure 2 - This figure shows what is happening in the dog’s brain before and after learning.
- Dopamine neurons respond to rewards and predictions about rewards. The dots represent the activity of a dopamine neuron over time. The height of the lines on top of the dots represent the number of dots directly below it, for that specific time point. Dopamine neurons respond to a reward, like food (top left). After the dog learns to associate a bell with food, dopamine neurons can respond to something that predicts a reward, like a bell (bottom left). Note that the dopamine neurons will not respond to the food itself in this case, since it is no longer surprising. However, if the predicted reward does not happen, dopamine neurons become less active (bottom right). Adapted from Schultz et al. [3].
Many different parts of the brain show patterns of activity that look similar to the prediction error signal from dopamine neurons. One such part of the brain is a group of regions located deep inside the brain known as the basal ganglia. The basal ganglia are important not just for helping us learn but also for controlling our movements and our habits. The largest part of the basal ganglia is the striatum. The striatum is a major site of dopamine release and is a central part of the brain systems that control our responses to rewards.
Many studies in animals and humans have shown that activity in the striatum is related to prediction errors and plays an important role in reinforcement learning [4]. Patterns of brain activity related to prediction errors can also be seen in the frontal cortex of the brain, an area that is involved in decision-making. The striatum and frontal cortex have many connections with each other that are thought to be critical for helping us to quickly do the calculations described by reinforcement learning equations. These connections might explain how we can quickly learn from an experience and use this knowledge to help us with our future decisions (Figure 3).
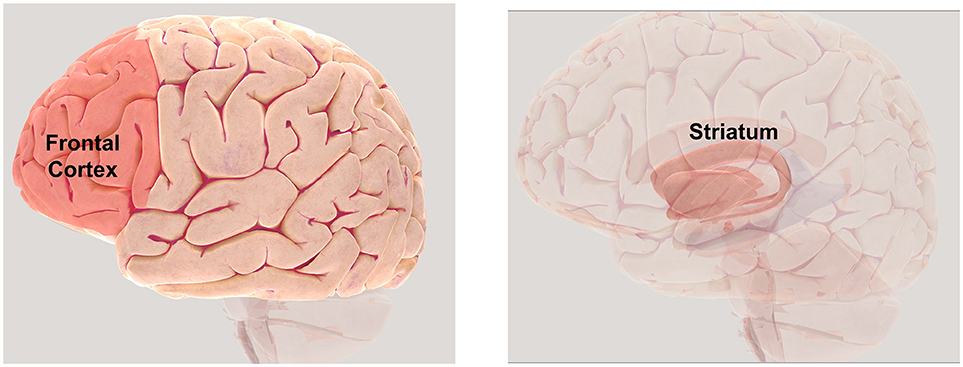
- Figure 3 - Brain areas involved in reinforcement learning.
- The frontal cortex (Left), located at the front of the brain (behind the forehead), plays an important role in decision-making and the striatum (Right) shows activity related to prediction errors. Copyright Society for Neuroscience (2017). To further explore the brain using a 3D map visit http://www.brainfacts.org/3d-brain.
Still, the changes in activity that have been shown in the striatum and the frontal cortex are only a small piece of the puzzle! It is important to remember that the brain is made up of many different parts that work together to help us think and do complicated things like learn. Scientists continue to study how the striatum, frontal cortex, and other brain areas work together to help us learn from reinforcement and to ultimately help us make the best decisions we can using the information we have learned. While we covered a classic learning model—the Rescorla–Wagner model—in this article, there are many more mathematical models that try to help us understand learning and how it happens in the brain.
So, the next time you are thinking about whether to post a picture to Instagram, remember that your brain is quickly solving a math problem—without you even knowing it!
Glossary
Computational Model: ↑ A computational model is a simple, mathematical representation of a more complicated process. The reinforcement learning model described in this article is an equation that can represent the thought processes involved in some types of learning.
Prediction Error: ↑ Prediction errors represent surprise. They represent the difference between what an animal expected to experience and what it actually experienced.
Learning Rate: ↑ An animal’s learning rate represents how quickly it updates its beliefs based on new information.
Dopamine: ↑ Dopamine is a special type of chemical in the brain, called a neurotransmitter, which is often involved in signaling reward.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
[1] ↑ Rescorla, R. 1998. Pavlovian conditioning. Am Psychol. 43:151–60.
[2] ↑ Rescorla, R., and Wagner, A. R. 1972. “A theory of Pavlovian conditioning: variations in the effectiveness of reinforcement and nonreinforcement,” in Classical Conditioning II: Current Research and Theory, eds A. H. Black and W. F. Prokasy (New York, NY: Appleton-Century-Crofts). p. 64–99.
[3] ↑ Schultz, W., Dayan, P., and Montague, P. R. 1997. A neural substrate of prediction and reward. Science 275:1593–9.
[4] ↑ Dayan, P., and Niv, Y. 2008. Reinforcement learning: the good, the bad and the ugly. Curr Opin Neurobiol. 18:185–96. doi: 10.1016/j.conb.2008.08.003
