Abstract
The actions of two people can often become coordinated, and such behavior occurs naturally. This study examined action coordination that occurred between three people in a “triadic jumping” game. The triads performed two patterns of coordination that changed based on the differing shape of the jumping space. When the space next to each jumper was equally aligned (i.e., symmetrical), all three jumpers had an equal opportunity to become the lead (first) jumper. However, when the space was not equally aligned (i.e., asymmetrical), only the member who had open space next to her or him could become the lead jumper. We gave no instructions to engage in this behavior, and the members of the triad never verbally communicated or strategized together. Thus, teamwork (symmetry-breaking pattern) among the three jumpers changed according to the symmetry of the jumper-space layout.
Take the Pizza! … Right or Left?
Imagine that you and two friends are going to eat a pepperoni pizza that is divided into three equal slices. Moreover, imagine that the cut separating two slices is directly in front of you and one of your friends asks you to take a slice; this is illustrated in Figure 1A. When you choose your slice of pizza, you will choose either the slice to your right or the slice to your left. Once you make your choice, however, your friends have less freedom to choose and are more-or-less restricted to taking the slice from the same relative side as you (Figures 1B,C).
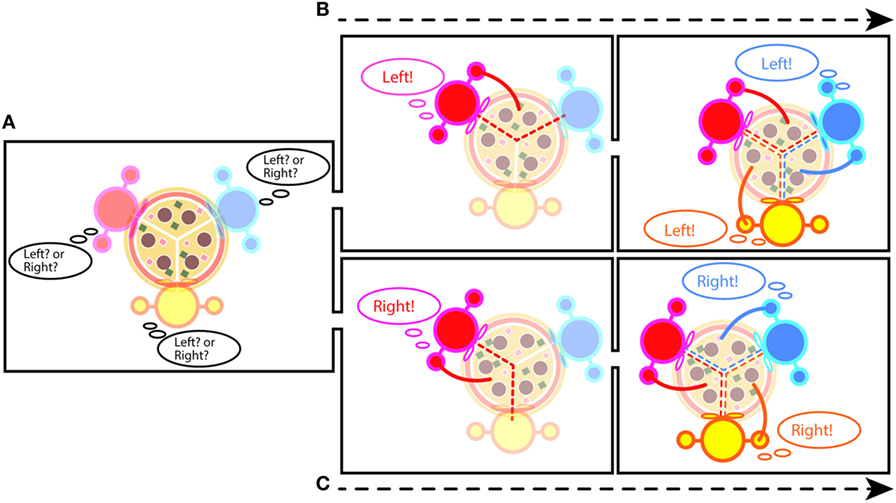
- Figure 1 - An example of symmetry breaking.
- A. Three people are sitting around a pizza. The pizza is symmetrical. B,C. If someone takes the slice from his/her left-hand side, the slice available for each other person suddenly becomes the one on his/her left-hand side. If someone takes the right-hand slice, the slice available for each other person becomes the right-hand slice.
This is an example of a “symmetry breaking.” “Symmetry,” with regard to the pizza example, means that things look the same on both sides for all the people involved. Before any single person takes a slice, all three people have the option of the slice to their left or the slice to their right (Figure 1A). When the symmetry breaks, same things on both sides turn to be different. Using our example, once the first person takes a slice on his/her right, everyone else will take the slice on their right (Figures 1B,C). As a result, each person would own “only” the right-hand slice and the slice on the left would be owned by the person to the left. In other words, once one person takes a slice, the symmetry of the situation is broken, with the choice made by the first person spreading throughout the group. Thus, symmetric state breaks into a non-symmetric state (also see Glossary).
Importantly, symmetry breaking not only plays a role in the way a group of individuals eats a pizza but it also determines the patterns of behavior individuals show when they perform all kinds of tasks. For example, when two individuals are walking directly toward each other on a sidewalk, the person who moves to the left or right first defines the direction of movement for the second person. This is something that most of us have experienced in everyday life. Of course, most of us have also experienced what happens if the symmetry is not broken: an awkward back-and-forth dance as you and the approaching walker rapidly move left and right at the same time. In this situation, as in most cases of social (and individual) behavior, symmetry breaking is very important for effective organization of behavior and performance; symmetry breaking defines how individuals move together in harmony. So, understanding how symmetry breaking influences human behavior and social interactions provides deep insights into how groups of individuals share an environmental space together (such as a crosswalk, a workspace or a playground).
Who Will be the Leader in a Three-Player Jumping Game?
Returning to the pizza example described above, the symmetry-breaking hypothesis is that the person who takes the first slice determines the pizza-slice location of the other people sharing the pizza. We tested this hypothesis using a slightly more difficult (and less messy) task than pizza eating, called a triadic jumping task. Triadic means there were three players in the game. The top-left panel in Figure 2A shows the layout of the game, which consisted of three hula hoops. Each individual in the game (one shown in red, one in blue, and one in yellow) was asked to stand in the center of a different hoop. We played a “tic-toc-ping” metronome sound, with each tone separated by 1 s. Every 3 s, when the “ping” tone sounded, all three players in the group had to jump simultaneously into the hoop to their left or right. To be successful, all three players had to jump in the same direction to avoid collision, and they had to keep playing the game until they had jumped 20 times without colliding.
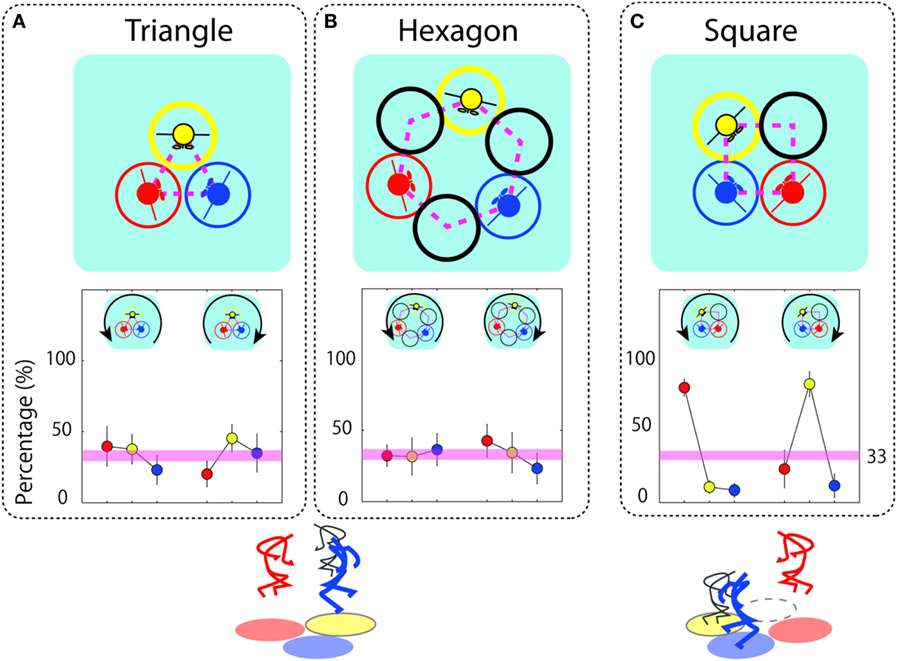
- Figure 2 - Percentage of trials in which the red, blue, or yellow player jumped first.
- A. Triangle, B. hexagon, and C. square. Upper panels: arrangement of the hoops and jumpers in the three-hoop, six-hoop, and four-hoop layouts. Lower panels: percentage of time each player jumped first when the players jumped in counterclockwise and clockwise directions. In the symmetrical layouts (triangle and hexagon), each person jumped first with an almost equal probability of 33% (= 100/3, indicated by the lower pink line). In contrast, in the asymmetrical square layout, someone who had an open space in the jumping direction almost always jumped first.
We paid close attention to which person jumped first during successful jump events (jumps when there were no collisions). We found that the chances of each person jumping first was one out of three, or approximately 33%, regardless of their hoop location, meaning that everyone had an equal chance at being the “lead jumper” in this game. We also noticed that the players changed jump directions, even though they never talked about the jump direction and no one instructed them how to coordinate their jump directions. The central question was “How do they successfully perform this task?” Please try the task yourself with some friends: although you may collide several times during your first few tries, after a short period of practice with the same people you will be able to perform the task successfully, also successfully coordinate to change jumping direction.
What Happens When We Add More Hoops to the Game?
To make the task a little more interesting, the players also performed the triadic jumping task in a layout with six hoops (Figure 2B). If you want to try this, align six hoops in the shape of hexagon, with the three players positioned so that there is an open hoop between each of them (the players will form an equilateral triangle). Try jumping with your friends. Is there any change in the timing of the triadic jump?
You will probably observe that, for both the three-hoop and six-hoop layouts, players take turns in the role of lead jumper – everyone has an equal chance of jumping first. We show this result in the lower panel of Figure 2B. Everyone has the same action possibilities (symmetry), and we saw that each player took a turn breaking the symmetry during the course of the game, that is, no one player always jumped first in either the three- or six-hoop layout.
We then asked students to jump in a four-hoop layout. The timing of the jump was quite different from that observed in the triangle (three-hoop) or hexagon (six-hoop) layouts. Upper panels of Figure 2C show the four-hoop layout. The hoops were aligned in the shape of a square, and three players were placed in three of the four hoops. A player located in a specific location jumped first in almost all successful cases. Who was the leader? This is indicated in the bottom panel of Figure 2C. The players jumped in both directions. The yellow player became the leader (jumped first) in most cases when the players jumped in a clockwise direction, and the red player became the leader when they jumped in a counterclockwise direction. Thus, the player who had open space in the jumping direction became the leader.
When the three players used a triangle- or hexagon-shaped hoop layout, the location of the players was not related to who jumped first. However, when the players shared a square play area, only someone who had open space in the jumping direction became the leader. What is the difference in the geometrical shape of the alignment of the players between the two shapes of hoops? In Figure 2B, you can also see that all players in a hexagonal hoop layout have open space on both sides of them. Recall the word “symmetry”: all players equally have or do not have open space next to them in the hexagon and triangle hoop layouts, so that the alignment of the three players in these two layouts is symmetrical. Then, let us inspect the square hoop layout in Figure 2C. We can see that the blue player does not have an open space on either side, whereas the yellow player only has open space in the clockwise direction and the red player only in the counterclockwise direction. Therefore, this hoop layout is less symmetrical compared with the triangle or hexagon hoop layouts. In the symmetrical hoop layouts, everyone has (or does not have) open space next to them. So, the shape of the symmetrical hoop layout determines the coordination between players that happens when they play the game, because anyone has the potential to jump first and become the leader. In contrast, for the asymmetrical layout, there was not an equal amount of open space between every player. Therefore, the player who had an open space next to him/her had a greater chance to become the leader.
Great Teamwork in Two- and Four-Legged Animals
In the triadic jump, all players had to jump together when a metronome tone was heard. Symmetry was broken by the player who jumped first and the “breaking pattern” changed according to the shape in which the hoops were arranged. Everyone equally had or did not have open space next to them in the hexagon and triangle hoop layouts. In these symmetrical layouts, everyone had an equal chance to be the leader, meaning that everyone’s role was also “symmetrical.” However, in asymmetrical layouts like the square, only someone who was located at a particular position, with space next to them, would become the leader; so, the leadership role was also “asymmetrical.” These patterns of symmetry breaking are defined by a kind of mathematics known as group theory. In short, we can predict the set of possible rotation patterns that leave a shape of organization the same. If you look at the three-hoop, four-hoop, and six-hoop layouts in Figure 2, it is easy to see that the three-hoop and six-hoop layouts are much more symmetrical than the four-hoop situation. If you ignore the color of the players, the three- and six-hoop layouts can be rotated by 120°, 240°, and 360° and look exactly the same. In contrast, for the four-hoop layout, the only way the layout will look exactly the same is if it is rotated 360° – in a full circle. Think about this in relation to the patterns of behavior observed in the triadic jumping task: three possible leaders in the three- and six-hoop situations compared to only two (or one for each direction) possible leaders in the four-hoop situation – there is a mapping between the symmetries of task space and the behavioral actions observed.
In addition to triadic jumping, the theory of symmetry-breaking and group theory also defines the patterns of how humans and animals walk. The walking pattern is also called the gait. For instance, suppose you are standing with both feet on the ground. You can move forward or backward from this posture. Now, once your body tilts forward, one foot will begin to lift from the ground and you will be forced to move forward. At that point, the symmetry that existed when both feet were in contact with the ground is broken by the forward tilt of the body and the organization of your walking action emerges. Jumping is another possible movement pattern that is predicted from the symmetry of a bipedal (two-legged) system, as illustrated in Figure 3A.
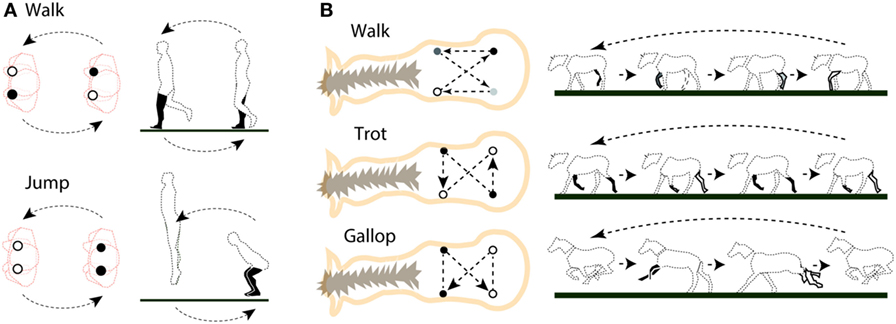
- Figure 3 - A. Symmetries of human leg positions while walking and jumping. Top: walk. Bottom: jump. Left: two circles in the human figure seen from top down (orange outline) show the locations of both feet (black: foot is on the ground, white: foot is in the air). The arrows represent the direction of the switch between leg positions. Right: change in posture can be seen when the human body is viewed from side. The color of the leg(S) corresponds to those in the left images. B. Symmetries of horse leg positions while walking and running.
- Top: slow walk. Middle: fast walk (trot). Bottom: fast run (gallop). Left: arrows represent the order in which the horses’ hooves land. Two circles connected by a dotted line (without an arrow) show the hooves landing at the same time. Right: change in posture can be seen when the horse is viewed from the side. The color of the leg(s) corresponds to those in the left images.
According to Golubitsky et al. [1], group theory predicts six patterns of gait for an animal with four legs. In Figure 3B, we show three patterns out of six, including a walking gait for a horse. When a walking horse speeds up and begins to trot (middle row in Figure 3B), either the right or left front leg and the hind leg on the opposite side are simultaneously lifted and land alternately on the ground (each pair of front and hind leg are lifted and land one at a time). As the horse increases its speed, however, it begins to grab and kick the ground with both hind legs, and after a jump, the horse lands on the ground with both front legs (“gallop”; bottom row of Figure 3).
A horse can achieve such smooth transitions between different gaits because of the structure of its nervous system, which sends signals to the muscles of the four legs. We suggest that triadic jumpers are also connected to each other. Of course, the players are not connected by a nervous system, but rather through vision, through which they communicate what they plan to do and receive information that tells them what the others plan to do. Triadic jumpers and, of course, horses, do not have any knowledge of the complicated mathematics of symmetry or group theory. But, their behavior is organized according to these mathematical rules. We think that the laws of symmetry and symmetry breaking may also apply in other situations, like the patterns of teamwork seen in football and basketball, as well as in other types of human behaviors.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Glossary
Symmetry breaking: ↑ A spontaneous (i.e., naturally occurring) phenomenon by which a system in a symmetric state ends up in a non-symmetric state.
Symmetry: ↑ An object (or action) that looks identical to its original shape after being rotated or reversed. For example, the letter M has vertical symmetry in shape, while E has horizontal.
Original Source Article
↑ Kijima, A., Shima, H., Okumura, M., Yamamoto, Y., and Richardson, M. J. 2017. Effects of agent-environment symmetry on the coordination dynamics of triadic jumping. Front. Psychol. 8:3. doi:10.3389/fpsyg.2017.00003
Reference
[1] ↑ Golubitsky, M., and Stewart, I. 2003. The Symmetry Perspective: From Equilibrium to Chaos in Phase Space and Physical Space. Vol. 200. Springer Science & Business Media.
