摘要
两个人的行为往往可以协调起来, 这种行为是自然发生的。在“三人跳”游戏中, 三个人的动作会使用两种协调模式, 这取决于游戏中跳跃空间的形状。当每个人旁边的空间相等时 (即对称), 三个人都有机会成为第一个起跳的人;然而, 当空间不相等时 (即非对称), 只有旁边开放空间较大的人才能成为第一个起跳的人。三个人之间的团队合作 (打破对称模式) 随着起跳空间布局的对称性而改变。
想象一下, 你和两个朋友要吃一份披萨, 它被分了成三等份。你的面前有两片, 你的一个朋友让你拿一片。如图 1A 所示, 你会选择你右边的那片或你左边的那片。一旦你做出了选择, 你的朋友就没有选择了, 只能拿剩下的部分 (图 1B, C)。
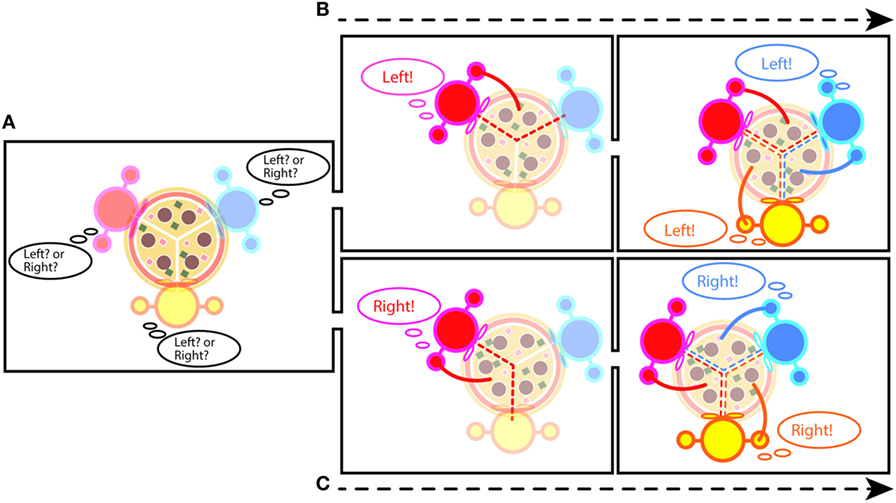
- 图 1 - 对称性破坏的例子 A. 三个人围坐在披萨旁, 披萨是对称的。B, C. 如果某个人从左手边拿了一片, 那么另一个人可以拿的那片就会变成他左手边的那片。如果某个人拿走了右手边的那片, 那么另一个人可以拿的那片就变成了右手边的那块。
这是一个“对称性破坏”的例子。以披萨为例, “对称”意味着所有人看到的东西都是一样的。在任何人拿披萨之前, 三个人都可以选择左边的那片或右边的那片 (图 1A)。当对称性被打破时, 两边相同的东西会变得不同。在这个例子中, 一旦第一个人拿了右边那片, 其他人也会拿右边那片 (图 1B, C)。结果, 每个人都只拥有右边的那片披萨, 而左边的那片属于每个人左边的人。换句话说, 一旦一个人拿了一片, 对称性就会被打破, 第一个人做出的选择就会在整个群体中传播。因此, 对称状态变为非对称状态。
重要的是对称性的破坏不仅影响了一群人吃披萨的方式, 还决定了个体在执行各种任务时的行为模式。例如, 当两个人在人行道上走向对方时, 第一个向左或向右转的人决定了第二个人的走路方向。这是我们大多数人在日常生活中都经历过的事情。当然, 大多数人也都经历过假如对称性没有被打破会发生的事情: 你和对方都在笨拙的来回移动。在这种情况下, 正如大多数社会 (和个人) 行为的情况一样, 对称性的打破对于有效的行为组织和表现非常重要;对称性的打破决定了个体如何和谐地行动。因此, 了解对称性破坏如何影响人类行为和社会互动, 可以让我们深入了解一群人如何共享一个环境空间 (比如人行横道、工作空间或游乐场)。
谁将成为 ''三人跳'' 的领跳者?
回到上面描述的披萨例子, 打破对称性的假设是: 拿第一片披萨的人决定了其他人的披萨位置。我们用一个比吃披萨稍微难一点的任务来检验这个假设, 这个任务叫做“三人跳”。游戏中有三个玩家, 图 2A 中的左上角显示了游戏的布局, 它由三个圆圈组成。游戏中的每个人 (一个红色的, 一个蓝色的, 一个黄色的) 站在一个不同的圆圈中。我们播放了“嘀-嗒-嘭”的声音,每个音之间间隔 1 秒。每隔 3 秒, 当“嘭”的声音响起时, 组里的三名玩家必须同时跳到他们左边或右边的圆圈里。为了成功, 所有的三个玩家必须朝同一个方向跳以避免碰撞, 他们需要一直玩游戏直到连跳了 20 次没有发生碰撞。
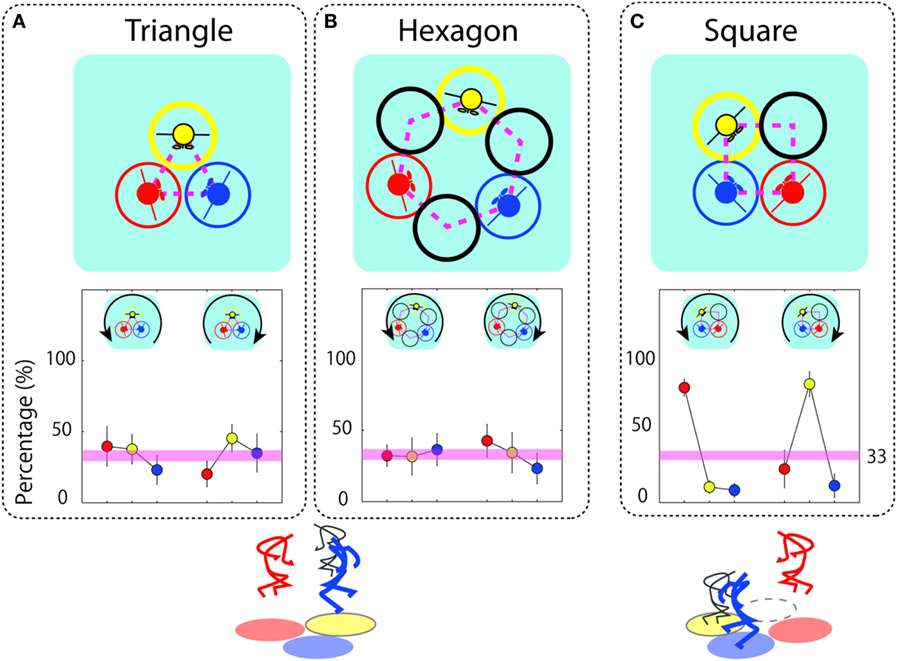
- 图 2 - 红色、蓝色或黄色玩家先跳的百分比 A. 三角形, B. 六边形, C. 正方形。上半部分: 在三圈、六圈、四圈布局中安排的圆圈和起跳者。下半部分: 当玩家以逆时针和顺时针方向跳跃时, 每个玩家先跳的百分比。在对称布局中 (三角形和六边形), 每个人先跳的概率几乎相等, 为 33% (= 100/3, 由下面的粉红色的线表示)。相反, 在不对称的正方形布局中, 在跳跃方向上有开放空间的人几乎总是第一个起跳。
我们密切关注在成功的跳跃事件 (没有碰撞的跳跃) 中是谁先跳。我们发现, 无论他们圆圈的位置在哪里, 每个人先跳的概率是三分之一 (大约 33%), 这意味着每个人都有平等的机会成为“ 领跳”。我们也注意到玩家会改变跳跃方向, 尽管他们从未讨论过跳跃方向, 也没有人指导他们如何协调跳跃方向。他们如何成功地完成这项任务?你可以和一些朋友一起这试一试: 尽管在最初的几次尝试中可能会发生碰撞, 但是在与相同的人进行短时间的练习后, 你们就能够成功地执行这个任务, 并成功地协调改变跳跃方向。
当我们在游戏中添加更多的圆圈时会发生什么?
为了让这个任务变得更有趣, 玩家还在一个有六个圆圈的布局中玩“三人跳”的游戏 (图 2B)。如果你想试试这个, 可以把 6 个圆圈排成六边形, 让 3 个玩家站好, 两两之间都留下一个圆圈 (玩家们会形成一个等边三角形)。试着和你的朋友一起跳。这是“三人跳”的时间会有什么变化吗?
你可能会注意到, 在三圈和六圈的布局中, 玩家都是轮流领跳的, 每个人都有相同的机会先跳。图 2B 的下半部分显示了这个结果。每个人都有相同的动作可能性 (对称性), 我们看到每个玩家在游戏过程中都打破了对称性, 也就是说, 没有一个玩家总是在三圈或六圈的布局中第一个起跳。
然后, 研究人员让他们跳一个四圈的布局。跳跃的时间与观察到的三角形 (三圈) 或六边形 (六圈) 布局有很大的不同。图 2C 的上半部分显示了四圈布局。圆圈排成正方形, 三名玩家进入四个圆圈中的三个。几乎在所有成功的跳跃中, 位于特定位置的玩家都是先起跳的。谁是领跳者?如图 2C 的下半部分所示, 玩家向两个方向跳跃。大多数情况下, 当玩家顺时针方向跳跃时, 黄色玩家领跳 (先跳跃);而当玩家逆时针方向跳跃时, 红色玩家会领跳。因此, 在跳跃方向上有空位的玩家成为了领跳者。
当三名玩家使用三角形或六边形的圆形布局时, 玩家的位置与谁先跳无关。然而, 当玩家共享一个方形的游戏区域时, 只有在跳跃方向上有开放空间的人才会成为领跳者。两种圆圈中玩家排列的几何形状有什么不同?在图 2B 中, 你还可以看到所有的玩家在一个六边形的环形布局中, 他们的两边都有开放空间。回忆一下“对称”这个词: 在六边形和三角形的圆圈布局中, 所有的玩家旁边都有或没有开放空间, 所以这三个玩家在这两个布局中的排列是对称的。再观察图 2C 中的方形布局, 我们可以看到蓝色的玩家两边没有开放空间, 而黄色玩家只有顺时针方向的开放空间, 红色玩家只有逆时针方向的开放空间。因此, 这种圆圈布局与三角形或六边形的圆圈布局相比, 不那么对称。在对称的圆圈布局中, 每个人旁边都有 (或没有) 开放空间。所以, 对称的圆圈布局的形状决定了玩家在玩游戏时的协调性, 因为每个人都有先跳起来成为领跳者的可能。相反, 对于非对称布局, 每个玩家之间并没有相同的开放空间。因此, 旁边有开放空间的玩家更有机会成为领跳者。
''两条腿'' 和 ''四条腿'' 的出色团队合作
在三人跳游戏中, 当听到播放的声音时, 所有玩家必须一起跳。第一个跳的人打破了对称, “打破模式”也随着圆圈的形状而改变。在六边形和三角形的圆圈布局中, 每个人旁边都有或没有开放空间。在这些对称的布局中, 每个人都有平等的机会成为领跳者, 这意味着每个人的角色也是“对称的”。然而, 在正方形这样的非对称布局中, 只有位于特定位置, 旁边有空间的人才会成为领跳者。所以, 领跳角色也是“不对称的”。我们可以预测一组可能的跳跃模式, 使组织的形状保持不变。看看图 2 中的三圈、四圈和六圈布局, 很容易发现三圈和六圈布局比四圈布局对称得多。如果忽略玩家的颜色, 三圈和六圈的布局可以旋转 120°、240° 和 360°, 而且看起来完全一样。相比之下, 对于四圈布局, 布局看起来完全相同的唯一方法是旋转 360°——旋转一整圈。思考一下在“三人跳”任务中观察到的行为模式: 三圈和六圈布局中 3 个可能的领跳者, 四圈布局中 2 个可能的领跳者 (或每个方向上 1 个可能的领跳者), 任务空间的对称性与观察到的行为反应之间存在对应关系。
除了三人跳外, 人类和动物的行走模式也有类似的特点。行走模式也叫步态。例如, 假设你双脚着地站着, 你可以从这个姿势向前或向后移动。现在, 一旦你的身体向前倾斜, 一只脚将开始从地面抬起, 你就会被迫向前移动。当双脚与地面接触时存在的对称性被身体的前倾打破, 你的步行动作就开始了。跳跃是另一种可能的运动模式, 如图 3A 所示。
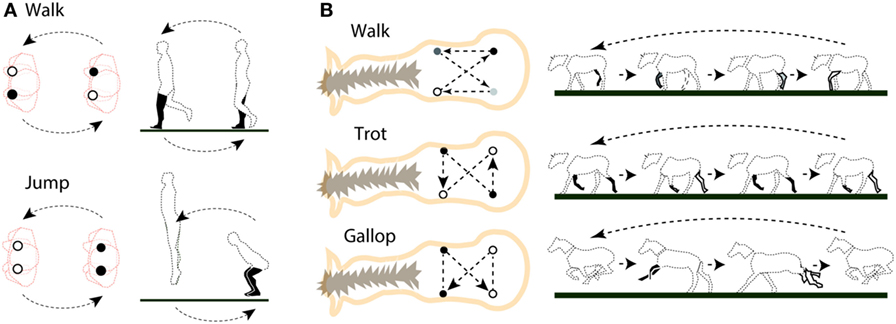
- 图 3 - 腿部位置的对称性 A. 人类行走和跳跃时腿部位置的对称性。上图: 行走。下图: 跳。左图: 从上往下看人体轮廓上的两个圆圈 (橙色轮廓) 显示了两只脚的位置 (黑色: 脚在地上, 白色:脚在空中)。箭头表示腿部位置之间转换的方向。右图: 从侧面看人体姿势的变化。腿的颜色与左图的颜色一致。B. 步行和跑步时马腿位置的对称性。上图: 缓慢行走。中间: 快步走 (小跑)。下图: 快跑 (飞奔)。左图: 箭头表示马蹄着地的顺序。由虚线 (没有箭头) 连接的两个圆圈表示马蹄同时着地。右图: 从侧面看马的时候可以看到姿势的变化。腿的颜色与左图的颜色一致。
Golubitsky 等人 [1] 预测了四足动物的六种步态模式。在图 3B 中, 我们展示了六种模式中的三种, 包括马的步态: 马加速行走并开始小跑 (图 3B 中间行), 右前腿或左前腿和后腿的另一侧交替同时提起或落地 (每一对前、后腿提起、落地一次);然而, 当马的速度加快时, 它开始用两条后腿抓地和踢地、跳跃后, 用两条前腿着地 (“飞奔”;图 3 最下面一行)。
马之所以能在不同的步态之间实现如此流畅的转换, 是因为神经系统向四条腿的肌肉发送信号。我们认为“三人跳”中的三人也是彼此相连的。当然, 这些玩家并不是由神经系统连接起来的, 而是通过视觉——他们通过视觉传达他们的计划, 并接收信息。对称性和对称性破坏的规律也适用于其他情况, 比如足球和篮球中的团队合作模式, 以及其他类型的人类行为。
致谢
脑与心智毕生发展研究中心发展人口神经科学研究中心中文翻译 & 编辑: 刘斯漫范雪如中文审校: 左西年感谢脑与心智毕生发展研究中心、发展人口神经科学研究中心对本文中文翻译的贡献。感谢刘斯漫、范雪如对本文中文翻译及编辑的贡献;感谢左西年对本文中文审校的贡献。
术语表
对称性破坏 (Symmetry breaking): ↑ 一个处于对称状态的系统变为非对称状态的自发现象。
对称性 (Symmetry): ↑ 一个物体 (或动作) 在旋转或翻转后看起来与原来的形状相同。例如, 字母 M 在形状上垂直对称, 而 E 水平对称。
利益冲突声明
作者声明, 该研究是在没有任何可能被解释为潜在利益冲突的商业或财务关系的情况下进行的。
原文
↑ Kijima, A., Shima, H., Okumura, M., Yamamoto, Y., and Richardson, M. J. 2017. Effects of agent-environment symmetry on the coordination dynamics of triadic jumping. Front. Psychol. 8:3. doi: 10.3389/fpsyg.2017.00003
参考文献
[1] ↑ Golubitsky, M., and Stewart, I. 2003. The Symmetry Perspective: From Equilibrium to Chaos in Phase Space and Physical Space. Vol. 200. Springer Science & Business Media.
