תַקצִיר
בחיי היומיום קורה לעתים קרובות ששני אנשים פועלים בתיאום באופן טבעי ובלי שסיכמו זאת מראש. מחקר זה עסק בתיאום פעולות בין שלושה משתתפים במשחק קפיצה. בניסוי התברר שהשלישיות פעלו לפי אחד משני דפוסי תיאום, תלוי בצורה של מרחב הקפיצה: כאשר האזור הסמוך לכל שחקן היה ערוך באופן זהה (כלומר, כל המערך היה סימטרי), הייתה לכל שחקן הזדמנות שווה להיות הקופץ המוביל (הראשון). אבל כשהמרחב לא היה סימטרי, רק שחקן שהיה לידו מקום פנוי הוביל את הקפיצה. המשתתפים לא קיבלו הוראות להתנהג באופן כזה, ולא היו ביניהם תקשורת מילולית או תכנון מראש. המסקנה היא שעבודת הצוות ביניהם (דפוס שבירת הסימטריה) השתנתה לפי הסימטריה של מרחב הקפיצה.
קחו לכם פיצה!... משמאל או מימין?
תארו לכם שאתם ועוד שני חברים יושבים לאכול פיצה טעימה שמחולקת לשלושה חלקים שווים. תארו לכם גם שהחתך בין שני חלקים נמצא בדיוק מולכם, ושאתם מתבקשים לקחת את המשולש הראשון (איור 1A). אתם יכולים כמובן לבחור במשולש שמימינכם או במשולש שמשמאלכם. אבל מרֶגע שתבחרו, לחברים שלכם לא יהיה חופש בחירה כזה: בעצם הם יכולים רק לבחור במשולש הנמצא, יחסית אליהם, באותו צד שבחרתם אתם (איורים 1B ו-1C).
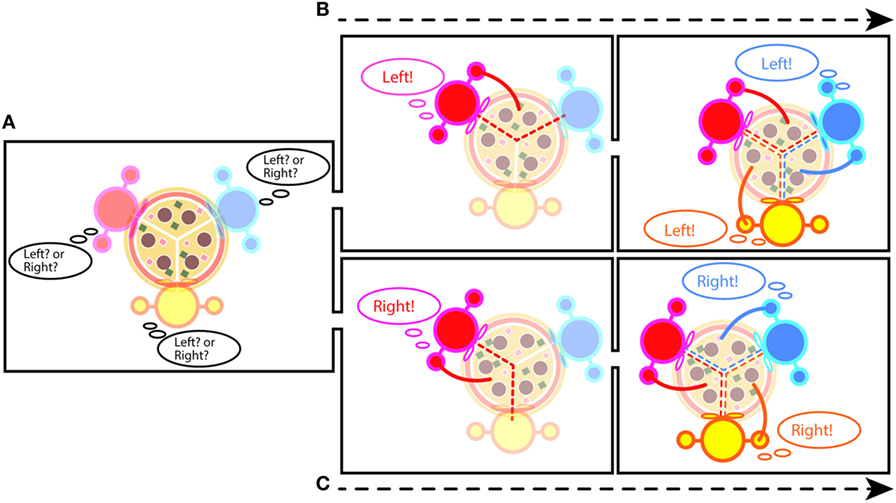
- איור 1 - דוגמה לשבירת סימטריה:
- A. שלושה אנשים יושבים סביב פיצה. הפיצה היא סימטרית. כל סועד יכול לקחת את השליש שמימינו או שמשמאלו. B. אם אדם אחד לוקח את המשולש שמשמאלו, כל הסועדים האחרים הופכים פתאום ל“בעלים” של המשולשים שמשמאלם בלבד. C. ולהיפך – אם אדם אחד לוקח את המשולש שמימינו, כל הסועדים האחרים הופכים פתאום ל“בעלים” של המשולשים שמימינם.
זוהי דוגמה לשבירת סימטריה. סימטריה, בהקשר זה, פירושה ששני צדי התמונה נראים זהים לכל המעורבים בדבר. כל עוד אף אחד מהנוכחים לא לקח משולש פיצה, יש לכל אחד מהם אפשרות לבחור במשולש שמשמאלם או במשולש שמימינם (איור 1A). ברגע שהסימטריה נשברת, המצב כבר לא זהה בשני הצדדים. בדוגמה שלנו, אחרי שהמשתתף הראשון לוקח את משולש הפיצה שמימינו, כל המשתתפים האחרים ייקחו גם הם את המשולשים שמימינם (איורים 1B, 1C). כלומר, כל משתתף יהיה ה“בעלים” של המשולש שמימינו בלבד, והמשולש שמשמאלו יהיה “שייך” למשתתף שמשמאלו. ברגע שאדם אחד בוחר משולש פיצה, הסימטריה שבמצב נשברת, והבחירה שלו מתפשטת גם בשאר הקבוצה. כך נשבר המצב הסימטרי והופך למצב לא סימטרי (ראו גם מילון מונחים).
שבירת סימטריה היא חשובה כי היא ממלאת תפקיד לא רק באופן שבו קבוצות של יחידים אוכלות פיצה, אלא גם קובעת את דפוסי ההתנהגות של יחידים כשהם עושים מגוון פעולות. למשל, כאשר שני אנשים הולכים זה מול זה ברחוב, מי שזז ראשון שמאלה או ימינה כדי לפנות את הדרך קובע לאיזה כיוון יזוז זה שבא מולו. רובנו נתקלנו במצבים כאלה בחיי היומיום. רובנו גם ראינו, כמובן, מה קורה כשהסימטריה לא נשברת: ריקוד קטן ומסורבל שבו אתם והאדם שמולכם זזים זה מול זה מצד לצד. במצב זה, ובתחום ההתנהגות החברתית (והאישית) בכלל, שבירת סימטריה היא חיונית לארגון יעיל של התנהגות ופעולה. היא קובעת איך יחידים ינועו יחד בתיאום. לכן, אם נִלמד איך שבירת סימטריה משפיעה על ההתנהגות והיחסים החברתיים של בני אדם, נוכל להבין לעומק איך קבוצות של יחידים מצליחות לחלוק מרחב משותף (כמו למשל מעבר חציה, משרד, או מגרש משחקים).
מי יהיה המוביל במשחק קפיצה של שלושה שחקנים?
אם נחזור לדוגמה עם הפיצה, ההשערה שלנו לגבי שבירת הסימטריה הייתה שמי שלוקח את המשולש הראשון קובע את מיקומֵי המשולשים ה“שייכים” לאחרים. בדקנו את ההשערה הזאת באמצעות משימה קצת יותר קשה (ופחות מלכלכת) מאכילת פיצה: משימת קפיצה בשלישייה. בשרטוט השמאלי העליון באיור 2 תראו במבט מלמעלה את שטח המשחק הראשון: שלושה חישוקים מונחים בצורת משולש. כל שחקן (השחקנים מסומנים בנקודה אדומה, נקודה צהובה ונקודה כחולה) התבקש לעמוד במרכז חישוק אחר. השמענו מקצב חוזר של שלושה צלילים עם מרווח של שנייה ביניהם: “טיק-טוק-פּינג”. מדי שלוש שניות, כל פעם שנשמע הצליל “פּינג”, נדרשו שלושת המשתתפים לקפוץ בבת אחת ימינה או שמאלה לחישוק אחר. כדי להצליח, היה על שלושתם לקפוץ לאותו כיוון על מנת לא להתנגש. הם התבקשו להמשיך לשחק עד שישיגו 20 הצלחות כאלה.
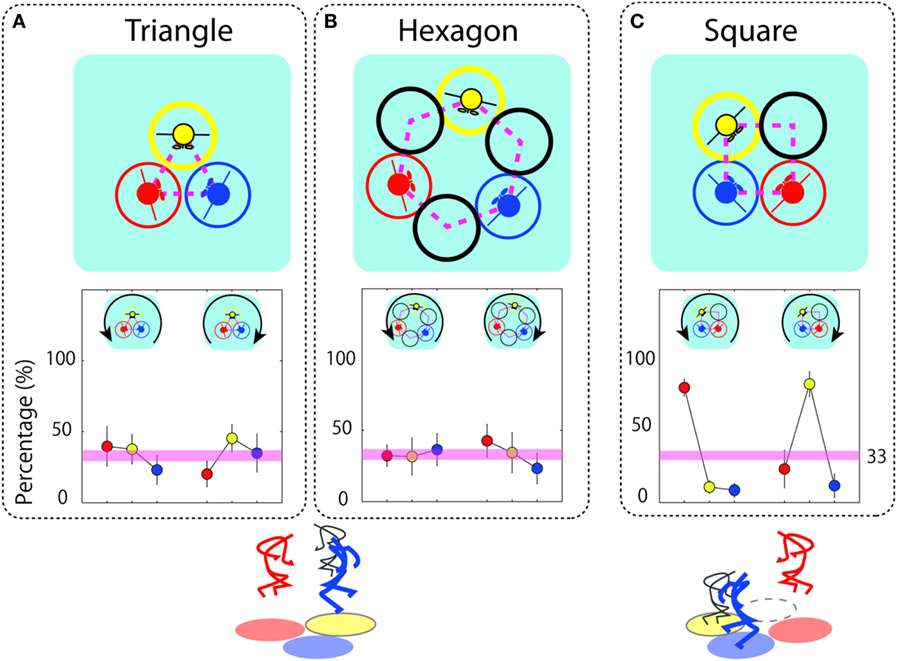
- איור 2 - מספר הפעמים שבהן כל שחקן הוביל את הקפיצה.
- A. במערך המשולש, B. במערך המשושה, C. במערך המרובע. בחלק העליון של כל תרשים, רואים את מיקום החישוקים והשחקנים, ובחלק התחתון – גרף המראה בכמה מהקפיצות הוביל כל שחקן. כל גרף מחולק לשניים – נגד כיוון השעון (צד שמאל) ועם כיוון השעון (צד ימין). במערכים הסימטריים (המשולש והמשושה), מספר הפעמים שבהן כל שחקן קפץ ראשון היה כמעט שווה – סבירות של 33% (100/3. מסומן בקו ורוד). לעומת זאת, במערך האַסימטרי (המרובע), מי שקפץ ראשון היה כמעט תמיד רק מי שהיה לידו מקום פנוי בכיוון הקפיצה.
בדקנו מי מהשלושה קפץ ראשון בקפיצות מוצלחות (ללא התנגשויות). גילינו שכל שחקן קפץ ראשון בשליש מהקפיצות המוצלחות, כלומר 33% בערך, בלי קשר לחישוק שבתוכו עמד – כלומר, לכולם היו סיכויים שווים להיות “הקופץ המוביל” במשחק. שמנו לב גם לכך שהמשתתפים החליפו את כיוון הקפיצה מפעם לפעם, אף על פי שלא דיברו על כך מראש ולא קיבלו הוראות לגבי תיאום של כיוונים. השאלה המרכזית הייתה: “איך הם מצליחים במשימה הזאת?” אתם מוזמנים לנסות זאת בעצמכם עם חברים: בניסיונות הראשונים אולי יהיו לכם כמה התנגשויות, אבל אחרי מעט תרגול באותה שלישייה תצליחו לקפוץ, וגם לשנות מדי פעם כיוון, ללא התנגשויות.
מה קורה כשמוסיפים חישוקים?
בשלב הבא, הוספנו עוד שלושה חישוקים, כך ששלושת השחקנים השתמשו כעת ב“לוח משחק” עם שישה חישוקים (איור 2B). אם אתם רוצים לנסות זאת בעצמכם, סדרו שישה חישוקים בצורת משושה ועימדו כך שבין כל שני שחקנים יהיה חישוק פנוי (והשחקנים עומדים כך שאפשר לשרטט ביניהם משולש שווה-צלעות). נסו שוב את משימת הקפיצה. האם היה שינוי?
ודאי גיליתם שגם בגירסת שלושת החישוקים וגם בגירסת ששת החישוקים, כל שחקן מוביל בתורו, כלומר לכל אחד יש סיכוי שווה לקפוץ ראשון. הגרף בתחתית איור 2B מבטא זאת. בתחילת כל סיבוב יש לכל שחקן אפשרויות פעולה זהות, כלומר יש סימטריה, וראינו שבמהלך המשחק השחקנים שוברים את הסימטריה לפי התור, פחות או יותר – אף שחקן לא היה תמיד הקופץ הראשון במערכי שלושת החישוקים או ששת החישוקים.
בשלב הבא בניסוי השתמשנו במערך של ארבעה חישוקים, ודפוס הקפיצות השתנה לגמרי. בחלק העליון של איור 2C תראו את מערך ארבעת החישוקים. הם הונחו בצורת ריבוע, והמשתתפים עמדו בשלושה מהם. כמעט בכל הקפיצות המוצלחות הוביל שחקן שעמד במיקום מסוים. מי? הביטו בחלק התחתון של איור 2C. השחקנים קפצו לפעמים בכיוון השעון ולפעמים נגדו. ברוב הסיבובים שבהם קפצו בכיוון השעון השחקן הצהוב היה המוביל (זה שקפץ ראשון), וברוב הסיבובים נגד כיוון השעון – השחקן האדום. כלומר, השחקן שהיה לידו חישוק פנוי בכיוון הקפיצה הפך למוביל.
התברר לנו שכאשר שלושה שחקנים שיחקו במערך משולש או משושה, לא היה קשר בין המיקום שלהם לשאלה מי יקפוץ ראשון. אבל כששטח המשחק היה מרובע, הוביל רק מי שהיה לידו מקום פנוי בכיוון הקפיצה. מה ההבדל בין הצורות הגיאומטריות שיוצרים השחקנים במערכי המשחק השונים? באיור 2B תראו שבמערך המשושה יש ליד כל שחקן מקומות פנויים משני הצדדים. חישבו שוב על המונח “סימטריה”: במערך המשולש אין מקום פנוי ליד אף שחקן, ובמערך המשושה יש שני מקומות פנויים ליד כל שחקן. לכן בשני המערכים ההעמדה של השחקנים היא סימטרית. עכשיו נסתכל על המערך המרובע באיור 2C: לשחקן הכחול אין כלל מקום פנוי לידו, לשחקן הצהוב יש מקום פנוי רק בכיוון השעון, ולשחקן האדום – רק בכיוון ההפוך מכיוון השעון. לכן המערך המרובע פחות סימטרי מהאחרים, שבהם לכל השחקנים יש מקום פנוי או שלכולם אין. אם כן, הצורה של מערך החישוקים הסימטרי מכתיבה את התיאום בין המשתתפים במשחק, כי לכל אחד מהם יש פוטנציאל לקפוץ ראשון ולהיות המוביל. לעומת זאת, במערך האַסימטרי אין מקום פנוי שווה בין שחקן לשחקן. לכן, המשתתף שלידו יש מקום פנוי הוא בעל פוטנציאל גדול יותר להפוך למוביל.
“עבודת צוות” מצוינת אצל חיות הולכות על שתיים ועל ארבע
במשחק קפיצה של שלישייה, כל השחקנים נדרשו לקפוץ יחד כשהושמע צליל מסוים. השחקן שקפץ ראשון שבר את הסימטריה, ו“דפוס השבירה” השתנה לפי הצורה שבה החישוקים היו מונחים. כשהיו מונחים במשולש או במשושה, לכל שחקן היה (או לא היה) מקום פנוי לידו, בדיוק כמו לכל שחקן אחר. במערכים הסימטריים האלה היה לכל שחקן סיכוי שווה להיות המוביל – כלומר, הייתה סימטריה גם בין התפקידים. לעומת זאת, במערכים אַסימטריים כמו זה שבו יש ארבעה חישוקים ושלושה שחקנים, הוביל רק מי שנמצא במיקום מסוים (שלידו היה מקום פנוי), כך שגם תפקיד המוביל התאפיין באַסימטריה. יש ענף מתמטי הנקרא “תורת החֲבוּרות”, והוא עוסק בין השאר בדפוסים של שבירת סימטריה. באמצעות תורת החבורות אפשר לצפות את מערכת דפוסי הסיבוב האפשריים שלא ישנו את צורת הארגון. אם מסתכלים במערכים השונים באיור 2, קל לראות שהמערך המשולש והמערך המשושה הרבה יותר סימטריים מהמרובע. אם מתעלמים מהצבעים השונים המסמלים את השחקנים, אפשר למעשה לסובב את המערכים של שלושת החישוקים ושל ששת החישוקים ב-120, 240 או 360 מעלות, בלי שישתנוּ כלל. לעומת זאת, מערך ארבעת החישוקים ושלושת השחקנים יישאר כפי שהיה רק אם נסובב אותו ב-360 מעלות, כלומר סיבוב שלם שיחזיר אותו למקומו הקודם. שימו לב כיצד זה מתקשר להתנהגות של השחקנים: במשחקים שבהם יש שלושה או שישה חישוקים יש שלושה מובילים, אבל במשחק עם ארבעת החישוקים מובילים רק שני שחקנים (אחד לכל כיוון). יש הקבלה בין הסימטריה של מרחב המשימה לבין התנהגות המשתתפים.
תורת החבוּרות ושבירת הסימטריה מגדירה לא רק איך יתנהגו השחקנים במשימת קפיצה בשלישייה, אלא גם, למשל, את דפוסי ההליכה של אנשים ושל חיות. נניח לדוגמה שאתם עומדים עם שתי הרגליים על הקרקע. מתנוחה זו אפשר לנוע קדימה או אחורה. ברגע שגופכם מתחיל לנטות קדימה, רגל אחת תתרומם מהקרקע, ותהיו חייבים להתקדם. ההטיה של גופכם קדימה שוברת את הסימטריה שהתקיימה כששתי רגליכם היו על הקרקע, ומתגלה איך מאורגנת פעולת ההליכה שלכם. קפיצה היא עוד דפוס שאפשר לצפות אותו מראש אם מבינים את הסימטריה של מערכת דו-רגלית (איור 3A).
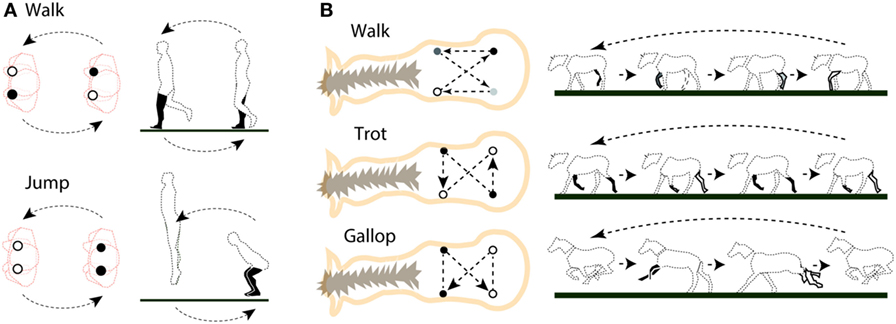
- איור 3 - סימטריות של מצב הרגליים בהליכה ובקפיצה.
- A. מצבי הרגליים אצל בני אדם בהליכה (למעלה) ובקפיצה (למטה). משמאל נראה הגוף במבט מלמעלה (בכתום). עיגול שחור מסמל רגל על הקרקע, ועיגול לבן – רגל באוויר. החיצים מראים את כיוון ההחלפה בין מצבי הרגליים. מימין נראה שינוי התנוחה במבט מהצד. גם כאן הרגל על הקרקע מסומנת בשחור, וזו שבאוויר – בלבן. B. מצב הרגליים אצל סוס בהליכה איטית (למעלה), בהליכה מהירה/ריצה קלה (באמצע) ובדהירה (למטה). משמאל נראה הסוס במבט מלמעלה, והחיצים מראים את סדר הנחיתה של הפרסות על הקרקע. שני עיגולים המחוברים בקו מקווקו בלי חץ מייצגים פרסות הנוחתות על הקרקע באותו זמן. מימין נראה השינוי בתנוחת הסוס במבט מהצד. הרגליים שעל הקרקע מסומנות בשחור, ואלו שבאוויר – בלבן.
גולוביצקי ועמיתיו [1] מסבירים שלפי תורת החבוּרות, אפשר לִצפּות שישה דפוסי תנועה אצל חיה עם ארבע רגליים. באיור 3B מופיעים שלושה מתוך ששת הדפוסים, ביניהם הליכה של סוס. כאשר הסוס מגביר את קצב ההליכה ועובר לריצה קלה (שורה אמצעית באיור 3B), הוא מרים ומוריד בכל פעם רגל קדמית אחת יחד עם הרגל האחורית הנגדית. כאשר הוא מאיץ עוד יותר ועובר לדהרה, שתי הרגליים האחוריות נוחתות בבת אחת על הקרקע ואז בועטות בה – ואחרי קפיצה, הוא נוחת על הקרקע בשתי הרגליים הקדמיות (שורה תחתונה של איור 3).
הסוס מצליח לבצע מעברים חלקים בין דרכי תנועה שונות הודות למבנה מערכת העצבים שלו, ששולחת אותות לשרירי ארבע הרגליים. ההשערה שלנו היא שגם המשתתפים במשימת קפיצה מקושרים זה לזה – לא באמצעות מערכת עצבים משותפת, כמובן, אלא באמצעות ראייה: כך הם מאותתים זה לזה מה הם מתכננים לעשות, ומקבלים מידע על התכניות של האחרים. השחקנים – וגם הסוסים, כמובן – לא מכירים כלל את המתמטיקה המסובכת של תורת החבוּרות, או הסימטריה. אבל ההתנהגות שלהם מאורגנת לפי הכללים המתמטיים האלה. אנחנו משערים שחוקי הסימטריה ושבירת הסימטריה נכונים גם למצבים אחרים, כמו דפוסי עבודת-הצוות שאפשר לראות במשחקי כדורגל וכדורסל, ובסוגים רבים אחרים של התנהגות אנושית.
מילון מונחים
שבירַת סימֶטריה (Symmetry breaking): ↑ תופעה ספונטנית (מתרחשת מעצמה, טבעית) של מעבר מערכת במצב סימטרי למצב לא סימטרי
סימֶטריה (Symmetry): ↑ עצם (או פעולה) הנראה זהה כאשר הופכים או מסובבים אותו. למשל, לאות M יש סימטריה אנכית, ולאות E סימטריה אופקית.
הצהרת ניגוד אינטרסים
המחברים מצהירים כי המחקר נערך בהעדר כל קשר מסחרי או פיננסי שיכול להתפרש כניגוד אינטרסים פוטנציאלי.
מאמר המקור
↑ Kijima, A., Shima, H., Okumura, M., Yamamoto, Y., and Richardson, M. J. 2017. Effects of agent-environment symmetry on the coordination dynamics of triadic jumping. Front. Psychol. 8:3. doi: 10.3389/fpsyg.2017.00003
מקורות
[1] ↑ Golubitsky, M., and Stewart, I. 2003. The Symmetry Perspective: From Equilibrium to Chaos in Phase Space and Physical Space. Vol. 200. Springer Science & Business Media.
