Abstract
Legend has it that the first person in ancient Greece who discovered that there are numbers that cannot be written as fractions was thrown overboard from a ship. Centuries later, while we regularly use numbers that cannot be written as fractions, those numbers that can be written as fractions remain powerful tools. What makes fractions so special? We explore how we can recognize the decimal representation of fractions and how fractions can be used to approximate any real number as closely as we wish.
On Monday morning, your friend Jordan walks up to you and says, “I’m thinking of a number between 1 and 100.” Being a good sport, you play along and guess 43. “Nope, too low!” Jordan declares. “Fine, how about 82?” you ask. “Too high!” Jordan answers. You keep guessing. 60 is too low. 76 is too high. 70 is too low. Feeling pleased that you are getting closer, you ask, “How about 75?” “You got it!” Jordan replies, and you march triumphantly off to your first class of the day.
But after class, you again run into Jordan, who has apparently been thinking about ways to stump you: why stick to positive numbers? What if you also allow negative numbers? “Now I am thinking of a number between negative 100 and 100,” Jordan says gleefully. You decide to take the bait, and you quickly discover that this does not change the game much. You guess, and by going higher and lower you get closer and closer to the target. If Jordan’s number is −32, and you have already figured out that −33 is too low and −31 is too high, then you know the answer is −32. But then you realize: there is nothing special about −100 and 100! If you start with a number between −1000 and 1000, you know you will eventually guess the correct number even if it takes a few more guesses. You march off to your second class victoriously, confident that you will be prepared for Jordan’s next challenge.
However, during that class, you realize that you have been assuming Jordan will always pick an integer. What if fractions are allowed? Suppose Jordan picks a number between 0 and 1, for example . You have to guess a number somewhere along the number line from 0 to 1. You try starting exactly in the middle and guess . Jordan tells you your guess is high, so you know the answer is somewhere on the number line between 0 and . You guess in the middle again: . Jordan says is still high, so you know the answer must be on the number line between 0 and . Continuing with your strategy, you guess . One representation of this game is shown in Figure 1. This seems like it is taking a long time! Will you ever guess the right number? Perhaps it would help if you change your strategy. Or are you doomed to be guessing forever?
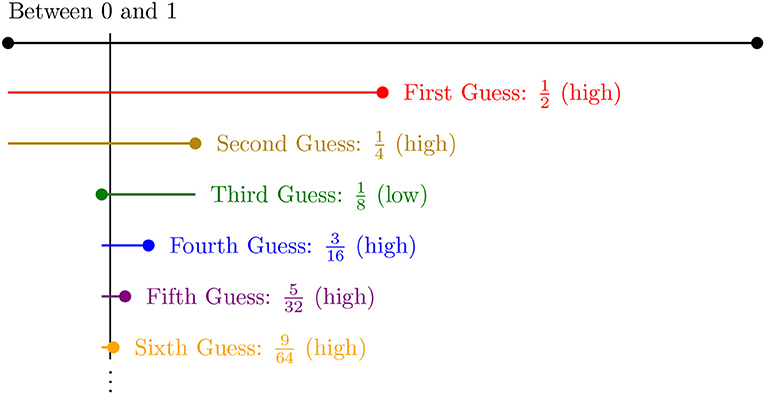
- Figure 1 - A number guessing game.
- Your friend Jordan asks you to guess a number between 0 and 1. With each guess, you halve the range where Jordan’s number might be. The dot at the end of each line segment is your guess. The position of the number you are trying to guess, , is marked by the vertical black line segment.
A New Strategy: Decimal Expansions
Let us look at these numbers in a different way and think about them as decimals instead. We can turn a fraction into a decimal by dividing the numerator by the denominator. Here is how it works for the fraction :
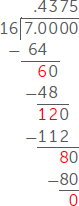
For the first step of the division, we ask how many 16’s are in 70. (Really, we are asking how many 1.6’s are in 7.0, but this is equivalent to asking how many 16’s are in 70). Since 16 × 4 = 64, we write a 4 above the 0 in 7.0. Then we subtract 64 from 70 and get 6 left over. In this case, 6 is called the remainder.
For the next step, we bring down the next 0 from 7.00. Then we ask how many 16’s are in 60. Since 16 × 3 = 48, we write a 3 above the second 0. Next, we subtract 48 from 60 to get a remainder of 12.
We continue this process, bringing down zeros after each remainder and asking how many 16’s are in the resulting number. After we have done this four times, we get a remainder of 0, which has zero 16’s in it. At this point, we are done with our long division and we can say that . If you are playing the guess-the-number game, you can arrive at this decimal version of in several short steps. The table below shows a possible way this could happen. In the table, H means your guess was too high and L means your guess was too low.

Because the decimal for the number ends, you can get the exact number by guessing one digit at a time in the decimal. Does this happen for all fractions? Let us look at the decimal for .
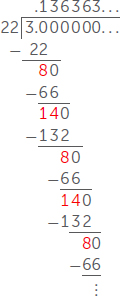
Following the same division process, we get a 1 on top with a remainder of 8, a 3 on top with a remainder of 14, a 6 on top with a remainder of 8, a 3 on top with a remainder of 14 … but wait! We have already seen these remainders, and we know that the next number on top is a 6 with a remainder of 14 again. As we continue to divide, the two repeating remainders of 8 and 14 give us repeating 3′s and 6′s in the decimal expansion for . This means that if you try to guess the number one decimal place at a time, you will be guessing forever!
Rational Numbers
All of the numbers we have considered so far are called rational numbers. A rational number is any number that we can write as a fraction of two integers (whole numbers or their negatives), a and b. This means that is a rational number since 2 and 5 are integers. Also, 3 is a rational number since it can be written as and 4.5 is a rational number since it can be written as . Even if we do not write 3 and 4.5 as fractions, they are rational numbers because we can write a fraction that is equal to each.
We have seen that some rational numbers, such as , have decimal expansions that end. We call these numbers terminating decimals. Other rational numbers, such as , have decimal expansions that keep going forever. But we do know that even the decimal expansions that do not terminate repeat, so we call them repeating decimals.
For any rational number , the only remainders we can get when we compute the decimal are the numbers 0, 1, 2, 3, …, b − 2, b − 1. For example, when we were changing into a decimal, the only options we had for remainders were 0, 1, 2, 3, …, 20, 21. Because there are only a finite number of remainders, the remainders must start to repeat eventually. This is true for all fractions whose decimals do not terminate. Even though there is a repeating pattern to the decimals for these fractions, we will never guess the exact number in the guessing game if we are guessing one decimal place at a time because the decimal goes on forever. We cannot say infinitely many digits!
We can go in the reverse direction and change decimals to fractions, too! When we have a terminating decimal expansion, such as 4.132, we can change this to a fraction using place value. The 2 of 4.132 is in the thousandths place, so . If we are starting with a repeating decimal, we have to do a bit more work to find its corresponding fraction. For example, consider 0.353535…. Call this number A. The repeating portion 35 has two digits, so we multiply A by 100 to move the decimal over two places. This gives 100A = 35.353535…. Notice that all the decimal places in A and 100A match up. We subtract A from 100A to get 99A. When we subtract the decimals, the 0.353535… is the same for both and is eliminated in the difference. Therefore, we are left with only whole numbers!
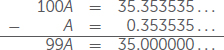
We have 99A = 35, so when we divide by 99, we get . For any repeating decimal, we can use the same process to find the corresponding fraction. We multiply by 10, 100, 1000, or whatever is necessary to move the decimal point over far enough so that the decimal digits line up. Then we subtract and use the result to find the corresponding fraction. This means that every repeating decimal is a rational number!
Irrational Numbers
What if we have a decimal expansion that does not end, but the digits do not repeat? For example, look at 0.101001000100001…. In this number, we increase the number of 0s between each pair of 1s, first having one 0 between, then two 0s, then three 0s, etc. This cannot be a rational number since we know the decimals for rational numbers either terminate or repeat. This is an example of an irrational number. An irrational number is any number that we can put on a number line that cannot be written as a fraction of whole numbers. You have probably heard about the famous irrational number π = 3.14159…, which gives the ratio of a circle’s circumference to its diameter. While this is a ratio, at least one of the circumference or diameter is not an integer, so π is not a rational number. Another irrational number is , which is the length of the diagonal of a square whose sides are length 1.
Going back to our game, all irrational and rational numbers together fill up our number line between 0 and 1. Suppose your friend Jordan could pick any number between 0 and 1 and chose an irrational number for you to guess. You would likely have a very hard time guessing the number exactly! Just like with the repeating decimal expansion of , you cannot say infinitely many digits, so this game seems very unfair.
Let us change the game so you can win! Jordan chooses three things: a number for you to guess, a range of numbers in which that number lies, and how close your guess has to be. With these new rules, Jordan chooses the number π and tells you “I’m thinking of a number between 2 and 10. See if you can guess within 0.01 of my number.” In this situation, the game could go like this:

In this new version of the game, even if Jordan changes how close you have to guess, you can always eventually get within that distance of π. You just need to get the whole number part and a certain number of decimal places correct. For example, to be within 0.1 of π, you only need to get the first decimal place correct. To be within 0.01 of π, you need to get the first two decimal places correct. To be within 0.001 of π, you need to get the first three decimal places correct. No matter how close your guess must be, you can win this new game by guessing one decimal place at a time until you have enough decimal places.
As we saw earlier, every decimal that terminates is a rational number. If we use this process of getting closer and closer to an irrational number by guessing more and more decimal places of the number, we can get a rational number that is as close as we like to our goal irrational number. In our game, this means that no matter what irrational number Jordan chooses nor how close you have to guess, you can always find a rational number that will meet the requirements. In this game, you can always win!
Conclusion
The reason this happens is that the rational numbers are dense in the real numbers. This means that between any two different real numbers, we can always find a rational number. Because real numbers have this property, we can approximate any irrational number with a rational number. Approximating an irrational number with a rational number is what you are doing in the new game when Jordan picks an irrational number.
But why would you ever need to approximate an irrational number with a rational number? Suppose you are building a wooden frame for a triangular garden bed in the shape of half the square in Figure 2. You need to cut a piece of wood that is feet long. How will you measure that length? Because is an irrational number, you cannot use your tape measure to measure it exactly! Instead, you will pick a rational number that approximates . You can choose the number of decimal digits to include in your expansion in order to get the piece of wood as close in length as you want to , the same way you chose your rational number to be as close as Jordan wanted you to get in the game.
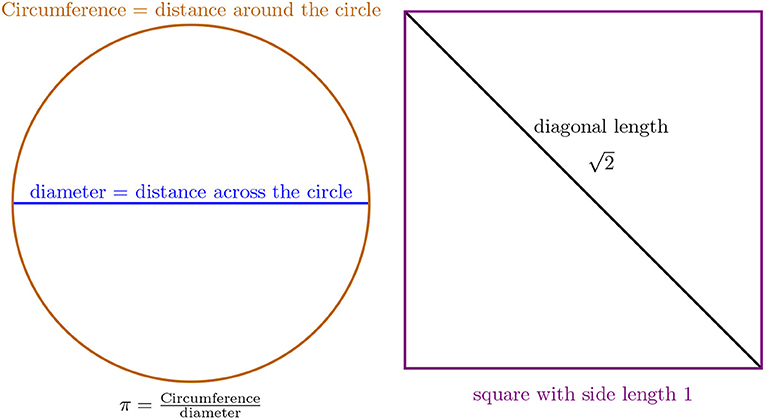
- Figure 2 - Two irrational numbers we see in geometry.
Approximating with rational numbers is a very powerful tool for doing computations, for measuring materials in construction, and for many other applications. The fact that rational numbers are dense in the real numbers is what lets us use this tool!
Glossary
Rational Number: ↑ A real number that can be written as a fraction of two integers . Decimal expansions for rational numbers can be either terminating or repeating decimals.
Terminating Decimal: ↑ A decimal expansion that only has a finite number of non-zero decimal digits. For example, 3.125 is a terminating decimal.
Repeating Decimal: ↑ A decimal expansion where the digits repeat. That is, eventually the digits fall into a pattern that repeats forever. For example, 0.3333… and 3.125353535… are repeating decimals.
Irrational Number: ↑ A real number that cannot be written as a fraction of two integers . Decimal expansions for irrational numbers are infinite decimals that do not repeat.
Dense: ↑ A set of numbers is dense in the real numbers if for any two different real numbers, there is a number from the set in between them. For example, the integers are not dense in the real numbers because there is no integer between 2.1 and 2.2.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
