ملخص
تقول الأسطورة إن أول شخص في اليونان القديمة اكتشف أن هناك أعدادًا لا يمكن كتابتها بصيغة كسور تم التخلص منه من خلال إلقاؤه من إحدى السفن. وبعد مرور عدة قرون، بينما نستخدم - بشكل منتظم - أعدادًا لا يمكن كتابتها بصيغة كسور، تظل هذه الأعداد التي يمكن كتابتها في صيغة كسور أدوات قوية في الرياضيات. ما الذي يجعل الكسور مميزة للغاية؟ سنستكشف كيف يمكننا التعرف على التمثيل العشري للكسور وكيف يمكن استخدام الكسور لتقريب أي عدد حقيقي بقدر ما نرغب.
في صباح يوم اثنين، يمشي معك صديقك أحمد ويقول: "أفكر في عدد يقع بين 1 و100". بدت لك هذه رياضة ممتعة، لذا بدأت في اللعب وخمنت عدد 43. قال أحمد: "لا، هذا عدد منخفض للغاية!" ثم سألت: "حسنًا، ما رأيك بعدد 82؟" أجاب أحمد: "عدد مرتفع للغاية!" واستمرَرْتُ أنت في التخمين. 60 عدد منخفض للغاية. 76 عدد مرتفع للغاية. 70 عدد منخفض للغاية. ثم شعرت بالحماس لأنك أوشكت على الوصول إلى الإجابة، ثم سألت: "ما رأيك بعدد 75؟" أجاب أحمد: "لقد وصلت إلى الإجابة الصحيحة"، وأنت شعرت بالسعادة والانتصار واتجهت نحو صفك الأول في اليوم.
لكن بعد انتهاء الصف، التقيت مجددًا بأحمد، الذي كان يبدو عليه أن يفكر في طرق لإرباكك: لما تتقيد بالأعداد الموجبة؟
ماذا لو أفسحت المجال للأعداد السالبة؟ يقول أحمد ببهجة: "الآن أفكر في عدد يقع بين سالب 100 و100". لقد قررت أن تبتلع الطعم، وسريعًا ما تكتشف أن هذا لا يغير من اللعبة كثيرًا. تستمر في التخمين، ومع تخمين أعداد أقل أو أكبر، تقترب أكثر من الوصول إلى الإجابة الصحيحة. إذا كان العدد الذي يقصده أحمد -32، وأدركت بالفعل أن العدد -33 منخفض للغاية والعدد -31 مرتفع للغاية، فستدرك حينئذ أن الإجابة هي -32. ولكنك تدرك بعد ذلك: لا يوجد شيء مميز في اختيار النطاق من ١٠٠ إلى فإذا بدأت بعدد يتراوح بين 1000 و-1000، فستعلم أنك ستخمن العدد الصحيح في النهاية حتى لو تطلب الأمر إجراء عدد أكبر من التخمينات. ثم تذهب الآن إلى صفك الثاني منتصرًا، وعلى ثقة بأنك على أتم استعداد لتحدي أحمد التالي.
ومع ذلك، تدرك في أثناء الصف أنك كنت تفترض أن أحمد يختار دائمًا عددًا صحيحًا. ماذا سيحدث إذا أُفسح المجال للكسور؟ لنفترض أن أحمد يختار عددًا بين 0 و1، على سبيل المثال . عليك أن تخمن عددًا يقع في مكان على طول خط الأعداد من 0 إلى 1. تحاول البدء بالضبط في المنتصف وتخمين ، ثم يخبرك أحمد أن تخمينك مرتفع، لذلك ستعرف أن إجابتك تقع في خط الأعداد بين 0 و، سيكون تخمينك في المنتصف مرة أخرى: . ويقول أحمد إن ما يزال مرتفعًا، لذلك ستعرف أن الإجابة يجب أن تقع في خط الأعداد بين 0 و. بالاستمرار في اتباع هذا النهج، ستخمن ، ، ، ، يوضح الشكل 1 أحد التصورات لهذه اللعبة. يبدو أن الأمر يستغرق وقتًا طويلًا! هل ستخمن العدد الصحيح؟ ربما سيكون مفيدًا لك تغيير النهج الذي تتبعه. أم هل محكوم عليك بالتخمين إلى الأبد؟
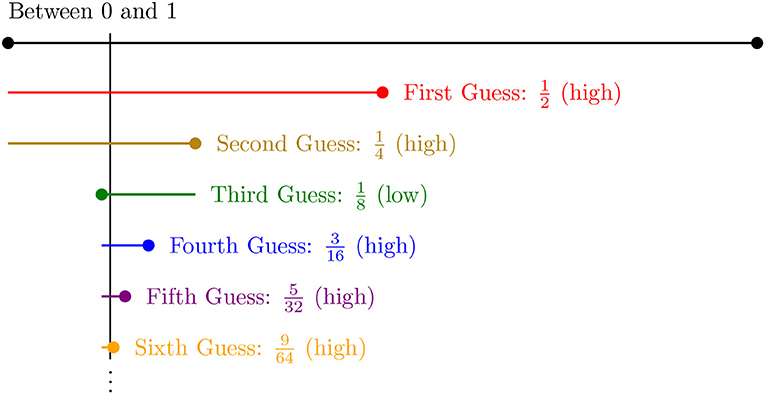
- شكل 1 - هو لعبة لتخمين العدد.
- يطلب منك صديقك أحمد تخمين عدد بين 0 و1. مع كل تخمين، يمكنك تخفيض نطاق التخمين إلى النصف حيث يمكن أن يقع العدد الذي يقصده أحمد. تشير النقطة الموجودة في طرف كل خط إلى تخمينك، ويتميز مكان العدد الذي تحاول تخمينه، ، بخط عمودي أسود اللون.
نهج جديد: المفكوكات العشرية
دعونا ننظر إلى هذه الأعداد بطريقة مختلفة ونفكر فيها باعتبارها كسورًا عشرية بدلًا من ذلك. يمكنك تحويل الكسر إلى رقم عشري عن طريق قسمة البسط على المقام. فيما يلي كيفية إجراء ذلك مع الكسر :
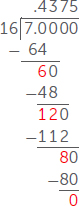
بالنسبة للخطوة الأولى من القسمة، نسأل عن عدد مرات تكرار الرقم 16 في العدد 70. (نحن في الواقع نسأل عن عدد مرات تكرار 1.6 في 7.0، لكن هذا يعادل سؤال عدد مرات تكرار 16 في 70). ولأن 16x 4 = 64، فنكتب 4 أعلى 0 في 7.0. ثم نطرح 64 من 70 ونحصل على 6 المتبقية. في هذه الحالة، تُسمي 6 باقي القسمة.
في الخطوة التالية، نضيف الـ ٠ التالي من 7.00. ثم نسأل عن عدد مرات تكرار 16 في 60. ولأن 16x 3 = 48، فنكتب 3 أعلى الـ ٠ الثاني. وبعد ذلك، نطرح 48 من 60 لنحصل على باقي القسمة 12.
سنواصل هذه العملية من خلال إضافة الأصفار بعد كل باقي قسمة ونسأل ما عدد مرات 16 في العدد الناتج. بعد إجراء هذه العملية أربع مرات، سنحصل على باقي قسمة 0، التي لا تحتوي على 16 فيها. عند هذه المرحلة، ننتهي من القسمة المطولة ونستطيع القول إن = 0.4375. إذا كنت تلعب لعبة تخمين العدد، فستتوصل إلى الصيغة العشرية من 7⁄16 من خلال عدة خطوات بسيطة. يوضح الجدول أدناه الطريقة المحتملة لإجراء ذلك. في هذا الجدول، يشير مرتفع (ويُرمز له بالحرف H) إلى أن التخمين مرتفع للغاية ويشير منخفض (ويُرمز له بالحرف L) إلى أن التخمين منخفض للغاية.

بسبب انتهاء العدد العشري لكسر ، يمكنك الحصول على العدد المضبوط من خلال تخمين رقم واحد كل مرة في الصيغة العشرية. هل تحدث هذه العملية لجميع الكسور؟ دعنا ندرس الصيغة العشرية للكسر .
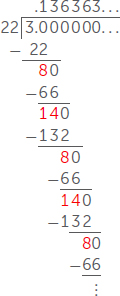
بعد عملية القسمة نفسها، نحصل على 1 في الأعلى مع باقي قسمة 8، و3 في الأعلى مع باقي قسمة 6، و14 في الأعلى مع باقي قسمة 3، و8 في الأعلى مع باقي قسمة ١٤.... لكن انتظر! لقد رأينا بالفعل بواقي القسمة هذه، ونعرف أن العدد التالي في الأعلى هو 6 مع باقي القسمة 14 مرة أخرى. بينما نستمر في عملية القسمة، يعطينا باقيان القسمة المتكرران 8 و14 العددين 3 و6 المتكررين في المفكوك العشري للكسر ، هذا يعني أنه لو أنك تحاول تخمين العدد بخانة عشرية واحدة في المرة، ستظل تخمن للأبد!
الأعداد الكسرية
جميع الأعداد التي درسناها حتى الآن تُسمي الأعداد الكسرية. العدد الكسري هو أي عدد يمكننا كتابته في صيغة كسر س⁄ص من عددين صحيحين (الأعداد الصحيحة وأشكالها السالبة)، س و ص. هذا يعني أن العدد هو عدد كسري لأن كل من الرقمين 2 و5 أعداد صحيحة. كما أن 3 عدد كسري لأن يمكن كتابته في صورة 3 = و 4.5 عدد كسري أيضًا؛ لأنه يمكن كتابته في صورة 4.5 = . حتى لو لم نكن نكتب 3 و 4.5 في صيغة كسور، فهما عددان كسريان لأنه يمكن كتابتهما في صورة كسر يساوي كلًا منهما.
لقد عرفنا أن بعض الأعداد الكسرية، مثل ، لها مفكوكات عشرية لها نهاية، ونطلق على هذه الأعداد اسم الكسور العشرية المنتهية. بينما الأعداد الكسرية الأخرى، مثل ، فلها مفكوكات عشرية غير منتهية، لكننا نعلم أن حتى المفكوكات العشرية التي لا تنتهي فهي تتكرر، لذلك نطلق عليها اسم الكسور العشرية المتكررة.
بالنسبة لأي عدد كسري س⁄ص بواقي القسمة الوحيدة التي يمكننا الحصول عليها عندما نحسب الكسر العشري هي الأعداد 0، 1، 2، 3..... ص - 2، ص - 1. على سبيل المثال، عندما كنا نغير إلى كسر عشري، كانت الاختيارات الوحيدة التي نتوصل إليها في بواقي القسمة هي: 0، 1، 2، 3، ..... 20، 21. لأن هناك عدد متناهي من بواقي القسمة، يجب أن تتكرر بواقي القسمة في نهاية الأمر. وهذا ينطبق على جميع الكسور التي لا تنتهي أعدادها العشرية. على الرغم من وجود نمط متكرر لهذه الأعداد العشرية في هذه الكسور، فإننا لن نخمن العدد الصحيح في لعبة التخمين إذا كنا نخمن خانة عشرية واحدة في كل مرة لأن الأعداد العشرية تمتد إلى ما لا نهاية. لا يمكننا أن نقول أرقامًا كثيرة غير متناهية!
ويمكننا أيضًا أن نغير اتجاهنا بتحويل الكسور العشرية إلى كسور عادية، فإذا كان لدينا مفكوك عشري منتهي مثل الرقم 4.132، فيمكننا تحويله إلى كسر عادي باستخدام مرتبة العدد، وبما أن الرقم 2 في 4.132 موجود في خانة الآلاف، يتحول الرقم من 4.132 إلى وإذا كنا سنحول كسرًا عشريًا متكررًا، فعلينا العمل عليه قليلًا لإيجاد الكسر العادي المقابل له، على سبيل المثال، العدد 0.353535. .. ولنطلق على هذا العدد رمز أ، وحيث إن الجزء المكرر 35 يتكون من رقمين، لذا نضرب أ في 100 لتحريك الكسر العشري خانتين، مما يجعل 100أ = 35.353535 لاحظ أن جميع الخانات العشرية في أ و 100 أ متطابقة. وعلى النحو الموضح، نطرح أ من 100 أ للحصول على رقم 99 أ، وعندما نطرح الكسور العشرية، يصبح العدد 0.353535.. نفسه في العددين ويتم حذفه في الفرق، وبالتالي لن يتبقى لنا سوى الأعداد الصحيحة.
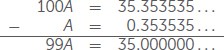
وإذا كانت 99 أ = 35، فهنا عندما نقسم العدد على 99، تصبح لدينا أ = . ويمكننا استخدام نفس العملية للحصول على الكسر المقابل لأي كسر عشري مكرر، وذلك بالضرب في 10 أو 100 أو 1000 أو أي عدد لازم لتحريك العلامة العشرية ما يكفي بحيث تصطف الأرقام العشرية، ثم نطرح ونستخدم الناتج للحصول على الكسر المقابل، وهذا يعني أن كل كسر عشري متكرر هو عبارة عن عدد كسري.
الأعداد غير الكسرية
ماذا إذا كان لدينا مفكوك عشري غير منتهي لكن ذا أعداد غير مكررة؟ على سبيل المثال، انظر إلى العدد 0.101001000100001 . . .. في هذا العدد نزيد عدد الأصفار بين كل زوج من الرقم 1، ليصبح لدينا أولًا 0 بين الزوج الأول من الرقم 1 ثم صفرين ثم ثلاثة أصفار، إلى آخره، ولا يمكن أن يكون هذا عددًا كسريًا نظرًا لأننا نعرف أن الكسور العشرية للأعداد الكسرية إما منتهية أو متكررة، وهذا مثال على الأعداد غير الكسرية. والعدد غير الكسري هو عدد حقيقي لا يمكن كتابته في خط الأعداد ولا يمكن كتابته في صيغة كسر عادي للأعداد الصحيحة، وربما سمعت عن العدد غير الكسري المشهور π = 3.14159 . . .،
والذي يحدد نسبة محيط الدائرة إلى قطرها. وبالرغم من كونه نسبة، فإن قيمة على الأقل؛ من بين محيط الدائرة وقطرها، ليست عددًا صحيحًا، ولذلك فإن π ليست عددًا كسريًا. وهناك عدد كسري آخر وهو 2√ = 1.41421. . .، وهو طول قطر مربع طول ضلعه 1.
وبالعودة إلى لعبتنا، فإن كل الأعداد الكسرية وغير الكسرية تملأ خط الاعداد الخاص بنا من 0 إلى 1. افترض أن صديقك أحمد يمكنه أن يختار أي عدد من بين 0 و1 ثم اختار عددًا غير كسري لتخمنه أنت، فمن المرجح أن تواجه صعوبة في تخمين الرقم بشكل صحيح. فكما هو الحال في المفكوك العشري المتكرر بالعدد ، فلا يمكنك قول عدد غير نهائي من الأرقام ، لذلك ستكون هذه اللعبة غير عادلة.
ولهذا دعنا نغير اللعبة لتتمكن من الفوز. قام أحمد بتحديد ثلاثة أمور: رقم لتخمنه ومجموعة من الأرقام يقع فيها هذا الرقم ونطاق تخمينك من الصواب، وبالقواعد الجديدة للعبة، سيختار أحمد العدد π وسيقول لك: "أنا أفكر برقم بين 2 و10، فلنرَ إذا كان بإمكانك التخمين في نطاق 0.01 من رقمي". وفي هذه الحالة يمكن أن تسير اللعبة بهذا الشكل:

وفي هذه النسخة الجديدة من اللعبة، وحتى إذا غيّر أحمد نطاق تخمينك، فيمكنك دائمًا الوصول إلى تخمين رقم قريب منπ، فكل ما تحتاجه هو معرفة العدد الصحيح وعدد معين من الخانات العشرية بشكل صحيح، على سبيل المثال، لتكون في نطاق 0.1 من π لا تحتاج إلا أن تعرف الخانة العشرية الأولى بشكلٍ صائب. ولكي تكون في نطاق 0.01 من π لا تحتاج سوى أن تعرف أول خانتين عشريتين بشكلٍ صائب. ولتكون في نطاق 0.001 من π، عليك أن تعرف أول ثلاث خانات عشرية صحيحة. وبغض النظر عن مدى قرب تخمينك من الصواب، بإمكانك الفوز في هذه اللعبة الجديدة عن طريق تخمين خانة عشرية كل مرة حتى تحصل على خانات عشرية كافية.
وكما شاهدنا سابقًا أن كل كسر عشري منتهي هو عدد كسري، وإذا اقتربنا أكثر فأكثر من عدد غير كسري من خلال تخمين المزيد من الخانات العشرية للعدد، فسنتمكن من معرفة عدد كسري قريب للعدد غير الكسري المستهدف. وهذا يعني في لعبتنا أنه وبغض النظر عن العدد غير الكسري الذي يختاره أحمد أو قرب تخمينك من الصواب، يمكنك دائمًا العثور على عدد كسري يلبي المتطلبات. ففي هذه اللعبة أنت دائمًا الفائز.
الخلاصة
السبب وراء حدوث ذلك هو كثافة الأعداد الكسرية داخل الأعداد الحقيقية، مما يعني أنه يمكننا دائمًا أن نجد عدد كسري بين أي عددين حقيقيين مختلفين، ولأن الأرقام الحقيقية لها هذه الخاصية، فيمكننا تقريب أي عدد غير كسري بعدد كسري، وتقريب عدد غير كسري بعدد كسري هو ما تفعله في اللعبة الجديدة عندما يختار أحمد عددًا غير كسري.
ولكن لماذا قد تحتاج إلى تقريب عدد غير كسري بعدد كسري؟ افترض انك تبني إطارًا خشبيًا لحوض زرع مثلث على شكل نصف مربع كما في الشكل 2، فستحتاج إلى قطع قطعة خشبية طولها π√2 قدم، فكيف ستقيس هذا الطول؟ ولأن π√2 هو عدد غير كسري، فلا يمكنك قياس الطول بدقة باستخدام شريط القياس. عوضًا عن ذلك ستحتاج إلى اختيار عدد كسري يقارب π√2، ويمكنك استخدام عدد من الأرقام العشرية لتضمينه في المفكوك الخاص بك من أجل تقريب طول القطعة الخشبية إلى π√2، بنفس طريقة اختيارك للأعداد الكسرية لتصبح قريبًا من رقم أحمد في اللعبة.
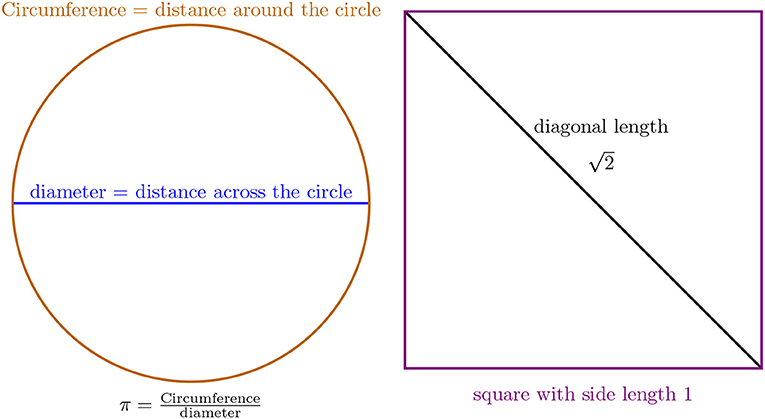
- شكل 2 - عددان غير كسريين نجدهما في الهندسة الرياضية.
إن التقريب باستخدام الأعداد الكسرية يعتبر أداة قوية للقيام بالعمليات الحسابية اللازمة لحساب المواد عند البناء وفي العديد من التطبيقات الأخرى، كما أن حقيقة أن الأعداد الكسرية تعتبر أعدادًا كثيفة داخل الأعداد الحقيقية هو ما جعلنا نستخدم تلك الأداة.
مسرد للمصطلحات
العدد الكسري (Rational numbers): ↑ هو عدد حقيقي لا يمكن كتابته بصيغة كسر عادي مكون من عددين صحيحين س⁄ص، وتكون المفكوكات العشرية للأعداد غير الكسرية كسورًا عشرية غير منتهية وغير مكررة.
الكسور العشرية المنتهية (Terminating decimals): ↑ هي مفكوك عشري لا يحتوي إلا على عدد متناهي من الأعداد العشرية غير الصفرية. على سبيل المثال، 3.125 هو كسر عشري منتهي.
الكسور العشرية المتكررة (Repeating decimals): ↑ هي مفكوك عشري تتكرر فيه الأرقام. أي أن الأرقام تقع في النهاية بنمط يتكرر لا نهاية له. على سبيل المثال، 0.3333 ... و3.125353535 ... هي أعداد عشرية متكررة.
العدد غير الكسري: ↑ هو عدد حقيقي لا يمكن كتابته بصيغة كسر عادي مكون من عددين صحيحين س⁄ص، وتكون المفكوكات العشرية للأعداد غير الكسرية كسورًا عشرية غير منتهية وغير مكررة.
المجموعة الكثيفة: ↑ هي مجموعة من الأعداد الكثيفة داخل الأعداد الحقيقية، بحيث إذا كان هناك عددان حقيقيان مختلفان، فهناك رقم من المجموعة بينهما. على سبيل المثال، الأعداد الصحيحة ليست كثيفة داخل الأعداد الحقيقية لأنه لا يوجد عدد صحيح بين العددين 2.1 و2.2.
إقرار تضارب المصالح
يعلن المؤلفون أن البحث قد أُجري في غياب أي علاقات تجارية أو مالية يمكن تفسيرها على أنها تضارب محتمل في المصالح.
